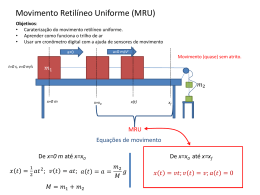
Movimento Retilíneo Uniforme (MRU)
Objetivos:
• Caraterização do movimento retilíneo uniforme.
• Aprender como funciona o trilho de ar
• Usar um cronômetro digital com a ajuda de sensores de movimento
a=0 m/s2
a≠0
t=0 s, v=0 m/s
Movimento (quase) sem atrito.
𝑚1
𝑚2
x=0 m
x(t)
x=x0
xf
MRU
Equações de movimento
De x=0 m até x=x0
1
𝑥 𝑡 = 2 𝑎𝑡 2 ; 𝑣 𝑡 = 𝑎𝑡; 𝑎 𝑡 = 𝑎 =
𝑀 = 𝑚1 + 𝑚2
De x=x0 até x=xf
𝑚2
𝑔
𝑀
𝑥 𝑡 = 𝑣𝑡; 𝑣 𝑡 = 𝑣; 𝑎 𝑡 = 0
Montagem experimental
Aparelhos:
• Trilho de ar: buraquinhos permitem a saída de ar que vem de um compressor. O objetivo é diminuir o atrito
do trilho e o carrinho. Não deixe o carrinho bater na outra extremidade do trilho!
• Disparador: Imã que segura o carrinho. Puxe para soltar.
• Compressor de ar: só ligar o botão atrás, sem mexer no seletor.
• Sensores de movimento: Eles iniciam e param o cronômetro digital
• Cronômetro digital: ligar no botão da parte de trás e usar o botão de RESET para zerar novamente. Não
mude os outros seletores.
• Polia, barbante, porta-peso e pesos.
Cronômetro digital
3
2
1
4
Medidas e Relatório
Procedimento:
1. Revise a montagem e compare com as fotos da apostila. Determine a posição inicial, x0, a partir da qual o
carrinho está em MRU. Anote o valor desta posição a partir do x=0 m.
2. Posicione um dos sensores de movimento nessa posição.
3. Posicione o outro sensor afastado uma certa distância (ex. 0,1 m). Meça o tempo que o carrinho leva para
percorrer essa distância (ti). Repita três vezes.
4. Defina uma nova distância maior. Meça de novo o tempo total que o carrinho demora para percorrer a nova
distância.
5. Repita para, no mínimo, sete distancias.
Análise Obrigatório:
1. Reporte suas medidas na tabela. Os números 1 ao 9 referem-se a DISTANCIAS diferentes.
2. Faça um gráfico de d como função do tempo médio. Não esqueça das barras de erro!
3. Comprove que as variáveis no gráfico seguem uma relação linear.
4. Calcule o coeficiente linear e angular, usando o método gráfico.
5. Compare a equação da reta com a teoria e reporte a velocidade do carrinho no MRU
6. Calcule o valor teórico da velocidade, considerando o movimento com aceleração constante entre x=0 m e
x0.