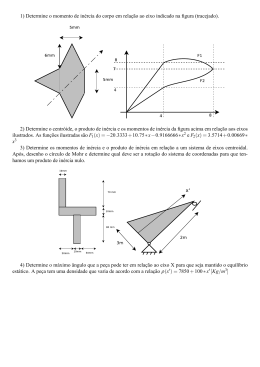
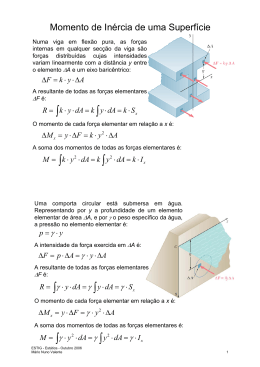
FTC - FACULDADE DE TECNOLOGIA E CIÊNCIAS
RESISTÊNCIA DOS MATERIAIS II
NOTA DE AULA 1
REVISÃO DE MECÂNICA
Profª. Sandra Cunha Gonçalves
ITABUNA-BA, 2011
PRINCÍPIOS BÁSICOS DA MECÂNICA
A Mecânica é uma ciência física aplicada que trata dos estudos das
forças e dos movimentos. A Mecânica descreve e prediz as condições de
repouso ou movimento de corpos sob a ação de forças. A finalidade da
Mecânica é explicar e prever fenômenos físicos, fornecendo, assim, os
fundamentos para as aplicações da Engenharia.
Os conceitos fundamentais da Mecânica baseiam-se na Mecânica Newtonia:
1. Espaço: o conceito de espaço é associado à noção de posição de um ponto
material, o qual pode ser definido por três comprimentos, medidos a partir
de um certo ponto de referência, ou de origem, segundo três direções
dadas. Estes comprimentos são conhecidos como as coordenadas do
ponto;
2. Tempo: para se definir um evento não é suficiente definir sua posição no
espaço. O tempo ou instante em que o evento ocorre também deve ser
dado;
3. Força: a força representa a ação de um corpo sobre outro; é a causa que
tende a produzir movimento ou a modificá-lo. A força é caracterizada pelo
seu ponto de aplicação, sua intensidade, direção e sentido; uma força é
representada por um vetor;
1. Sistema Internacional de Unidades
O Sistema Internacional de Unidades (SI) é subdividido em unidades
básicas e unidades derivadas.
As unidades básicas são: metro (m), quilograma (kg) e segundo (s).
As unidades derivadas são: dentre outras, força, trabalho, pressão, etc...
As unidades do SI formam um sistema absoluto de unidades. Isto
significa que as três unidades básicas escolhidas são independentes dos locais
onde são feitas as medições.


Força é medida em Newton (N), que a partir da Equação F=m.a (segunda
Lei de Newton), escreve-se: 1 N = 1 kg × 1 m/s².
Pressão é medida no SI em Pascal (Pa) que é definido como a pressão
exercida por uma força de 1 Newton uniformemente distribuída sobre uma
superfície plana de 1 metro quadrado de área, perpendicular à direção da
força (Pa = N /m²). Pascal é também unidade de tensões normais
(compressão ou tração) ou tensões tangenciais (cisalhamento).
Múltiplos e submúltiplos
Conversão de Unidades
2. Alfabeto Grego
Os problemas usuais em engenharia são definidos por formulações
matemáticas, as quais, usualmente, utilizam letras do alfabeto grego. É, pois,
necessário, seu conhecimento para as práticas comuns da Engenharia.
3. Características Geométricas de Figuras Planas
O dimensionamento e a verificação da capacidade resistente de barras,
como de qualquer elemento estrutural dependem de grandezas chamadas
tensões, as quais se distribuem ao longo das seções transversais de um corpo.
Daí vem a necessidade de se conhecer claramente as características ou
propriedades das figuras geométricas que formam essas seções transversais.
As principais propriedades geométricas de figuras planas são:
Área (A)
Momento estático (M)
Centro de gravidade (CG)
Momento de Inércia (I) e Momento polar (J)
Módulo resistente (W)
Raio de giração (i)
3.1. Área (A)
A área de uma figura plana é a superfície limitada pelo seu contorno.
Para contornos complexos, a área pode ser obtida aproximando-se a forma
real pela justaposição de formas geométricas de área conhecida (retângulos,
triângulos, etc).
Unidade de área: [L]2 (unidade de comprimento ao quadrado).
Utilizado em: determinação das tensões normais (tração e compressão) e das
tensões de transversais ou de corte.
3.2. Momento Estático (M)
Analogamente à definição de momento de uma força em relação a um
eixo qualquer, define-se Momento Estático (M) de um elemento de superfície
como o produto da área do elemento pela distância que o separa de um eixo
de referência.
Momento Estático de uma superfície plana é definido como a somatória
de todos os momentos estáticos dos elementos de superfície que formam a
superfície total.
Unidade do momento estático: [L]3 (unidade de comprimento ao cubo).
Utilizado em: determinação das tensões transversais que ocorrem em uma
peça submetida à flexão.
3.3. Centro de Gravidade (CG)
Se um corpo for dividido em partículas mínimas, estas ficam sujeitas à
ação da gravidade, isto é, em todas estas partículas está aplicada uma força
vertical atuando de cima para baixo. A resultante de todas estas forças verticais
e paralelas entre si, constitui o peso do corpo.
Portanto, atração exercida pela Terra sobre um corpo rígido pode ser
representada por uma única força P. Esta força, chamada peso do corpo, é
aplicada no seu baricentro, ou cento de gravidade (CG). O centro de gravidade
pode localizar-se dentro ou fora da superfície.
Centro de gravidade de algumas figuras planas
Unidade do centro de gravidade: [L] (unidade de comprimento).
Utilizado em: determinação do ponto de atuação da força gravitacional em um
corpo.
3.4. Momento de Inércia (I)
O momento de inércia de uma superfície plana em relação a um eixo de
referência é definido como sendo a integral de área dos produtos dos
elementos de área que compõem a superfície pelas suas respectivas
distâncias ao eixo de referência, elevadas ao quadrado. É uma característica
geométrica importantíssima no dimensionamento dos elementos estruturais,
pois fornece, em valores numéricos, a resistência da peça. Quanto maior for o
momento de inércia da seção transversal de uma peça, maior a sua
resistência.
Propriedade: O momento de inércia total de uma superfície é a somatória dos
momentos de inércia das figuras que a compõe.
Teorema dos eixos paralelos: O momento de inércia de uma superfície
em relação a um eixo qualquer é igual ao momento de inércia em relação ao
eixo que passa pelo seu centro de gravidade, acrescido do produto da área (A)
pelo quadrado da distância que separa os dois eixos.
Unidade do momento de inércia é: [L]4 (unidade de comprimento a quarta
potência).
Utilizado em: determinação das tensões normais a que estão sujeitas as
peças submetidas à flexão.
3.5. Momento de Inércia polar (J)
É chamado momento polar de inércia ao momento de inércia calculado
em relação ao eixo de giração da peça. Chamamos de momento polar devido a
que ao estudarmos a seção esse eixo nos aparece como um ponto.
O momento polar de inércia de uma seção circular cheia é dado por:
J= .d4
32
Sabendo que o diâmetro vale duas vezes o raio (d=2r), podemos reescrever a
equação como:
J= .r4
2
O momento polar de inércia de uma seção circular vazada é dado por:
J= .(raio externo4 – raio interno4)
2
(a) Secão cheia
(b) Seção vazada( raio externo c2 e raio interno c1)
Unidade do momento de inércia Polar é: [L]4 (unidade de comprimento a
quarta potência).
Utilizado em: determinação das tensões de cisalhamento de elementos
submetidos à torção.
3.6. Módulo Resistente (W)
Define-se módulo resistente de uma superfície plana em relação aos
eixos que contém o CG como sendo a razão entre o momento de inércia
relativo ao eixo que passa pelo CG da figura e a distância máxima entre o eixo
e a extremidade da seção estudada.
onde:
ICG = momento de inércia da peça em relação ao CG da figura
x, y = distância entre o eixo do CG da figura e a extremidade da peça.
Unidade do momento estático: [L]3 (unidade de comprimento ao cubo).
Utilizado em: dimensionamento de peças submetidas à flexão.
3.7.
Raio de Giração (i)
Define-se raio de giração como sendo a raiz quadrada da relação entre o
momento de inércia e a área da superfície.
Unidade do raio de giração: [L] ( unidade de comprimento).
Utilizado em: estudo da flambagem.
EXEMPLO PRÁTICO 1
1. A estrutura abaixo representa a seção transversal de uma viga “T”. Para a
figura, determinar:
a)
b)
c)
d)
O centro de gravidade;
O momento de inércia em relação ao eixo x;
O módulo Resistente superior e o inferior;
O raio de giração.
OBS: Todas as medidas estão em centímetros
Resposta:
CG= 4,65 cm
ICG = 101,55 cm4
Wx superior = 43,21 cm3
Wx inferior = 21,84 cm3
ix = 1,98 cm
OBS 1: Lembre-se de um detalhe, o enunciado da questão diz que se trata de
uma viga, as vigas possuem carregamento longitudinal e por isso, na maioria
das vezes, sofrem deformações em torno do eixo X.
OBS 2: Lembre-se que as resultantes das forças e momentos atuam no centro
de gravidade de um corpo.
EXEMPLO PRÁTICO 2
2. Determinar para o tubo circular vazado indicado na figura abaixo o
momento de inércia polar. Que apresenta diâmetro externo de 60 mm e
diâmetro interno de 40 mm.
Resolução:
Considerando :
Raio externo = metade do diâmetro externo = c2 = 60/2 = 30 mm ou 0,03 m
Raio interno = metade do diâmetro interno = c1 = 40/2 = 20 mm ou 0,02m
Temos:
Tabela : Características Geométricas de algumas figuras conhecidas
Referencial Bibliográfico
1. BEER, F.P. e JOHNSTON, JR., E.R. Resistência dos Materiais, 3.º Ed.,
Makron Books, 1995.
2. BEER, F. P., JOHNSTON Jr., R. Mecânica vetorial para engenheiros estática. 5 ed. São Paulo, Makron Books, 2004.
3. GERE, J. M. Mecânica dos Materiais, Editora Thomson Learning.