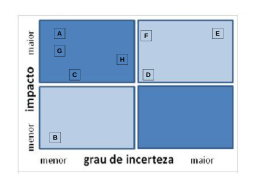
Medidas e Incertezas
• O que é medição?
– É o processo empírico e objetivo de designação de números a propriedades
de objetos ou eventos do mundo real de forma a descreve-los.
– Outra forma de explicar este processo é comparando a quantidade ou
variável desconhecida com um padrão definido para este tipo de
quantidade, implicando então num certo tipo de escala,
CKS
2
1
•
Tipos de medidas
– Medida Nominal
• Quando duas quantidades do mesmo tipo são comparadas para saber se são
iguais (Ex. duas cores , acidez de dois líquidos)
– Medida Ordinal
• Quando é necessário ter informação a tamanhos relativos (Ex. Classificação
por peso e altura de uma turma))
– Medida em Intervalos
• Quando deseja-se uma informação mais especifica, envolve-se então uma
certa escala, sem incluir pontos de referência ou zero. (Ex. no caso anterior
usar a escala de metros e quilogramas)
– Medidas Normalizadas
• Define-se um ponto de referência e realiza-se a razão, dividindo cada medida
pelo valor de referência, determinando as magnitudes relativas. (Ex. O maior
valor obtido será 1, quando foi escolhido como referência o valor máximo
medido).
– Medidas Cardinais
• O ponto de referência é comparado com um padrão definido. Assim todo
parâmetro físico pode ser medido contra uma referência padrão, como o
Sistema Internacional de medidas SI.
CKS
3
CKS
4
2
•
O Processo de Medida
– Operador
• Conhecimento do processo de medida
• Domínio do instrumento de medida
• Escolha adequada do instrumento
– Instrumento de Medida
• Exemplo 1
Objeto a ser medido
Valor medido:
20 ≤ m ≤ 25
A medida é um intervalo e não um número
O intervalo [20:25] é conhecido como:
Intervalo de Confiança
O Intervalo de Confiança é no mínimo igual à precisão do equipamento. Neste caso = 5
CKS
5
•
INCERTEZA DA MEDIDA
Intervalo de Confiança
2
mMax − mMin )
(
δ=
2
25 − 20 )
(
δ =
= 2,5
2
Incerteza = δ =
•
Representação da Medida
mMin = 20
mMax = 25
m = m ±δm
mas
m=
( mMax + mMin ) ± δ m
2
( 25 + 20 ) ± 2,5 = 45 ± 2,5 = 22,5 ± 2,5
m=
2
CKS
2
então
m = 22,5 ± 2,5
6
3
•
Exemplo 2
Objeto a ser medido
Valor medido:
21 ≤ m ≤ 22
δ=
δ=
( mMax − mMin )
2
( 22 − 21) = 1 = 0,5
2
2
CKS
7
•
Representação da Medida
mMin = 21
mMax = 22
m = m ±δm
mas
m=
m=
CKS
( mMax + mMin ) ± δ m
2
( 22 + 21) ± 0,5 = 43 ± 0,5 = 21,5 ± 0,5
2
2
então
m = 21,5 ± 0,5
8
4
– Resumindo
• Medida
– É um Intervalo e não um valor
• Intervalo de Confiança
– Depende do processo de medida (instrumento / operador)
– Intervalo entre o valor Máximo e Mínimo da Medida
» Intervalo de Confiança = [mMax – mMin]
– Seu valor mínimo é igual a precisão da escala do equipamento de medida.
Freqüentemente é maior.
• Incerteza
– Depende o processo de medida
– Seu valor é estimado a partir do intervalo de confiança
– É a metade do intervalo de confiança
• Incerteza Explícita
– 123,05 + 0,01
• Incerteza Implícita (a incerteza esta na primeira casa decimal)
– 123,1
CKS
9
– Conclusão
• Precisão de uma escala → é sua menor divisão
– Ex.: Uma régua com divisão em milímetros
– Sua precisão é 1 mm = Intervalo de Confiança
• Como a incerteza corresponde à (Intervalo de Confiança)/2
– Então a Incerteza de um equipamento é
– Incerteza do Equip. = (Precisão do Equip.) / 2
CKS
10
5
– Incerteza de um Conjunto de Medidas
• Vamos supor um voltímetro com precisão de 1 microvolt
• De saída é possível definir a incerteza do equipamento
– Incerteza = Precisão / 2 = 1µV / 2 = 0,5 µV = 0,0000005 V
• Os valores medidos foram
•
•
•
•
•
Medida
Valor (V)
1
0,126821
2
0,125982
3
0,127003
4
0,125827
5
0,126598
Valor médio do conjunto de dados: 0,126446 V
Desvio padrão do conj. de medidas: 0,0005177921 V
Valor Máximo medido: Max = 0,127003 V
Valor Mínimo medido: Min = 0,125827 V
Representação da Incerteza do Conjunto de Medidas
CKS
11
– Representação
• Opção 1 → A mais correta
– Incerteza = Desvio Padrão + Incerteza do Equipamento
– δ = 0,0005177921 + 0,0000005 = 0,0005182921 V
• Opção 2 → A mais simples (a que nós empregamos)
– Incerteza = (Max – Min)/2 + Incerteza do Equipamento
– δ = 0,000588 + 0,0000005 = 0,0005885 V
CKS
12
6
– Algarismos Significativos
• São todos os algarismos obtidos no processo de medida.
• Os zeros incluidos para localizar o ponto decimal não contam (zeros à esquerda)
• Ex.:
–
–
–
–
–
1945,1
0,00034
1000
2 x 105
4,189 x 10-7
(5 algarismos significativos)
(2 algarismos significativos)
(4 algarismos significativos)
(5 algarismos significativos)
(4 algarismos significativos)
• A Incerteza só deve conter UM (1) algarismo significativo
– LOGO:
» A incerteza deve ser arredondada após sua determinação
CKS
13
– Mudanças de Unidade
• Ao mudar a unidade de uma medida é importante não alterar o número
de algarismos significativos
• Ex.:
– 46 cm → 0,46 m (Está correto)
– 46 cm → 460 mm (está errado pois aumentou a incerteza)
• A notação de potencia de dez evita este problema
– 46 cm → 46 x 101 mm
– Por convenção apenas a mantissa tem algarismos significativos
CKS
14
7
– Critérios de Arredondamento
• O critério de arredondamento a ser utilizado será igual ao empregado por
calculadoras científicas e programas afins.
• Se o número à direita do ponto de arredondamento é:
– 0, 1, 2, 3, 4 → Simplesmente elimina-se a parte a direita
– Ex.: dado o número 0,563729452
» Arredondando para 8 casas depois da vírgula
» = 0,56372945
» Arredondando para 4 casas depois da vírgula
» = 0,5637
» Arredondando para 2 casas depois da vírgula
» = 0,56
– 5, 6, 7, 8, 9 → Incrementa o algarismo à esquerda e elimina a parte à direita.
– Ex.: dado o número 0,563729452
» Arredondando para 7 casas depois da vírgula
» = 0,5637295
» Arredondando para 5 casas depois da vírgula
» = 0,56373
» Arredondando para 1 casa depois da vírgula
» = 0,6
CKS
15
– Usando o Arredondamento para Representar Medidas
• Como a Incerteza de uma medida só deve ter um algarismo significativo então a medida anterior
fica:
• Medida Anterior
• Opção 2 → A mais simples (a que nós empregamos)
– Tensão = 0,126446 + 0,0005885 V
• Ajustando a Incerteza para 1 algarismo significativo
– Tensão = 0,126446 + 0,0006 V
• Para ajustar o valor médio da medida basta ver quantas casas decimais depois da vírgula existem na
incerteza (4 neste caso)
–
–
Logo o valor da medida deve ser ajustado para 4 casas decimais com o arredondamento necessário
Então:
– Tensão = 0,1264 + 0,0006 V (Resultado Final)
– OBSERVAÇÃO MUITO IMPORTANTE
– Os arredondamentos somente devem ser efetuados no final de todas as contas.
– Razão: cada arredondamento intruduz erro (pequeno) mas que ao longo de diversas
contas pode resultar em um número sem significado físico.
CKS
16
8
•
Operações Matemáticas com Medidas
– Sempre que uma operação matemática é efetuada com duas medidas o resultado
deve considerar as incertezas de cada medida a fim de determinar a incerteza do
resultado da operação.
– Existe uma formulação genérica que permite determinar a incerteza em qualquer
operação matemática efetuada com uma ou mais medidas.
– Esta formulação leva em consideração os valores máximo e mínimo da medida.
– Ex.: Supondo duas medidas com suas respectivas incertezas conforme:
• A = a + δa
• B = b + δb
CKS
•
17
Soma das Medidas
A + B = ( a ± δ a ) + ( b ± δ b ) = ( a + b) ±
[ Max − Min ]
2
Maior valor que a operação pode assumir
Max = ( a + δ a ) + ( b + δ b )
Menor valor que a operação pode assumir
Min = ( a − δ a ) + ( b − δ b )
•
Exemplo
A + B = (14, 2 ± 0, 2 ) + ( 5, 3 ± 0,1) = (14, 2 + 5, 3) ±
[ Max − Min ]
2
Maior valor que a operação pode assumir
Max = (14, 2 + 0, 2 ) + ( 5, 3 + 0,1) = 14, 4 + 5, 4 = 19,8
Menor valor que a operação pode assumir
Min = (14, 2 − 0, 2 ) + ( 5,3 − 0,1) = 14, 0 + 5, 2 = 19, 2
A + B = 19,5 ±
CKS
[19,8 − 19, 2] = 19,5 ± 0, 3
2
18
9
•
Subtração das Medidas
A − B = ( a ± δ a ) − ( b ± δ b ) = ( a − b) ±
[ Max − Min ]
2
Maior valor que a operação pode assumir
Max = ( a + δ a ) − ( b − δ b )
(cuidado com os sinais)
Menor valor que a operação pode assumir
Min = ( a − δ a ) − ( b + δ b )
•
(cuidado com os sinais)
Exemplo
A − B = (14, 2 ± 0, 2 ) − ( 5,3 ± 0,1) = (14, 2 − 5, 3) ±
[ Max − Min ]
2
Maior valor que a operação pode assumir
Max = (14, 2 + 0, 2 ) − ( 5,3 − 0,1) = 14, 4 − 5, 2 = 9, 2
Menor valor que a operação pode assumir
Min = (14, 2 − 0, 2 ) − ( 5, 3 + 0,1) = 14,0 − 5, 4 = 8, 6
A − B = 8, 9 ±
[9, 2 − 8, 6] = 8,9 ± 0, 3
2
CKS
•
19
Multiplicação das Medidas
A × B = ( a ± δ a ) × ( b ± δ b ) = ( a × b) ±
[ Max − Min ]
2
Maior valor que a operação pode assumir
Max = ( a + δ a ) × ( b + δ b )
Menor valor que a operação pode assumir
Min = ( a − δ a ) × ( b − δ b )
•
Exemplo
A × B = (14, 2 ± 0, 2 ) × ( 5, 3 ± 0,1) = (14, 2 × 5, 3) ±
[ Max − Min ]
2
Maior valor que a operação pode assumir
Max = (14, 2 + 0, 2 ) × ( 5, 3 + 0,1) = 14, 4 × 5, 4 = 77,76
Menor valor que a operação pode assumir
Min = (14, 2 − 0, 2 ) × ( 5,3 − 0,1) = 14,0 × 5, 2 = 72,8
A − B = 75, 26 ±
CKS
[77, 76 − 72,8] = 75, 26 ± 2, 48 = 75 ± 2
2
20
10
•
Divisão das Medidas
A ( a ± δ a )  a  [ Max − Min ]
=
= ±
B (b ± δ b)  b 
2
Maior valor que a operação pode assumir
Max =
(a + δ a )
(b − δ b)
(cuidado com os sinais)
Menor valor que a operação pode assumir
Min =
•
Exemplo
(a − δ a )
(b + δ b)
(cuidado com os sinais)
A (14, 2 ± 0, 2 )  14, 2  [ Max − Min ]
=
=
±
B
2
( 5, 3 ± 0,1)  5,3 
Maior valor que a operação pode assumir
Max =
(14, 2 + 0, 2 ) = 14, 4 = 2,76923 (apenas as 5 primeiras casas decimais)
( 5,3 − 0,1) 5, 2
Menor valor que a operação pode assumir
Min =
A
[ 2,76923 − 2,59259] = 2,67924 ± 0,08832=2,68 ± 0,09
= 2,67924 ±
B
2
CKS
•
(14, 2 − 0, 2 ) = 14,0 = 2,59259 (apenas as 5 primeiras casas decimais)
( 5, 3 + 0,1) 5, 4
21
Exponenciação de uma Medida
3
B 3 = ( b ± δ b ) = b3 ±
[ Max − Min ]
2
Maior valor que a operação pode assumir
Max = ( b + δ b )
3
Menor valor que a operação pode assumir
•
Exemplo
Min = ( b − δ b )
3
3
3
B 3 = ( 5,3 ± 0,1) = ( 5,3) ±
[ Max − Min ]
2
Maior valor que a operação pode assumir
3
3
Max = ( 5,3 + 0,1) = ( 5, 4 ) = 157,464
Menor valor que a operação pode assumir
3
3
Min = ( 5,3 − 0,1) = ( 5, 2 ) = 140,608
B = 148,877 ±
CKS
[157,464 − 140,608] = 148,877 ± 8,428=149 ± 8
2
22
11
• Erros
– Erros Sistemáticos
• São erros constantes e geralmente conhecidos
• Causas
–
–
–
–
Instrumento
Método
Operador
Outros fatores (climáticos, mecânicos,...)
• Detecção
– Medir com outro equipamento
– Medir empregando outro método
– Medida por outro operador
– Erro Grosseiro
•
•
•
•
Técnica Inadequada
Imperícia do Operador
Ex.: Erro na leitura da escala / digitação
Podem ser completamente eliminados
CKS
23
– Erros Randômicos
• Permanecem após a eliminação dos erros sistemáticos
• Propriedades:
– Erros randômicos positivos e negativos tem a mesma probabilidade de ocorrência.
– São menos prováveis quando o valor absoluto medido aumenta.
– Quando o número de medidas aumenta a média aritmética dos erros randômicos em
uma amostra tende a zero.
– Para um determinado método de medida os erros randômicos não excedem um
determinado valor. Medidas excedendo este valor devem ser refeitas e, se necessário,
estudadas separadamente.
• Erros randômicos também são chamados de Acidentais ou Fortuitos
CKS
24
12
Preciso
Impreciso
Exato
δA
δA
Inexato
δS
δS
δA → Erro Aleatório
δS → Erro Sistemático
CKS
25
FIM
13