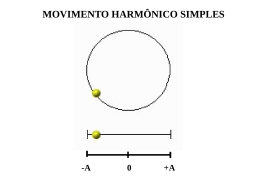
Acústica
Acústica
• Acústica é o estudo das ondas sonoras;
• Ondas sonoras são mecânicas, longitudinais
tridimensionais;
• Ondas sonoras não se propagam no vácuo;
Vibração
Orelha
V

e
Tímpano
Nervo
Fonte oscilando
com freqüência f

Compressão
Rarefação
Cérebro
Acústica – A Freqüência do Som
• Infra-som: sons com freqüências abaixo de 20Hz.
Não perceptível ao ser humano;
• Ultra-som: sons com freqüências acima de 20000Hz.
Não perceptível ao ser humano;
• Som audível: sons com freqüências perceptíveis ao
ser humano (20Hz a 20000Hz)
Infra-som
Som audível
Ultra-som
f (Hz)
0
20
20.000
Acústica – A Velocidade do Som
• As ondas sonoras propagam-se em meios sólidos,
líquidos e gasosos, com velocidades que dependem das
diferentes características dos materiais. De um modo
geral, as velocidades maiores ocorrem nos sólidos e as
menores, nos gases.
• A 20°C, o som propaga-se no ferro sólido a 5100m/s, na
água líquida a 1450m/s e no ar a 343m/s.
VSól .  VLíq .  VGas .
 Densidade  velocidade 
Acústica – A Altura do Som
• qualidade que permite diferenciar um som de alta
freqüência (agudo) de um som de baixa freqüência
(grave). A altura do som depende apenas da
freqüência.
Som alto - Freqüência maior - som agudo
Som baixo - Freqüência menor - som grave
• As notas musicais possuem alturas sonoras
diferentes, isto é, cada nota possui uma freqüência
característica.
Acústica – A Intensidade do Som
• qualidade que permite diferenciar um som forte de
um som fraco. A intensidade do som está relacionada
com energia que a onda transfere e com a amplitude
da onda.
Um som de
maior volume
Uma onda sonora de
maior amplitude.
Maior transporte de
energia pela onda
Som de maior intensidade
Intensidade do Som
• Intensidade física:
I 
E
A  t
E
 P  Potência
t
A = Área
P constante
E = Energia
AI
t = tempo
• Unidade no SI:
J
m2  s
W
m2
P
I 
A
Intensidade do Som
• Mínima intensidade física ou limiar de audibilidade
(Io): é o menor valor da intensidade física ainda audível,
vale:
I o  10 12
W
m2
• Máxima intensidade física ou limiar de dor (Imáx): é
o maior valor da intensidade física suportável pelo
ouvido, vale:
I máx  1
W
m2
Intensidade do Som
• Intensidade auditiva ou nível sonoro (  ):
I
  10  log
Io
• A unidade de nível sonoro, para a
equação dada, é o decibel (dB).
• Um ambiente com:
I o  10
12
2
W m  o  0dB
2
I Máx  1W m  Máx  120dB
40dB é calmo;
60dB é barulhento
mais
de
80dB
já
constitui poluição sonora.
Acústica – O Timbre do Som
• Qualidade que permite diferenciar duas ondas sonoras
de mesma altura e mesma intensidade, emitidos por
fontes distintas.
• O timbre está relacionado à forma da onda emitida pelo
instrumento.
Diapasão
Flauta
Violino
Voz (letra a)
Clarineta
Reflexão do Som
• Persistência acústica : menor intervalo de tempo para
que dois sons não se separem no cérebro. A persistência
acústica do ouvido humano é de 0,1s.
• Um ouvinte consegue distinguir dois sons distintos desde
que os receba em intervalos de tempo maiores (ou
iguais) a 0,1s.
• Esse fato possibilita ao observador perceber o fenômeno
da reflexão do som em três níveis: eco, reverberação e
reforço.
Reflexão do Som
• t=intervalo de tempo para que o som que foi emitido pelo
observador e refletido seja recebido pelo mesmo.
t  0s
t
• Eco: ocorre quando t  0,1s. O observador ouve separadamente o
som direto e o som refletido.
• Reverberação: ocorre quando t < 0,1s. Há um prolongamento
da sensação auditiva.
• Reforço: ocorre quando t  0s. Há somente um aumento da
intensidade sonora.
Freqüências Naturais e Ressonância
• Batendo-se numa das hastes do diapasão, as duas vibram
com determinada freqüência (normalmente, 440Hz). Essa
é a freqüência natural (ou própria) do diapasão.
diapasão
• Todos os corpos possuem uma freqüência própria (prédio,
ponte, copo, etc.).
Exemplo de Ressonância
• A ponte de Tacoma Narrows entrou em ressonância, provocada pela
vibração dos cabos metálicos existentes em sua estrutura. Suas
amplitudes de oscilação aumentaram a ponto de provocar sua ruína
Efeito Doppler
• O efeito Doppler, para ondas sonoras, constitui o
fenômeno pelo qual um observador percebe uma
freqüência diferente daquela emitida por uma fonte,
devido ao movimento relativo entre eles (observador e
fonte).
• É o que acontece quando uma ambulância, com sua
sirene ligada, passa por um observador (parado ou
não). Enquanto a ambulância se aproxima, a
freqüência por ele percebida é maior que a real (mais
aguda); mas, à medida que ela se afasta, a freqüência
percebida é menor (mais grave).
Observador em Repouso e fonte em movimento
• Fonte aproxima-se do observador O1: haverá um encurtamento
aparente do comprimento de onda 1, em relação ao  normal. A
freqüência percebida pelo observador será maior que a freqüência
real da fonte.
• Fonte afasta-se do observador O2, haverá um alongamento aparente
do comprimento de onda 2, em relação ao  normal. A freqüência
percebida pelo observador será menor que a freqüência real da
fonte.
O2
O1
V
F
Observador em Repouso e fonte em movimento
• Para o observador O1, que se aproxima de F, haverá um maior
número de encontros com as frentes de onda, do que se
estivesse parado. A freqüência por ele percebida será maior
que a normal.
• Para o observador O2, que se afasta de F, haverá um menor
número de encontros com as frentes de onda, do que se
estivesse parado. A freqüência por ele percebida será menor
que a normal.
V
V
F
O1
V=0
O2
Efeito Doppler - Conclusão
• Movimento de aproximação entre fonte e observador:
f RECEBIDA  f EMITIDA
• Movimento de afastamento entre fonte e observador:
f RECEBIDA  f EMITIDA
Exercícios
• 2. (PUC-RS) Quanto a sua natureza e forma de
propagação, as ondas podem ser classificadas em
eletromagnéticas ou mecânicas, de longitudinais ou
transversais. Uma das evidências que as ondas sonoras
são longitudinais é que elas não sofrem:
a)
b)
c)
d)
e)
reflexão.
refração.
interferência.
polarização.
difração.
Alternativa D
Exercícios
• 3. (Unirio) Dois operários, A e B, estão parados no pátio
de uma fábrica. Em certo instante, a sirene toca. O
operário B ouve o som da sirene 1,5 s após o operário A
tê-lo ouvido. Considerando a velocidade do som
constante e de módulo 340 m/s, a distância, em metros,
entre os dois operários é:
A
B
Solução - 3
VSom
A
tSom
B
d
t Som  1,5s

Dados VSom  340 m s
d  ?

V Som
d
d

 340 
t Som
1,5
d  510 m
Alternativa C
Exercícios
•
4. (FEI-SP) Quando uma onda sonora atinge uma região
em que a temperatura do ar é diferente altera-se:
a)
b)
c)
d)
e)
a freqüência.
o comprimento de onda.
o timbre.
a intensidade do som.
a altura do som.
f constante
Temperatura varia
Densidade varia
V e  variam
Alternativa B
Exercícios
•
6. (Fatec-SP) Quando uma onda sonora periódica se
propaga do ar para a água:
a)
b)
c)
d)
e)
o comprimento de onda aumenta.
o comprimento de onda diminui.
a freqüência diminui.
f constante
a velocidade diminui.
Densidade aumenta
nda.
V e  aumentam
Alternativa A
Exercícios
•
a)
b)
c)
d)
e)
7. Uma pessoa em P1 emite um som que alcança o
ouvido de outra pessoa, situada em P2, no fundo do mar.
Qual dos caminhos mostrados na figura deste problema
poderia representar a trajetória seguida pela onda
sonora de P1 até P2?
P1AP2.
f constante
P1BP2.
Densidade aumenta
P1CP2.
V e  aumentam
P1DP2.
Ângulo aumenta
P1EP2.
Afasta da normal
Alternativa D
Exercícios
•
a)
b)
c)
d)
e)
8. (Fafeod-MG) Uma pessoa, a 680m de distância de um
obstáculo refletor, dá um grito e ouve o eco de sua voz.
A velocidade do som no ar é de 340m/s. O tempo gasto
entre a emissão do som e o momento em que a pessoa
ouve o eco, em segundos, é igual a:
um valor que não pode ser calculado com os dados
fornecidos.
1
Distância percorrida pelo som d= 2680= 1360m
2
Velocidade do som = 340m/s
4
8
d
1360
Alternativa D
V 
t
 t 
340
 t  4s
Exercícios
•
9. (UFU-MG) Um estudante de Física se encontra a uma
certa distância de uma parede, de onde ouve o eco de
suas palmas. Desejando calcular a que distância se
encontra da parede, ele ajusta o ritmo de suas palmas
até deixar de ouvir o eco, pois este chega ao mesmo
tempo que ele bate as mãos. Se o ritmo das palmas é
de 30 palmas por minuto e a velocidade do som é de
aproximadamente 330m/s, a sua distância da parede é
de:
Freqüência das palmas f=30 palmas/min
Velocidade do som = 330m/s
Intervalo de tempo entres as palmas (T) = tempo de eco (t)
Exercícios – Solução 9
Freqüência das palmas f=30 palmas/min
Velocidade do som = 330m/s
Intervalo de tempo entres as palmas (T) = tempo de eco (t)
f 
30 palmas
30 palmas
1

 f  palmas s
1 min
60 s
2
1
1
T  
 T  2s
f
12
T  t  t IDA  tVOLTA  t IDA  1s
d
d
V 
 330 
t IDA
1
d  330 m Alternativa C