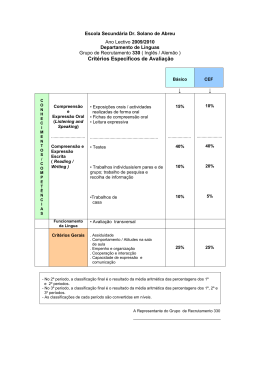
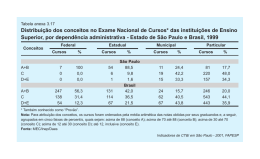
Prof. M. Sc. Jarbas Thaunahy Santos de Almeida
1
Aula 9
Estimativa do intervalo de
confiança
2
Roteiro
Introdução
Estimativa do Intervalo de Confiança da Média Aritmética
3
Introdução
Ao estudar o Teorema do Limite Central e o conhecimento sobre a
distribuição da população para determinação do percentual de médias
aritméticas de amostras que estão dentro dos limites de certas distâncias
da média aritmética da população, utiliza-se o raciocínio dedutivo.
Uma vez que as conclusões são baseadas do geral (população) para o
específico (média aritmética da amostra).
O intervalo de confiança utiliza o método indutivo. Esse método permite
utilizar algumas especificidades no intuito de realizar generalizações mais
abrangentes.
4
Introdução
Não é possível assegurar que as
generalizações mais abrangentes sejam
absolutamente corretas, mas com uma
escolha criteriosa das especificidades e uma
rigorosa metodologia, pode-se chegar a
conclusões bastante úteis.
5
Introdução
Uma estimativa de ponto é o valor de uma única
estatística da amostra.
Uma estimativa de intervalo de confiança
corresponde a uma extensão de valores, conhecida
como intervalo, construída em torno da estimativa
de ponto.
6
Estimativa do intervalo de confiança
da média aritmética
No caso do exemplo que tratou do abastecimento de caixas
de cereais, estimamos a média aritmética da população
utilizando informações oriundas de uma única amostra.
Por conseguinte, em vez de tomar   (1,96)(/n) para
encontrar os limites superior e inferior em torno de ,
substituímos  desconhecido pela média aritmética da
amostra, X, e utilizamos X  (1,96)(/n) como um
intervalo para estimar  desconhecido.
7
Estimativa do intervalo de confiança
da média aritmética
No caso dos cereais, encontre um intervalo
simetricamente distribuído em torno da média aritmética
da população que inclua 95% das médias aritméticas das
amostras, tendo como base amostras com 25 caixas.
Se 95% das médias aritméticas de amostras estão contidas no
intervalo, então 5% estão fora do intervalo. Dividindo os 5% em
duas partes iguais, temos 2,5%. O valor de Z, na Tabela da
distribuição normal padronizada acumulada, corresponde a
uma área aproximada de 0,025 na cauda inferior da curva
normal, é -1,96, e o valor de Z correspondente a uma área
acumulada de 0,975 (aproximadamente) é +1,96.
8
Estimativa do intervalo de confiança
da média aritmética
X Inferior
15
 368  (1,96)
 362,12
25
X Superior
15
 368  (1,96)
 373,88
25
Por conseguinte, 95% de todas as médias aritméticas
de amostras, baseadas nas amostras de 25 caixas,
estarão entre 362,12 e 373,88 gramas.
9
Estimativa do intervalo de confiança
da média aritmética
Suponha que uma amostra de tamanho n = 25 caixas tenha uma
média aritmética de 362,3 gramas.
O intervalo desenvolvido para estimar  é igual a
362,3  (1,96) (15/25)
ou
362,3  5,88
A estimativa de  é: 356,42    368,18
A média aritmética da população () está incluída nos limites do intervalo!
10
Estimativa do intervalo de confiança
da média aritmética
Para dar continuidade, suponha que, para uma amostra
diferente de n = 25 caixas, a média aritmética é 369,5 gramas.
O intervalo desenvolvido para estimar  é igual a
369,5  (1,96) (15/25)
ou
369,5  5,88
A estimativa de  é: 363,62    375,38
A média aritmética da população () está incluída nos limites do intervalo!
11
Estimativa do intervalo de confiança
da média aritmética
Uma terceira amostra hipotética de tamanho n = 25 caixas, seja
selecionada e que a média aritmética dessa amostra seja igual a
360 gramas.
O intervalo desenvolvido para estimar  é igual a
360  (1,96) (15/25)
ou
360  5,88
A estimativa de  é: 354,12    365,88
A média aritmética da população () não está incluída nos limites do intervalo!
12
Estimativa do intervalo de confiança
da média aritmética
Vejamos mais duas amostras hipotéticas, uma amostra com a
média aritmética igual a 362,12 gramas e a outra com 373,88
gramas.
O intervalo desenvolvido para estimar  da primeira é
igual a
362,12  (1,96) (15/25)
ou
362,12  5,88
A estimativa de  é: 356,24    368,00
A média aritmética da população () se encontra no limite superior do
intervalo!
13
Estimativa do intervalo de confiança
da média aritmética
Vejamos mais duas amostras hipotéticas, uma amostra com a
média aritmética igual a 362,12 gramas e a outra com 373,88
gramas.
O intervalo desenvolvido para estimar  da segunda é
igual a
373,88  (1,96) (15/25)
ou
373,88  5,88
A estimativa de  é: 368,00    379,76
A média aritmética da população () se encontra no limite inferior do
intervalo!
14
Estimativa do intervalo de confiança
da média aritmética
15
Estimativa do intervalo de confiança
da média aritmética
CONCLUSÃO
INTERVALO DE CONFIANÇA DE 95%
“Estou 95% confiante de que a média aritmética da quantidade
de cereal na população de caixas está posicionada em algum
lugar entre 362,12 e 373,88 gramas”
16
Estimativa do intervalo de confiança
da média aritmética
INTERVALO DE CONFIANÇA PARA A MÉDIA ARITMÉTICA
( CONHECIDO)
X  Z
X  Z

2
n

2
n
   X  Z

2
n
17
Estimativa do intervalo de confiança
da média aritmética
O valor de Z/2 necessário para construir um intervalo de
confiança é chamado de valor crítico para a distribuição.
95% de confiança, correspondem a um valor de  igual 0,005.
O valor crítico de Z, correspondente a uma área acumulada de
0,975, é igual a 1,96, uma vez que existe 0,025 na cauda superior
da distribuição e a área acumulada que corresponde a menos do
que Z = 1,96 é 0,975.
18
Estimativa do intervalo de confiança
da média aritmética
Um fabricante de papel utiliza um processo de produção que opera
continuamente ao longo de todo um turno de produção. Espera-se que o
papel apresente uma média aritmética de comprimento igual a 11 polegadas
e que o desvio-padrão do comprimento seja igual a 0,02 polegada. Em
intervalos periódicos, são selecionadas amostras para determinar se a média
aritmética do comprimento do papel permanece, ainda, igual a 11 polegadas
ou se no processo de produção ocorreu algo de errado que possa ter
modificado o comprimento do papel produzido. Você seleciona uma amostra
aleatória com 100 folhas, e a média aritmética do comprimento do papel é
igual a 10,998 polegadas. Construa uma estimativa para o intervalo de
confiança de 95% para a média aritmética da população correspondente ao
comprimento do papel.
19
Estimativa do intervalo de confiança
da média aritmética
0,02
10,998  (1,96)
 10,998  0,00392
100
10,99408    11,00192
20
Estimativa do intervalo de confiança da
média aritmética
Construa uma estimativa para o intervalo de confiança de 99% para a média
aritmética do comprimento do papel.
0,02
10,998  (2,58)
 10,998  0,00516
100
10,99284    11,00316
21