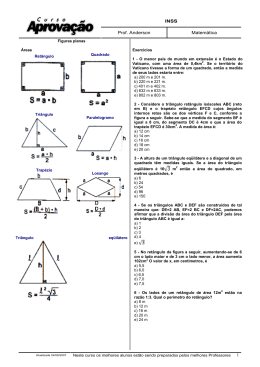
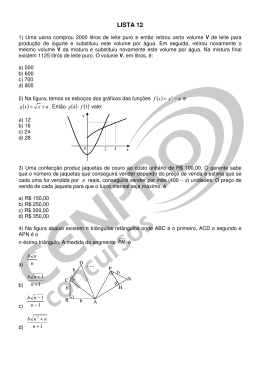
Geometria Plana – Recordando Pág. 39
Prof. Jefferson Ricart Pezeta
Vamos começar usando uma propriedade
aprendida no 9º ano, 8ª série, a qual dizia que a
altura relativa à hipotenusa de um triângulo ao
quadrado é igual ao produto das projeções dos
catetos. A partir desta propriedade, temos:
Alternativa d.
Primeiramente, vamos imaginar a figura
para que o exercício possa ficar mais
claro.
Muikto bem. Observe que, agora que sabemos o
valor de y, temos um triângulo retângulo ACD,
dos quais sabemos os valores dos dois catetos.
Desta forma, aplicando Pitágoras, podemos
calcular o valor de z.
Pronto. Agora nos resta apenas calcular o valor
de x. Observe que o enunciado diz tratar-se de
um triângulo retângulo. Analisando o desenho,
podemos perceber que ele é retângulo em A.
Desta forma, podemos aplicar o nosso velho
amigo Pitágoras novamente.
O comprimento total da correia é igual a 44cm.
Sabendo o valor do raio podemos calcular o
comprimento de cada circunferência. Observe
que a correia passa pela metade de cada polia,
ou seja, essas duas metades juntas representam
o comprimento de uma. Desta forma, temos:
A razão entre os perímetros é
determinada pelos lados. Logo, podemos
determinar os lados dos quadrados a
partir dos raios:
Agora, podemos estabelecer a relação
entre os lados:
Antes de começar, vamos desenhar a
figura conforme proposto pelo enunciado.
Calculamos acima então a parte da correia que
ocupa duas metades da polia. Sobra então a
parte que não toca na polia. Ambas as partes são
paralelas e de mesma medida.
Se chamarmos cada uma destas partes de d,
temos que as duas distâncias mais o
comprimento da circunferência é igual ao
cumprimento da correia, ou seja:
Agora que já temos a visão da figura,
vamos começar os cálculos.
a) Temos duas paredes medindo 3m x
5m, duas paredes medindo 3m x 7m e o
chão medindo 7m x 5m. Mas não
podemos deixar de observar que há uma
janela medindo 1m x 1m e uma porta
medindo 1m x 2m as quais não serão
pintadas. Desta forma, podemos calcular
a área total a ser pintada da seguinte
maneira.
b) Para o cálculo deste item podemos
estabelecer uma regra de três, ou seja,
se para cada 1 litro de tinta pinta-se 3
m2, 104m2 usarão x litros de tinta. Se
assim fizermos, obteremos:
Este exercício possui várias passagens. Primeiro
de tudo, vamos desenhar a bandeira.
a) Para calcularmos o valor total do
terreno, devemos primeiro calcular sua
área, lembrando que a área de um
trapézio equivale a área maior mais a
área menor vezes a altura, dividindo-se o
resultado por dois.
Agora que temos a metragem podemos
calcular o valor do terreno multiplicando a
área total pelo valor de cada metro
quadrado.
a) Perceba que a área verde é igual a área do
retângulo menos a área do losango. Desta forma,
temos:
b) Vamos então desenhar a figura
conforme proposto no enunciado.
Observe que os retângulos têm área
5*25= 125m2, enquanto a área do
retângulo vale (10*25)/2=125m2, ou
seja, as quatro área obtidas possuem a
mesma área.
b) Para responder a pergunta deste item
precisamos primeiro calcular a área da região
amarela. Observe que esta região equivale a área
do losango menos a área do círculo, ou seja:
A área total da bandeira pode ser calculada
somando-se a área da região amarela com a
região verde e o círculo, ou seja:
1,9209+0,4948+0,3850=2,8007
Para calcularmos a relação percentual entre a
área amarela e a área total da bandeira, basta
calcular o quociente entre elas.
Sabemos que a área de um quadrado é calculada
pelo produto lado x lado, ou pelo quadrado do
lado. Temos então:
Vamos nomear alguns pontos existentes
na figura. Você perceberá o quanto essa
ação irá nos ajudar.
Para calcularmos o valor de L, ou seja, o lado do
quadrado, basta colocarmos os dois lados da
igualdade em uma raiz quadrada.
A área da figura colorida representa a
área do quadrado menos a área de cada
parte não selecionada. Você pode estar
perguntado: “sim, e daí?”
Começaremos pela parte mais fácil. A
área do quadrado.
Ótimo. Vamos agora analisar cada parte
da figura não selecionada. Observe que
os pontos AEF formam um triângulo, no
qual a base AF equivale a 3 segmentos do
desenho e a altura AE a 2.
Vamos agora observar a área ocupada
pelos vértices FBHG. Observe que FNG
forma um triângulo de base FN
equivalente a 1 segmento e altura NG a 2
segmentos. A figura BHNG equivale a um
trapézio de base maior NG igual a 2
segmentos, base menor BH igual a 1 e
altura NB igual a 1. A área de FBHG é a
soma do triângulo FNG e do trapézio
FBHG.
Dando seqüência, vamos analisar quais
polígonos a área HIJC forma.
Primeiramente temos os pontos HCIO
formando um trapézio. A base maior HC é
igual a 3, a base menor IO é igual a 1, a
altura CO é igual a 1. Temos também a
formação do triângulo IOJ, o qual tem a
base JO valendo 2 e a altura IO valendo
1. Desta forma, temos:
Estamos quase finalizando. Agora vamos
analisar a área formada pelos pontos
JLMED. Vamos começar pelo mais fácil.
Observe que EDJ forma um triângulo de
base DJ igual a 2 e altura ED também
igual a 2. Já LMJ também forma um
triângulo. Se você observar bem, a base
MJ forma a diagonal de um quadrado
Como a diagonal é calculada pelo produto
do lado pela raíz de 2 e, sendo o lado
desses quadrado valendo 1 segmento,
temos que a diagonal vale raíz de 2.
Analisando a altura vemos que temos a
soma da metade da diagonal com mais
uma diagonal. Assim sendo, temos o
cálculo de JLMED formado da seguinte
maneira:
Agora falta pouco. Para finalizar, temos
que a área selecionada equivale à
diferença da área do quadrado com a
soma de todas as áreas calculadas até
aqui.
Alternativa d.
Observe que temos aqui um caso de
semelhança de triângulos. Dessa forma,
podemos, por definição, perceber que a á
área do triângulo ABC está para a área do
triângulo ADE, assim como o segmento
BC está para o segmento DE. Temos aqui
um caso de razão e proporção, aplicados
com Teorema de Tales. Como a razão da
esquerda trata-se de área, devemos
elevar a razão da direita ao quadrado.
Você estudou estas definições na 8ª série,
9º ano, quando estudou Tales. Mas temos
um detalhe extremamente importante n o
enunciado. Observe que torna-se claro
que as áreas das do triângulo ADE e do
trapézio CDEF são iguais. Esta afirmação
nos permite então dizer que a área do
triângulo ABC vale duas vezes o triângulo
ADE, ou seja, é o dobro. Desta forma,
podemos concluir que:
Ainda tem dúvidas sobre algum exercício esta página. Poste no blog ou me pergunte em sala
de aula.