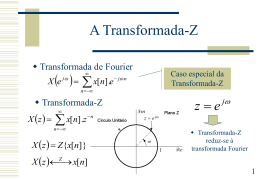
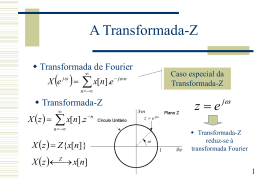
Transformada-Z
• Introdução
• Transformada Z
• Região de Convergência
• A Transformada Z inversa
• Propriedades da Transformada-Z
1
Transformada Z
• Função: É um operador linear útil para análise de sistemas
lineares e invariantes no tempo e para resolver equações
diferenças.
• Definição: A transformada Z de uma sequência discreta x(n) é
dado por

Z x( n )  X ( z )   x( n )z n
n  
– Notação:
x[ n ]  X ( z )
– A variável z é geralmente complexa e,
– A Transformada Z é uma série de potência, que pode ou não
convergir .
– O espaço do plano complexo para o qual ela converge define a
2
região de convergência.
Transformada Z
Z 2 x(n)  X ( z ) 

n
x
(
n
)
z

n  
Região de Convergência da Transformada Z (ROC)
• A região de convergência da transformada Z especifica onde X(z)
é definida. Geralmente, uma ROC é especificada como parte da
transformada Z.
• A ROC de X(z) é definida sobre uma região de um anel, centrado
na origem de um plano complexo: X(z) converge para
R  | z | R 
R   0 e/ou R   .
Im
A ROC é delimitada por pólos
Pólos: valores que anulam o
denominador de X(z).
Re
R-
R+
3
Transformada Z
Relação com a transformada de Fourier
X(e
j

)   x( n )e

 jn
X ( z )   x( n )z n
n  
n  
Expressando a variável z na forma polar, tem-se:
z  re j
X (re
j
)
r z
onde


 x[n] re
j

n
n  


 x[n]r
n  
Portanto, a transformada de Fourier
é um caso particular da transformada
Z, quando
r  z 1
n
e
 jn


n
 jn
(
x
[
n
]
r
)
e

n  
Im

1
Re
4
Seqüência Exponencial à Direita
• Uma ferramenta básica de análise usada na transformada Z
N1
N 2 1
N2
é a série geométrica.
r

r
n
S  r 
n N1
N
1

r
S   rn 
;
1 r
n 0
N 1

1 r
r 1
,
1
S  r 
, r 1
1 r
n 0
n
Exemplo: Determinar a transformada Z de x[n]=anu[n]

n n
Z ( a u [ n ])   a z
n
n 0
a nu( n ) 
1
,
1
1  az
Pólos: valores que
anulam o denominador
de X(z)

  ( az1 )n 
n0
1
, onde
1
1  az
z a
a
 1)
z
Im
a nu [ n ]
a
1
Re
....
0 1 2 3 4 5 6
n
5
Seqüência Exponencial à Esquerda
x(n)  anu(n 1),

X ( z )    a u( n  1) z
n
n  
( a  1)
n
1

a z
n n
n  
Se a 1 z  1 ou, equivalente, z  a
1
 a u( n  1 ) 
,
1
1  az
 a u[ n  1] ....
n

   a z 1   a n z n
n n
n 1
n 0
o somatório acima converge, e
1
 a 1 z
1
z
X ( z)  1 



1  a 1 z 1  a 1 z 1  az 1 z  a
n

Zeros: valores que
anulam o denominador
za
Im
-7 -6 -5 -4 -3 -2 -1 0
o
n
ax
1
6
Re
Propriedades da Transformada Z
• Pólos: valores que anulam o denominador de X(z) (raízes)
• Zeros: valores que anulam o numerador de X(z) (raízes)
• Supondo
Zx(n)  X ( z),
Zy(n)  Y ( z),
e seja
Rx | z | Rx
Ry | z | Ry
I xy  z : Rx | z | Rx  z : Ry | z | Ry 
• Propriedades:
Linearidade: Z ax( n )  by( n )  aX( z )  bY( z ), para z  I .
1
xy
A ROC pode ser expandida devido ao cancelamento de pólos e zeros.
7
Propriedades da Transformada Z
Zx(n)  X ( z),
Zy(n)  Y ( z),
• Supondo
Deslocamento:

Z x( n  n0 )   x( n  n0 )z
n  
Convolução: Se
n
Rx | z | Rx
Ry | z | Ry

  x( k )z k  no  z n0 X ( z )
k  

v[ n ]  x[ n ] * y [ n ]   x[ k ] y [ n  k ]
k  
Então
V ( z )  X ( z )Y ( z ) com z  I xy .
A ROC contém a interseção de Rx com Ry.
8
Sequência exponencial bi-lateral
n
n
 1
1
x [ n ]     u [ n ]    u [ n  1 ]
 3
2
n
 1
   u ( n) 
 3
1
1
, z 
1 1
3
1 z
3
n
1
1
1
   u( n  1 ) 
,z 
1
2
2
1  z 1
2
Assim pela propriedade da linearidade da transformada Z, tem-se
1
1
X( z ) 

,
1 1
1 1
1 z
1 z
3
2
1
1
 z 
3
2
1 1
Polos:  ;
3 2
1
Zeros : 0 ;
12
Im
1 1
1
z )
2 z( z  )
12
12
X( z ) 

1
1
1
1
( 1  z 1 )( 1  z 1 ) ( z  )( z  )
3
2
3
2
2( 1 
-1/3
Obs. Nenhum pólo pode estar dentro da ROC.
1/2 Re
9
Região de Convergência
A série de potência da transformada Z, X(z) não converge para todas
as seqüências ou valores de z. Para determinada sequência os
valores de z da transformada convergem para uma região chamada
de Região de Convergência (ROC).
Regiões de Convergência
Im
a
Im
1
Sequência à direita
(causal)
Re
a
Im
1 Re
Sequência à esquerda
(não-causal)
a
b
Re
Sequência Bilateral
10
Exemplo
n
 1
x[ n ]    u [ n ] 
2
1
n
a u( n ) 
,
1
1  az
 a nu( n  1 ) 
2n u[ n  1]
n
1
1
u
(
n
)

,
 
1 1
2
1 z
2
z a
1
, za
1
1  az
1
1

,

1
1 1 1  2 z
1 z
2
3 z 1

2
X( z ) 
,
1 1 

1

z  1  2 z 1

2


X( z ) 


2 n u( n  1 )  
z 
1
2
1
, z 2
1
1  2z
Im
1
 z 2
2
O
1/2 1 2
x
x
1
 z 2
2
11
Re
Importância da Especificação do ROC
• É importância especificar a ROC, pois ela é parte da transformada-Z.
• Na especificação da transformada Z, X(z), de uma sequência discreta
x(n), a ROC deve ser dada, uma vez que x(n) não poderá ser
encontrada se X(z) não tem a sua ROC especificada.
• Exemplo - Considere duas sequências
x[ n ]  anu( n )
y[ n ]  anu( n  1 )
então
1
X ( z) 
com | z || a |
1
1  az
Y ( z) 
1
com | z || a |
1
1  az
É importante entender que X(z)  Y(z).
• X(z) + ROC  x(n) única.
12
Diferentes tipos de sequência - ROC
• Duração Finita:
x(n)  0 para n  n0 e n  n1
ROC  {z : 0 | z | } , para
• À direita:
z  0 e/ou z  .
x( n )  0 para n  0
ROC  {z : R | z | }.
• À esquerda:
x( n )  0 para n  0
ROC  {z : 0 | z | R }.
• Bilateral:
ROC  {z : R | z | R }.
13
Outras Propriedades da ROC
• ROC é um anel ou um disco centrado na origem do plano z
complexo.
• Uma seqüência discreta x[n] tem transformada de Fourier se
somente se a ROC da transformada-Z de x(n) inclui o círculo
unitário.
• ROC não pode conter pólos.
• ROC deve ser uma região conectada, isto é, não pode ter
espaço vazios.
14
Estabilidade e Causalidade
• Função de Transferência : Se H(z) é a transforma Z de um
sistema linear com resposta ao impulso unitário h(n), i.e.,
• Teorema: Um sistema linear com função de transferência
racional Z h( n )  H ( z ) é causal e estável se e somente
se todos os pólos de H(z) estão localizados dentro do
círculo unitário.
Im


ROC


pmax

1
Re
Círculo unitário
15
Observação
• Supondo que
K
Ak
H( z )  
1
k 1 1  pk z
então h[n] pode ser escrito como
K
K
h( n )   Ak ( pk ) u( n )   hk ( n )
n
k 1
k 1
• Claramente, a transformada-Z de hk (n ) converge se
pk
1
z
• então, H(z) converge para todo z tal que
z  pmax  max pk .
1 k  K
• Obs. A ROC de um sistema H(z ) causal inclui o círculo
unitário.
16
Prova : Suficiência
• Suficiência: supondo que pk  1 para k  1,...,K. Então
K
h(n)   Ak ( pk )n u(n)
k 1
então
K
h(n)   Ak pk
e também
n
k 1


K
 h(n)  Ak pk
n 0
n 0 k 1
K

n
  Ak  pk  
k 1
n
n 0
então pk  1. Consequentemente H(z) é a função de
transferência do sistema estável.
17
Prova : Necessidade
• Necessidade: (pela contradição) Supondo que existe um polo
pi tal que | pi |>1. Claramente, o círculo unitário não está
incluído na ROC de H(z).
– Então, existe z0 com |z0|=1 tal que H(z0) não converge absolutamente.

H ( z0 )   h(n)( z0 ) n  
n 0
Uma vez que não existe tal z0 então a ROC não inclui o círculo unitário.
– Então

 h(n)(z )
n 0
0
H(z) não é estável.
n


  | h(n) || z0 |   h(n)  
n 0
n
n 0

H ( z0 ) ||z0 |1   h(n)
n 0
18
Properties of Z-Transform
Propriedades
1. Linearidade:
Sequência
Transformada Z
x[n], x1[n], x2 [n]
X ( z ), X1 ( z ), X 2 ( z )
ROC
Rx , Rx1 , Rx2
ax1[n]  bx2 [n]
aX1 ( z)  bX2 ( z)
containsRx1  Rx2
z  n0 X ( z )
Rx (*)
z0n x[n]
X ( z / z0 )
z0 Rx
4. Diferenciação:
nx[n ]
z
dX ( z )
dz
Rx (*)
5. Conjugado:
x * [n ]
X * ( z*)
Re{x[n]}
[ X ( z )  X * ( z*)]/ 2
containsRx
Im{x[n]}
[ X ( z )  X * ( z*)]/ 2 j
containsRx
6. Tempo Reverso:
x * [ n ]
X * (1 / z*)
1 / Rx
7. Convolução:
x1[n] * x2 [n]
X1 ( z) X 2 ( z)
containsRx1  Rx2
2. Deslocamento no Tempo: x[n  n0 ]
3. Multiplicação:
8. Teorema do Valor Inicial: x[n ]  0, n  0
lim X ( z )  x[0]
z 
Rx
19
Transformada Z Inversa
• Transformada-Z Inversa
X(z) + ROC  x(n) única.
• Métodos
– Usando o Teorema do resíduo
– Inspeção
– Expansões por frações parciais
• Pólos de primeira ordem
• Pólos de m-ésima ordem
20
Transformada Z inversa
1- Método de Inspeção: consiste simplesmente em reconhecer certos
pares de transformadas, por exemplo: Dado que
1
a u[n] 
,
1
1  az
Z
n
Se a ROC
| z || a |
a transformada inversa de
n
1
1
1
X ( z) 
, | z || | é x[n]    u[n]
1
2
 2
1  z 1
2
associada | z | 1 , então a transformada inversa
2
1
X ( z) 
,
1 1
1 z
2
1
| z || |
2
é de
n
é
1
x[n]    u[n  1]
 2
2- Método da expansão em frações parciais
Consiste em escrever qualquer função racional como uma soma de
frações parciais, de modo que para cada fração, a transformada Z
21
inversa seja facilmente reconhecida.
Suponha que X(z) é expressa como uma relação polinomial de z-1.
M
X ( z) 
 bk z
k
k 0
N
k
a
z
 k
ou equivalentemente
k 0
X ( z) 
M
z  bk z M k
N
k 0
N
z M  ak z N k
k 0
o que indica que tais funções têm M zeros e N pólos. Além disso
tem-se M - N pólos para z=0, se M >N e N - M zeros para z=0,
se N > M. Isso significa que o número de pólos e zeros são sempre
iguais, e não há pólos para z  . X(z) pode ser escrito na forma.
M
(1  ck z 1 )

b0 k 1
X ( z) 
N
a0 
(1  d z 1 )
k 1
onde ck são zeros e dk pólos (não nulos)
k
Se todos os M <N pólos são de primeira ordem, então:
N
Ak
X ( z)  
1
k 1 1  d k z
22
Multiplicando ambos os lados por (1 - dk z -1) e avaliando em z = dk
Ak  (1  dk z 1 ) X ( z )
z d k
Se M  N então deve-se escrever:
M N
X ( z )   Br z
r 0
r
N

k 1
Ak
1  d k z 1
Se X(z) tem pólos de ordem múltiplos, e M  N então a equação
deve ser modificada. Em particular, se X(z) tem um pólo de ordem s
em z=di. :
M N
N
s
Ak
Cm
r
X ( z )   Br z  

1
1
r 0
k 1,k i 1  d k z
m 1 1  d i z
Os coeficientes Cm podem ser obtidos da equação
 d s m

1
s
Cm 
(1  di w) X ( w) 
s m 
s m
( s  m)!(di )  di w
wd 1


i 23
Exemplo: Suponha que x[n] tem transformada Z dada por:
1  2 z 1  z 2
1  2 z 1  z 2
X ( z) 

3
1
1
1  z 1  z 2 (1  z 1 )(1  z 1 )
2
2
2
A ROC de X(z) é mostrado na figura
Como M = N =2, então X(z) pode ser escrito:
| z | 1
A1
A2

1 1 1  z 1
1 z
2
A constante B0 pode ser encontrada dividindo-se o numerador de X(z)
pelo denominador
3 1 1 2
1
2
1  2z  z 1  z  z
2
2
2  3z 1  z 2
2
X ( z )  B0 
 1  5 z 1
24
Dessa forma X(z) é escrito como:
 1  5 z 1
X ( z)  2 
1 1
(1  z )(1  z 1 )
2
 1  5 z 1
A1 
1  z 1
 1  5 z 1
A2 
1 1
1 z
2
X ( z)  2 
z
1
2
 1  10

 9
1 2
1 5

8
z 1
1
2
9
8

1 1 1  z 1
1 z
2
Usando a tabela de transformada Z
n
1

x[n]  2 [n]  9  u[n]  8u[n]
 2
25
Soluções possíveis para X(z)
1  2 z 1  z 2
9
8
X ( z) 
 2

3 1 1 2
1 1 (1  z 1 )
1 z  z
(1  z )
2
2
2
n
1

1. x[n]  2 [n]  9  u[n]  8u[n]
 2
| x | 1
Seqüência à direita
n
1

2. x[n]  2 [n]  9  u[n  1]  8u[n  1]
 2
| x | 1
Seqüência à esquerda
n
1

3. x[n]  2 [n]  9  u[n]  8u[n  1]
 2
Seqüência bilateral
1
| x | 1
2
26
Aplicação das propriedades da transformada Z
1
1
1.Determine a transformada inversa de X ( z ) 
, | z |
1
4
(z  )
Rescrevendo X(z), tem-se
4
4
1
z 1
1
X ( z )  4 
, | z |
X ( z) 
, | z |
1 1
4
1 1
4
(
1

z
)
(1  z )
4
4
Calculando a transformada inversa:

n
1

x[n]  4  4  u[n]
 4
Z
no
x
[
n

n
]


z
X ( z)
Usando a propriedade:
o


 1 
1
1
X ( z)  z 
 , | z |
4
 1  1 z 1 
 4 

1

x[n]   
 4
n 1
u[n  1]
27
2. Multiplicação por uma seqüência exponencial
1
Z
Dado que u[n] 
determinar a transformada Z de
1
1 z
1 j n
1  j n
x[n]  r cos( o n)u[n] x[n]  (re ) u[n]  (re ) u[n]
2
2
1 j o n
1/ 2
Z
(re ) u[n] 
,
| z | r
j o 1
2
1  re z
1  j o n
1/ 2
Z
(re
) u[n] 
,
| z | r
 j o 1
2
1  re
z
n
1/ 2
1/ 2
X ( z) 

,
jo 1
 jo 1
1  re z
1  re
z
(1  r coso z 1 )
X ( z) 
,
1
2 2
1  2r coso z  r z
| z | r
| z | r
28
dX ( z )
Z
z
3. Diferenciação de X(z) nz[n] 
dz
Exemplo:
X ( z)  log(1  az1 ) ,
dX ( z )  az2

dz
1  az1
| z || a |
dX ( z )
az1
nx[n]   z

dz
1  az1

Z
Consultando a tabela de transformada Z e usando a propriedade do
deslocamento no tempo,tem-se
nx[n]  a(a)n1u[n 1]
Portanto,
x[n]  (1)
n 1
an
Z
u[n  1] 
log(1  az1 )
n
exemplo:
x[n]  nanu[n]  n(a nu[n])
az1
X ( z) 
(1  az1 ) 2

| z || a |
X ( z)   z
d  1 
| z | a

1 
dz  1  az 
29
4. Tempo reverso
Z
x[n] 

X (1/ z) ,
ROC  1/ RX
Exemplo: determinar a transformada Z de
1
Z
Dado que: a nu[n] 
, | z || a |
1
x[n]  a  nu[n]
1  az
1 1
1

a
z
Z
1
x[n]  a nu[n] 

,
|
z
|

|
a
|
1 1
1  az 1  a z
5. Convolução de sequências - Exemplo
Sejam x1[n]  a nu[n] e x2[n]  u[n]. Determine a transformada Z
de x1[n]  x2 [n].
Z
X1 ( z) X 2 ( z )
Pela propriedade da convolução no tempo: x1[n]  x2[n] 
1
, | z || 1 | ,
| a | 1
| z || a |
1
1 z
1

Y ( z )  X ( z1 ) X ( z2 ) 
1 
1
1
1

 , | z | 1
Y
(
z
)

(1  az )(1  z )
1
1 

1  a  (1  az )(1  z ) 
1
30
y
[
n
]

(u[n]  a n1u[n]
Portanto:
1 a
1
a u[n] 
,
1
1  az
n
Z
Z
u[n] 
6. Teorema do valor inicial
Se x[n] é uma sequência à direita, isto é x[n]=0, para n < 0, então

X ( z )   x[n]z  n  x[0]z 0 x[1]z 1  x[2]z  2  2  x[3]z 3  .....
n 0
lim X ( z )  x[0]
z 
Exemplo: Quais das transformadas Z poderiam ser a transformada
de uma sequência causal (sem resolver)
(1  z 1 ) 2
a) X ( z ) 
(1  0,5z 1 )
( z  1) 2
b) X ( z ) 
( z  0,5)
( z  0,25)5
c) X ( z ) 
( z  0,5)6
( z  0,25)6
d ) X ( z) 
( z  0,5)5


lim X ( z )  1
z 
lim X ( z )  
z 


lim X ( z )  0
z 
lim X ( z )  
z 
31
Exemplo de Solução via Transformada Z
• Problema: Dado que y(0)=1. Considere a equação diferença
y(n  1)  2 y(n)  u(n).
• Solução: Aplicando a transformada Z dos dois lados:
zY ( z )  2Y ( z )  U ( z )
– Direito =
– Esquerdo =

U ( z )   1z
n 0
n
1
z


1
z 1
1 z
zY ( z )  2Y ( z )  Y ( z )( z  2 )
z
z 1
– Resolvendo:
Y( z ) 

( z  1 )( z  2 ) ( 1  z 1 )( 1  2 z 1 )
(pela expansão em frações parciais)
1 1
1
1
Y( z ) 

1
3 1 z
3 1  2 z 1
– Transformada Z inversa
1
1
y( n )  u( n )  ( 2 )n u( n )
3
3
32
Exemplo
Considere um sistema LTI com entrada x[n] e saída y[n] que satisfaz a equação
diferença:
5
y[n ]  y[n  1]  y[n ]  x[n ]  x[n  1]
2
Determine todas as possíveis respostas do sistema ao impulso unitário h[n] .
Y ( z )(1 
5 1 2
z  z )  X ( z )(1  z 1 )
2
Y ( z)
(1  z 1 )
(1  z 1 )
2/3
1/ 3
H ( z) 




X ( z ) (1  5 z 1  z 2 ) (1  2 z 1 )(1  1 z 1 ) (1  2 z 1 ) (1  1 z 1 )
2
2
2
2 n
1 1 n

z

1
/
2
h
(
n
)


2
u
[

n

1
]

( ) u[ n  1]  h[0]  0

3
3 2

2
1 1
1
1/ 2  z  2
h( n )   2n u[ n  1]  ( ) n u[n ]
 h[0] 


3
3 2
3
ROC  
2
1 1
 z 2
h( n )  2n u[n ]  ( ) n u[n ]
 h[0]  1
3
3 2

2
1 1
2

No
h( n )  2n u[n ]  ( ) n u[ n  1]
 h[0] 

3
3 2
3

33