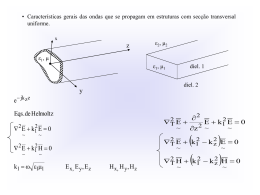
MOVIMENTO OSCILATÓRIO











Movimentos oscilatórios periódicos
Movimento harmónico simples (MHS)
Sistema massa-mola
Representação matemática do MHS
Representação gráfica do MHS
Definição de frequência e período
Equações de movimento do MHS
Energia no MHS
Pendulo simples
Oscilações amortecidas
Oscilações forçadas
1
MOVIMENTO OSCILATÓRIO
Estamos familiarizados com diversos tipos de movimentos oscilatórios periódicos
2
mais exemplos de movimento oscilatório
3
outros exemplos de movimento oscilatório
Vibrações atómicas e moleculares para estados excitados
Eletrões vibram em torno do núcleo
frequência alta: ~1014 - 1017 Hz
Os núcleos das moléculas vibram
frequência intermediária: ~1011 - 1013 Hz
4
Vibrações das moléculas de água
5
Ligações de átomos de carbono com hidrogénio são importantes na
química da vida
Vibrações CH2
Symmetrical
stretching
Antisymmetrical
stretching
Scissoring
Rocking
Wagging
Twisting
6
mais exemplos de movimento oscilatório
Os átomos num sólido não estão completamente imóveis.
Eles vibram com uma amplitude pequena em torno da sua posição de equilíbrio
7
MOVIMENTO PERIÓDICO
O movimento periódico é o movimento dum corpo que se repete regularmente
O corpo volta a uma dada posição depois dum certo intervalo de tempo fixo
O MOVIMENTO HARMÓNICO SIMPLES (MHS)
É um tipo especial de movimento periódico e acontece quando a força que age sobre
a partícula
• é proporcional ao deslocamento da partícula em relação a posição de equilíbrio
• e é dirigida sempre para a posição de equilíbrio
Fs  kx
 Lei de Hooke
8
MOVIMENTO DO SISTEMA MASSA-MOLA
Um bloco de massa m é ligado a uma mola
O bloco se desloca numa superfície horizontal
sem atrito
Quando a mola não está esticada nem
comprimida, o bloco está na posição de
equilíbrio x = 0
Vimos anteriormente que pela Lei de Hooke que
Fs  kx
k é a constante elástica
Fs
 força restauradora
x 
deslocamento
A força restauradora está sempre dirigida
para o ponto de equilíbrio  é sempre oposta
ao deslocamento
O movimento do sistema massa-mola é um movimento harmónico simples
9
•
O bloco é deslocado para a direita de
x=0
– A posição é positiva
A força restauradora é dirigida para a
esquerda
•
•
•
•
•
•
O bloco está na posição de equilíbrio
x=0
A mola não está nem esticada nem
comprimida
A força é 0
O bloco é deslocado para a esquerda
de x = 0
– A posição é negativa
A força restauradora é dirigida para a
direita
10
ACELERAÇÃO
De acordo com a segunda lei de Newton
k
Fs  ma  -kx  ma  a   x
m
A aceleração é proporcional ao deslocamento do bloco
O sentido da aceleração é oposto ao sentido do deslocamento (sinal menos)
Num corpo que se mova com um movimento harmónico simples (MHS), a aceleração é
proporcional ao seu deslocamento mas tem um sentido oposto ao deslocamento
A aceleração não é constante  as equações cinemáticas não podem ser aplicadas
Se o bloco é largado de uma posição x = A, então a aceleração inicial é
O bloco continua até x = - A onde a sua aceleração é
Quando o bloco passa pelo ponto de equilíbrio,
a
a
k
A
m
k
A
m
a0
11
MOVIMENTO DO BLOCO
O bloco continua a oscilar entre –A e +A
A força é conservativa
Na ausência de atrito, o movimento continua para sempre
Sistemas reais estão sujeitos a atrito, portanto não oscilam indefinidamente !
12
REPRESENTAÇÃO MATEMÁTICA DO MOVIMENTO HARMÓNICO SIMPLES
Tratamos o bloco como sendo uma partícula
Escolhemos que a oscilação ocorre ao longo do eixo
Aceleração 
 a   x
2
d 2x
k
a 2  x
dt
m
ou
x

Definimos
2 
k
m
d 2x
2



x
2
dt
Precisamos de uma função que satisfaça a equação diferencial de segunda ordem
Procuramos uma função x(t) cuja segunda derivada é a mesma que a função original
2
com um sinal negativo e multiplicada por 
AS FUNÇÕES TRIGONOMÉTRICAS SIN E COS RESPEITAM ESTES REQUISITOS !
Podemos construir uma solução com uma ou ambas as funções
13
Funções seno e cosseno
14
REPRESENTAÇÃO GRÁFICA
A seguinte função cos é uma solução da equação
xt   A cost   
onde
A,  e 
são constantes
A é a amplitude do movimento esta é
a posição máxima da partícula quer na
direção positiva quer na negativa
 é a frequência angular
Unidade: rad/s

é a fase (constante) ou o
ângulo de fase inicial
 0
•
Se a partícula está em x = A para t = 0, então
•
A fase do movimento é a quantidade
•
x(t) é períodica e o seu valor é o mesmo cada vez
que t aumenta de 2 radianos
t   
15
EXPERIÊNCIA
A caneta ligada ao corpo oscilante desenha
uma curva sinusoidal no papel que está em
movimento
Verifica-se assim a curva cosseno, considerada anteriormente
16
DEFINIÇÕES
•
O período, T, é o intervalo de tempo
necessário para que a partícula faça um ciclo
completo do seu movimento
Os valores de x e v da partícula no instante t
são iguais aos valores de x e v em t + T
T
•
2

O inverso do período chama-se frequência
A frequência representa o nº de oscilações executadas pela partícula por unidade
de tempo
1 
ƒ 
T 2
•
A unidade é o ciclo por segundo = hertz (Hz)
17
EQUAÇÕES DO MOVIMENTO NO MHS
xt   A cost   
dx
v
 A sin t   
dt
d 2x
a  2   2 A cost   
dt
vmax
k
 A 
A
m
amax
k
 A A
m
2
18
ENERGIA NO MHS
Energia do sistema massa-mola
• Energia cinética
K  12 mv2  12 m A sin t    
2
1
2
2 2
2
t   

A
sin
2
k

onde  2 
k
k
 m 2
m

assim
K  12 kA2 sin 2 t   
• Energia Potencial
U  12 kx2  12 k  A cost    
2
U  12 kA2 cos 2 t   
19
• Energia Mecânica
EM  K  U 
1
2
1
2
mv  kx
2
1
2
2
kA2 sin 2 t     12 kA2 cos2 t   

EM  kA
1
2
2
20
Pêndulo simples
O pêndulo simples também
pode exibir um movimento
harmónico simples (MHS)
O MHS acontece quando o
fio faz um ângulo pequeno
com a vertical
 pequena oscilação
21
Pêndulo simples
O comprimento, L, do pêndulo é constante
Forças que atuam sobre a esfera:


Peso  P  mg

Tensão T
Força tangencial (força restauradora)
d 2s
Ft  mg sin   m 2
dt
d 2
g
(s  L )
  sin 
2
dt
L
Para ângulos pequenos,
d 2
g
 
sin    
2
dt
L
Este resultado confirma que o movimento é o MHS
 sistemamassa - mola


d 2x
k


 x
2
dt
m


22
A função  que satisfaz a equação diferencial:
d 2
g
 
2
dt
L
é
 sistema massa - mola


 x  A cos(t   ) 
  max cos(t   )
onde

2
g
L
L
T
 2

g

é a frequencia angular

o período
23
Exemplo 1: Considere um pêndulo de comprimento
bola está presa a uma mola de constante
simultaneamente em equilíbrio. Determine
k.
L
com uma bola de massa
M.
Admita que o pêndulo e a mola estão
 para pequenas oscilações.
Resolução
Fpendulo  Mg sin   Mg
Fmola  kx  kL sin   kL
x
Força resultante que atua sobre a bola:
Ma  Fpendulo  Fmola  Mg  kL 

L
M
k
g
Mg 
kL   ML 
L
M
L M
 ML 2
onde
A

 

g k 
g k 


  
   
L M 
L M 
2
24
OSCILAÇÕES AMORTECIDAS
Nos sistemas realistas, estão presentes o ATRITO
indefinidamente
 o movimento não oscila
Neste caso, a energia mecânica do sistema diminui no tempo e o movimento é
conhecido como movimento amortecido
Um exemplo de movimento amortecido

um corpo está ligado a uma mola e
submerso num líquido viscoso
A força de atrito pode ser expressa como
Fatrito  bv
b  é o coeficiente de amortecimento
v  a velocidade do corpo de massa m
(no fluido o atrito é proporcional à v )
A equação do movimento amortecido é
F  ma  kx  bv
d 2x
dx
m 2  kx  b
dt
dt
25
OSCILAÇÕES AMORTECIDAS
A função x que satisfaz a equação diferencial:
x  Ae

b
t
2m
cos(t   )
onde
d 2x
dx
m 2  kx  b
dt
dt

k  b 


m  2m 
é
2
Exemplo
Animations courtesy of Dr. Dan Russell, Kettering University
26
OSCILAÇÕES FORÇADAS
É possível compensar a perda de energia de um sistema amortecido aplicando uma
força externa
A amplitude do movimento permanecerá constante se o
aumento de energia for igual à diminuição da energia
por cada ciclo.
Exemplo
F
F  F0 cos  f t
A equação do movimento
oscilações forçadas é
amortecido
para
d 2x
dx
m 2  kx  b  F0 cos  f t
dt
dt
Animations courtesy of Dr. Dan Russell, Kettering University
27
A amplitude de uma oscilação forçada é
A

 onde  0 é a frequência angular
natural do oscilador
F0 m
2
f

 02  4 2 2f
2
 onde  f é a frequência angular da
força aplicada no oscilador
RESSONÂNCIA
Quando a frequência angular da força aplicada (frequência forçada)é igual à
frequência angular natural ( f  0 ) ocorre um aumento na amplitude

A


A
F0 m
2
f


2 2
0
 4 
2
2
f

Amáximo
Chama-se RESSONÂNCIA a esse
aumento espectacular na amplitude

(0  0  0)
28
Exemplo 2:Tacoma bridge
Em 1940 ventos constantes causaram vibrações na ponte de Tacoma desencadeando
sua oscilação numa frequência próxima de uma das frequências naturais da estrutura
da ponte.

Foi estabelecida a condição
de ressonância (
f  0 )
a ponte caiu



29