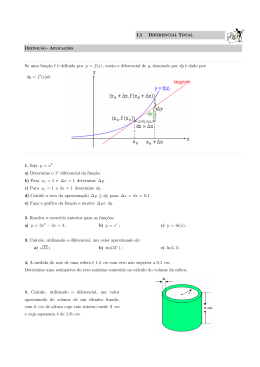
18
3 - Diferencial
3.1 – Plano tangente
O plano tangente a uma superfície z = f(x,y) no ponto (x0, y0,f(x0,y0)) é dado por:
z − f ( x0 , y0 ) =
∂f
∂f
( x0 , y0 ).( x − x0 ) + ( x0 , y0 ).( y − y0 )
∂x
∂y
Exemplo 1: Determinar o plano tangente a superfície z = x2+y2 nos pontos P(0,0,0) e
Q(1,1,2).
• No ponto P(0,0,0) temos
f(x0,y0) = f(0,0) = 02 + 02 = 0
∂f
∂f
= 2x ⇒
(0,0 ) = 2.0 = 0
∂x
∂x
∂f
∂f
= 2y ⇒
(0,0) = 2.0 = 0
∂y
∂y
Então: z – 0 = 0.(x – 0) + 0.(y – 0 )
Plano tangente
•
No ponto Q(1,1,2) temos
z=0
f(x0,y0) = f(1,1) = 12 + 12 = 2
∂f
∂f
= 2x ⇒
(1,1) = 2.1 = 2
∂x
∂x
Então: z – 2 = 2.(x – 1) + 2.(y – 1 )
Plano tangente
∂f
∂f
= 2y ⇒
(1,1) = 2.1 = 2
∂y
∂y
z = 2x + 2y –2
Exemplo 2: Determine a equação do plano tangente a superfície y = 6 - x2- y2 no ponto
(0,1,5)
3.2 - Diferencial
A diferencial de uma função de uma variável, y = f(x), é aproximadamente igual ao
acréscimo ∆y da variável dependente y. De forma análoga a diferencial de uma função de
duas variáveis, z = f(x,y), é uma função ou transformação linear que melhor aproxima o
acréscimo ∆z da variável dependente z.
Geometricamente o plano tangente à superfície z = f(x,y), no ponto (x0,y0), quando
existe, é o plano que “melhor aproxima” a superfície perto do ponto (x0,y0).
Definição: Seja z = f(x,y) uma função diferenciável no ponto (x0,y0). A diferencial de f em
(x0,y0) é definida pela função ou transformação linear
T: R2 → R
∂f
∂f
( x0 , y0 ).( x − x0 ) + ( x0 , y0 ).( y − y0 )
∂x
∂y
∂f
∂f
ou T (h, k ) =
( x0 , y0 )h + ( x0 , y0 )k
∂x
∂y
onde h = x-x0 e
k = y - y0
T ( x − x0 , y − y0 ) =
19
∂f
∂f
( x0 , y0 ).( x − x0 ) + ( x0 , y0 ).( y − y0 ) é a diferencial de f em (x0,y0)
∂x
∂y
relativa aos acréscimos ∆x e ∆y , onde
É comum dizer que
∆x = x - x0 e
∆y = y - y0
Numa notação clássica, definimos a diferencial das variáveis independentes x e y como os
acréscimos ∆x e ∆y, respectivamente
dx = ∆x
dy = ∆y
Assim a diferencial de f em (x,y), relativa aos acréscimos ∆x e ∆y , é indicada por dz ou df,
onde
dz =
∂f
∂f
( x, y )dx + ( x, y )dy
∂x
∂y
É também chamada de diferencial total de f(x,y))
3.3 – Diferencial de uma função de três variáveis
dw =
∂f
∂f
∂f
( x, y, z )dx + ( x, y, z )dy + ( x, y, z )dz
∂x
∂y
∂z
Exemplos:
1) Variação da área do retângulo quando a base b varia de 4 cm para 4,01 cm e a altura h varia
de 2 cm para 2,1 cm.
2) O mesmo retângulo quando a base b varia de 4 cm para 4,01 cm e a altura h varia de 2 cm
para 1,8 cm.
3) Seja uma caixa cilíndrica com r = 2 cm e h = 5 cm. O custo do material usado em sua
confecção é de R$ 0,81 por cm2. Se as dimensões sofrerem um acréscimo de 10% no raio e
2% na altura, pergunta-se:
a) valor aproximado do acréscimo no custo da caixa.
b) Valor exato do acréscimo no custo da caixa.
3.4 – Exercícios
1) Calcular a diferencial de f ( x, y ) = x + xy no ponto (1,1).
2) Determinar uma boa aproximação para o acréscimo da variável dependente da função
z = x2 + y2 - xy quando (x,y) passa de (1,1) para (1,001; 1,02)
20
3) Calcular ∆z para a variação do exercício (2) e compare os valores.
4) Calcular a diferencial das funções nos pontos indicados:
a) f(x,y) = ex cos y; P(1,π/4)
b) z = ln(x2 + y2); P(1,1)
c) w = x.e2z + y;
P(1,2,0)
5) Calcular a diferencial total de:
a) z = sen2 xy
x
b) z = arctg
y
c) t = xy – yz + zw
x2 + y2
d) z =
x+ y
V2
watts. Se V = 120 volts
R
e R = 12 ohms, calcular um valor aproximado para a variação de energia quando V
decresce de 0,001 volts e R aumenta de 0,02 ohms.
6) A energia consumida num resistor elétrico é dada por P =
7) Um terreno tem a forma retangular. Estima-se que seus lados medem 1200 m e 1800
m, com erro máximo de 10 m e 15 m, respectivamente. Determinar o possível erro no
cálculo da área do terreno.
8) Uma lata cilíndrica de estanho deve ter raio interno de 2 dm e altura interna de 4 dm,
sendo de 5 mm a espessura das paredes. Encontrar o volume aproximado do estanho
necessário para fabricá-la usando diferenciais.
9) Usando diferencial, obter o aumento aproximado do volume de um cilindro circular
reto, quando o raio varia de 3 cm para 3,1 cm e a altura varia de 21 cm para 21,5 cm.
10) Um material está sendo escoado de um recipiente formando uma pilha cônica. Num
dado instante, o raio da base é de 12 cm e a altura 8 cm. Usando diferencial, obter uma
aproximação da variação do volume, se o raio da base varia para 12,5 cm e a altura
para 7,5 cm. Comparar o resultado obtido com a variação exata do volume.
11) Considerar um retângulo com lados a = 5 cm e b = 2 cm. Como vai variar,
aproximadamente, a diagonal desse retângulo se o lado a aumentar 0,001 cm e o lado
b diminuir 0,2 cm
Respostas: 1) dz = 3/2dx + 1/2dy
2) dz = 0,021 3) ∆z = 0,021381; Erro = 0,000381
2
2
4) a)
edx −
edy
b) dx + dy
c) dx + dy + 2dz
2
2
5) –2,002 wats
6) 36 000 m2
7) 17,1π cm3
8) 3,77 dm3
21
3.5 – Regra da Cadeia
Usamos a regra da cadeia para calcular a derivada de funções compostas.
Sejam A e B conjuntos abertos em R2 e R, respectivamente, e sejam z = f(x,y) uma
função que tem derivadas parciais de 1a. ordem contínuas em A, x = x(t) e y = y(t) funções
diferenciáveis em B tais que para todo t є B temos (x(t(, y(t)) є A.
Seja a função composta
h(t) = f (x(t), y(t)),
t є B.
Então, essa função composta é diferenciável para todo t є B e dh/dt é dada por:
dh ∂f dx ∂f dy
= . + .
dt ∂x dt ∂y dt
Exemplos: 1) Calcule a derivada parcial da função:
f(x,y) = xy + x2, sendo x = t + 1 e y = t + 4
3.6 – Exercícios
dh ∂f dx ∂f dy
= . + .
para as funções:
dt ∂x dt ∂y dt
a) f(x,y) = ln (x2 + y2), sendo x = 2t + 1 e y = 4t2 – 5
1) Verificar a regra da cadeia
b) f(x,y) = sen (2x + 5y), sendo x = cos t e y = sen t
c) f(x,y) = x.e2xy , sendo x = 2t e y = 3t – 1
2) Determinar dz/dt usando a regra da cadeia
a) z = tg (x2 + y), x = 2t, y = t2
b) z = x cosy, x = sen t, y = t
c) z = arc tg xy, x = 2t, y = 3t
d) z = ex (cos x + cos y), x = t3, y = t2
e) z =
x
, x = e-t, y = ln t
y
f) z = xy, x = 2t2 + 1, y = sen t
3) Se f(x,y) = x3y – y4, sendo x = 1/t e y = lnt, obtenha
df
dt
22
4) Sendo z = yex+ xey, e x = cosu e y = senu, calcule
Respostas: 1) a)
32t 3 − 36t + 2
8t 4 − 18t 2 + 2t + 13
2) a) 10t sec2(5t2)
b) cos2t – sen2t
3
d) tet [−3t sen t 3 + 3t cos t 3 + 3t cos t 2 − 2 sen t 2 ]
f) 4tsent + (2t2 + 1)cost
3)
− 3 ln t 1 4 ln 3 t
+ 4−
t4
t
t
4) ecosu(cosu – sen2u) + esenu(cos2u – senu)
dz
du
b) cos(2cost + 5sent)[-2sent + 5cost]
12t
1 + 36t 4
− e−t
e−t
e)
−
ln t t ln 2 t
c)