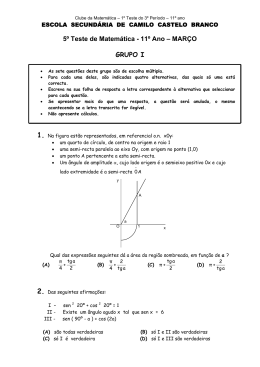
Um modelo de mínimos quadrados para a audição humana CIn - UFPE Lucas Vicente Tenório Rafael Farias Marinheiro Tomás Arruda de Almeida Método dos mínimos quadrados β’ O método tem como objetivo calcular a melhor função considerando que a média do quadrado das distancias entre os pontos e a função seja a menor possível. A função π π π, π = π¦π β π β ππ₯π 2 π=1 rege a curva que satisfaz os objetivos do método. Sendo: π₯π e π¦π coordenadas dos pontos iniciais. πeπ coeficientes. β’ π e π definidos por: π = π¦ β ππ₯ π= π π=1(π₯π β π₯)(π¦π β π π=1(π₯π β π₯)² π¦) Onde π¦ é a média amostral de π¦π e π₯ é a média amostral de π₯π . Séries de Fourier Combinações lineares β’ Seja g uma função real contínua em π, π . Suponha que exista um conjunto de funções reais contínuas em π, π , chamado de π½ π½ = π1, π2, π3, β¦ tal que π = π1 π1 + π2 π2 + π3 π3 + β¦ π½ existe? Como encontrar os coeficientes da combinação linear? Produto interno β’ Dadas duas funções π e π pertencentes ao espaços das funções reais contínuas em [π, π]. Podemos definir π π, π = π π‘ π π‘ ππ‘ π onde π, π é o produto interno de π e π. Essa expressão satisfaz todas as mesmas condições do produto interno com vetores em βπ . Projeções β’ Seja π½ = π£1 , π£2 , π£3 , β¦ uma base ortogonal de um espaço π munido de produto interno. Tome o vetor π’ π π. Podemos escrever π’ da seguinte forma: π’ = π1 π£1 + π2 π£2 + π3 π£3 + β¦ Fazendo o produto interno de π’ com π£π , obtemos: π’, π£π ππ = π£π , π£π Projeções β’ Considerando que exista uma base ortogonal π½ para o espaço das funções reais contínuas em π, π , então podemos aplicar o resultado que foi explicitado: π, ππ ππ = ππ , ππ ππ = π π π π π π π π π‘ π π‘ ππ‘ π‘ ππ π‘ ππ‘ Séries dos cossenos β’ O conjunto 1 ππ‘ 2ππ‘ πππ‘ 2 , cos πΏ , cos πΏ , β¦ , cos πΏ , β¦ é uma base ortogonal para o espaço das funções reais contínuas em 0, πΏ . β πππ‘ π π‘ : 0, πΏ β π π‘ = π0 + ππ cos πΏ π=1 πΏ πππ‘ π π‘ cos ππ‘ 0 πΏ ππ = πΏ πππ‘ cos² ππ‘ 0 πΏ Séries dos senos β’ O conjunto ππ‘ 2ππ‘ πππ‘ sen , sen , β¦ , sen ,β¦ πΏ πΏ πΏ é uma base ortogonal para o espaço das funções reais contínuas em 0, πΏ . β πππ‘ π π‘ : 0, πΏ β π π‘ = ππ sen πΏ π=1 πΏ πππ‘ π π‘ sen ππ‘ 0 πΏ ππ = πΏ πππ‘ sen² ππ‘ 0 πΏ Séries de Fourier β’ O conjunto 1 ππ‘ 2ππ‘ πππ‘ ππ‘ 2ππ‘ πππ‘ 2 , cos πΏ , cos πΏ , β¦ , cos πΏ , β¦ , sen πΏ , sen πΏ , β¦ , sen πΏ , β¦ é uma base ortogonal para o espaço das funções reais contínuas em βπΏ, πΏ . β β πππ‘ πππ‘ π π‘ : βπΏ, πΏ β π π‘ = π0 + ππ cos + ππ sen πΏ πΏ π=1 ππ = πΏ πππ‘ π π‘ cos ππ‘ βπΏ πΏ πΏ πππ‘ cos² ππ‘ βπΏ πΏ ππ = π=1 πΏ πππ‘ π π‘ sen ππ‘ βπΏ πΏ πΏ πππ‘ sen² ππ‘ βπΏ πΏ Exemplo
Download
