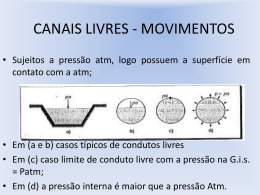
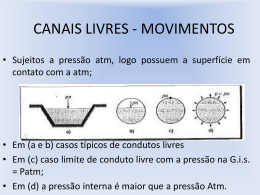
Aula Teórica 17
Turbulência. Equações do
escoamento turbulento.
Equação
ui
ui
ui
p


 u j



 g i
t
x j
xi x j x j
ui  ui  ui'
substituindo
ui'u 'j
ui
ui
ui
p


 u j




t
x j
xi x j x j
x j
 g i
Dedução da Equação
ui
ui
ui
p


 u j



 g i
t
x j
xi x j x j
ui  ui  ui'
substituindo


ui
 ui  ui'
ui
ui'
 ui 





t
t
t
t
t
'
'


u
u


u

u
u

u
u
j i
j
j
i
i
u j i 


x j
x j
x j

u j ui
x j

ui'u 'j
x j

u j ui'
x j


ui u 'j
x j


u j ui
x j

ui'u 'j
x j
Equação
u j ui
ui


t
x j
ui
p





xi x j x j
ui
ui
p


 u j


t
x j
xi x j
Tensões de
origem
viscosa

 ui' u 'j
x j
 g
i
 ui

'
'

 ui u j   g i
 x

j


Tensões de origem
Turbulenta ou de
Reynolds
Significado das Tensões de Reynolds
ui u j ui
u j


x j
x j
u j ui
x j

ui'u 'j
x j

u j ui'
x j

ui u 'j
x j

u j ui
x j

ui'u 'j
x j
• As tensões de Reynolds provêm do termo convectivo
(de inércia) e são proporcionais às forças de inércia: U 2
• Dão origem a mistura porque o termo convectivo
representa a divergência do fluxo advectivo: “o que sai
menos o que entra”. Sendo a entrada e saída
aleatórias, o resultados é a mistura.
Adimensionalização da tensão de corte
U

 U 2


1
*
te
D
 f 


C 
 C te
1
1
UD
Re
2
U
U 2
2
2
• Representando o coeficiente de atrito em função do
Reynolds, em coordenadas logarítmicas obtemos uma
recta decrescente enquanto o escoamento é laminar
e uma constante em turbulento.
• Porque é que o coeficiente de atrito tende para uma
constante?
• A constante depende da intensidade de turbulência
que é dependente da rugosidade do tubo.
• Quando o escoamento passa de laminar a turbulento,
o coeficiente de atrito aumenta.
Diagrama de Moody
Equação de Colebrook
Problema
• Considere o escoamento de água, num tubo cilíndrico de
aço galvanizado, completamente desenvolvido, de
diâmetro 5 cm, com velocidade média de 2 m/s.
• a) calcule o caudal.
• b) calcule o Nº de Reynolds e a rugosidade relativa.
• c) determine o coeficiente de atrito e a perda de pressão
num troço de 100 metros de comprimento.
• e) Qual a energia dissipada por unidade de volume?
• d) qual a potência que uma bomba deveria fornecer ao
fluido?
• e) qual a potência que o motor deve de fornecer à bomba?
Equação de Bernoulli Generalizada
1
1
1




2
2
2
 P  U  gz   w   P  U  gz    U ki
2
2

1

2 i 2
Tubo
4 fL
k
D
Equação de uma instalação
1
1




2
2
 P  U  gz 
 P  U  gz 
1
2
2

1 w 
2


  U 2 ki
g
g
g
i 2g
 P

 P

1 2
1 2
1


U  z   H  

U  z    U 2 ki
 g 2 g
1
 g 2 g
2 i 2 g


P P
1
U 2 2  U1 2  z2  z1    1 U 2 ki
H   2 1 
2g
i 2g
 g

U
Q
Q

A D 2
4
se :
k  C te
H  h  KQ 2
Ponto de funcionamento de uma
bomba
H
Q