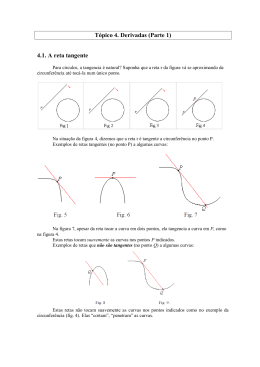
Maria
𝟏∗
𝐂𝐥𝐚𝐫𝐚 ,
𝟐
Ruberlei de Faria
𝟏Faculdade de Engenharia de Bauru– Dep. de Eng. Civil
2Universidade Tecnológica Federal do Paraná– UTFPR− Câmpus Cornélio Procópio
∗[email protected], [email protected]
Introdução
Em diversas esferas de nosso meio, surgem problemas em que são necessárias descrições de
funções a partir do conhecimento prévio de suas taxas de variação (em termos matemáticos,
suas derivadas), isto é, da solução de uma equação diferencial.
Nas últimas décadas vários autores ressaltaram que as derivadas e integrais de ordens
não inteiras são muito satisfatórias na descrição das propriedades de materiais utilizados,
tais como os polímeros. Foi provado que o assim chamado cálculo fracionário acaba por ser
ainda mais útil em certas situações para descrição de modelos e propriedades que o já
conhecido cálculo de ordem inteira.
As derivadas fracionais fornecem um excelente instrumento para as descrições de
propriedades hereditárias e de memória de diversos materiais e processos. Essa é a principal
vantagem das derivadas fracionais quando comparadas com os clássicos modelos de
integração habituais.
No presente trabalho, estudamos o problema do oscilador harmônico simples em
sua versão fracionária e mostramos que sua solução, para diferentes valores da derivada,
refina a solução do oscilador harmônico amortecido, isto é, com a diminuição da ordem da
derivada conseguimos recuperar o efeito de todos os atritos existentes em um sistema real.
Oscilador Harmônico Fracionário
Sabemos que a equação diferencial
na qual m, k, m. são constantes positivas, é a equação diferencial que descreve o
deslocamento (elongação) de um sistema massa-mola com massa m, sujeito a uma força do
tipo Hooke, k, em um meio onde o coeficiente de atrito tem módulo m.
Comportamento Gráfico
Objetivo
O principal motivo de solucionar Equações Diferencias consiste em obter uma
previsibilidade melhor e mais detalhada das consequências do objeto que está sendo
estudado. O cálculo fracionário tem parte de sua importância fundamentada nas derivadas
de ordem não inteira, que refinam o procedimento e trazem uma melhor compreensão e
modelagem de fenômenos naturais, sendo de grande auxílio e importância atualmente.
Note que, a medida que
diminuímos a ordem da
derivada, aumentamos
o amortecimento, o que
mostra que mudando a
ordem da derivada
conseguimos
incorporar, com grande
precisão, os atritos do
sistema.
Derivada Fracionária
Podemos definir, a integral de ordem n da seguinte forma:
Figura 1: Comportamento gráfico da função
Mostramos que o operador integral de ordem n, definido pela equação anterior, pode
ser escrito como um integral simples (convolução de Laplace), da função f(t) com a função
Gel’Fand-Shilov,
, e desta forma definimos a integral fracionária como
Bibliografia
W. E. Boyce and R. C. DiPrima, “Equações Diferenciais Elementares e Problemas de Valores de
Contorno”, Oitava Edição, LTC, Rio de Janeiro, (2006).
[2] R. F. Camargo, “Cálculo Fracionário e Aplicações”, tese de doutorado, IMECC UNICAMP, 2009.
[3] E. C. de Oliveira and J. E. Maiorino, “Introdução aos métodos da Matemática aplicada”, Editora
Unicamp.
[4] [6] H. Guidorizzi, “Um Curso de Cálculo”, Volume 2, 2001.
[1]
Sabe-se que a derivada é o operador inverso à esquerda da integral, no entanto, não
aplicável à todos os casos.
Agradecimentos
Para tanto, Caputo desenvolveu um estudo cuja derivada é o operador inverso à
direita da integral, ou seja, sendo n – 1 < a < n, temos
Neste espaço devemos agradecer o DAMAT pelo financiamento da impressão do
pôster e também os orgão financiadores do trabalho.