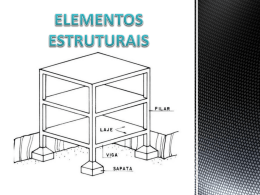
Lajes
Espessuras mínimas conforme NBR 6118, item 13.2.4.1:
— Laje para cobertura: 5cm
— Laje para piso: 7cm
— Laje para passagem de veículos: 12cm
Lajes isoladas
Esquema geral
Lajes isoladas
Engastamento desprezível entre laje e viga
Lajes isoladas
Dimensionamento de laje isolada consiste em
— Determinar a espessura
— Determinar a armadura que ficará no meio do vão
— Determinar a armadura de contorno
Lajes conjugadas
Lajes conjugadas
Corte
Deformação
Esquema estrutural
Lajes conjugadas
Lajes conjugadas
1. Armadura para momento positivo nas lajes
2. Armadura de contorno (construtiva)
3. Armadura para momento negativo (nos apoios)
4. Armadura das vigas (momento positivo)
5. Estribos das vigas (para vencer o cisalhamento das vigas)
6. Porta estribos das vigas
7. Caranguejo (armadura para fixar a armadura negativa)
8. Espaçador (para garantir o recobrimento da armadura)
Lajes conjugadas
Lajes
Geometria
— Armada em uma direção: lado maior > 2 x lado menor
— Armada em duas direções: lado maior ≤ 2 x lado menor
Lajes
Armadas em
uma direção
Lajes
Armadas em
duas direções
Lajes
Armadas em
duas direções
Lajes
Armadas em duas direções
Processo de Marcus
Mx - momento fletor que ocorre no meio do vão. Com Mx e a espessura da laje
será possível calcular a armadura positiva (face inferior) na direção X.
My - idem eixo Y
Xx - momento fletor no apoio na direção X. Só ocorre se há engaste com outra
laje nesse lado e nessa direção. Com Xx e a espessura da laje será possível
calcular a armadura negativa (face superior) na direção X.
Xy - idem eixo Y.
q - carga total que atua na laje (uso e peso próprio)
qx - parcela da carga total que atua na direção X e que será usada para o cálculo
do momento negativo
qy - idem eixo Y.
qx + qy = q
mx e my : coeficiente de cálculo
X e Y : para cada um dos seis casos a direção X deve ser:
— a direção com o maior número de engastes (casos 2, 3 e 6)
— caso haja igualdade de engastes, Ly ≥ Lx (casos 1, 4 e 5)
Lajes
Armadas em duas direções
Caso 1
— Sem engastes
— Direção Y tem Ly≥Lx
Processo de Marcus
Lajes
Armadas em duas direções
Caso 2
— Um engaste
— X é a direção do maior número de engastes
Processo de Marcus
Lajes
Armadas em duas direções
Caso 3
— Dois engastes
— X é a direção do maior número de engastes
Processo de Marcus
Lajes
Armadas em duas direções
Processo de Marcus
Caso 4
— Dois engastes
— Como número de engastes é igual em qualquer direção, então considere Ly≥Lx
Lajes
Armadas em duas direções
Processo de Marcus
Caso 5
— Quatro engastes
— Como número de engastes é igual em qualquer direção, então considere Ly≥Lx
Lajes
Armadas em duas direções
Caso 6
— Três engastes
— X é a direção do maior número de engastes
Processo de Marcus
Lajes
Armadas em duas direções
Processo de Marcus
Passos para a aplicação do processo de Marcus
1. Verificar em qual dos seis casos nos encontramos
2. Orientar os eixos. Nos casos 1, 4 e 5 direção Y tem a maior dimensão. Nos casos 2, 3
e 6, X é obrigatoriamente a direção com maior número de engastes.
3. Cálculo da relação λ = Ly / Lx , que nos permite conhecer nas tabelas os valores de
mx, my e kx.
4. Sabendo mx, my e kx, calculamos
• Mx=q.(Lx²/mx) : momento positivo do meio do vão na direção X
• My=q.(Ly²/my) : momento positivo do meio do vão na direção Y
• qx=kx.q : carga na direção X
• qy=q-qx : carga na direção Y
• Xx= (–qx.Lx²)/A : momento negativo do apoio na direção X; A é uma
constante para cada um dos casos
• Xy= (–qy.Ly²)/B : momento negativo do apoio na direção Y; B é uma
constante para cada um dos casos)