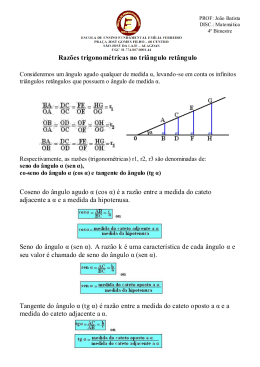
Resumos & Cábulas – Trigonometria 11º Ano
A palavra trigonometria pode justificar-se como tri (três)+ gono (lado) + metria (medida)...De facto na
sua origem pretendia relacionar os lados com os ângulos num triângulo.
Vamos começar por definir algumas dessas relações e para isso
servimo-nos da figura à esquerda.
1) Vamos chamar seno, de um ângulo agudo, ao quociente entre as
medidas do cateto oposto a esse ângulo e a hipotenusa. Assim teremos:
2) Designaremos co-seno, de um ângulo agudo, como sendo o quociente entre o cateto adjacente (cateto
que é um dos lados do ângulo) e a hipotenusa (lado oposto ao ângulo recto). Assim:
3) Chama-se tangente, de um ângulo agudo, ao quociente entre cateto oposto a esse ângulo e o cateto
adjacente. Assim:
Seno, Co-seno e Tangente de uma amplitude qualquer
Consideremos o círculo trigonométrico e o ângulo α .
Define-se seno, co-seno e tangente, de uma amplitude
qualquer, da seguinte forma:
sen a = y (ordenada do ponto P)
cos a = x (abcissa do ponto P)
tg a = y1 (ordenada do ponto B)
9 P é o ponto de intersecção do lado extremidade do ângulo com a circunferência.
9 B é o ponto de intersecção do lado extremidade do ângulo (ou do seu prolongamento, caso o
ângulo se encontre no 2º ou 3º quadrante) com a recta tangente à circunferência em A.
Para todo o α,
Enquadramento do seno e do co-seno
Resumos & Cábulas – Trigonometria 11ºAno www.xkmat.pt.to
Pag.1
Redução ao 1º quadrante
Fórmulas Fundamentais da Trigonometria, a saber:
sen 2 a + cos 2 a = 1
Relação Fundamental da Trigonometria
1
tg a =
tg 2 a + 1 =
cos 2 a
sen 2 a = 1 − cos 2 a
Ângulo
Razão
sen
cos
tg
sen a
cos a
cos 2 a = 1 − sen 2 a
π
π
π
π
6
1
2
4
3
2
2
2
2
2
3
2
1
2
1
3
3
2
3
3
π
3π
2
1
0
-1
0
-1
0
N. D.
0
N.D.
Equações Trigonométricas
Quase todas as equações trigonométricas, quando convenientemente tratadas e transformadas,
podem ser reduzidas a pelo menos uma das três equações seguintes:
sen x = sen a
cos x = cos a
tg x = tg a
Estas são as equações trigonométricas elementares ou equações trigonométricas fundamentais.
Resumos & Cábulas – Trigonometria 11ºAno www.xkmat.pt.to
Pag.2
RESOLUÇÃO DA 1ª EQUAÇÃO FUNDAMENTAL
Ela baseia-se no fato de que, se dois arcos têm o mesmo seno, então os ângulos são suplementares.
Logo, podemos escrever que:
sen x = sen a ⇔ x = a + 2kπ
∨ x = π − a + 2kπ (k ∈ Z )
RESOLUÇÃO DA 2ª EQUAÇÃO FUNDAMENTAL
Se dois arcos têm os mesmos co-senos, então os ângulos são simétricos.
Logo, podemos escrever que:
cos x = cos a
x=
a+
RESOLUÇÃO DA 3ª EQUAÇÃO FUNDAMENTAL
Ela baseia-se no fato de que, se dois arcos têm a mesma tangente, então eles são complementares
ou têm suas extremidades simétricas em relação ao centro do círculo trigonométrico.
Logo, podemos escrever que:
Resumos & Cábulas – Trigonometria 11ºAno www.xkmat.pt.to
Pag.3