ARTUR J O S E GONÇALVES
FAYA
AVALIAÇÃO NEUTRÕNICA DE
"BLANKETS
"
DE
TÓRIO
METÁLICO EM REATORES RÁPIDOS REFRIGERADOS POR GÃS
Orientador:
Prof.
Dr.
Willem
Jan
Dissertação
apresentada
Politécnica
da
São
Paulo
Título
de
São
para
Oosterkamp
a
Universidade
a
Mestre
Paulo,
obtenção
em
1975
Escola
de
do
Engenharia
A Su-Chiang
AGRADBQMENTOS
A o P r o f . D r . Rómulo R i b e i r o P i e r o n i ,
Instituto
realização
de E n e r g i a Atómica p o r t e r p r o p o r c i o n a d o
deste
Superintendente
as
condições
do
para a
estudo.
A o P r o f . E n g . P e d r o B e n t o de C a m a r g o , C o o r d e n a d o r Geral
da C o o r d e n a d o r i a
de E n g e n h a r i a N u c l e a r
A o Prof.
críticas,
sugestões
pelo apoio recebido
Dr. R o b e r t o Y. H u k a i , p e l a o r i e n t a ç ã o
e constante
A o Prof.
incentivo
dos
inicial,
.
Dr. Willem J a n O o s t e r k a m p , meu O r i e n t a d o r ,
sua d e d i c a ç ã o e a u x i l i o n o d e s e n v o l v i m e n t o
ção
.
por
deste estudo e i n t e r p r e t a
-
resultados.
Aos o p e r a d o r e s e a n a l i s t a s
Dados p e l a ajuda p r e s t a d a
S Srta,
do C e n t r o de P r o c e s s a m e n t o de
na e x e c u ç ã o dos p r o g r a m a s .
Creusa Moreira Diniz pelo t r a b a l h o
de
datilogra_
fia.
Aos c o l e g a s
apoio e
interesse
da C o o r d e n a d o r i a
demonstrados.
de E n g e n h a r i a N u c l e a r
pelo
ÍNDICE
1. INTRODUÇÃO
1.2
1
- Estudos
anteriores
4
2. MODELO UTILIZADO
2«1
-
2.2-0
2.3
In
t
7
r*ccduiçâO
o < > . • „ <
o<
« « . « . . o » »
»
»
o
r e a t o r GCFR de 300 MW(e)
- Elementos
3.
2.6
- Administração
de v o l u m e
- Preparação
o
•
7
• 12
12
de c o m b u s t í v e l
15
MÉTODO DE CALCULO
3.1
*
10
2.4 - G e o m e t r i a do GCFR de 300 MW(e)
- Frações
o
8
combustíveis
2.5
•
17
das s e c ç õ e s
de choque
17
3.1.1
- Método do f a t o r de a u t o b l i n d a g e m
17
3.1.2
- Interpolação
22
3.1.3
- Condensação das s e c ç õ e s
3.3 - E r r o s
e incertezas
dos
fatores
de a u t o b l i n d a g e m
de c h o q u e
na a v a l i a ç ã o
26
27
3.3.1
- Método de c a l c u l o .
27
3.3.2
- Constantes n u c l e a r e s . —
31
3.3.3
- Conclusão
34
4 . RESULTADOS
36
4 o 1
4 .2 -
-
Introdução
Consistência
4.2.1
das
„
constantes
36
nucleares
- O r e a t o r GCFR de r e f e r ê n c i a
36
("benchmark")
4 . 2 . 2 - R e s u l t a d o s o b t i d o s na a v a l i a ç ã o do
36
GCFR de
referência
4.3
36
- Avaliação do c o b e r t o r r a d i a l :
4.3.1
Th
vs.
UOg
- E n r i q u e c i m e n t o n o c a r o ç o do r e a t o r e
mento do f a t o r
- Balanceamento
4.3.3
- Produção de material
4.3.4
- Razão de c o n v e r s ã o
4.4 -
Cobertor radial
4.5 - Cobertor r a d i a l
38
de n e u t r o n s
41
fTssil
4 6
interna e distribuição
potênci a
- Produção
comporta-
de m u l t i p l i c a ç ã o
4.3.2
4.3.5
38
de
50
o
de U-232
de
51
Th02
53
de Th com uma ú n i c a f i l e i r a
de
ele-
mentos o . . o . o
57
5. CONCLUSÕES
59
APÊNDICE A - H i p ó t e s e p a r a o c a l c u l o do GCFR de r e f e r ê n c i a
63
APÊNDICE B - S e c ç õ e s de choque e f e t i v a s
de c a p t u r a e f i s s ã o
dos
i s ó t o p o s U-238 e Th-232 em 30 g r u p o s de e n e r g i a
APÊNDICE C - B a l a n c e a m e n t o de n e u t r o n s do GCFR p r o t ó t i p o com cober
t o r de Th em 12 e em 4 g r u p o s de e n e r g i a
APÊNDICE D - Programa C O L L A P S E
APÊNDICE E - R e f e r ê n c i a s
67
A
68
71
RESUMO
Apresenta-se
de u m
" b l a n k e t " de
dos r e f r i g e r a d o s
tálico
pais
e
parâmetros i n t e g r a i s .
metálico
se r e f e r e
Th02
produção
de
com
base
do
rãpj_
t ó r i o me¬
nos v a l o r e s dos p r i n c i
A
E m r e l a ç ã o ao UO
substanciais
material
neutrÔnica
s e r u s a d o em r e a t o r e s
Compara-se o c o m p o r t a m e n t o
proporciona vantagens
a
e s t u d o uma a v a l i a ç ã o
tório metálico a
por gás.
com os de UOg
neste
fTssil.
(ou ThOg)
-
o
tório
principalmente
n o que
1
1 . INTRODUÇÃO
1 . 1 -
Prefacio
0 grande esforço
desenvolvimento
de r e a t o r e s
a t u a l m e n t e d i s p e n d i d o na
rápidos visa,
acima de t u d o ,
pesquisa
e
atender
a
c r e s c e n t e demanda de e n e r g i a de uma m a n e i r a e c o n o m i c a m e n t e v i á v e l .
Rea_
tores
para
nucleares,
de u m modo g e r a l , vem se t o r n a n d o c o m p e t i t i v o s
a g e r a ç ã o de e n e r g i a e l é t r i c a d e v i d o ao b a i x o c u s t o
combustível
em
em r e l a ç ã o
particular,
material
físsil
inesgotável
riam
aos de c o m b u s t í v e i s
tem a p o s s i b i l i d a d e
Reatores
produzir maior
n u c l e a r pode s e r o b t i d a .
apenas por f a t o r e s
econômicos,
m u i t o c a r a a e x t r a ç ã o de u r â n i o e t ó r i o
prias
fosseis.
rial
físsil
(blankets)
i conseguida
nos q u a i s
rápidos,
a regeneração
envolvendo-se
está presente
o caroço
o material
teis,
U-238 e/ou T h - 2 3 2 , são c o n v e r t i d o s
e/ou
U-233, respectivamente
As
fontes
reservas
se torne
como as
, através
(breeding)
(core)
fértil.
em i s ó t o p o s
Os
)
6
U - 2 3 8 ( n , ) U-239 • - »
23 min
Y
de t r a n s m u t a ç õ e s
Th-232(n,Y)Th-233
3
*>
22 min
N -239 — — & >
2,3 d
Pa-23.3
-—»
27,4. d
por
pró-
Pu-239
U- 233
de mate¬
cobertores
isótopos
físseis,
neutrons:
(2)
de
rochas/35/.
Em r e a t o r e s
( 1
,
praticamente
ã medida que se
de o u t r a s
de
rápidos
quantidade
do que consomem. N e s t e c a s o , uma f o n t e
de c o m b u s t í v e l
limitadas
de
de seus c i c l o s
Pu-
induzidas
fér239
por
2
E x i s t e uma
versão f é r t i l - f T s s i l
s é r i e de f a t o r e s
que t o r n a m a t r a t i v a a
r e p r e s e n t a d a p e l o esquema
(2),
a
saber
1. C o n s i d e r a n d o - s e o mesmo c u s t o de e x t r a ç ã o ,
vas
:
as
reser-
de t ó r i o são da mesma ordem de g r a n d e z a das de u r â n i o / 3 5 / .
é o a s p e c t o económico que deve s e r r e s s a l t a d o
a utilização
do t ó r i o em r e a t o r e s
c o n s e r v a ç ã o das r e s e r v a s
nucleares
a q u i , porém,
possibilita,
o
por neutron absorvido
1.]
Tabela
Isótopo
ilustra
1.1 - V a l o r e s
do que
Espectro
p r i n c i p a i s isótopos
fTsseis
Espectro
térmico
rápido
(
FBR )
2,29
2,2
2,3
-
2,4
U-235
2,07
2,0
2,0
-
2,2
Pu-239
2,09
1,9
2,4
Pu-239 e l a d e c r e s c e
4.
material
a
neutrons
U-233
U-233 é p r a t i c a m e n t e
,
o P u - 2 3 9 ou o U - 2 3 5 . A Tabe
( LWR )
3. N m
que
fato.
de e t a p a r a os
2200 m/s
de
de u r â n i o p o r um tempo mais l o n g o / 3 4 / .
( fator eta)
este
Não
a priori
2. Num e s p e c t r o t é r m i c o , o U-233 p r o d u z mais
la
con
espectro térmico,
insensível
-
2,7
a p r o d u ç ã o de n e u t r o n s
i temperatura
pelo
e n q u a n t o p a r a o U-235
e
com o aumento de t e m p e r a t u r a / 3 4 / .
As propriedades
físicas
a p r e s e n t e melhor e s t a b i l i d a d e
d o t ó r i o permitem que
a irradiação
e maiores
este
tempos
3
de e x p o s i ç ã o a r a d i a ç ã o do q u e o u r â n i o / 5 / . E s t a e uma vantagem eco¬
nômica
pois t r a d u z - s e
cação
por unidade
de e n e r g i a
5.
suirá um valor
próximos
em menores
Estudos
entre
30 anos
/23/
tencial
de
/ 1 9 , 3 8 / i n d i c a m q u e o U-233 pos¬
1,5 e 2 v e z e s m a i o r que a q u e l e do P u - 2 3 9
do t ó r i o em r e a t o r e s
para o Brasil
de t ó r i o
cujas
otimistas
proporcionariam
nucleares
(Gas-Cooled £ a s t
s a n t e p a r a os
estimadas
uma s i g n i f i c a t i v a
fonte
de
fatos
são
de
volume
G C
E s t a Í uma a l t e r n a t i v a
inicialmente
propostos
d i ó x i d o de u r â n i o
pela
F R
interes
General
-
Atomics
( U 0 2 ) ou d i ó x i d o de t ó r i o
elementos
combustíveis
metálicos
maior a ser ocupada pelo m a t e r i a l
combinados
no
(
fazem
prever
uma
r e s u l t a m numa
fértil;
maior produção
os
fra
dois
de m a t e r i a l
fís_
cobertor.
Um r e a t o r m o d e l o , p r o j e t a d o p e l a GA, é d e s c r i t o
C a p í t u l o 2. N o C a p í t u l o
3
zado
ao esquema de p r e p a r a ç ã o das c o n s t a n t e s
ares.
po¬
d e s t e e s t u d o é r e a l i z a r uma a v a l i a ç ã o ne_u
Breeder R e a c t o r s ) .
cobertores
or e, além d i s s o ,
sil
de
. E m r e l a ç ã o a e s t e s , o t ó r i o m e t á l i c o p o s s u e uma d e n s i d a d e mai_
Th02)
ção
e
reservas
t r Ô n i c a de u m c o b e r t o r de t ó r i o m e t á l i c o p a r a r e a t o r e s t i p o
, que
nos
divisas.
0 objetivo
(GA)
fabrj_
, p e l o menos.
interesse
de m i n é r i o s
e
produzida.
recentes
A utilização
particular
custos para reprocessamento
, dando-se
Em
ênfase
apresenta-se
o método de c á l c u l o
s e g u i d a , n o C a p í t u l o 4 , são a p r e s e n t a d o s
lores
obtidos
p a r a os p r i n c i p a i s
do-se
os t r ê s m a t e r i a i s
férteis
parâmetros
no
utili¬
e discutidos
neutrônicos,
p a r a uso n o c o b e r t o r :
Th *
nucle_
os va_
considerar
U0„
A
e
4
ThCA.
As
1.2-
conclusões
Estudos
s o b r e e s t e e s t u d o formam o
Capítulo
5.
anteriores
A grande maioria
dos e s t u d o s
encontrados
/l4,19,22,28
,
3 8 / c o n s i d e r a m a u t i l i z a ç ã o de t ó r i o em r e a t o r e s t i p o LMFBR ( L i q u i d
Metal
Fast Breeder Reactor).
são e s c a s s o s
Estudos
semelhantes
para r e a t o r e s
GCFR
/ 9 , 3 0 / e dão Ünfase ao a s p e c t o econômico da u t i l i z a ç ã o
do
tório.
Numa a n t i g a p u b l i c a ç ã o
/ 2 2 / , Loewenstein
daram o c o m p o r t a m e n t o dos c i c l o s P u - 2 3 9 / U - 2 3 8 / P u - 2 3 9
e Okrent
estu¬
e U-233/Th-232
/
U - 2 3 3 * em r e a t o r e s LMFBR. Os a u t o r e s chegaram a r e s u l t a d o s que i n d i c a vam
p a r a o c i c l o do u r â n i o uma r a z ã o de r e g e n e r a ç ã o
a 30%
significativa
.0
ratio)
20
s u p e r i o r a do c i c l o do t ó r i o .
Outros estudos
tor
(breeding
/14,
do c i c l o d o t ó r i o
ciclo
do t ó r i o
permite
2 8 / m o s t r a r a m que a ú n i c a
r e s i d i a no a s p e c t o
coeficientes
de
vantagem
de s e g u r a n ç a d o r e a -
r e a t i v i d a d e mais
negati¬
vos em r e l a ç ã o ao c i c l o do u r â n i o , em r e a t o r e s LMFBR.
* Nesta n o t a ç ã o ,
o primeiro
isótopo é o isótopo
d o m i n a n t e p a r a a g e r a ç ã o de e n e r g i a ;
minante;
sÓtopo
o terceiro
fértil,
é o
central
isótopo
,
fTssil
inicialmente
o segundo e o i s ó t o p o f é r t i l
fTssil
da nome ao
predominantemente
ciclo
.
formado.
pre¬
predo¬
0 i¬
5
Tendo em v i s t a e s t e ú l t i m o
s u g e r i u u m r e a t o r LMFBR no qual
t o i, o c o m b u s t í v e l
U-238
tor
e Pu-239.
. Para e s t e
consistiria
Th0
2
, Leipunski
/20
o c a r o ç o o p e r a r i a num c i c l o m i s t o ,
numa m i s t u r a
seria utilizado
cobertor,
aspecto
Leipunski
dos
isótopos
como m a t e r i a l
encontrou
Th-232,
fértil
uma r a z ã o de
/
is¬
U-233
no cober regeneração
i n f e r i o r em 2 a 3 % ao v a l o r o b t i d o p a r a o r e a t o r o p e r a n d o n o c i c l o
do
urânio.
Lang / 1 9 / usou um modelo a n t i g o de LMFBR p a r a
seus
cálculos.
N a q u e l e modelo os
t a n t o na p a r t e e x t e r n a
Allis-Chalmers
de
de
um
radiais
como na r e g i ã o c e n t r a l
estão
do r e a t o r
presentes
( projeto
da
1964 / 1 5 / ). P a r a u m c o b e r t o r de t ó r i o m e t á l i c o
a ra¬
zão de r e g e n e r a ç ã o
caso
cobertores
efetuar
calculada mostrou-se praticamente
cobertor
igual
a obtida
de U 0 2 .
Wood e D r i s c o l l 7 3 8/ r e a l i z a r a m u m e x t e n s o e s t u d o
a utilização
sistemas
de T h 0 2 em c o b e r t o r e s
( combustível
no
de r e a t o r e s LMFBR.
Consideraram
sobre
tres
na forma de Ó x i d o ) :
(1) Caroço e c o b e r t o r n o c i c l o do
(2) Caroço n o c i c l o d o u r â n i o ,
urânio
c o b e r t o r n o c i c l o do t ó ¬
rio
(3) Caroço e c o b e r t o r n o c i c l o do
0 ultimo sistema mostrou-se
fere
a massa f í s s i l
inferior
n e c e s s á r i a no c a r o ç o ,
(burnup ) media de c o m b u s t í v e l
meiros
fuel
sistemas
management)
aos
no c a r o ç o .
tório.
dois primeiros
cobertor radial.
re
r a z ã o de r e g e n e r a ç ã o e queima
A comparação e n t r e os d o i s pri_
dependeu do esquema de a d m i n i s t r a ç ã o
do
n o que se
de c o m b u s t í v e l
0 ThCL m o s t r o u - s e s u p e r i o r c a s o
(
o
esquema a d o t a d o a d m i t i s s e ,
ao
l o c a m e n t o dos
da f i l e i r a
cente
combustíveis
exterior
(
in-out
fuel
fim de cada c i c l o do r e a t o r ,
shuffle
que ocupam p a r a
o
des_
a fileira
adja_
management).
E m / 9 / O o s t e r k a m p , Faya e Shu e s t u d a r a m o comporta mento de um c o b e r t o r de t ó r i o m e t á l i c o p a r a r e a t o r e s I M B R e
A t r i b u i n d o os
p r e ç o s de U $
GCFR .
10/g e U $
1 6 , 7 / g p a r a os i s ó t o p o s
fís-
seis
Pu-239 e U-233, r e s p e c t i v a m e n t e ,
c o n c l u i r a m que o t ó r i o
metá-
lico
o f e r e c e uma vantagem e c o n ó m i c a a t r a t i v a ,
em r e l a ç ã o
ao
UO
de c e r c a de u m m i l h ã o de d ó l a r e s p o r - a n o , p a r a u m r e a t o r de
»
1000
MW(e).
Nm
e s t u d o mais r e c e n t e / 3 0 /
comportamento n e u t r õ n i c o
bertores
de r e a t o r e s
fletivos
como o b e r i l o
material
fértil
c a r o ç o foi
são
Th0
2
puramente
puramente
re-
c a r b o n o e, também m i s t u r a s
de
refletivo.
0 enriquecimento
de modo a p e r m i t i r uma a l t a t a x a de
s u p e r i o r em r e l a ç ã o ao UU? e T h 0
de m a t e r i a l
que r e a t o r e s
cem b o a s p e r s p e c t i v a s
de r e g e n e r a ç ã o
a serem u s a d o s em c o -
P a r a o GCFR, o t ó r i o m e t á l i c o a p r e s e n t o u u m
, respectivamente)
concluiu
(BeO), n í q u e l ,
com m a t e r i a l
to l i g e i r a m e n t e
p r o d u ç ã o anual
de d i v e r s o s m a t e r i a i s
I M B R e GCFR, i n c l u i n d o m a t e r i a i s
estabelecido
interna.
, Oosterkamp comparou o
físsil
( 8 e
comportameni
n o que se r e f e r e
( 2% m a i o r ) .
puramente
t e n d o em v i s t a os v a l o r e s
. Quanto a m i s t u r a s
conver¬
10% m a i o r em r e l a ç ã o ao UQ
e r a z ã o de r e g e n e r a ç ã o
com c o b e r t o r e s
2
no
de m a t e r i a l
a
2
e
Oosterkamp
r e f l e t i vos não
ofere¬
obtidos para a razão
fértil
com o u t r o s
pura_
mente r e f l e t i vos e s t a s
a p r e s e n t a r a m o mesmo c o m p o r t a m e n t o que o mate¬
rial
Foi
puramente
fértil.
d e s t a c a d a também a vantagem e c o n ó m i c a
se p r o d u z i r U-233 em l u g a r de P u - 2 3 9 .
em
7
20
MODELO UTILIZADO
2.1
-
Introdução
Na última década, estudos
realizados
na Europa e Es¬
t a d o s Unidos m o s t r a r a m que o uso de h é l i o como r e f r i g e r a n t e
tores
rápidos
quido.
Algumas das p r i n c i p a i s
líquido
são
é uma boa a l t e r n a t i v a p a r a a r e f r i g e r a ç ã o
v a n t a g e n s do h é l i o em r e l a ç ã o ao
para o r e a t o r
t a x a s de r e g e n e r a ç ã o e menor e x c e s s o de
de u m p o s s í v e l
não são c o m p r o m e t e d o r a s
de r a d i o a t i v i d a d e
c i a ú n i c a de i m p u r e z a s p r e s e n t e s
interagem
reativida_
A s s i m , as
consequências
para a segurança
do
da u s i ¬
do h é l i o é m u i t o b a i x o e consequên¬
no g á s .
Além d i s s o , os d o i s
fluidos
quimicamente.
(3)
fri g e r a d o p o r h é l i o
Os s e r v i ç o s de m a n u t e n ç ã o de um r e a t o r r á p i d o
são,
relativamente,
i n e r t e e não r a d i o a t i v o ,
o h é l i o não é
dados de uma a t m o s f e r a
(4)
turas
que
v a z a m e n t o e p o s t e r i o r c o n t a t o do h é l i o com o v a p o r
secundário,
na pois o nível
o
operar.
(2) 0 h é l i o é u m gás i n e r t e .
não
lj_
metal
0 h é l i o i n t e r a g e m u i t o pouco com n e u t r o n s ,
i m p l i c a em m a i o r e s
circuito
p o r metal
enumeradas:
(1)
de
p a r a rea_
de f á c i l
execução.
inflamável
Além
.
0 h é l i o não a t r a v e s s a mudança de f a s e nas
.
Inexiste,
bilidades
n o p r o c e s s o de t r a n s f e r ê n c i a
ração do
refrigerante.
de
d i s p e n s a n d o os cui_
i n e r t e p a r a o v a s o de c o n t e n ç ã o
de o p e r a ç ã o de r e a t o r e s
re_
a s s i m , o p r o b l e m a de
de c a l o r d e c o r r e n t e s
tempera
insta¬
da evapo¬
8
P o r seu l a d o , u m
refrigerante
metálico
líquido
apre
s e n t a uma s é r i e de v a n t a g e n s em r e l a ç ã o ao h é l i o e n t r e as q u a i s
des¬
tacam-se:
(1) A e n e r g i a n e c e s s á r i a p a r a bombear o
frigerante
re¬
é menor.
(2) A l t o
coeficiente
de
transferência
O u t r a r a z ã o que l e v o u a e s c o l r í a do
p a r a os c á l c u l o s
ê o interesse
mais p a r t i c u l a r m e n t e ,
tudos
próprio
de r e a t o r e s
do I n s t i t u t o
de
de
calor.
GCFR
como modelo
Energia
Atômica
a C o o r d e n a d o r i a de E n g e n h a r i a N u c l e a r ,
refrigerados
,
em es¬
a gas.
2-2 - 0 R e a t o r GCFR de 300 MW(e)
T r a t a - s e de u m r e a t o r p r o t ó t i p o p r o j e t a d o
ral
Atomic com o o b j e t i v o
de d e m o n s t r a r a v i a b i l i d a d e
p e l a Gene_
da
refrigera¬
ção a gás p a r a r e a t o r e s r á p i d o s , em c o n d i ç ã o de o p e r a ç ã o . A
G A faz
uso do a v a n ç o a d q u i r i d o na t e c n o l o g i a de c o m p o n e n t e s do s i s t e m a
de
refrigeração
do
do HFGR (High T e m p e r a t u r e G a s - C o o l e d R e a c t o r s )
desenvolvimento
tos
combustíveis
a t i n g i d o nos ú l t i m o s
de
de r e a t o r e s LMBR e de F í s i c a de R e a t o r e s
A Fig.
GCFR, i n c l u i n d o - s e
p r e s s ã o de c o n c r e t o
2.1
o reator,
m o s t r a em p e r s p e c t i v a t o d o o
o s i s t e m a de r e f r i g e r a ç ã o
elemeji
Rápidos.
sistema
e vaso
de
pretendido.
0 projeto original
nio
anos p e l a t e c n o l o g i a
e
/ 3 1/ é b a s e a d o n o c i c l o d o u r â -
. E n t r e t a n t o , em e s t u d o s mais r e c e n t e s / 2 7 , 1 1 / a G A tem
to o uso de Óxido de t ó r i o
como m a t e r i a l
fértil
para o
propos_
cobertor
F i g u r a 2.1
- Perspectiva
do GCFR p r o t o t i p o
10
radial.
tral
Abaixo são a p r e s e n t a d o s
os p r i n c i p a i s
do r e a t o r ,
Potência e l é t r i c a bruta,
Potência e l é t r i c a
Eficiência
- Elementos
de
(pellets)
t i p o 316 ( c l a d d i n g )
MW(e)
líquida
304
, MW(e)
300
36%
e uma m i s t u r a
Assim,
a c o l u n a de p a s t i l h a s
que são e m p i l h a d a s
2
e Pü0
dentro
( fuel
rod)
considerando-se
superior),
de t u b o s
constitue-se
de U 0 2 ( c o b e r t o r a x i a l
de 270 v a r e t a s
.
As v a r e t a s
contem somente p a s t i l h a s
de m a t e r i a l
comporta
Neste estudo sugere-se
gonais
de t ó r i o m e t á l i c o
cobertor radial.
canais
perfurados
necessário
inferior).
Shu-Faya,
fértil
por canais
do co¬
e u m elemen¬
prismas
de r e f r i g e r a ç ã o
hexa.
para
o
a e s t e m o s t r a que o número
de
e p e q u e n o - q u a t r o ou c i n c o c a n a i s
Tese de M e s t r a d o ,
A
varetas.
fértil
S.C.,
arranja
de c o m b u s t í v e l
1 cm de d i â m e t r o - de modo que c o n s e g u e - s e uma a l t a f r a ç ã o
de m a t e r i a l
Um
de aço 316 co
, como a l t e r n a t i v a ,
Outro e s t u d o * a s s o c i a d o
de r e f r i g e r a ç ã o
126
,
pastilhas
de c o m b u s t í v e l
m o pode s e r o b s e r v a d o na F i g u r a 2.2
daquela região
consti¬
de U 0 2 m i s t u r a ¬
de prismasA h e x a g o n a i s
to combustível
aço
o s e n t i d o de cima p a r a b a i x o
das em g e o m e t r i a t r i a n g u l a r d e n t r o
radial
de
na
cuj:o c o m p r i m e n t o é a p r ó p r i a
100,4 cm de p a s t i l h a s
do com P u 0 2 e 4 5 , 2 cm de p a s t i l h a s
bertor
fabricados
2
d e n t r o do t u b o c o n s i s t e ém: 4 5 , 2 cm de
de U 0 2 ( c o b e r t o r a x i a l
elemento combustível
de U 0
. U m t u b o d e s t e s p r e e n c h i d o com c o m b u s t í v e l
t u e uma v a r e t a de c o m b u s t í v e l
do r e a t o r .
804
combustíveis
forma de p a s t i l h a s
altura
MW(e)
da c e n t r a l
0 combustível
*
da cen¬
n u c l e a r de 300 MW(e).
Potência térmica
2.3
dados de p r o j e t o
a ser
publicada.
de
volumétrica
FUS
1
S¿S
SN
12
2.4 - G e o m e t r i a do 6CFR de 300 MW(e)
Os e l e m e n t o s
tal
combustíveis
slo dispostos
num a r r a n j o
m a n e i r a que a forma do r e a t o r se a p r o x i m a de u m c i l i n d r o
A Figura 2.3 mostra um corte horizontal
de
quadrado.
do r e a t o r a a l t u r a média do ca
roço.
Para e f e i t o s
de c a l c u l o
por um r e a t o r c i l í n d r i c o . No r e a t o r
d e t e r m i n a d a zona ê m a n t i d o i g u a l
reator real.
2.4
real
"cilindrizado"
foi
simulado -
o volume de de uma
ao volume da zona c o r r e s p o n d e n t e
U m q u a r t o do r e a t o r
com as d i m e n s õ e s
, o reator
"cilindrizado"
representativas
é m o s t r a d o na
do
Figura
do r e a t o r o p e r a n d o a p l e n a
potên¬
cia.
2.5
- Frações
de
volume
0 c a r o ç o do r e a t o r ê d i v i d i d o em q u a t r o zonas com eri riquecimentosdiferentes.
0 objetivo
5 a o b t e n ç ã o de u m p e r f i l
damente p l a n o p a r a a c u r v a de d i s t r i b u i ç ã o
aproxima
de p o t ê n c i a no s e n t i d o
ra¬
dial.
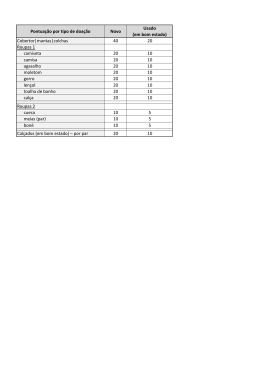
As frações
de volume o c u p a d a s p e l o s
que c o n s t i t u e m o r e a t o r são i n d i c a d a s
T a b e l a 2.2 - F r a ç õ e s
cobertor
na
de volume n o c a r o ç o
Tabela
diversos
materiais
2.2.
(cobertor axial)
e
no
radial
Zona 1
Zona 2
Zona 3
Zona 4
Cobertor
radial
U02(Th02)
Th
Combustível
0,2785
0,2714
0,2705
0,2861
0,4257
0,85
Refrigerante
0,5610
0,5681
0,5691
0,5534
0,4266
0,10
0,1604
0,1605
0,1604
0,1605
0,1477
0,05
Estrutura
e
Encamisamento
ZONE
1
ZONE
Figura 2.3
2
ZONE
{,,_') ZONE
- Seccao h o r i z o n t a l
3
k
7
\W I
do r e a t o r a a l t u r a do
BLANKET
CONTROL
ELEMENT
caroco
115, 2
Ref l e t o r
95,2
z (cm)
Cobertor
axial
Cobertor
50,2-
radial
Zona
I
Zona 2
51,5
Zona
68,5
3 Zona
4
133,4
100,5
85,3
r (cm)
FIG
2.4
-
Dimensões
cilindrizado
de
um
quarto
equivalente
do
ao
reator
CGFR
de
300MW(e)
153,4
15
t
A d e n s i d a d e do c o m b u s t í v e l
no caroço (U0
87% da d e n s i d a d e t e ó r i c a e n o c o b e r t o r r a d i a l , 9 1 % .
e n c a m i s a m e n t o são de aço
Ferro,
+ Pu0 )
2
A estrutura e o
316 SS com a s e g u i n t e c o m p o s i ç ã o
17,5% Cromo, 12,4% N i q u e l , 2,6% M o l i b i d i n i o .
d e s c a r r e g a d o de u m r e a t o r de I g u a l e v e
: 67,5%
A composição
t ó p i c a do p l u t ó n i o usado para a l i m e n t a r o r e a t o r e t í p i c a
tível
e
2
is£
d o combus¬
: Pu-239/Pu-240/Pu-241/
Pu-242 = 5 5 / 2 5 / 1 4 / 6 .
2.6
- A d m i n i s t r a ç ã o de c o m b u s t í v e l
U m t e r ç o dos e l e m e n t o s c o m b u s t í v e i s do c a r o ç o Ó t r o cado a i n t e r v a l o s
a n u a i s , o que c o r r e s p o n d e a 250 d i a s
r a n d o em p l e n a p o t ê n c i a .
Cada e l e m e n t o de c o m b u s t í v e l
p e r m a n e c e no c a r o ç o p o r u m p e r í o d o
de 750 d i a s
m o esquema e s e g u i d o p a r a a p r i m e i r a
do c o b e r t o r r a d i a l .
Existe
razões
r e a t o r perde paulatinamente
controle
são r e t i r a d a s
tituição
anual
físicas
e econômicas
de
seu e x c e s s o
dos e l e m e n t o s
,
0 mes¬
combustíveis
para
a esco -
combustível.
, a medida que o c o m b u s t í v e l
e l e m e n t o s novos ê s u f i c i e n t e p a r a
de c o m b u s t í v e l
de o p e r a ç ã o .
de r e a t i v i d a d e
é queimado, o
e as b a r r a s de
passo a p a s s o para compensar a perda.
de u m t e r ç o
reatividade necessário
, portanto
l i n h a de e l e m e n t o s
l h a de u m c e r t o esquema de a d m i n i s t r a ç ã o
No caroço
do r e a t o r ope_
combustíveis
A subs¬
queimados
por
que o r e a t o r r e t o m e o e x c e s s o :
p a r a sua o p e r a ç ã o p o r 250 d i a s .
Os
de
elementos
p e r m a n e c e n d o no c a r o ç o p o r u m p e r í o d o de 750 d i a s
atin_
gem queimas m é d i a s de 100 MWD/kg, um v a l o r e c o n o m i c a m e n t e a t r a t i v o
is
corresponde,
aproximadamente
, a queima de 10% de t o d o m a t e r i a l
p£
-
16
fissionâvel
p r e s e n t e no e l e m e n t o n o v o .
queima de c o m b u s t í v e l
em r e a t o r e s
de
Em termos
de
comparação,
agua l e v e não u l t r a p a s s a
a
30
MWD/kg.
No cobertor radial
la
GA.
econômico
o esquema e i d ê n t i c o ao p r o p o s t o pe_
V á r i o s esquemas d i f e r e n t e s
detalhado / 2 5 , 3 8 /
Entretanto,
isto
esta
fora
poderiam ser t e s t a d o s
m o s t r a r i a o mais
dos
objetivos
e um
interessante
deste
trabalho.
estudo
entre
eles.
17
3, MÉTODO
DE
CALCULO
3 1 - Preparação das secções de choque
3.1.1
- Método do fator de autobl ir.dagem
Oddo aos valores relativamente baixos de secções de choque da maioria dos materiais par? neutrons rápidos, os efeitos
terogeneidade em reatores rápidos são pequenos.
0 caminho livre
de h e médio
dos neutrons é grande comparado as dimensões das pastilhas de combustí
v e l , distancia entre
varetas de combustível, etc. Em
estudos
paramé
tricôs como este poda-se considerar o reator como composto de zonas h£
mogeneas. Em outros termos, numa região do reator onde a composição se
mantém fixa,
as constantes nueleere?. seo funções da energia de neutron
i n c ddft n t e , e xc 1 us i v amen te.
No método do fator us autobl ir:dagem um conjunto de constantes nucleares
pos de
energia
nucleares»
clear
ra
Data
'is eros r.Ôpicav é compilado num número discreto de gru( 3 0 - 50 ) , a partir de uma biblioteca de
como, por exemplo, o
DF/B-III
constantes
(ENDF para Evaluated
Nu-
File, compilado pelo Brookhaven National Laboratory) . Pa-
efetuar esta compi 1 f.ção e adotada uma certa forma padrão para o es_
pectro de neutron^,
0 espectro padrão deve ser tal que resulte nos me¬
nores
erros p o s s í v e i s
•serão
utilizadas.
pira os cálculos
0 espectro padrão
-p
onde as constantes
(E,) usado como
compiladas
função ponderado
18
ra p a r a
a
compilação
$
e
(E)
dado
por :
= JE
0
para
0 < E <
2,23
MV
(3.1)
=\[E.
A
constante
x
e"
E / X
para
depende d o i s ó t o p o
E > 2,23
físsil
MeV
predominante.
Quando um i s ó t o p o a c h a - s e p r e s e n t e num meio
concentrações,
o c o m p o r t a m e n t o de sua s e c ç ã o de c h o q u e , p o r v e n t u r a
pres.entando r e s s o n â n c i a s ,
meio.
Diz-se
que o
não a f e t a
o e s p e c t r o de n e u t r o n s
isótopo acha-se
"infinitamente
ção de choque m i c r o s c ó p i c a d o i s ó t o p o
ra
a
reação
x
,
no
grupo
• <
s
>
a .
r a
o
grupo
x i
diluído".
j _ , infinitamente
£
dada
(E,T
K
(
E )
sec-
diluído,
pa-
por:
dE
(3.2 )
9
<0o
(
são r e a l i z a d a s
E
)
dE
e n t r e os
limites
de e n e r g i a
das s e c ç õ e s
cia e s t r e i t a .
que
g .
s e c ç ã o de choque p a r a uma ou mais
afeta
do
A
Quando a c o n c e n t r a ç ã o do i s ó t o p o e s i g n i f i c a t i v a
presença
a-
jj^E )
=
/
Ambas as i n t e g r a ç õ e s
g_ ,
g
i
defi nem
em b a i x a s
reações
sobremaneira o espectro
de choque e f e t i v a s
0 fluxo
i
assume a
apresenta
de n e u t r o n s .
e sua
ressonâncias,
Para o
assumida a aproximação
de
sua
cálculo
ressona
A
forma
3» (E )
.
*(E)
Zt(
E)
(3.3
)
1 9
secção de choque macroscópica total do
meio.
As secções ae choque efetivas são então calculadas
atra_
ves
/
3.4 )
J
-
dE
A utilização üà ecuação
ei?
1/
r,:
(3.4)
para o calculo de secções
,ue efetivas implicaria em excessivo tempo de computação. Abagyan/
introduziu o conceito d e
fator d e autoblindagem que ajusta a
secção
de c*'-:,ue do isótopo infinitamente diluído:
s
A dependência de
i reduzida a uma única v a r i á v e l
( background
ã .
4
a
em relação a composição do
.(E,T) , secção
de choque
meio
de
fundo
) . Ê definida p o r :
o !.E.T)
0 1
-
i
E
T
2>4-"«< - >
(
3.6
j * i
ende
N
densidade atômica do isótopo i
secção de choque microscópica total do isótopo
¡NST1TUTO
CE
j
20
Usando-se as equações
(3.6)
e possível
(3.2),
(3.3),
(3.4),
(3.5)
e
e s t a b e l e c e r uma f o r m u l a p a r a o c a l c u l o do f a t o r
de
autoblindagem:
a .(E,T) + o».
>M
E
)
dE
/ V ( E ) .
t
/ axi(E,T)*o(E)
dE
9
„F
:
CIE
* (E.T)
t 1
(
3.7
)
onde
QQ.j
v a l o r medio d e
A equação
(3.7)
autoblindagem para f i s s ã o ,
a .(EJ)
no
Q
grupo
g.
e u s a d a p a r a c a l c u l a r os f a t o r e s
captura e espalhamento.
0 fator
b l i n d a g e m p a r a a s e c ç ã o de choque m i c r o s c ó p i c a t o t a l
de
de
aut£
é d e d u z i d o a se_
gui r.
coeficiente
0
difusão
de d i f u s ã o
D
p r e s e n t e na e q u a ç ã o
de n e u t r o n s e i n v e r s a m e n t e p r o p o r c i o n a l
croscopica
total
de
a s e c ç ã o de choque m a
:
D
3
a
9
J
st(E.T
<f>(E).dE = - i —
)
E9
i
*(E).
dE
I
Ou
v9
c
-
9
I'
4>(E)-dE
r$
1
Et(E)
*(E).dE
(
3.8
)
21
Mas,
(3.9
Substituindo-se
(3.9)
e
(3.3)
em
(3.8)
)
tem - se
dE
a„(E,T)
(
M
De (3.10)
, (3.2)
E
)
3.10
)
dE
e (3.3)
vem
dE
a
t l
(EJ)
oí
C
/
dE
a„(E.T)
+ a?.
E
V )dE
/
i
f
As c o m p i l a ç õ e s
C t ( E , T ) * ( E ) dE
de s e c ç õ e s
0
de choque b a s e a d a s
(3.11
neste
)
método
22
apresentam
ou s e i s
RA
geralmente
valores
valores
de
tabelas
e
a
a
tres
intermediários
tores
tabelados.
t o da
Secção
dos
fatores
f*.
calculados
ou q u a t r o v a l o r e s
faz-se
necessária
de
0 esquema de i n t e r p o l a ç ã o
QUE
ressonâncias
TAMBÉM»
dependente
CAMENTE
tanto,
MAS,
dos
fa-
u s a d o n e s t e e s t u d o e obje_
3.1.2.
APRESENTEM
NEUTRONS
cinco
temperatura.
uma i n t e r p o l a ç ã o
D e v e - s e n o t a r que o m i t o d o e a p l i c a d o
TOPOS
para
os f a t o r e s
AQUELES
PARA
CUJA
ALGUNS
TIPOS
NÃO
DE
a iso
SOMENTE
interações
COM
s e c ç ã o de choque i uma função
da e n e r g i a do n e u t r o n
incidente.
de a u t o b l i n d a g e m são i g u a i s
NESTE
FRA-
CASO,
ENTRE¬
ou m u i t o p r ó x i m o s
a uni¬
DADE .
3.1.2
- Interpolação
Esta
dos
fatores
de
Secção t r a t a
autoblindagem
da i n t e r p o l a ç ã o
b l i n d a g e m p a r a o c a s o d o v a l o r c a l c u l a d o de
consecutivos
VALORES
será
CONSIDERADA
UMA
sõtopos p r e s e n t e s ,
,
MISTURA
a
.
, SÃO
O
que
situar-se
a
Q
NORMALMENTE
ACONTECE.
homogênea de i s ó t o p o s ,
de a u t o
,
DADAS
A
s e c ç ã o de choque
fórmulas
PELAS
DE
total
dois
Para
isto
na qual
BREIT
,
, E
- WIGNER
/ 8 /
-
entre
um
i_ , a p r e s e n t a uma r e s s o n â n c i a de a b s o r ç ã o
ã ressonância
PRÓXIMO
CÃO
TABELADOS,
dos f a t o r e s
A
DOS
i-
isolada.
DE
ABSOR
:
ai
VA
k
2
(E -
2
E ) +(r/2)'
0
+
k
+
4TTR
(E - E )
Q
2
+
(r/2)
2
(3.12)
23
o.
lüJ l
(E - E . ) +
= -4 —
-(3.13
z
k
(r/2
)
)2
onde,
k
numero de
onda do n e u t r ó n nas c o o r d e n a d a s
centro-de-massa
do s i s t e m a
fator e s t a t í s t i c o
de
2J + 1
do
neutrón-núcleo;
"spin"
:
.
2(21 + 1 )
J
número q u â n t i c o de " s p i n "
tron-núcleo
alvo
número q u â n t i c o de " s p i n "
E
e n e r g i a do neutrón
e n e r g i a na qual
Q
(nej¿
);
I
E
do n ú c l e o composto
do n ú c l e o a l v o
;
incidente;
a s e c ç ã o de choque de a b s o r ç ã o
i
máxi ma;
r
n
, F
y
p
, R
a r
A
m e
A
r o s
do n e u t r ó n ,
R
do
núcleo
Usando-se
as
definições
h
-
Z
=
t
p
integral
de
=
: l a r g u r a de
Vai
N.a,,
4TTR
V
2
+ N.Ü.,
,
oi
ressonância
nivel
radiativa e total , respectivamente
raio
a,,
a
de r e s s o n â n c i a
pi
, I
;
. pode
ser
calculada
por
;
24
du
N
o
Definindo-se
(3.14
)
(3,15
)
t
ainda
o.
6 »
m
0 s
p
onde
o
m
e
o
valor
máximo
21
SJbÇÍ
Se o isótopo i
to b a i x a s
na m i s t u r a
de
obtém
+ e - r
estiver
» e >>
1 - r
)
presente em concentrações
, a equação
1 = 1
m
«o
Dividindo-se
(
-se
( 3.15 ) se
mul-
reduz
a
(3.16
)
y
3.1§)
por
(
3.16
)
(S + 1 - r )
o
• +
a
(3>"
01
°o1 +
b
JUSTÍTUTO
}
25
onde
b
=
do
secutivãmente.
A
0
e
e
0
•
b_
v a
o r d e
A
de
os v a l o r e s
calcular
a
f
A
O
Q
não
Q
*~ e a
e
a
a
equação
_a
p r a t i c a m e n t e o mesmo em r e l a ç ã o
b - b
k
k
b"
=
=
(3.17)
k
+
a
b_
.
Q
corA
tal
(3.17
que
)
,
=
k
(3.18)
k ;
obtem-se
( 1 , , £
k +1>
-(3.19
0
f
l
a
dizer
£
1
e (3.18)
O' '
poten-
Pode-se
Uma boa a p r o x i m a ç ã o
a Jl-fh - o , k + 1
b
a
, s e c ç ã o de choque de e s p a l h a m e n t o
, e c o n s t a n t e na r e s s o n â n c i a e em suas v i z i n h a n ç a s .
De
autoblin-
, tabelados
Q
Aado p A
tabelados.
do f a t o r de
correspondente
®
a
desconhecidos.
0 v a l o r de
cial
+ -¡
respectivamente
Deseja-se
°ok < o < o k + 1
a_
)
' 3.17) dã* origem a u m a l g o r i t m o de i n t e r p o -
f
dagem c o r r e s p o n d e n t e s
sendo
r
f a t o r de a u t o b l i n d a g e m p a r a v a l o r e s
Sejam
a
1 -
m
A equação
lação
x(
+ <>
~
f
k = k + 1 =k
'kl
<°o,k
-
b
)
"
°ok
3
< °
2 0
>
)
26
3.1.3
- Condensação das s e c ç õ e s
de choque
T e n d o - s e o b t i d o as s e c ç õ e s de choque e f e t i v a s
de e n e r g i a ,
pos
é r e a l i z a d o um c á l c u l o d o r e a t o r m o d e l o , a t r a v é s
programa de d i f u s ã o CITATION
ciais
. 0 programa fornece
trons
em cada
( Secção 3 . 2 . ) , p a r a as c o n d i ç õ e s
como u m dos r e s u l t a d o s
zona do r e a t o r .
de e n e r g i a
mo
de choque de 30 p a r a
de e n e r g i a
de s e c ç õ e s de c h o q u e .
recomendado p a r a e s t u d o s
e s t e , t e n d o - s e em v i s t a o compromisso e n t r e
Quatro
do
ini_
neu_
como
( p r o g r a m a COLLAPSE - A p ê n d i c e D ), com cada
do r e a t o r p o s s u i n d o seu c o n j u n t o
número de g r u p o s
o e s p e c t r o de
Este espectro é então u t i l i z a d o
função p o n d e r a d o r a p a r a c o n d e n s a r as s e c ç õ e s
grupos
em 30 gru
é
4
zona
um
paramétricos
c£
p r e c i s ã o e tempo
de
computação / 3 1 / .
A T a b e l a 3.1 d e f i n e
gia
que
os g r u p o s
s e g u n d o a f a i x a de e n e r -
ocupam.
T a b e l a 3.1
G
r
u
p
o
- Definição
dos g r u p o s
de e n e r g i a
Limite superior
, eV
1
1,00
x
10
7
2
8,21
x
10
5
3
6,74
x
10
4
4
5,53
x
IO
3
27
3.2
-
Programa
utilizado
0 p r o g r a m a CITATION / I O / , e s c r i t o em l i n g u a g e m FORTRAN
IV
, tem
neutrons
pais
por objetivo
r e s o l v e r problemas
na r e p r e s e n t a ç ã o
caractensticas
(1)
por diferenças
destacam-se
possibilidade
da t e o r i a de d i f u s ã o
finitas.
Entre
de
suas
princi_
de a t e
tris
:
de
r e s o l v e r problemas
dimensões;
(2)
c a l c u l o do c o m p o r t a m e n t o t e m p o r a l
(3)
vários
esquemas p o s s í v e i s
do
reator;
para a administração
de
combustível.
3.3
3
-
-3.1
Erros
e incertezas
- Método de
na
avaliação
calculo
0 método do f a t o r de a u t o b l i n d a g e m t e m - s e r e v e l a d o
técnica
simples
Resultados
e rápida
obtidos
p a r a a c o m p i l a ç ã o de c o n s t a n t e s
/l7,21/.
ache p r e s e n t e um i s ó t o p o com r e s s o n â n c i a s
a hipótese
E (u)
t
nucleares.
p e l a a p l i c a ç ã o d e s t e método concordam com os p r o -
d u z i d o s p o r t é c n i c a s mais s o f i s t i c a d a s
absorção,
uma
de d e n s i d a d e
<j)(u) ~
Num meio em que
em sua s e c ç ã o de choque
de c o l i s ã o
constante
se
de
, isto é ,
constante
e x i g e a c o n d i ç ã o de que a p e r d a média de e n e r g i a do n e u t r o n p o r coli_
são
deva s e r m u i t o m a i o r que a 1 a r g u r a t o t a l
de-se e x p r e s s a r matematicamente
de
/5/
( 1
- a.)
E0
» r
esta
condição
da r e s s o n â n c i a
através
da
r.
Po-
desigualda¬
28
onde E
Q
£ a energia em que ocorre o máximo da ressonância
a =
largura da ressonância e
A
2
[(A-l)/(A+1)] ,
, r £
a
sendo A o numero de
massa do isótopo ressonante. Para isótopos férteis
(que predominam
no reator) esta condição £ satisfatória na faixa resolvida onde
as
ressonâncias são estreitas e suficientemente espaçadas. Em energias
mais altas aparece o problema de sobreposição de ressonâncias agravado pelo efeito Doppler. Para isótopos ffsseis o problema acentuase pois o espaçamento entre ressonâncias £, em m e d i a , muito
Este fenômeno, contudo
choque através
menor.
, £ considerado na preparação das secções de
do programa ETOX-III.
De um modo geral a aproximação de densidade de coli
são constante £ satisfatória para reatores GCFR pois estes possuem
espectros de neutrons mais duro do que outros reatores o que dimi nue a influência das ressonâncias.
Um problema pode ocorrer com o método do fator
autoblindagem quando da definição de o
.
Esta pode tornar-se ambi-
o
gua se mais de um isótopo espalhador ressonante esta presente
meio.
de
no
Isto não foi considerado no estudo pois implicaria apenas
em
modificar ligeiramente algumas secções de choque efetivas de um
ou
dois
grupos dos 30 grupos de energia iniciais. Sua influência
nos
parâmetros integrais, portanto, seria desprezível. Esta ambiguidade
oode ser contornada se para o cálculo de a
so iterativo simples
/l7/:
v+l
>
+ f
onde
v
£ o
for escolhido um proces
índice da
iteração.
29
O esquema de i n t e r p o l a ç ã o
tabelados
em / 1 6 / a p r e s e n t o u r e s u l t a d o s
dos f a t o r e s
concordantes
p o s t o p o r R. B . Kidman / 1 8 / , p u r a m e n t e m a t e m á t i c o .
s e n t a os v a l o r e s
dos f a t o r e s
da esquema de i n t e r p o l a ç ã o ,
de
interpolados
autoblindagem
com o esquema pro
A Tabela
em função
de a
ra do U-238 na f a i x a de e n e r g i a
25 KeV a 41
apre
segundo ca_
aí
p a r a a S e c ç ã o de choque t o t a l
3.2
e de
captu-
KeV.
0 método u s a d o p a r a c o n d e n s a r as s e c ç õ e s
de choque
de
30 p a r a 4 g r u p o s de e n e r g i a b a s e i a - s e numa s u g e s t ã o a p r e s e n t a d a em
/
2/.
-
0 uso de d i f e r e n t e s
nha de e l e m e n t o s
de S e c ç õ e s
do c o b e r t o r r a d i a l ,
de d e p e n d ê n c i a e s p a c i a l
corre
conjuntos
procura
nesta região.
da pouca s e n s i b i l i d a d e
r e l a ç ã o ao número de g r u p o s
de choque p a r a cada li
l e v a r em c o n t a os
Uma g r a n d e vantagem do método de_
dos r e s u l t a d o s
do c á l c u l o de d i f u s ã o
de e n e r g i a u t i l i z a d o s .
culo
d e s t e t i p o em 12 g r u p o s
tipo
e n v o l t o em c o b e r t o r de t ó r i o
de e n e r g i a ,
tados
considerando o reator
cál-
prot£
metálico.
obtidos
Comparando-se com os r e s u l t a d o s
para
apresen-
na S e c ç ã o 4 . 3 , o b t i d o s a t r a v é s d e u m c á l c u l o em 4 g r u p o s
energia
res
em
Realizou-se um
A p r e s e n t a - s e n o A p ê n d i c e C os r e s u l t a d o s
o b a l a n c e a m e n t o de n e u t r o n s .
efeitos
que
, nota-se
que as d i s c r e p â n c i a s
1% p a r a as t a x a s
0 efeito
não foi
são b a s t a n t e s
de r e a ç ã o de i s ó t o p o s
de c a n a l i z a ç ã o
elemento combustível
se t r a t a r de h é l i o
fisseis
de n e u t r o n s
considerado. No r e a t o r p r o t ó t i p o cerca d e
pequenas,
e
(neutron
, pouco i n t e r a g e com o s
neutrons
meno-
férteis.
streaming)
45% d o volume
d o c a r o ç o ê ocupado p e l o r e f r i g e r a n t e
de
que,
do
por
podendo s e r consi_
30
derado
um
"vazio"
p a r a os mesmos.
c a r o ç o devem s e r somados
elementos
combustíveis
Além d i s s o ,
12% do volume
p a r a l e v a r e m c o n t a os i n t e r s t í c i o s
e espaços
a serem o c u p a d o s p o r b a r r a s
do
entre
de cori
t r o l e . P o r t a n t o , 57% do volume do c a r o ç o £ o c u p a d o p o r c a n a i s que se
estendem no s e n t i d o
não i n t e r a g e m .
te,
Tabela
dentro
sua fuga
de m u l t i p l i c a ç ã o
os n e u t r o n s
de
praticamente
mais f a c i l m e n -
d o c a r o ç o e, c o n s e q u e n t e m e n t e ,
diminuindo o
efetivo.
3.2 - Comparação de d o i s
fator
esquemas
de i n t e r p o l a ç ã o
para
o
autoblindagem
Ref.718/
1
dos q u a i s
Os neutrons podem a s s i m difundirem-se
aumentando
fator
axial
este
estudo
Ref./18/ Este
estudo
0,904
0,904
0,874
0,874
2
0,911
0,910
0,880
0,879
6
0,930
0,927
0,898
0,897
10 ( t a b e l a d o )
0,943
0,943
0,911
0,911
20
0,960
0,959
0,933
0,932
60
0,982
0,981
0,965
0,965
100 ( t a b e l a d o )
0,988
0,988
0,976
0,976
(tabelado)
E s t e fenômeno ê, p o r n a t u r e z a ,
de n e u t r o n s ,
e, como t a l „ r e q u e r u m t r a t a m e n t o
da t e o r i a d e t r a n s p o r t e .
de
, axial
difusão
Pellaud /31 /
fluência
tivo,
e radial,
3.3.2
sobre parâmetros
-
Constantes
direcionais
e empregados
integrais,
são o b t i d o s
posteriormente
Resultados
como f a t o r
nucleares
no
eV
10 M V
geralmente.
de r e a t o r e s
rápidos
constantes
nucleares
felizmente,
não £ a r e g r a
Para
destes
Portanto,
por
sua iin
d e m u l t i p l i c a ç ã o efe_
é pequena,
de cada m e d i d a .
tivos
comuns d e s t e s
reatores
A faixa
se e s t e n d e
a previsão
de
A
de
100
das p r o p r i e d a d e s
fí
das
e m função da e n e r g i a o q u e , in¬
geral.
isótopos
diferentes
individual
rápidos.
importar
depende de u m c o n h e c i m e n t o d e t a l h a d o
microscópicas
alguns
de a u t o r e s
para medidas
cálcu-
obtidos
s ã o a t u a l m e n t e a mais
no c á l c u l o de r e a t o r e s
coberta pelo espectro
mais
para
VL
energias
perimentais
cálculo
nucleares
causa de i n c e r t e z a s
a
através
mostram q u e , a o l e v a r - s e em c o n t a e s t e e f e i t o ,
As c o n s t a n t e s
ção
de d i f u s ã o
do r e a t o r homogeneizado.
c o r r e ç õ e s menores que
sicas
calculacionai
t a x a d e c o n v e r s ã o d o c a r o ç o e t a x a de r e g e n e r a ç ã o ,
com
te
transporte
Basicamente ê r e a l i z a d o um
de c é l u l a d o r e a t o r onde os p a r â m e t r o s
cada d i r e ç ã o
de
t é c n i c a de p r o b a b i l i d a d e s
A
de c o l i s ã o p o d e r i a s e r u t i l i z a d a .
lo
um efeito
a discrepância
e n t r e m e d i d a s ex¬
chega a s e r m a i o r que a
A T a b e l a 3.3 i l u s t r a e s t e f i t o .
problemas
relativas.
é a inconsistência
Medidas
absolutas
incerteza
U m dos rrp_
na n o r m a l i z a -
são b a s t a n t e s
difíceis
p r i n c i p a l m e n t e as de s e c ç õ e s de choque de c a p t u r a e fissão de isõto-
33
pos
d e número a t ô m i c o e l e v a d o .
N o r m a l m e n t e e s t a s c o n s t a n t e s são m e d i -
d a s em r e l a ç ã o a uma s e c ç ã o d e choque p a d r ã o .
t e s usam p a d r õ e s d i f e r e n t e s e s e ,
drões possuem incertezas
crepâncias e n t r e
os
alem d i s s o ,
Se e x p e r i ê n c i a s
a s s e c ç õ e s d e choque*'pa-
s i g n i f i c a n t e s , i c l a r o que haverá grandes
v a l o r e s de cada e x p e r i ê n c i a . Uma d a s ' m e d i d a s
d a s como p a d r ã o e a s e c ç ã o d e choque de f i s s ã o d o U - 2 3 5 .
tes
/36,37/
deste padrão revelaram d i s c r e p â n c i a s
para energias
diferen-
dijs
toma
Medidas
receia
e n t r e , si de a t é
15 %
s u p e r i o r e s a 100 KeV. Outra causa d e e r r o s mais s é r i o s
p o r s e r de d e t e ç ã o d i f í c i l ,
,
provem de e r r o s s i s t e m á t i c o s c o m e t i d o s nas
experiências.
T a b e l a 3.3 - V á r i a s m e d i d a s de s e c ç õ e s de choque
U-238 p a r a
a
um n e u t r o n d e
( n , Y ) , mb
de
captura
30 KeV
Autores
(referëncias
em / 7 /
470 ± 38
de S a u s s u r e ,
473 ± 74
Gibbons
479 ± 14
Men l o v e ,
467 ± 18
Pönitz
549 ± 55
Mod i n , Gibbons , Posma
373 ± 77
Hanna,
420 ± 30
Moxon
A T a b e l a 3.4 e x t r a í d a da
tezas
nas p r i n c i p a i s
secções
de
do
et
Weston et
)
al.
al.
Pönitz
Rose
referência
/12/ lista
choque dos i s ó t o p o s
as
incerA
U-238 e P u - 2 3 9
.
33
T a b e l a 3.4 - I n c e r t e z a s
nas secções
de choque dos i s ó t o p o s
U-238
e
Pu-239
Dado
Nuclear
E n e r g i a do n e u t r o n
incerteza
%
incidente
a
100 KeV
10
>
100 KeV
10
a
1
MV
15
>
1
MV
20
>
T
MV
6
>
1
MV
3
0,1
a
20
KeV
10
20
a
300 KeV
10
>
300 KeV
6
0,2
a
20
KeV
20
20
a
80
KeV
20
>
80
KeV
20
Pu-239 v
>
0,1
KeV
2
Pu-239
>
10
KeV
40
U-238
U-238
o(n,j)
1
o(n,n')
U-238 a ( n , f
0,1
)
U-238 v
Pu-239
Pu-239
a(n,f)
0(n,j)
o(n,n')
Em v i s t a
das d i s c r e p â n c i a s
t a d a em r e l a ç ã o
a constantes
cos a v a l i a d o r e s .
A função
didas n u c l e a r e s
informação
obtidas
experimental
das e, f i n a l m e n t e
1i a d a s .
nucleares
destes
experimentais
foi
a politica
a de c r i a r g r u p o s
ado
de fTsi
-
g r u p o s £ r e u n i r o m a i o r número de me¬
por f í s i c o s
experimentais
disponível
, julgar
p r o d u z i r uma b i b l i o t e c a
de
baseando-se
a confiabilidade
constantes
em
toda
das medi¬
nucleares
ava-
34
Os dados a v a l i a d o s s ã o t e s t a d o s
parâmetros
integrais
Para v e r i f i c a r
de
realizados
a precisão
diversas geometrias,
a t r a v é s de m e d i d a s
em e x p e r i e n c i a s
das a v a l i a ç õ e s
composições
são
de m o n t a g e n s
criticas.
usadas montagens
e distribuições
de
espectrais
críticas
de neu¬
trons.
3.3.3
-
Conclusão
Os métodos de c a l c u l o e m p r e g a d o s p a r a a p r e v i s ã o
propriedades
físicas
senvolvimento tal
de r e a t o r e s
certezas
neutrônico
que os e r r o s
dados n u c l e a r e s .
podem s e r
são m u i t o s e n s í v e i s
captura,
devido a defeitos
Entretanto,
de r e a t o r e s
São c o n s t a n t e s
na
teoria
p o r i ni
calculacionais
a previsão
do
mais
comportamento
r á p i d o s " , onde os e f e i t o s
e avaliação neutrõnica
a incertezas
m e d i d a s mais p r e c i s a s
fissão
u m de¬
introduzidos
técnicas
para
anos
de h e t e ¬
importantes.
0 projeto
cessarias
cometidos
devem s e r d e s e n v o l v i d a s
de c o b e r t o r e s
rogeneidade
tem a t i n g i d o nos ú l t i m o s
t o r n a r a m - s e m u i t o menores que os e r r o s
nos
sofisticadas
de r e a t o r e s
de
e espalhamento
fundamentais
de r e a t o r e s
nas c o n s t a n t e s n u c l e a r e s .
de s e c ç õ e s
i nelastico
rápidos
Fazem-se ne_
de choque m i c r o s c ó p i c a s
de i s ó t o p o s
para a determinação
-
físseis
de
e férteis .
do c o m p o r t a m e n t o do rea
tor.
Finalmente,
incertezas
flexo
das
nos p r i n c i p a i s
incertezas
nas
a T a b e l a 3.5
a p r e s e n t a uma e s t i m a t i v a
parâmetros
de r e a t o r e s
constantes
nucleares.
rápidos
das
712/ como re¬
35
Tabela 3.5 - Incerteza nos principais parâmetros
físicos de reato
res rápidos devido a incertezas nos dados nucleares,,
Parâmetros
Massa físsil n o caroço,
(Pu-239
+
Incerteza
±
%
Pu-241)
8
Taxa de regeneração,
±
Coeficiente
±
de Doppler,
0,10
%
20
Reatividade de barras de controle, ±
Densidade de potência máxima
Densidade
de potência media
%
,
± %
no
caroço
15
5
36
4
.
RESULTADOS
4=1 - Introdução
objetivo deste Capítulo e apresentar e discutir o s
0
res
obtidos
todo d e
liação
para os principais parâmetros neutronicos pela aplicação do m e
calculo descrito n o Capítulo 3.
da
consistência
p o r outros
co
dos
dois
tipos
e
4.2
cuja
-
4.2.1
de
faz
sugerir
tonsütênxia
- 0 reator
GCFR
um
una
ropa
calculo
v e r i f i c a ç ã o
e
nos
importantes
4.2.2
Estados
Unidos.
A
de
tório
de
l a b o r a t ó r i o s
h i p o t é t i c o
das
cuja
constantes
G A e s p e c i f i c o u
enviando-os
o s resultados
A
para
e ThQ,.
d emenores
U m
dimen-
f i n a l i d a d e
nucleares
os
dados
para
usadas
n a Eu -
necessários
para diversos
obtidos
permj_
foi
para
l a b o r a t ó r i o s
o sparâmetros
o
inmais
comparação.
Tabela 4.1
estrangeiros
metálico
UO
obtidos
("benchmark")
- Resultados obtidos n a avaliação do G C F R
A
com o s
nucleares
reator
( Apêndice A )
fins
usadas
com as
Capítulo.
de referência
e s o l i c i t a n d o
para
o
d a c o n s i s t ê n c i a
d o reator
t e r n a c i o n a i s
cobertor
d e um
são c o m p a r a d o s
em consideração pela G A ,
constantes
Trata-se
tir
O s resultados
completa
das
utilizadas
Em seguida e avaliado um cobertor de tóYio m e t a l j _
cobertores
avaliação
ava-
Inicialmente, ê realizada uma
constantes nucleares
reator modelo.
resultados
sõe s
das
laboratórios.
para o
outros
valo-
7 2 9 / inclue os
e p o r este estudo.
de referência
resultados
obtidos
0 método de c á l c u l o
por
segue
vários
o
Tabela 4 = 1
-
Resumo
dos
principais
resultados
para
Parâmetros
CA
CEA
IEA
UK
CAD-3
ENDF/B-III
0,9878
0,9910
0,9966
0,9986
0,9815
0,720
0,715
0,705
0,705
0,717
,238
0,256
0,266
0,239
0,263
0,261
af-238
0,048
0,049
0,046
0,047
0,045
V
0,310
0,441
0,385
0,425
0,392
1,735
1,791
1,665
1,790
1,763
1,43
1,44
1,43
1,45
1,46
316
344
330
325
328
Razão de c o n v e r s ã o
k
interna
Secções de choque m e d i a s no c a r o ç o ,
2
3
9
of-239
k
=
P r o d u ç ã o de P u ,
FD-4
barn
1,0
regeneração
OBSERVAÇÃO:
referencia
ENDF/B-III
nucleares
F a t o r de m u l t i p l i c a ç ã o ,
Razão de
de
KFKINR
de c o n s t a n t e s
Ajuste para
GCFR
Laboratórios
CFK
Fontes
o
kg/ano
CJK
CEA
GA
UK
:
:
:
:
G e s e l l s c h a f t für K e r n f o r s c h u n g
Karlsruhe
Comissariat
A L ' E n e r g i e Atomique
General Atomic
Winfrith,
Inglaterra
38
r.ssrno
p o
esquema t r a ç a d o no C a p í t u l o
3 - apenas
o numero e s p e c i f i c a d o
de gru_
s d e e n e r g i a , s e t e , e m a i o r . N o t e - s e a s d i f e r e n t e s b i b l i o t e c a s d e cons_
t a n t e s nucleares usadas p o r
t e nos v a l o r e s
do r e a t o r ,
de secções
cada l a b o r a t ó r i o .
d e choque d e c a p t u r a e f i s s ã o ,
tipli c a ç ã o
Entretanto,
, razão
p a r a os p a r â m e t r o s
d e regeneração
são p e q u e n o s , menores que
e
razão
de
caroço
chegam a s e r
integrais
como f a t o r
conversão
interna
: Th
UC
de muj_
desvios
os
2%.
4 . 3 - A v a l i a ç ã o n e u t r o n i c a do c o b e r t o r r a d i a l
- Enriquecimento
notoriamen¬
medias no
p a r a os i s ó t o p o s PU-239 e U - 2 3 8 . A s d i s c r e p â n c i a s
consideráveis.
4.3.1
Isto se reflete
vs.
A
n o c a r o ç o do r e a t o r e c o m p o r t a m e n t o do f a t o r
de
multiplicação
A variação
sultado
mento
to
de
da
dois
concentração
barras
de
material
destas
barras
trons
por elas
rial
físsil.
vidindo-se
tor
de
fenômenos
dos
de r e a t i v i d a d e
: o consumo de c o m b u s t í v e l
produtos
absorvedor,
as
de f i s s ã o
. Para
como o B - 1 0 ,
No
absorvidos
programa
estão
perdidos
de d i f u s ã o
este
o numero médio de n e u t r o n s
mui t i p l i c a ç ã o
do
sistema
ao
, k
A
£
presença
de p r o d u z i r
levado
por f i s s ã o
neu_
mate_
em c o n t a
, v
, pelo
di¬
fa
.
usados
, embora b a s e a d o s nos dados
, a p r e s e n t a m l i g e i r a s v a r i a ç õ e s e m r e l a ç ã o a q u e l e s . Foram o b s e r v a d a s
hipóteses:
au
efei-
compensar e s t e
do s i s t e m a p o i s
invés
fenômeno
produzidos
e o consequente
são u s a d a s .
£ d a n o s a p a r a a e c o n o m i a de n e u t r o n s
Os enriquecimentos
G A
d u r a n t e o c i c l o d o r e a t o r £ re¬
da
du
39
1) O
f a t o r de m u l t i p l i c a ç ã o
perior
d o r e a t o r deve s e r sempre
a u n i d a d e n o c i c l o de
equilíbrio.
2) P a r a os d o i s s i s t e m a s em e s t u d o , Th e UOA, o f a t o r
multiplicação
d o c i c l o de
deve s e r a p r o x i m a d a m e n t e
dia
fim
p a r a que o rea¬
A s e g u n d a i m p l i c a numa mesma margem de seg_u
r a n ç a p a r a os c a s o s em e s t u d o .
realizadas
o mesmo no
de
equilíbrio.
A primeira h i p ó t e s e £ condição n e c e s s á r i a
t o r m a n t e n h a - s e em o p e r a ç ã o .
su
A s c o m p a r a ç õ e s e n t r e os p a r â m e t r o s
na m e t a d e do c i c l o de
equilíbrio
objetivando-se
são
t o m a r a mi
dos mesmos .
Na Tabela
dos nas zonas
mostra
o
do c a r o ç o
4.2
apresenta-se
, p a r a cada t i p o de c o b e r t o r r a d i a l .
comportamento temporal
tema.
Dois
resultados
dial
de t ó r i o m e t á l i c o
os e n r i q u e c i m e n t o s
n a Secção
A F i g u r a 4.1
do f a t o r de m u l t i p l i c a ç ã o p a r a cada sis_
interessantes
podem s e r o b s e r v a d o s :
requer maior e n r i q u e c i m e n t o
e a p r e s e n t a m a i o r queda de r e a t i v i d a d e n o c i c l o
discutidos
emprega¬
o c o b e r t o r ra_
no caroço do
de e q u i l í b r i o .
reator
Ambos
são
4.3.2.
T a b e l a 4.2 - E n r i q u e c i m e n t o s
utilizados
Zona
Th
nas z o n a s do c a r o ç o do r e a t o r ,
Cobertor
'J0
radial
2
Th0
2
Zona
I
13,3
12,8
13,1
Zona
2
16,0
15,4
15,7
Zona
3
18,3
17,6
Zona
4
22,0
21 ,2
18,0
21
,7
%
1
250
I
500
I
750
—i
1
1
250
Fig.4.1 - Comportamento
de
multiplicação
7 50
500
temporal
efetivo.
do
fator
dias
»
dias
41
4.3.2
- Balanceamento de neutrons
0 b a l a n c e a m e n t o de n e u t r o n s de u m r e a t o r £ u m q u a d r o importante
a ser observado
e discutido
por e s t a r diretamente
com p a r â m e t r o s
como o f a t o r de m u l t i p l i c a ç ã o ,
a distribuição
de potência.
a razão
relacionado
de r e g e n e r a ç ã o
A Tabela 4.3 apresenta inicialmente
e
o balan-
ceamento de n e u t r o n s e m todo o r e a t o r ; e m s e g u i d a , n e s t a ordem, o b a l a n ceamento de n e u t r e rs n o c a r o ç o , n o c o b e r t o r r a d i a l
e no coDertor axial
N o r e a t o r como u m t o d o , os d o i s s i s t e m a s em
e UOg, não a p r e s e n t a m d i f e r e n ç a s
a fuga de n e u t r o n s .
Para o Th
consideráveis
a fuga r a d i a l
mente menor ( q u a s e q u a t r o v e z e s )
estudo,
e x c e t o n o que
de n e u t r o n s i
se
Th
refere
consideravel-
d e v i d o a duas r a z õ e s b á s i c a s :
a
secção
de choque m i c r o s c ó p i c a de c a p t u r a do T h ê m a i o r que a do U - 2 3 8 e m
f a i x a de e n e r g i a , p r a t i c a m e n t e
pastilhas
metálicos
dois
(Tabela 2.2)
pois aquele
acha-
e n q u a n t o o U - 2 3 8 se e n c o n t r a n a forma
de UOg. 0 b a l a n c e a m e n t o
a consequência destes
toda
( A p ê n d i c e B ) , e e também m a i o r a f r a ç ã o d e
volume o c u p a d a p e l o T h n o c o b e r t o r r a d i a l
se n a forma de b l o c o o
.
fatos:
de n e u t r o n s n o c o b e r t o r r a d i a l
de
mostra
t a x a de c a p t u r a m a i o r de ü m c o b e r t o r r a
d i a l de T h e m r e l a ç ã o a u m de UOg, ou s e j a , menos n e u t r o n s e s c a p a n d o ra di a l m e n t e .
N o caroço do r e a t o r ,
s ã o m a i o r dos i s ó t o p o s f T s s e i s
a T a b e l a 4 . 3 r e v e l a uma t a x a de
fis¬
p a r a u m c o b e r t o r de Th. A l e m ' d a m a i o r
ta¬
x a de c a p t u r a d o T h , d i s c u t i d a a n t e r i o r m e n t e ,
i s t o também e r e s u l t a d o
comportamento d a s e c ç ã o de choque de f i s s ã o dos i s ó t o p o s T h - 2 3 2 e
e m função d a e n e r g i a do n e u t r o n m o s t r a d o n a F i g u r a 4 . 2 .
ção ao T h - 2 3 2 .
a p r e s e n t a m a i o r numero d e f i s s õ e s ,
do
U-238,
0 U - 2 3 8 , em rela¬
i s t o é,
contribue
com
F16 4 . 2 -
Secção
principais
de choque
isótopos
de
fissão
férteis.
dos
43
um número m a i o r de n e u t r o n s p a r a a m a n u t e n ç ã o da r e a ç ã o em
to pode s e r também c o n s t a t a d o p e l o b a l a n c e a m e n t o
tor
cadeia.
de n e u t r o n s
no
radial.
Tabela
4.3
-
Balanceamento
'
normalizado
1) NO REATOR
de
para
neutrons
1000
neutrons
Th
)
U0
2
Fissões
Em i s ó t o p o s
fTsseis
280
274
Em i s ó t o p o s
férteis
74
80
Em i s ó t o p o s
fTsseis
56
60
Em i s ó t o p o s
férteis
478
437
52
64
14
14
Radial
12
40
Axial
34
31
Capturas
Absorções
Na e s t r u t u r a
Em p r o d u t o s
de f i s s ã o
Fuga
Alfa
(físsil)
0,200
0,219
Eta
(físsil)
2,45
2,42
0,205
0,221
1,41
1,30
Epsilon
(fértil)
Razão de r e g e n e r a ç ã o
Is
cober-
44
Continuação
Tabela
4.3
2) NO CAROÇO
Th
U0
2
Fissões
E m isótopos fTsseis
263
254
E m isótopos férteis
64
64
E m isótopos fTsseis
52
53
E m isótopos férteis
184
188
Na estrutura
30
30
E m produtos d e fissão
13
13
E m isótopos fTsseis
8
11
E m isótopos férteis
3
10
E m isótopos fTsseis
1
4
Em isótopos férteis
199
151
Na estrutura
4
11
E m produtos de fissão
0
0
Capturas
Absorções
3) NO CCBERTCR RADIAL
Fissões
Capturas
Absorções
45
Continuação
da T a b e l a
4.3
4) NO COBERTOR AXIAL
Th
UOg
Fissões
Em i s ó t o p o s f í s s e i s
9
9
Em i s ó t o p o s f é r t e i s
7
6
Capturas
Em i s ó t o p o s
fTsseis
3
3
Em i s ó t o p o s
férteis
95
98
11
12
0
0
Absorções
Na e s t r u t u r a
Em produtos
Os
da Secção
to
seis
4.3.1,
dois
de f i s s ã o
parágrafos
Primeiro
anteriores
, o c o b e r t o r de Th e x i g e u m
m a i o r n o c a r o ç o do r e a t o r p o r q u e a t a x a
deve s e r n e c e s s a r i a m e n t e m a i o r ,
maior taxa
de f i s s ã o ,
do
uma m a i o r q u a n t i d a d e
a b s o r ç ã o de n e u t r o n s
bela
a fração
2.2
),,
resultados
enriquecimen-
de i s ó t o p o s
fTs_
como c o n s e q u ê n c i a
de m a t e r i a l
ou s e j a ,
fTssH
da
e quei-
m a i o r queda da rea_
sistema.
No c o b e r t o r r a d i a l ,
pois
de f i s s ã o
Segundo,
mada n o c a r o ç o d u r a n t e o c i c l o do r e a t o r ,
tividade
explicam dois
pela e s t r u t u r a
alem dos c o m e n t á r i o s
anteriores,
£ menor p a r a o c o b e r t o r de
de volume o c u p a d a p e l o m a t e r i a l
estrutural
£ menor
a
Th
(Ta¬
46
N o c o b e r t o r a x i a l o b a l a n c e a m e n t o de n e u t r o n s e pratica
mente o mesmo p a r a os d o i s t i p o s de c o b e r t o r e s . A c o n c e n t r a ç ã o de mate,
rial
fértil
e estrutural
fluxo
de neutrons
para
o outro.
não depende do c o b e r t o r r a d i a l
incidente
Os v a l o r e s
velam
naquela r e g i ã o pouco d i f e r e
encontrados
utilizado
de um
para os p a r â m e t r o s
e o
sistema
alfa e eta re-
que a e n e r g i a média do e s p e c t r o de n e u t r o n s £ um pouco maior pa-
ra o c o b e r t o r de Th, o que pode s e r c o m p r o v a d o p e l a Figura 4.3. A menor
t a x a de f i s s ã o
do Th r e s u l t a num menor v a l o r de e p s i l o n , enquanto
a maior taxa de captura produz uma maior razão de
4.3.3 - Produção
de
material
A principal
que
regeneração.
fTssil
caractenstica
p r o d u z i r uma q u a n t i d a d e de massa f T s s i l
de um r e a t o r r e g e n e r a d o r
é
que e x c e d a s e u próprio consumo.
A F i g u r a 4.4 mostra o e x c e s s o produzido e m função d o tempo para os d o i s
tipos
de cobertor r a d i a l .
Contudo o i s ó t o p o f T s s i l
U-233 produzidos
no
c o b e r t o r de Th não é o mesmo consumido no c a r o ç o do r e a t o r . A Figura 4.5
tem m e l h o r s i g n i f i c a d o
pois mostra a produção f T s s i l
de ambos os s i s t e m a s . A produção f T s s i l
maior,
produção
tor
U0
tos
do c o b e r t o r de Th £ obviamente
dada a m a i o r t a x a de c a p t u r a p e l o
Um r e s u l t a d o
fTssi1
interessante
da p r i m e i r a f i l e i r a
do cobertor radial
isótopo
fértil
(Secção 4.3.2
, e x t r a í d o da Figura 4.5, é
de e l e m e n t o s
),
a
c o m b u s t T v e i s do cober
de Th que £ e q u i v a l e n t e a p r o d u ç ã o de duas fil e i r a s de e l e m e n t o s de
2
. I s t o sugere i m r e a t o r GCFR menor, c o m uma ú n i c a l i n h a d e elemen de t ó r i o m e t á l i c o . Tal
situação
redundaria uma melhor
do t ó r i o sob o ponto de v i s t a n e u t r ô n i c o .
utilização
0 r e a t o r sugeri do £ estudado
i»SIiuii> r
lO*
.. I....
0
lQ>
'
lO«
t
1
lO*
I
-
lO'
lOP
lO'
l2
Fiçj. 4 - 3 a
II
_ Espectro
lO
médio
9
de
S
neutrons
7
no
f.
caropo
.
do
5
GCFR
4
3
protótipo
2
com
lO
cobertor
iearga
de
Th.
s
10*
10
10"
10"
K>
10°
eV
10*
10'
l
X3
O
•O
i0°
10"'
I
3
12
Fig. 4 - 3 b - E s p e c t r o
1
10
medio
de
neutrons
no caroço
GCFR
prototipo c o m
0
Letargia
um cobertor
de U0„
2 5 0
F I G - 4 .
4
-
M A S S A
R A D I A L
5 0 0
FÍSSIL
E M
A C U M U L A D A
F U N Ç Ã O
D O
7 5 0
N O
T E M P O .
C O B E R T O R
DIA»
50
na Secção
4.3.4
4.4
- Razão de „ a m y e r j j j o _ i n t e m a
A
e d i s t r i b u i ç j o , , de p o t i n c i a
A razão de conversão de cada zona do caroço £ a p r e s e n t a d a
na Tabela 4.6. Em ambos os sistemas as zonas mais
internas
apresentam
r a z õ e s de c o n v e r s ã o m a i o r e s em v i r t u d e de menores e n r i q u e c i m e n t o s , ou se_
j a , m a i o r t a x a de c a p t u r a p e l o s
isótopos f é r t e i s .
Pelo
mesmo m o t i v o
as
zonas dq c a r o ç o o p e r a n d o com u m c o b e r t o r de Th possuem r a z õ e s de r e g e n e r a ç ã o menores em r e l a ç ã o a q u e l a s c e r c a d a s p o r U0,,.
massa f í s s i l
menor n o
caroço
( Secção
uma
a d e n s i d a d e de p o t ê n c i a
obti_
N o c a r o ç o , os v a l o r e s mais a l t o s o b t i d o s
para
o c o b e r t o r de T h s ã o c o n s e q u ê n c i a das m a i o r e s t a x a s
por aquele t i p o de c o b e r t o r
prio cobertor radial
exige
4.3.1).,
N a mesma T a b e l a a p r e s e n t a - s e
da em cada zona do r e a t o r .
0 UOg
de f i s s ã o
requeridas
( Secção 4 . 3 . 2 ). 0 i n v e r s o a c o n t e c e n o pró¬
. Sob o p o n t o de v i s t a f í s i c o
o c o b e r t o r de UOg per,
mi te u m m e l h o r c o m p o r t a m e n t o do c a r o ç o do reator p o i s a d e n s i d a d e de po¬
tência
v a r i a mui t o pouco de zona p a r a z o n a .
Isto significa
uma queima de
c o m b u s t í v e l praticamente u n i f o r m e . N o c a s o do Th, a zona do c a r o ç o a d j a c e n t e ao cobertor radial possue uma densidade de p o t ê n c i a b a i x a em r e l a ção is o u t r a s t r ê s .
A explicação vem o u t r a v e z da Secção 4 . 3 . 2 : o
b e r t o r de Th f o r n e c e menos n e u t r o n s
p o r f i s s i o n a r menos que e s t e .
n a 4, e, p r o p o r c i o n a l m e n t e ,
co -
a zona 4 d o que o c o b e r t o r de
A s s i m , £ d i m i n u i da a t a x a de f i s s ã o
sua densi dade d e p o t ê n c i a .
da zo¬
51
T a b e l a 4 . 4 - Razão de c o n v e r s ã o e d e n s i d a d e
(ver
Razão de
Th
Zona
Figura
2.4
de p o t i n c i a em cada
zona
).
Densidade
Th
Conversão
uo
2
de p o t i n c i a W/cm3
Zona 1
0,750
0,779
257
237
Zona 2
0,613
0,639
250
236
Zona 3
0,514
0,540
233
227
Zona 4
0,400
0,439
209
217
14
19
2
7
23
22
18
17
13
13
8
8
Cob.Rad.l
-
Cob.Rad.2
-
Cob.Ax,, 1 ,
-
-
Cob.Ax. 2
-
Cob.Ax.
3
. -
-
-
Cob.Ax. 4
4.3.5
-
Produção
de
U-232
A formação de U-232 £ i n e r e n t e ao c i c l o do t ó r i o
t o p o £ formado a t r a v i s
(1)
(2)
Th-232(n,2n)
U-233 ( n , 2n)
0
de duas r e a ç õ e s
Th-231
e
»
25,6 h
. Este
is6
:
Pa-231(n,
Y
) Pa-232
e
1,32
-»
d
U-232
U-232
U-232 £ c o n t a m i n a n t e em v i r t u d e do seu d e c a i m e n t o .
A
ro
cadeia i n i c i a d a pelo
U-232
e
a
U-232
»• Th-228
74 a
Rn-220
mostrada
a
a
» Ra-224 — 2 — » Rn-220
1,91 a
3,64 d
Po-216 — 2 — * P b - 2 1 2
0,16 S
55 s
seguir:
JL
10,6 h
3,
-T1-208
Bi-212
Y
3,1 m
Bi-212
„Pb-208
(estável)
Po-212
0 , 3 4 yS
0 d e c a i m e n t o do B i - 2 1 2 e acompanhado de r a d i a ç õ e s
alta energia
( 0,4 - 2,1
MeV)
. Devido a v i d a l o n g a do
vi da de 74 a n o s ) , l o g o após r e t i r a d o do r e a t o r ,
l a t i vãmente pouca r a d i a ç ã o .
atividade
terá
crescido
Semanas mais tarde»
o sufuciente
para
de blindagem n o manuseio do m a t e r i a l
custos
do
U - 2 3 2
de r e p r o c e s s a m e n t o
porem
requerer
(
U - 2 3 2
o m a t e r i al
gama de
meia-
emitira
re
, o nível
cuidados
de
especiais
i r r a d i a d o , encarecendo assim
s fabricação.
e um p a r â m e t r o de i n t e r e s s e
Por e s t a
especial
razão
a
os
concentração
p a r a a economia do
sis-
tema .
Neste estudo
(1)
Os
Th-232
a primeira
(n,2n)
decaimentos
reação
Pa-231
(n, )
y
- 750
simplificada
para
:
U-232
s" i n t e r m e d i á r i o s
p o i s os tempos de meia v i d a são d e s p r e z í v e i s
irradiação
foi
não foram
considerados
em face do tempo
dias.
SÍ ]i íí
de
5 3
A
M E N T O
de
RA
4 . 6 .
DA
P O R
DE
M A I O R
4.4
-
C O N C E N T R A Ç Ã O
P R I M E I R A
N E S T A
E S T A R
F I L E I R A
F I L E I R A
DO
A
A D J A C E N T E
A O
C O B E R T O R
R A B I E
"
D E
E S T U D O ,
A P R O X I M A - S E
T H O G
C O M
P A R A
F I N S
D A
F I S S Ã O
P E L A
OR
M U I T O
D I F E R E N Ç A S
M E N T O
C A R O Ç O
br
F U N Ç Ã O
R E D I « 1
DE
do
U - 2 3 2
R E C E B E N D O
DO
Th
£
T E M P O
?.
M O S T R A D A
M A I O R
A S S I M
U M
P A R A
DO
NA
Q U E
F L U X O
UM
F I G U -
N A
D E
E L E _
S E G U N -
N E U T R O N S
3
F I L E I R A S
D E
DO
D E
Th-232
M A I O R
T A X A
E M
D E
A
O
NO
R A Z Ã O
AO
P O R
C A R O Ç O .
DE
E L E M E N T O S
P A R A
S E R Ã O
O
P A R T E
NO
D O S
DO
DE
C O B E R T O R
I S Ó T O P O S
M E S M O
R E A T O R
N E U T R O N S
U 0 ,
A S S I M ,
A U M E N T A N D O - S E
C O N V E R S Ã O
O
J U S T I F I C A D A S
F £ R T E I S .
U-238
P R O P O S T O
C O N S I D E R A D O S
DE
S E R
T E M
P A R A
C O B E R T O R
P O D E M
I S Ó T O P O S
R E L A Ç Ã O
711/27/
G A
B A L A N C E A M E N T O
O B T I D O
D E
F I S S Ã O
E N R I Q U E C I M E N T O
D I M I N U E - S E
DE
S I G N I F I C A N T E S
F I S S Ã O
D A
C O M P A R A Ç Ã O ,
Q U E
D A Q U E L E
M A I S
T A X A
T B F U
R E L A T Ó R I O S
N O T A - S E
A S
C O B E R T O R
EM
I N T E N S I D A D E .
R A D I A L
N E S T E
U--232
C O N C E N T R A Ç Ã O
R E C E N T E S
T O R
DE
O
E
A
A
A P E N A S
4.5
)
(Tabela
4.3
) .
M E N O R
E
C O M P O R T A -
T A X A
DE
R E S P O N S Á V E L
E X I G I N D O R N A I *
E N R I Q U E C I M E N T O
DE
D U A S .
( T A B E L A
F Í S S E I S ,
R A Z Ã O
C O B E R
P R O T O T I P O .
P E L O
R A D I A L
UM
CO CarOÇO
R E G E N E R A Ç Ã O
DO
R E A T O R .
EM
D I Z
R E S P E I T O
M E N O R
R A D I A L
P A R A
D E
R E G E N E R A Ç Ã O
O
A
R E L A Ç Ã O
T A X A
ThO,,
D E
•
N E U T R O N S ,
M E N O R .
A O
C O B E R T O R
C A P T U R A "
C O M O
D O S
TH
I S Ó T O P O S
C O N S E Q U Ê N C I A ,
P R O D U Z I N D O
D E
M E N O S
O
A
Ú N I C A
F É R T E I S
ThCT
M A T E R I A L
D I F E R E N Ç A
N O
P E R M I T E
F T s S I L
N O T Á V E L
C O B E R T O R
R A D I A L »
U M A
M A I O R
F U G A
-
R A Z Ã O
DE
100
Figura
200
4-5
300
400
- Concentração
fileira
-ção
de
do
de
500
U-232
elementos
tempo.
de
600
na
primeira
Th
em
fun-
700
dias
55
Tabela
4.5
Balanceamento
-
Th0
-
F iss õ e s
2
(
de n
utron s
para'
normalizado para
um
cobertor
1000 n e u t r o n s
Rea—o r
.
8
3
)
Caroço,
2
d e
6
Cob.,
4
Radial
E
m isótopos
Em
Isótopos
férteis
72
65
2
Em
isótopos
físseis
58
54
1
Em
isótopos
férteis
438
1 9 0
62
32
8
14
13
0
físseis
2
radial
9
1 4 9
Absorções
Nâ
estrutura
Ern p r o d u t o s
de
fissão
Mi
Al
Eta
Radial
3 7
Axial
36 '
f i
0,205
(físsil)
(físsil)
Epsilon
(fértil
Razão d e
2,44
)
regeneração
0,201
1,27
56
Tabela
4.6
Balanceamento
a 1
de
tíveis
Th
com
de
neutrons
para
uma
fil ei ra
de
"normali zado
Reator
para
o
coberto
elementos
1.000
radi_
combus-
neutrons "
Caroço
Cobertor
ftadial
Axial
Fissões
264
S
férteis
65
7
Em isótopos físseis
S2
Em isótopos
físseis
Em i s ó t o p o s
280
Capturas
Em isótopos férteis
437
IEE>
1 5
7
95
Absorções
N a estrutura
12
Em produtos de fissão
1 3
Fuga
Radial
Axial
40
Alfa
{fTssil)
0,200
Eta
(físsi!)
0,205
Epsilon
Razão de
(fértil)
regeneração
2,45
1,30
0
0
57
4.5 - C o b e r t o r r a d i a l
de Th com uma ú n i c a f i l e i r a
A
de
elej entos
A
N a Secção 4 . 3 . 3 u m r e s u l t a d o e a p r e s e n t a d o . A p r i m e i r a
fileira
de e l e m e n t o s
zir tanto material
férteis
físsil
de Th n o c o b e r t o r r a d i a l
q u a n t o duas
de U 0
2
e capaz de prod_u
n a forma de p a s t i l h a s
E s t a S e c ç ã o t r a t a da a v a l i a ç ã o de u m c o b e r t o r r a d i a l
dimensões>
i s t o £, com uma ú n i c a f i l e i r a
de n e u t r o n s
para tal
E m r e l a ç ã o ao UCA
nor taxa
parte
sentada
de f i s s ã o
dos i s o t o p o s
fîsseis
pelo material
is
e e x i g e m a i o r t a x a de f i s s ã o p o r
n o c a r o ç o do r e a t o r .
isto
se deve u n i c a m e n t e
No
estrutura
A mesma d i s c u s s ã o
s e n t i d o axial
dois
apre
resultados
m
»
como a x i a l m e n t e . N o
a menor f r a ç ã o
de volume
A s s i m s menos n e u t r o n s
e» c o n s e q u e n t e m e n t e ,
são
mais n e u t r o n s
ocupada
capturados
escapam
do
p o r q u e o e s p e c t r o de n e u t r o n s n o c a r o ç o e ma-
r á p i d o p a r a o c o b e r t o r de Th
trons
4.6,
a fuga de n e u t r o n s £ m a i o r t a n t o r a d i a l
radial
balanceamento
e s t e c o b e r t o r menor a p r e s e n t a me -
9
férteis
p e l a e s t r u t u r a n o c o b e r t o r de Th.
reator.
na Tabela
0
na Secção 4 . 3 . 2 £ v a l i d a para e x p l i c a r e s t e s
Alem d i s s o ,
sentido
de i s ó t o p o s
de Th de menores
de e l e m e n t o s .
caso a apresentado
„
, Quanto mais r á p i d o s
que a t i n g e m o c o b e r t o r a x i a l
menos
neutrons
forem os
neu¬
serão capturados
pa
lo U-238 o que pode s e r c o n s t a t a d o p e l o c o m p o r t a m e n t o da s e c ç ã o de c h o que m i c r o s c ó p i c a
de c a p t u r a d e s t e i s ó t o p o
( Apêndice
B),
E m r e l a ç ã o ao c o b e r t o r de Th mais e s p e s s o » um r e s u l t a »
do v a l e a pena s e r
comentado:
- produção f í s s i l
de e l e m e n t o s
do
cobertor radial
de T h , k g / a n o
com urna
fileira
87
58
Produção fTssll
tor
radial
Th,
kg/ano
da p r i m e i r a f i l e i r a
com 2 f i l e i r a s
do
de e l e m e n t o s
coberde
83
A p r o d u ç ã o não ê a mesma dado ao t i p o de m a t e r i a l
ternamente adjacente
aço, um material
a primeira f i l e i r a .
refletor
No primeiro
caso t r a t a - s e
de n e u t r o n s e no s e g u n d o , o m a t e r i a l
cante £ o próprio tÓrio metálico
caracteristicamente
ex¬
absorvedor
de
adja
de
n e u t r o n s . P o r t a n t o , p a r a o c o b e r t o r menor de Th m a i o r número de neu trons
i n c i d e na p r i m e i r a
( e única)
fileira
de e l e m e n t o s
uma m a i o r t a x a de c a p t u r a p o r p a r t e do T h - 2 3 2 .
propiciando
59
5.
CCNCIUSCES
O emprego de Th em l u g a r de U 0
GCFR p r o t ó t i p o m o s t r o u - s e
to de v i s t a n e u t r ô n i c o .
j o s o n o que se r e f e r e
g u i d a os v a l o r e s
(1)
no
caroço
como
pode
Th
£ o que
no caroço no
basicamente £ resultado
Th
n e u t r o n s do que o
C o m e n t a - s e em
exige maior
Th
U02
Th02
1253
1200
1229
iní-
e
kg
.U0
foi
2
Th em
2
d i s c u t i d a na Secção
d e v i d o a p r e s e n ç a do
e
rei ação ao de
apresenta um valor i n t e r m e d i á r i o
U0
enriquecimen
pois
Th-232
de volume m u i t o m a i o r .
m a i o r q u a n t i d a d e de m a t e r i a l
palavras
ço
do
, o c o b e r t o r de
que o
de
Th.
Al£m d i s s o ,
estrutural
Th0
2
U0 -
mais
( Apindice B
Th.
ta-
Quaji
2
) e
ocupando
o c o b e r t o r de T h 0 2
do que o de
r e f l e t e mais
maior
captura
menos do que o Th p o i s o u l t i m o e n c o n t r a - s e na forma m e t á l i c a
uma f r a ç ã o
se-
abaixo:
da menor t a x a de f i s s ã o
xa de c a p t u r a p o r p a r t e do c o b e r t o r de
este
vanta-
parâmetros.
ser verificado
A diferença entre o
t o ao T h 0 2
sob o p o n -
Enriquecimento
c i o do c i c l o de e q u i l í b r i o ,
e
do
sobremaneira
fértil.
p a r a os p r i n c i p a i s
Massa f í s s i l
4.3.2
favorável
mostrou-se
a p r o d u ç ã o de m a t e r i a l
0 c o b e r t o r de
to
no c o b e r t o r r a d i a l
uma a l t e r n a t i v a b a s t a n t e
0 tório metálico
obtidos
2
o u , em
n e u t r o n s de v o l t a ao
possua
outras
caro¬
6 0
(2 ) P r o d u ç ã o
de
material
Neste aspecto
U0
2
ou
ao
de
ThQ
físsi V e taxa de
regeneração .
o c o b e r t o r de Th».a b a s t a n t e
ou
T h 0 ) são as c a u s a s
deste
2
( BS%
Produção
Taxa
fTssil
rio
, kg/ano
de r e g e n e r a ç ã o
calculando-se o
Í definido
z i r um
aqui
o
tempo
massa
fTssil
como
excesso de
tempo de
U09
1,42
1,30
) e ( 2
igual
para
o
reator
) podem s e r com-
mento
cobertor
Th.
11,1
2
12
2
Embora podendo também s e r
outros
Th02 apresenta
dois t i p o s
)
8 ,6
Th0
o c o b e r t o r de
comporta
tp ( anos
Th
prodjü
necessita
revelam o
Cobertor
uo
Este
regenerador
a q u a n t i d a d e q u e o mesmo
Os números o b t i d o s
de
1,27
fTssil, tp.
d u p l i c a ç ã o d e massa
necessário
80
83
equilíbrio.
do
Th0o
112
n o i n í c i o do c i c l o de
superior
,
cobertor
Os resultados apresentados em ( 1
binados
p a r a o Th
resultado.
Th
radial
de
. A m a i o r t a x a de c a p t u r a de n e u t r o n s p e l o primei_
2
ro a l i a d a a m a i o r f r a ç ã o de volume ocupada no c o b e r t o r
50% p a r a UOg
s u p e r i o r ao
como
considerado
um comportamento
o s números*
indicam,
uma boa
neutrônico
,8
alternativa
inferior
aos
Lm meio d e m e l h o r a r i s t o sfe
61
ria
p e l o emprego de uma t e r c e i r a
dial
como a General
tes
¡211.
A
fileira
de e l e m e n t o s
no
cobertor
Atomic tem s u g e r i d o em s e u s r e l a t ó r i o s
mais
fuga de n e u t r o n s s e r i a diminui da e a t a x a de
e produção f í s s i l
siginificativo
aumentadas.
do r e a t o r
i m p l i c a n d o em m a i o r e s
(3)
e,
Uma d e s v a n t a g e m ,
porém,
consequentemente,
do
investimentos
Distribuição
de
de
ra-
recen-
regeneração
seria o
aumento
v a s o de p r e s s ã o
,
capital,
potência
Abaixo são r e p e t i dos os v a l o r e s
da zona do c a r o ç o s e g u n d o o c o b e r t o r r a d i a l
encontrados
para
ca¬
utilizado
3
D e n s i d a d e de P o t e n c i a ,
Th
U0?
Th0
Zona 1
257
237
256
Zona 2
250
236
257
Zona 3
233
227
244
Zona 4
209
217
226
E m ambos os s i s t e m a s que usam Th-232 rio c o b e r t o r
a densidade
or
a
plano
de
t o r em
z o n a s mais
isto
estudo.
nos n e u t r o n s
U-238.
de p o t ê n c i a
na zona 4 m o s t r a - s e
internas,
prejudicando
p a r a a c u r v a de d i s t r i b u i ç ã o
teriormente
w/cm
ê causado pelas
A
zona 4
refletidos
, adjacente
inferi¬
assim o desejado
perfil
Conforme
refletivas
discutido
de
ao c o b e r t o r r a d i a l ,
cada
recebe
n e s t e " ú l t i m o quando o Th-232 s u b s t i t u e
Uma s u g e s t ã o s e r i a a de v a r i a r o e n r i q u e c i m e n t o nas z o n a s
c a r o ç o de modo a se t e r a d i s t r i b u i ç ã o
radial,
significativamente
de p o t ê n c i a .
propriedades
2
de p o t ê n c i a
desejada
.Tal
an
cobejr
me¬
o
do
estu-
62
d o , porem
, não faz
parte
dos
objetivos
deste
t r a b a l ho.
O u t r a vantagem do Th em r e l a ç ã o ao U 0 ( T h 0 ) ,
2
c i a da m a i o r t a x a de c a p t u r a ,
aquele
cobertor
consequên-
2
e a menor fuga de n e u t r o n s
do
reator
que
proporciona.
Fuga r a d i a l
(para
de n e u t r o n s
1000 n e u t r o n s
Th
U02
Th02
12
40
37
produzi¬
dos)
Assim, o c o b e r t o r r a d i a l
de Th faz d i m i n u i r as
des de b l i n d a g e m e x t e r n a do r e a t o r p o i s o p r ó p r i o
necessidjs
cobertor atua
como
uma f o r t e b l i n d a g e m de n e u t r o n s .
0 cobertor radial
Th e s t u d a d o na Secção 4.5
bus t i v e !
firtil.
com a p e n a s uma f i l e i r a
possibilitaria
A segunda f i l e i r a ,
de e l e m e n t o s
uma m e l h o r u t i l i z a ç ã o
quando p r e s e n t e ,
sofre
rável
obtidos
Os parâmetros
integrais
-
conside-
a p r e s e n t a m v a l o r e s b a s t a n t e p r ó x i m o s aos
p a r a o c o b e r t o r de U 0 2 .
U02
fileira)
1,29
Fuga r a d i a l
40
44
83
87
físsil
do
cobertor
kg/ano
O u t r a vantagem em se u t i l i z a r
minuição sensível
ser
1
1,30
radial,
a
Th(
Taxa de r e g e n e r a ç ã o
Produção
pressão
do com
uma f o r t e
b l i n d a g e m da p r i m e i r a que não l h e p e r m i t e uma p r o d u ç ã o f í s s i l
de
a p e n a s uma fi 1 ei ra ê a d i -
do tamanho do r e a t o r e, p o r c o n s e g u i n t e
utilizado.
, do v a s o
de
63
APÊNDICE
A
- H i p ó t e s e s p a r a o c a l c u l o do r e a t o r GCFR de
1 . Geometria :
RZ
- Dimensões na
Figura
A.l
-4
2.
Densidades
Tabela
referência.
atomicas,
A.l
10
Densidade
átomos/barn.cm
atômica
dos
isótopos
pesados
Isótopo
Zona 1
Zona 2
Zona 3
Zona 4
Cobertor
radial
Cobertor
axial
U-235
0,0647
0,0679
0,0659
0,0719
0,2678
0,1089
U-238
38,38
38,30
35,50
36,40
110,43
48,51
Pu-239
5,36
5,959
6,581
7,748
0,6698
0,7330
Pu-240
2,276
2,591
2,934
3,430
0,0065
0,0120
Pu-241
0,3609
0,4201
0,4858
0,5830
Pu-242
0,1707
0,1958
0,2232
0,2618
2,789
2,781
2,70
2,425
0,210
0,148
Produ; os
fissão
64
APÉNDICE
Tabela
\
(contO
A.2 -
Isótopo
Densidade
atômica
Zonas do c a r o ç o
+ cobertor
dos
átomos
Cobertor
axial
e
axial
583,0
62,25
90,57
Cr
15,92
22,80
N,
12
17,89
Mo
1,84
2,628
Ox
99,89
223,00
He
5,638
2,925
,49
estrutura
Cobertor
radial
Fe
3 c Potencia
da
-
-
termica
2680 MW
4.
Estrutura
dos
Grupo
grupos
de
energia
Limite
superior
, eV
1
1,00
x
IO
7
2
1,40
x
IO
6
3
4,00
x
IO
5
4
2,00
x
IO
5
5
4,65
x
IO
4
6
1,00
x
IO
4
7
1,00
x
IO
3
radial
APÊNDICE
5o
A
Definição
( cont).
do
reticulado
Numero t o t a l
( mesh )
de p o n t o s
:
42
x
32
Al t u r a :
137,6
4 x 2,50
127,6
13 x 4 , 6 1 5 4
67,6
14 x 4 , 8 2 8 6
0,0
Raio:
0,0
12 x 6 , 1 0 8 3
73,3
4 x
5,2250
94,2
4 x 4,2750
111,3
5 x 4,760
135,1
12 x 5,0
195,1
4 x 2,50
205,1
INSTITUTO Of
1 3
7 , 6
Refletor
127,6
z (cm)
Cobertor
axial
67 6
Cobertor
r a d i al
Zona 1
Zona 2
73,3
Zona 3
94,2
Zona 4
111 ,3
135,1
195,1
205,1
r(cm)
FIG. A.I - Dimensões de u m q u a r t o do r e a t o r
e r
(Ti
c i l i n d r i z a d o e q u i v a l e n t e ao GCFR d e
referência
67
APÊNDICE B - S e c ç õ e s de choque e f e t i v a s de c a p t u r a e f i s s ã o dos
pos U - 2 3 8 e T h - 2 3 2
Grupo
em
30
grupos
de
isõto
energia
L i m i t e superior
de
e n e r g i a eV
Th-232
U-238
Th-232
U-232
x IO
7
0,012
0,007
0,286
0,877
6,07 x 10
7
0,021
0,011
0,142
0,547
3,68 x IO
6
0,040
0,027
0,124
0,547
2,23 x IO
6
0,079
0,063
0,092
0,427
1,35 x I O
6
5
0,142
0,121
0,002
0,027
6
8,21
x IO
5
0,177
0,126
0,0
0,0013
7
4,99
x IO
5
0,179
0,115
0,0
0,0002
.8
3,88 x I O
5
0,178
0,118
0,0
0,0001
9
3,02 x I O
5
0,184
0,135
0,0
0,0001
10
1,83
x IO
5
0,218
0,170
0,0
0,0
11
1,11
x IO
5
0,290
0,216
0,0
0,0
12
6,74 x IO
4
0,381
0,336
0,0
0,0
13
4,09 x IO
4
0,453
0,435
0,0
0,0
2,55 x IO
4
0,537
0,497
0,0
0,0
4
1
2
3
1 4
15
1,00
1,99
x IO
0,602
0,571
0,0
0,0
0,705
0,649
0,0
0,0
16
1 ,50 x I O
4
17
9,12 x I O
3
0,863
0,763
0,0
0,0
18
5,53 x I O
3
1,07
0,849
0,0
0,0
19
3,35 x I O
3
1,39
1,09
0,0
0,0
20
2,84 x IO
3
1 ,53
0,936
0,0
0,0
21
2,40 x I O
3
1,60
1,03
0,0
0,0
22
2,03 x I O
3
2,15
1,01
0,0
0,0
23
1,23
x IO
3
2,16
1,31
0,0
0,0
24
7,49 x I O
2
4,35
1,31
0,0
0,0
25
4,54 x IO
2
7,10
1,20
0,0
0,0
26
2,75 x IO
2
9,71
1,46
0,0
0,0
27
2,30 x IO
2
27,4
2,86
0,0
0,0
28
6,14 x IO
1
29,8
3,44
0,0
0,0
29
1,37
x IO
1
0,410
1 ,03
0,0
0,0
30
6,83 x IO"
0,0003
29,2
0,0
0,0
1
68
APÊNDICE
C
1
•* B a l a n c e a m e n t o de n e u t r o n s do GCFR p r o t ó t i p o cem c o b e r tor
de Th - em 12 e em
(1) N o r e a t o r
4 g r u p o s de
12 g r u p o s
energia
4
grupos
Fissões
Em i s ó t o p o s f T s s e i s
278
280
Em isótopos f é r t e i s
74
74
Em i s ó t o p o s f T s s e i s
55
56
Em isótopos f é r t e i s
478
Capturas
4
7
8
Absorções
Na e s t r u t u r a
52
52
E m p r o d u t o s de f i s s ã o
13
14
Radial
12
12
Axial
37
34
Alfa
(fTssil)
0,202
0,200
Eta
(fTssil)
2,44
2,45
0,206
0,205
Epsilon
(fértil)
Taxa de r e g e n e r a ç ã o
(2)
1,42
1 , 4 1
No caroço
Fissões
Em i s ó t o p o s f T s s e i s
261
263
APÊNDICE
C
(conto)
Em i s ó t o p o s
férteis
Captura
Em i s ó t o p o s
físseis
Em isótopos
férteis
Na
estrutura
E m p r o d u t o s de
(3) N o e n v o l t ó r i o
fissão
radial
F; ssoes
L
Em isótopos
físseis
Em isótopos
férteis
Captura
Em isótopos
físseis
Em isótopos
férteis
Absorções
Na
estrutura
Em produtos
de
fissão
70
APÊNDICE
C
( cont.
)
12 g r u p o s
(4)
No envoltório
4
grupos
axial
Fissões
Em i s ó t o p o s f T s s e i s
9
9
Em i s ó t o p o s f é r t e i s
6
7
Em i s ó t o p o s f T s s e i s
2
3
Em i s ó t o p o s f é r t e i s
94
95
Na e s t r u t u r a
11
11
Em p r o d u t o s de f i s s ã o
2
1
Capturas
Absorções
71
APÊNDICE
1
D
-
Programa
COLLAPSE
T e n d o - s e u m c o n j u n t o de s e c ç õ e s de choque p r e p a r a d o
ra o p r o g r a m a QTATION
( v e r Secção
'105 da R e f . / 1 0 / ) ,
o p r o g r a m a C0L_
LAPSE p r o d u z um novo c o n j u n t o
com u m n ú m e r o menor de g r u p o s de
Usa-se o e s p e c t r o
de cada zona p a r a se e f e t u a r
fundamental
p&
a
energia.
condensa¬
ção.
D.l
- Algoritmo
utilizado
0 e s p e c t r o fundamental
, j>
(onde
g
£ um g r u p o de ener
y
g i a dos
NG
grupos o r i g i n a i s
), 5 o b t i d o a t r a v é s
NG
X""
Z ,
9
D Bi
g
V
- i
<k + v
• • renrg
g
x
1
de
v.
v
j
fj
v
o
NG
•
2
X
J * g *j
=
ô
>
j > g
onde,
NG
número de g r u p o s de e n e r g i a
de s e c ç õ e s
2
D B d>
g
g
de
do c o n j u n t o
original
choque;
número de n e u t r o n s
do grupo
g
que escapam
do
9
meio p o r u n i d a d e de volume p o r u n i d a d e de t e m p o ;
E
rem*g
numéro de n e u t r o n s r e m o v i d o s do grupo
dade de voltjme p o r u n i d a d e de t e m p o ;
g p o r uni_
72
APÊNDICE
D
(CONT)
NG
v
Xg
E
j fj
A
"
*j
número
A
zidos
de n e u t r o n s
de f i s s ã o
no grupo
, resultantes
fissões
g
em t o d o s os g r u p o s
produ_
de
, p o r uij_
dade de volume p o r u n i d a d e de tempo-,
NG
E.
J
*..
número de n e u t r o n s e s p a l h a d o s
> A
grupo g
p o r u n i d a d e de volume
unidade
de
Uma e s t i m a t i v a i n i c i a l
r e a l i z a um cálculo adimensional
de B
para o
por
tempo.
£ n e c e s s á r i a e o programa
por i t e r a ç õ e s
sucessivas
obtendo o va
de choque s ã o e n t ã o c a l c u l a d a s
na nova es -
2
l o r de
B
para a c r i t i c a l i d a d e
As secções
trutura
de g r u p o s
do meio.
de e n e r g i a p e l a s
g2
X
onde,
x = f,a,(n,2n)
;
equações:
[ g2
°xi»j
1
(D.2
73
A P Ê N D I C E
com
D
k2 > kl
(COnt) .
> g2 ;
1-1
l
° tn = Z
(D.4 )
). <|>.
"trlVí
j=gi
0 cálculo da secção de choque de transporte atravis fe
(D.4 ) mantém constante a componente d e fuga.
D . 2 - Cartões d e entrada
Cartão
1 ( 2413) - MG(L0N(K), K =
MG
1,MG)
número de novos g r u p o s ;
LON(K) limite inferior de energia dos novos grupos em função dos antigos.
C a r t ã o 2 (613) - M l ,
Ml
NSET, KFLUX KPRINT, UMAX
número do conjunto de secções de choque
(para efeito de saída de d a d o s ) ;
NSET ordem em que o conjunto de secções de cho que original
aparece n o arquivo
8 ;
KFLUX opção para se dar o espectro por cartões .
Exercida se KFLUX > 0 e o cartão 4 £ neces
sano;
74
APÊNDICE
D (cont).
KPRINT
opção a l i s t a g e m dos novos c o n j u n t o s
s e c ç õ e s de c h o q u e .
nMAX
E x e r c i d a se KPRINT >0.
numero máximo de i t e r a ç õ e s
lo d o
para o calcu¬
espectro.
C a r t ã o 3 (2413) - KNUCL,(IDEN(I),
KNUCL
1 = 1, KNUCL)
número de novos . i s ó t o p o s
cujas
choque devem s e r a c r e s c e n t a d a s
to original
(unidade
IDEN(I) número c ó d i g o do novo
Cartão 4 (6E12.5)
PHI(16)
de
lógica
secções
ao
de
conjun¬
10).
isótopo.
- ( P H I ( I G ) , IG=1,N6 )
f l u x o de n e u t r o n s
no grupo
IG.
0 c a r t ã o 4 £ d e s n e c e s s á r i o se KFLUX <_ 0. Os c a r toes
5 e 6 são d e s n e c e s s á r i o s
Cartão 5 (6(13.E9.5))
N6(K)
- (N6(K),C0N6(K),K = 1,6
número
conjunto
C0N6(K)
se KFLUX > 0.
)
c ó d i g o do i s ó t o p o p r e s e n t e
no
original;
c o n c e n t r a ç ã o do i s ó t o p o N6(K) no
(átomos/barn.cm);
meio
75
APÊNDICE
D
(cont)
Cartão 6 (2E12.4)
B2
- B2.EPS
E s t i m a t i v a do " b u c k l i n g " p a r a o i n í c i o
do
calculo.
EPS
critério
I
k
( n )
de c o n v e r g ê n c i a p a r a o a u t o v a l o r
- 1.0
I
k.
< EPS
onde,
k
A
autovalor
obtido
na
iteração
n.
U m novo c o n j u n t o de s e c ç õ e s de choque pode s e r p r o d u z i d o em
s e g u i d a a t r a v é s de u m novo c a r t ã o 2. U m c a r t ã o em b r a n c o e n c e r r a o " j o b " .
D.3 - U n i d a d e s
lógicas
U n i d a d e l ó g i c a 8 - A r q u i v o dos c o n j u n t o s
que
de s e c ç õ e s
de cho_
originais.
Unidade l ó g i c a 9 - A r q u i v o p r o d u z i d o p e l o p r o g r a m a C01LAPSE.
Unidade l ó g i c a
10- A r q u i v o onde se e n c o n t r a m as s e c ç õ e s
choque a serem a c r e s c e n t a d a s
8.
ao
de
arquivo
76
APÊNDICE
D
(cont.)
0 c a r t ã o 3 deve s e r d e i x a d o em b r a n c o quando não hou ver necessidade
na u n i d a d e 8.
de
10
rincia
d o uso das
constantes
nucleares
de i s ó t o p o s
ausentes
Quando u s a d o , p o r e m , o f o r m a t o das c o n s t a n t e s
na u n i d a
deve o b e d e c e r ao p a d r ã o e s p e c i f i c a d o
na s e c ç ã o
/10/.
Do4 - L i s t a g e m
INSTITUTO DE • ¿
105 da r e f e
-
c
********ZERU D I M E N S I O N A L
COLLAPSING
W R I T T E N 8Y
W J OGSTERKAMP
M O D I F I E D BY
A J FAYA
C
C
c
FOR
CITATION
*******
D I M E N S I O N I.O'I 50) » C H I ( 30) , C H J < 30 ) » E T ( 3 0 ) * E N ( 3 0 ) »RJ ( 3 0 ) ,OL ( 30)
1,GE( 3 0 ) ,NT ( 3 0 » 5) , I u I S t 5 0 , 6 » , A I 5 0 ,60 J . SA( 50 , 30 ) , S F ( 50,30>)
ItSTRC50,301 ,SNU( 5 0 , 3 0 ) , S X { 5 0 , 3 0 ) , S M T ( 5 0 , 3 0 » 3 0 ) , N O ( 6 ) , C 0 N 6 < 6 )
i , L O N ( 3 0 ) , K 0 N ( 3 Q ) , C O N (50) , P H I ( 30 ) , P H J ( 3 0 ) , 0( 3 0 ) t SRE1 30*t«S*t1O*
1»SA1(30),SF1(30),STR1{30)»SNU1 ( 3 0 ) , SX1(30),SMT1(30,30)»PHI1<30)
1,01(30)
DIMENSION
IDEN(IQ)
INTEGER
TIN,TOT
NIN= 3
NOT = 6
TIN = 8
T0T = 9
R E A 9 I N I N » 1 1 ) M G , ( L O N ( K ) » K = 1,MG )
NEtf=10
W R I T E ( N O T »5 99)
599
FORMATl/30X,»*****ZfcRG
DIMENSIONAL
COLLAPSING FOR
CITA?ftM******,
1//)
WRITE(o, 5 5 3MG,(LON(K),K=i,MG)
F O R M A T ( 5 X , ' N U M B E R O F N E W GROUPS«,I4,//,5X»»LQwER ENERGY 80UN0AR i ES
1 ',20I3)
15
REA0(NIN»11)M1»NSET»KFLUX» KPRINT»ITMAX
IF(Ml.EQ.O)
G O T O 300
R t A O (NI N» 11) KNOCL » (I D E N ( I ) , I = 1 , K N U C L )
11 F O R M A T ( 2 4 1 3 )
IF(1THAX.Ew.O)ITMAX=50
IT=0
R E W I N D TIN
D O 1 0 5 N S = 1 » hiSET
R E A D IT I N ) I I O ( K ) , K = 1 , l b )
READ{TI N.) NT» N N , N G , ND» NO»IMZ
READ I T I N ) 1 C H I ( 1 G ) »IG = 1» N G ) »(E T( I G ) » I G = 1 » N G ) , ( E N ( I G ) » I G = 1 » NG)
1 » ( R U ( I G ) ,i G = 1 » N G ) » 1 D L ( K ) ,K=1»10)» < G E ( K ) , K = 1 » 1 0 )
D O 10 N = l , N N
R tAD(TIN)
1 N I ( N , K ) , K = 1 , 5 ) ,(I 0 1 S (N, Mi » M = 1 » 6 ) , { A t N » H ) » M - 1 » 6 0 1
10 R E A D IT i N ) 1 S A ( N , I G ) , S F < N , I G ) , S T R ( N , IG ) , S N 0 ( N , IG) «S X ( N , IG) , I G= 1, HG )
1 » ( ( S M T ( N , IG » K G ) , K G = 1 , N G ) , I G = 1 » N G )
105
R E A D (TIN)
JG=1
DO 5 IG=1,NG
IF(IG.GT.LON<JG) ) JG=JG+1
5 K0N1IG)=JG
I F t K N U C L . E Q . O ) G Q TO 1515
W R I T £ ( N O T , b o 3d)
8 3 8 8 F O R M A T ( / » * * * * * O P T I O N FOR A D D I T I O N A L NOCLIOES EXERCISED'/)
NNl-NN+1
NN2-NN+KN0CL
D O 32 N - N N 1 , N N 2
R E W I N D NEW
READ(NEW)
READ(NEW)
READ(NEW)
55
8 32 0 R E A D - ( N E w , £ N D = 5 1 0 , E R R = 5 1 0 ) ( N I ( N , K ) , K = l , 5 ) , ( l D I S t N , M ) , M = l , 6 ) ,
1
tA(N,M),M=l,60)
R E A D (NEW ) ( SAIN» I-G) ,SF IN, I G ) S T R i N t I G ) , S N U ( N , I G ) , S X ( N , 1 G ) , I G = 1 , N G )
1,((SMT(N,IG,KG),KG=1,NG),IG=l,NG)
IF(NI(N,1)»N E » I D E N ( N - N N ) ) G O T O 8820
32 C O N T I N U E
NN=NN2
W R I T E ( N O T , 3 5 54)
5 5 5 4 F O R M A T (/» A D D I T I O N A L N U C L I D E S
FROM F I L E - N E W - / J
DO 5 55 5 N = N N 1 , N N 2
W R I 1 r;(N0T,55 5 o ) ( ID I S ( N , M ) , M = 1 , 6 )
5556 F O R M A T ( i H
, 10X,6A4)
5555
CONTINUE
1515
CONTINUE
IF(KFLUX.EO.O)G0
TO 727
WRITE(NOT,1325)
W R I T E (NO T » 1 4 4 4 ) M L
WR1TE (b,85)
85 F O R M A T ( / / , 5 X , «
NUCLIDES
IN T H I S
SET'/)
DO a 7 I N = 1 t N N
8 7 WRHE(o,8fa)( IDIS(IN»M),M«1,6)
86 FORM A T( IH , 1 0 X , b A 4 )
1D25 F O R M A T {'//• * * * * F L U X W I L L BE R E A D F R O M C A R D S ' / • G R O U P
FL
1UX» )
R E A D ( N I N , 8 1 ) ( P H I ( 1 G ) , I G = l,NG)
81
FORMAT(6F12.5)
W R I T f c i N U T , li>33) ( ( I G , P H i U G ) ) , I G = 1 , N G J
1533 F O R M A T ( »
«, I 5 , F 1 5 . 5 )
G U TO 747
727 D O 23 N = 1 , N N
23 C O N ( N ) = 0 .
WRITE!NOT,1444)Ml
2 0
READ(NIN,215)(No(K),C0N6(K),K=l,6)
2 1 5 .FORMAT ( 6 ( I 3 , F9 • 5 ) )
DO 3 0 K = l,6
IF(No(K).EQ.O)
G O T O 40
D O 30 N = l t N N
I F ( N 6 ( K ) . E w * N I (N,1)) C O N ( N J = C 0 N 6 ( K)
30 C O N T I N U E
GOTO 2 0
40 R E A D ( N I N , 4 1 )
B2,EPS
41 F O R M A T ( 6 t 1 2 • 4 )
IF(82.E0.0.)o2-0.001
IHEPS.Ew.O.ltPS=0.01
Xl=l.+2.*EPS
X2*1.-2.*EPS
WRITE
(6,56)
56 F O R M A T ( / / , 5 X , *
NUCLIOE^,17X,^CGNCENTRATION^/)
DO 5 8 I N = 1 , N N
58
WRITE(6,57)(IOISiIN,M),M=i,6),CON(INi
37 F O R M A T ( I H , 5 X , 6 A 4 , E 1 2 . 5>
100 X £ F F = u
DELTA1=D£LTA2
1T=IT+1
WRITE(6f133)IT
13 3 F O R M A T ( / / , *
ITERATION N O .
»,I3,/,' GROUP
FLUX
S
iSOURCE
REMOVAL
LEAKAGE
KEFF
BUCKLING
2 •/)
f
1
D O 1 1 0 I.G=1,NG
SRIIG)=CHI(IG)
DO 14 0 I G = I , M G
SF1S=0
SREM=0
ST = O
D O 130 N = 1 , N N
SFIS=SFIS+CDN(N)*SF(N,IG) *SNU(N,IG)
S R f c M = S R E M + C O N ( N ) * S A ( N , I G)
SMT(N,IG,IG)=0.
D O 120 K G = I G , N G
120 S R E M = S R E M + C O N 1 N ) * S M T ( N , I G , K G )
130
ST=ST+CtiNINJ*STR(N,IG)
PHI(IG)=SR(IG)/(SREM+B2/(3.*ST))
IFIPHI(IG).LT,0)PHlUG)=0.
SR E ( I G ) = S R E M * P H I ( I G )
D( I G ) = P H l l I G ) * B 2 / ( 3 « * S T )
XEFF=XEFF+SFIS#PHI(IG)
W R I T E ( 6 i 1 3 1 ) I G , P H I ( I G ) , S R ( I G ) , S R E ( I G ) , D ( I G ) » XEFF » B2
131 F O R M A T ( I 6 , O F 1 3 . 5 )
DO 140 K G = 1 , N G
DO 140 3i = 1 , N 'J
140 S R ( K G ) = S R ( K G ) + C O N ( N ) * S M T { N , I G , K G ) * P H I ( I G )
DlFF=AtiS(l.-XtFF)
IF(( I T . G T . 2 0 ) . A N D . ( X E F F . G T . X I ) ) X E F F = Xl
IF(( I T . G T . 2 0 ) . A N D . ( X E F F . L T . X 2 ) ) X E F F = X2
! F ( b 2 . G T . O . ) B2 = cJ2*XEFF
IF(B2.LT.O.)
B2=62/XEFF
IF(ABS(32).LT.0.0001)B2=-B2
IF( I T . G t . I T M A X ) G O T O 7 4 6
I F(D IF F . G T . 0 . 0 1 ) G G T O 1 0 0
GO TO 7 4 7
746 W R I T E ( 6 » 748) I T
7 4 B F O R M A T ! / / , * * * * * * N O CONVERGENCE AFTER
*,14,* I T E R A T I O N S * , /
1CR0SS S E C T I O N S WILL 6E C O L L A P S E D A C C O R D I N G L A S T
SPECTRUM*)
74 7 W R I T E < T U T ) ( 1 D ( K ) ,K = 1,18)
WRITE(TOT)NT,NN,MG,ND,NU,NZ
DO 150 JG=.1,MG
150 C H J ( J G ) = 0 .
DO lt>0 I G = 1 , N G
•JG=KON(IG)
loO CHJ ( J G ) =CHJ( J G ) + C H H I G )
wRI T E t T O T ) (CHJ(JG),JG = i » M G ) , ( E T ( J G ) , J G = 1 , M G ) » ( E N ( J G ) , J G - 1 » M G )
1, ( R U U G ) , J G = i ,MG ) » ( O L ( K ) ,K=1 ,10) , ( G E ( K ) » K = 1 , 1 0 )
DG220 N=1,NN
D O 170 J G = 1 , M G
SA1(JG)=0
S F1 ( J G ) = 0
SIR 1 ( J G ) = 0
SNU1(JG) . = 0
SX1(JG)=0
PHI1(JG)=0
Dl (JG)=0
D O 170 L G - 1 , M G
170 S M T I i J G , L G ) = 0
00 2 0 0
IG=1,NG
JG=KON(IG)
SA1(JG)=SA1(JG)+SA(N,IG)*PHI(IG)
110
f
*
*
*
*
»
S F K J G ) = S F K J G ) + S F ( N , I G ) * P H I (IG)
IF(KFLOX.EQ.O)STR1(JG) = S T R K J G ) + S T R ( N , I G ) * 0 ( I G )
IF(KFLUX.GT.O)STRKJG)=STR1(JG)+STR(N,IG)
*PHI(IG)
SNU1(JG)=SNU1(JG)+SNU(N,IG)*SF(N,IG)*PHI(IG)
SXKJG) = SX1(JG)+SX(N»IG)#PHI(IG)
PHI K J G ) = P H I K J G J + P H K IG)
IF('KFLUX.hg.O)
101 I J G ) = 0 1 ( J G ) + 0 ( IG)
0 0 2 00 KG=1,NG
LG=KON(KG)
2 00 S M T 1 ( J G , L G ) = SM T l ( J G , L G ) + S M T ( N , I G , K G ) * P H I ( I G )
00 2 1 0 J G = i , M G
S A K J G ) = S A K J G ) / P H I 1 (JG)
SFKJG)=SF1( JGl/PHIKJG)
IF(KFLOX.EQ.O)STRKJG)=STR1(JG)/Oi(JG)
1 F ( KF L JX . G T . 0 ) S TK 1 ( JG ) = S TR1 ( JG ) / PH I 1( JG )
I F ( S F K J G ) .NE.O.)
1SNUKJG)=SNU1(JG)/(SF1(JG)*PHI1(JG) )
SX1(JG)=SX11Jb)/PH11(JG)
00 2 1 0 L G = 1 » H G
210
SMT1(JG»LG)=SHT1(JG,LG)/PHIi(JG)
WRITE(TOT)(NI(N,K),K=1,5),(IDIS(N,K),K=1,6),(A(N,K),K=l,60)
W K I T E i T O T ) ( S A K J G ) , S F K J G ) ,STRl (JG) , S N U 1 ( J G ) , S X K J G ) , J G = 1 , M G )
It ( ( S M T1{J G » L G)» L G = 1 » M G ) , J G = 1 M G )
I F ( K P R l N T . E y . G ) G U TO 2 2 0
W R I T E ( N O T , 1 2 3 0 ) N I ( N , l ) , ( I D I S ( N , M ) , M = 1 6)
1444 F O R M A T ( / / / / , 3UX,« C R O S S S E C T I O N SET N O
«,I3)
1230 F O R M A T ! / / , 5 X , ' N U C L I D E N O » , 1 4 , 5 X , 6 A 4 )
WRITE(NOT,1221)
1221 F O R M A T ( / / , 5 X , * G R O U P * » 5 X , * A B S O R P T I O N ' , 5 X , »
FISSI0N»»5X,
1«
TRANSPORT',5X, •
N/FISSION',5X,•
CAPTURE'/)
00 1333
IG=1,MG
1333 W R I T E ( N O T , 1222) I G , S A 1 ( I G ) , S F 1 I I G ) , S T R K I G ) t S N U l l I G ) , S X 1 ( I G )
1 2 2 2 F O R M A T ( I H , 5X,I 3 , 7 X , 5 ( E 1 2 . 5 , 5 X ) )
WRITE(NOT,1223)
1223 F O R M A T ( / / , 5 X , « T R A N S F E R
CROSS
SECTIONS'/)
00 1 2 2 4
IG=1,MG
D O 1 2 2 4 KG= 1 »MG
1224
WRITE(NOT,1225)IG,KG,SMT1(IG,KG)
122 5 F O R M A T d H , 3 X, • G R O U P • , 13 , • T O G R O U P ' , I 3 , 5 X , E 1 2 . 5 )
220 C O N T I N U E
NEGN0=-1
W R I T E ( T O T ) N E G N O » ( K , K = 2 » 20)
G O TO 15
300 C O N T I N U E
W R I T E ( 6,300)
500 F O R M A T ( / / / , 5 X , « * * * * * E N D E D N O R M A L L Y ' )
ENÛFILE TOT
STOP
M O WRITE to, 511)
511 F O R M A T ( / / ' * * * * * W R U N G A D D I T I O N A L
ISOTOPE SPECIFIED'/
I i*****NQ
STOP «)
STOP
END
V
T
w
81
APÊNDICE
IM"
E
-
Abagyan,
L.
Referencias
P.,
culations",
et a i ,
"Group C o n s t a n t s
Consultants
for N u c l e a r R e a c t o r Cal_
Bureau E n t e r p r i s e s
I n c . , New York
(
1960).
1)4
Alcouffe,
R.E.
et a i ,
" Effect
of C o l l a p s i n g
on F a s t B r e e d e r P a r a m e t e r s " , N u c l .
Cross
Section
Data
S e i . Eng. _43 , 173-185
(
1971).
/ßf
A l l e n , W.
0. et al , " F a s t B r e e d e r R e a c t o r s w i t h Mixed Fuel
cles",
sium
IXI
Proc.
Second I n t e r n a t i o n a l
, Gatlinburg, Tenessee
Batyrebekov,
G.
A.
et a l ,
w i t h a Thorium s h i e l d " ,
Züf"
Bell,
G.
IÇ4*
Böhme, R.
et a l . ,
3"0
" Theoretical
and E x p e r i m e n t a l
Helsinki,
An
betten
vol.
Analysis
1
KeV and
16 MsV",
of F a s t
Conf. on N u c l .
427-457
of t h e N e u t r o n
Analysis
Data
(1970).
Capture
Nucl.
Sei.
Cross
Eng.
Section
3 9,
337-
(1970\
Dresner, L.,
tors",
J#f
,"
(I'V/-).
1970.
II,
6.
Reactor
" N u c l e a r R e a c t o r T h e o r y " , Van Mos -
for R e a c t o r s ,
W.
of F a s t
S o v i e t Atomic Energy 1 7 ,
Second I n t .
o f \)-IRC
Ipf
(1966).
Zero-Power A s s e m b l i e s " , Proc.
ffl' Davey,
Cycle Sympo -
" Some C h a r a c t e r i s t i c s
I. e S. G l a s s t o n e ,
trand Reinhold Co.,
Thorium Fuel
Cy_
" R e s o n a n c e A b s o r p t i o n of N e u t r o n s
Pergamon P r e s s ,
F a y a , A . J . 5 W.J.
in N u c l e a r Rea.£
1960.
Oosterkamp e S. C.
Shu-Faya,
" The Use of T h o -
riurn r'etal Blankets in F a s t B r e e d e r R e a c t o r s " , T r a n s , of t h e
ANS
]G , 181 ( 1 9 7 4 ) .
82
APÉNDICE
/J.O/'
E
( cont).
Fowler,
T.B.
et a l . ,
" N u c l e a r R e a c t o r Core A n a l y s i s
Code
:
CITATION" ORNL-TM-2496 ( 19 6 9 ) .
fiYÍ
GCFR P r o j e c t
Staff,
"300-MW(e)
tor Demonstration P l a n t " ,
lyti
Greebler,
P.
ties
et a l . ,
Gas
GA-A13045
" Implications
to Reactor Design",
Häfele, W.
et a l . ,
Hankel,
R.
V.l
-
(
et a l . ,
Hummel, H.
H.
EMf
" An E v a l u a t i o n
e Okrent, D.,
, Illinois,
1970
Kidman, R . B . e R. E.
tor Calculations",
iyfi
Kidman,
R.B.
Nucl.
Kidman
S e i . Eng.
p4/
L a n g , L. W.
of Thermal
(
on N u c l .
1970).
Review of
Coefficients'in
The American N u c l e a r
, Capítulos
Schenter,
Lar-
Society,Hins_
1 e 2.
" Group C o n s t a n t s f o r F a s t R e a c _
(
, "The S h i e l d i n g
Cross
Sections
48 ,
189-201
of
(1962).
" Reactivity
, R . B . , " An Improved
for 1DX", T r a n s ,
17-33
Conf.
A
of U-233/Thoriurn F a s t Bre¬
HEDL-TME-7136
et a l .
ting Multigroup
Int.
Uncertain
1970).
ge F a s t Power R e a c t o r s " ,
dale
-
1974).
Second.
e d e r Power R e a c t o r s " , NDA-2164-3
/IS/
(
B r e e d e r Reac
" F a s t B r e e d e r R e a c t o r s " , Annual
Nuclear Physics
[Mf
Fast
of N u c l e a r Data
Proc.
Data for R e a c t o r s , H e l s i n k i ,
/T37
Cooled
1971).
F a c t o r Method of Genera -
for F a s t Reactor Analysis
"
(1972).
F-Factor Interpolation
ANS 18 , 156-157
Scheme -
(1974).
" Power Cost R e d u c t i o n by C r o s s e d P r o g e n y
and F a s t R e a c t o r s " , Nucl , J p p l r _5
Fueling
, 302 - 309
(
1968).
/¿fl?
Leipunski,
tics
A.
I.
et a l . ,
" Improvement of P h y s i c a l
Character
of F a s t P l u t o n i u m R e a c t o r by Using U-233 and Thorium
"
83
APÊNDICE
E
(cont)
S o v i e t Atomic Energy
ijxi
Little
et
ai.
30
" Numerical
, 609 - 615 (
Comparison
for F a s t R e a c t o r s " , T r a n s ,
/*f
L o e w e n s t e i n , W.
Reactors"
B.
Uses of At.
/£3f
Maciel
En.,
, Aluisio
Report
V.6
Maciel
, Aluisio
C,
¿26?
Moore,
A.,
Gas-Cooled
A12780
(2*1
Eng.,42
of G a s - C o o l e d
89-93
(
" Status
1969)
.
of F a s t Power
of Second Conf.
Peac
"Perfil
AnalT
DNPM(
," P e r f i l
1973)
AnalT
(1973).
Fast
Reactor
Blankets"
1970).
R e p o r t on F a s t B r e e d e r Reac -
GA-10171
"A C r i t i c a l
(
1970).
E x p e r i m e n t Program for t h e
Fast Breeder Reactor-Scope-and
et a l . ,
Design
Peac.
" Some N u c l e a r and Safety
of L a r g e F a s t
Uses of At.
Oppenheim,
lations
tor"
,
, G.,
(
Codes
300-MW(e)
Purpose",
GA
(1973).
Okrent, D.
the
Proc.
" Rio de J a n e i r o , DNPM
(Why B r e e d e r s ) " ,
R.
"
C a s t a n h o e P a u l o R o b e r t o Cruz
Melese d ' H o s p i t a l
tors
/pi
Sci.
" The P h y s i c s
R a r a s " , Rio de J a n e i r o ,
" Optimization
Nucl.
144-145
Castanho e Paulo Roberto Cruz,
t i c o do U r â n i o ,
Maeder,
Processing
(1958).
t i c o do T õ r i o e T e r r a s
¿247
of Data
of ANS U ,
and D. O k r e n t ,
, A Status
1971).
C.
En.
,
e Cerbone, R.J.
on a T y p i c a l
, GA-A13108 (
Power R e a c t o r s " ,
V.12,
137-151
Considerations
Proc.
Third.
in
Conf.
(1964).
, " International
Benchmark Calcu¬
1000 MW(e) Gas Cooled F a s t B r e e d e r R e a £
1974).
84
APÊNDICE
¿307
E
(cont).
O o s t e r k a m p , W. d .
Proc.
Conf.
mics
/3T?
,
B.,
An E v a l u a t i o n of F a s t R e a c t o r B l a n k e t s "
Advanced R e a c t o r s ;
, Atlanta,
Pellaud,
11
Georgia
" Physics
/32/
Schmidt,
Proc.
J.J.,
"General
Second
. Int.
sinki,
h
I &'i
V.I,
D a v e y , W.G.
3-15
39, 337-360
;M/
USAEC D i v i s i o n
GA-10509
Status
Conf.
-
(1971).
o f N u c l e a r Data
on N u c l .
Breeder
Requirements",
Data f o r R e a c t o r
, Hel¬
(1970).
between
(
of t h e G a s - C o o l e d F a s t
Plant",
, "An A n a l y s i s
t i o n of U-238
, Design and Econo¬
( 1974).
Design
Reactor Demonstration
Physics
of t h e N e u t r o n
1 KeV and
Capture
Cross
15 M V ", N u c l .
Sec -
S c i . Eng
1970).
of R e a c t o r D e v e l o p m e n t
and T e c h n o l o g y " ,
"The
Use of Thorium in N u c l e a r Power R e a c t o r s " - WASH-1097
/,35f
W e i n b e r g , A. M . , " B u r n i n g t h e R o c k s " , ANL-6122,
Wenzel,
Fuel
mal
P.,
Cycles
White
and Thorium
-Uranium
and F a s t B r e e d e r R e a c t o r s " ,
The_r
Kernenergie
14,
(1971).
, P.H.,
Section
10-22(1959).
f o r a D e v e l o p i n g N u c l e a r Power System w i t h
Converters
231-235
/,37/
" Crossed Uranium-Plutonium
(196 9).
" Measurements
of t h e U-235 N e u t r o n
in t h e Energy Range 0.04 -
F i s s i o n Cross
14 MeV", J. N u c l .
Energy
19 , 325 ( 1 9 6 5 ) .
/38/
Wood, P . J.
and M . J.
Driscoll,
for F a s t B r e e d e r R e a c t o r s " ,
"Assesment of Thorium
C00-2250,
MITNE-148
Blankets
(1973).
Download