C o l é g i o D r u m m o n d
Educação Infantil, Ensino Fundamental, Médio e Normal e Profissional
Fone (44) 3018-2342
3018
– CIANORTE – PARANÁ
MATEMÁTICA – PROFESSOR JEAN – FUNÇÕES – 3º COLEGIAL
1. (UTFMG) Na figura, está representado
resentado o gráfico da
função f: R → R, tal que f (x) = y.
b) três horas e meia hora,
ra, respectivamente.
c)três horas e quatro horas e meia, respectivamente.
d) seis horas e três horas, respectivamente.
e) seis horas, igualmente.
3. (UFRS) A taxa de crescimento natural de uma
população é igual à diferença entre as taxas de
natalidade e mortalidade,
ortalidade, cujas evoluções estão
representadas no gráfico abaixo.
Evolução das taxas de natalidade e
mortalidade (por mil) Brasil, 1881-1993
1881
O valor da expressão E = f (3) + f (25) + f (1/√3)
pertence ao conjunto
a) { x ∈ IR / - 2 < x ≤ -1}
b) { x ∈ IR / - 1 < x ≤ 0}
c) { x ∈ IR / 1 < x ≤ 2}
d) { x ∈ IR / 0 < x ≤ 1}
e) { x ∈ IR / 2 < x ≤ 3}
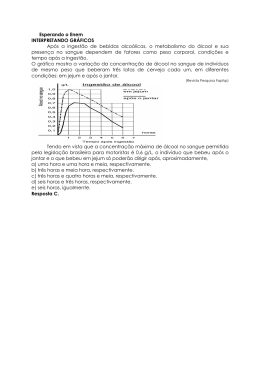
2. (ENEM) Após a ingestão de bebidas alcoólicas, o
metabolismo do álcool e sua presença no sangue
dependem de fatores como peso corporal,
condições e tempo após a ingestão.
O gráfico mostra a variação da concentração de
álcool no sangue de indivíduos de mesmo peso que
beberam três latas de cerveja cada um, em
diferentes condições: em jejum e após o jantar.
Dentre as opções abaixo, a maior taxa de
crescimento natural da população ocorreu no ano de
a) 1881.
b) 1900.
c) 1930.
d) 1955.
e) 1993.
4. (UFRN) O banho de Mafalda. Na hora do banho,
Mafalda abriu a torneira da banheira de sua casa e
ficou observando o nível da água subir. Deixou-a
Deixou
encher parcialmente para não desperdiçar água.
Fechou a torneira, entrou, lavou-se
lavou
e saiu sem
esvaziar a banheira. O gráfico a seguir que mais se
aproxima da representação do nível (N) da água na
banheira em função do tempo (t) é:
Tendo em vista que a concentração máxima de
d
álcool no sangue permitida pela legislação brasileira
para motoristas é 0,6 g/L, o indivíduo que bebeu
após o jantar e o que bebeu em jejum só poderão
dirigir após, aproximadamente,
a) uma hora e uma hora e meia, respectivamente.
C o l é g i o D r u m m o n d
Educação Infantil, Ensino Fundamental, Médio e Normal e Profissional
Fone (44) 3018-2342
3018
– CIANORTE – PARANÁ
MATEMÁTICA – PROFESSOR JEAN – FUNÇÕES – 3º COLEGIAL
5. (UFC) Na observação de um processo de síntese
de uma proteína por um microorganismo, verificouverificou
se quee a quantidade de proteína sintetizada varia
com o tempo t através da seguinte função:
a) 5 km
b) 10 km
c) 15 km
d) 20 km
e) 25 km
Q (t) = a + bt – ct2,
onde a, b e c são constantes positivas e o tempo t é
medido em minutos. Assinale a alternativa na qual
consta o gráfico cartesiano que melhor representa o
fenômeno bioquímico acima descrito.
6. (UNIOESTE) Considerando a função f, dada por
4x se 0 ≤ x < 1
f(x) =
x2 - 7x + 10 se 1 ≤ x ≤ 6
-4x + 28 se 6 < x ≤ 7
8. (PUCMG) O gráfico representa a variação da
temperatura T, medida em graus Celsius, de uma
barra de ferro em função do tempo t, medido em
minutos.
Com
base nas informações do gráfico, pode-se
pode
estimar
que a temperatura dessa barra atingiu 0°C no
instante t igual a:
a) 1 min 15 s
b) 1 min 20 s
c) 1 min 25 s
d) 1 min 30 s
e) 2 min 18 s
é correto afirmar que
01. o domínio de f(x) é o conjunto dos números
reais.
02.. o valor mínimo da função é obtido quando
x = 7/2.
04. f(1) = f(6).
08. f(f(2/3)) = -14/9.
16.. para todo x, pertencente ao domínio da função,
f(x) é maior ou igual a zero.
7. (UFSM) Sabe-se que o preço a ser pago por uma
corrida de táxi inclui uma parcela fixa, que é
denominada bandeirada, e uma parcela variável, que
é função da distância percorrida. Se o preço da
bandeirada é R$ 4,60 e o quilômetro rodado é R$
0,96, a distância percorrida pelo passageiro que
pagou R$ 19,00, para ir de sua casa ao shopping, é
de
GABARITO
1.
2.
3.
4.
5.
6.
7.
8.
c
c
d
a
e
28 (04 + 08 + 16)
c
a