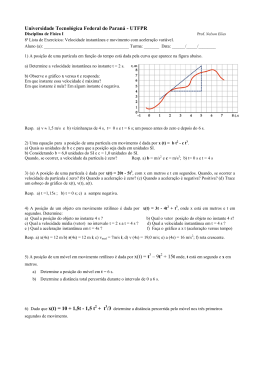
Lista 5: Derivada como taxa de variação - Cálculo Diferencial e Integral I
Professora: Elisandra Bär de Figueiredo
1. Calcule a área do triângulo retângulo ABC na Figura 1, sabendo-se que n é a reta normal a
f (x) = ex no ponto xo = 1
y
x
y=e
x
n
Figura 1: Exercício 1
2. Um forno industrial coze a temperatura constante de 608 graus centígrados. A temperatura
do forno, desde o início em que é ligado até atingir a temperatura de cozedura, é dada por:
T (t) =
20t2 + 5t + 32
, t em minutos e T (t) em ◦ C. Determine:
t+2
(a) a temperatura inicial do forno?
(b) a variação da temperatura no intervalo de tempo [2, 10].
(c) a variação instantânea da temperatura para t = 10.
3. O valor de um automóvel ao m de t anos é dado por V (t) = 50000e−0.12t , sendo V dado em reais
e t em anos.
(a) Por qual preço foi comprado o automóvel?
(b) Represente gracamente a função e determine o valor aproximado do automóvel daqui a 5
anos.
(c) A taxa de variação é negativa para qualquer valor de t. Justique esta armação e interprete
este fato no contexto da situação.
(d) Em que momento a taxa de variação é -2500 reais ao ano?
(e) Mostre que o gráco V ′ tem uma assíntota horizontal. Qual o seu signicado relativo à
situação?
4. Seja y =
√
3
3x + 2 a equação do movimento de uma partícula, determine:
(a) a velocidade da partícula quando transcorridos 2s.
(b) a aceleração da partícula quando transcorridos 2s.
(
3
)
5. Um carro está a s = 16t 2 − 24t + 16 km a leste de uma parada no instante t horas. Pergunta-se:
1
1
4
(a) Qual é a velocidade no instante t = h e qual é o sentido que ele se move?
(b) Qual a posição do carro quando sua velocidade é nula?
6. Dois corpos têm movimento em uma mesma reta segundo as equações s1 = t3 + 4t2 + t − 1 e
s2 = 2t3 − 5t2 + t + 2. Determine a velocidade e as posições desses dois corpos no instante em que
as suas acelerações são iguais. Considere s1 e s2 em metros e t em segundos.
7. Dois pontos partem da origem do eixo x no instante t = 0 e se movem ao longo desse eixo de
acordo com as equações x1 = t2 − 2t e x2 = 8t − t2 , com x1 e x2 em metros e t em segundos.
(a) Em que instante os dois têm mesma velocidade?
(b) Qual a velocidade desses pontos no instante em que eles têm a mesma posição?
8. A posição de uma partícula que se desloca ao longo do eixo y varia com o tempo x segundo a
)
v (
equação y = 0 1 − e−cx , x ≥ 0, onde v0 e c são constantes positivas. Use a DEFINIÇÃO de
c
derivadas para determinar a velocidade da partícula no instante x.
9. Uma esfera aumenta de modo que seu raio cresce a razão de 12, 5 cm/s. Qual a variação do volume
no instante em que o raio é de 15, 2 cm?
10. Dois carros, um dirigindo-se para leste com velocidade de 80 km/h, o outro dirigindo-se para
sul com velocidade de 50 km/h, estão viajando em direção ao encontro das rodovias. A que
velocidade os carros se aproximam um do outro, no momento em que o primeiro carro está a 400
m e o segundo está a 300 m da interseção das rodovias?
11. Um tanque de forma cônica invertido tem altura de 8 m, raio da base 2 m. O mesmo se enche de
água à razão de 7 m3 /min. Com que velocidade sobe o nível da água quando este se encontra a
4 m de profundidade?
12. Uma piscina tem 18 m de largura, 28 m de comprimento, 2 m de profundidade em um extremo e
8 m no outro, o fundo tem forma de um plano inclinado. Se a água está sendo bombeada para a
piscina à razão de 0, 8 m3 /min, com que velocidade se eleva o nível da água no instante em que
ele esta a 1, 8 m na extremidade mais profunda?
13. Em que pontos da parábola y 2 − 18x = 0 a ordenada y cresce duas vezes mais depressa que a
abscissa x?
14. Uma criança esta empinando uma pipa e movendo-se horizontalmente a 4 m/s. Supondo que a
pipa permaneça sempre a 80 m de altura, sobre o nível do solo, qual é a velocidade com que a
criança está soltando a corda da pipa quando esta corda medir 100 m?
Obs : Despreze a altura da criança.
15. Um tanque tem a forma de um cilindro circular reto com raio da base de 5 m e altura de 10 m.
Se instante t = 0s, a água começa a uir no tanque à razão de 25 m3 /h, determine:
(a) com que velocidade sobe o nível da água?
(b) quanto tempo levará para encher o tanque?
16. Um balão está subindo verticalmente acima de uma estrada a uma velocidade constante de
1
m/s. Quando ele está a 17 m acima do solo, uma bicicleta que se desloca a uma velocidade
3
constante de 5 m/s passa por baixo dele. A que taxa a distância entre a bicicleta e o balão
aumentará 3s depois?
2
17. O nível de café que escoa de um ltro cônico, de diâmetro e altura 15 cm, para uma cafeteira
cilíndrica, de diâmetro e altura 15 cm, varia a uma taxa de 2 · 10−4 cm/min. A que taxa o nível
do café, na cafeteira, aumentará quando a altura de café no ltro for 5 cm?
18. Um cabo de cobre tem diâmetro de 1 cm a 0◦ C . Suponha que seu comprimento é de 1 m e não se
altera com a variação da temperatura. Se seu diâmetro aumenta a uma velocidade de 0, 02cm/◦ C,
Calcule a taxa de variação do volume desse cabo quando a temperatura está a 20◦ C .
19. Numa granja de frangos, o abastecimento de ração é automático. A ração está num reservatório
que tem a forma de uma pirâmide de base quadrada com 2 m de lado e 6 m de altura, cujo vértice
está voltado para baixo. Se o consumo de ração é de 0, 05 m3 /h, com que velocidade desce o nível
de ração quando este está a 2 m do vértice?
20. A altura de um triângulo cresce a razão de 1cm/ min e sua área aumenta a razão de 2cm2 / min.
Qual a taxa de variação da base do triângulo quando sua altura for 10cm e sua área 100cm2 .
21. Uma piscina tem 24m de comprimento e seus extremos são trapézios isósceles com altura de 6m,
uma base menor 6m e uma base maior de 8m. A água está sendo bombeada para a piscina à
razão de 10m3 /mim. Com que velocidade o nível de água está subindo quando a profundidade
da água é de 2m?
22. Um avião (A) voa a 124 m/s, paralelamente ao solo, a uma altitude de 1220 m no sentido oeste,
tomando como referência um holofote (H), xado no solo, que o focaliza e que se encontra à
esquerda da projeção vertical (P) do avião e sabendo que a luz do holofote deverá permanecer
iluminando o avião, qual será a velocidade com que θ estará variando quando a distância entre o
holofote e a projeção vertical do avião for de 610 m?
23. Às 7 : 00 horas dois navios partem de um ponto O em rotas que formam um ângulo de 120◦ . Os
navios A e B deslocam-se a 20 km/h e 25km/h, respectivamente. Determine qual é a velocidade
de afastamento desses navios às 9 : 00 horas.
Respostas:
1. A =
e3
u.a.
2
2. .
(a) 16◦ C.
(b) 17,875◦ C.
(c) 19,29◦ C por minuto.
3. .
(a) 50000 reais.
(b)
(c)
(d) 7,3 anos.
(e)
1
4
4. (a) v(2) = u.c./s
(b) a(2) = −
1
u.c./s2
16
5. (a) v(1/4) = −12km/h e está indo na direção oeste
3
(b) s(1) = 8km
6. t = 3s; v1 (3) = 52m/s; v2 (3) = 25m/s; s1 (3) = 65m; s2 (3) = 14m
7. (a) 2,5s
(b) t = 0s ⇒ v1 = −2cm/s e v2 = 8cm/s; t = 5s ⇒ v1 = 8cm/s e v2 = −2cm/s
8. v0 e−cx u.c./u.t.
9. 11552π cm3 /s
10. 94km/h
11.
7
m/min
π
12. 0,005m/min ou 0,025m/min, dependendo da interpretação da piscina.
(
13.
9 9
,
8 2
)
14. 2,4m/s
15. (a)
1
m/h
π
(b) 31,4h
27
≈ 3, 46m/s
61
16. √
17.
2 · 10−4
cm/min
9
18. 1, 4π cm3 /min
19. -0,1125m/h
20. -1,6cm/min
21. 0,0625m/min
22. 0,08rad/s
√
23. 5 61km/h
4