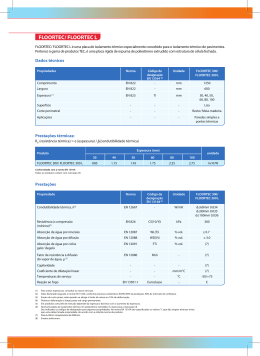
Portfolio de:
Problema motivador 01:
qual a função da camada de material polimérico
colocada sobre fios elétricos de cobre ou de alumínio?
Problema motivador 02:
qual a espessura da camada de tijolos de uma parede
de modo a melhor isolar termicamente uma casa?
Problema motivador 03:
qual a espessura de isolamento térmico sobre uma
linha de vapor de modo a minimizar perdas
energéticas?
O raio crítico
(adaptado do exemplo 3.4 de Incropera & De Witt, p. 51-4a Edição, p. 72-5a edição)
A possível existência de uma espessura ótima para a camada de isolamento térmico em
sistemas radiais é sugerida pela presença de efeitos concorrentes associados ao aumento
dessa espessura. Em particular, embora a resistência à condução de calor aumente com a
adição de isolamento térmico, a resistência térmica à convecção de calor diminui devido
ao aumento da área superficial externa. Dessa forma, deve existir uma espessura da
camada de isolamento térmico que minimize a perda de calor pela maximização da
resistência total à transferência de calor. Resolva esse problema levando em
consideração o seguinte sistema.
1. Considere um tubo delgado de cobre com raio ri cuja superfície se encontra a uma
temperatura Ti menor do que a temperatura do ambiente T∞ ao redor do tubo. Existe
uma espessura ótima associada à aplicação de uma camada de isolamento térmico
sobre o tubo?
2. Confirme o resultado acima calculando a resistência térmica total, por unidade de
comprimento do tubo em um tubo com 10 mm de diâmetro que possui as seguintes
espessuras de isolamento térmico: 0, 2, 5, 10, 20 e 40 mm. O isolamento é composto
por vidro celular, e o coeficiente de transferência de calor por convecção em sua
superfície externa é de 5W/m2K.
UPM/EE/DEM/FT-II-5C/Profa. Dra. Míriam Tvrzská de Gouvêa/2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/Profa. Dra. Esleide Lopes Casella/2004-2S
93
Portfolio de:
solução
figura – esquema do problema (Incropera & De Witt, p. 51)
das condições do problema (sem geração de calor e regime permamente) – qr=constante
hipótese adicionais: desprezada troca de calor por radiação
donde:
qr =
1
(Ti − T∞ )
Rtot
com:
r
1
ri
+
Rtot =
2π k 2π rh
ln
para uma espessura r-ri:
espessura ótima
dRtot
d 2 Rtot
dqr
d 2 qr
= 0; 2 < 0 ⇔
= 0;
>0
dr
dr
dr
dr 2
⇒
1
1
k
−
=
⇒
=
0
r
2π kr 2π r 2 h
h
logo:
condição de 2a ordem – verificação de máximos/mínimos:
r=
k
h h2
d 2 Rtot
1
1
=
−
+
=
>0 ⇒
dr 2
2π kr 2 π r 3h 2π k 3
trata-se de ponto de máxima taxa de
transferência de calor (ponto de
mínimo na curva Rtot × r)
Ou seja, a máxima perda de calor se dá para
r = rc =
k
, r é chamado de raio crítico.
h c
UPM/EE/DEM/FT-II-5C/Profa. Dra. Míriam Tvrzská de Gouvêa/2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/Profa. Dra. Esleide Lopes Casella/2004-2S
94
Portfolio de:
Assim, em termos de uma perda de calor, não existe uma espessura ótima de
isolamento, uma vez que o que se deseja é que não haja perda de calor!
Temos as seguintes características no sistema radial:
•
•
•
aumentando-se r até rc a perda de calor aumenta até o valor máximo
aumentando-se r após rc a perda de calor diminui até zero para r → ∞
se rc < ri o aumento do isolamento traz sempre uma diminuição da perda de calor
para o problema em pauta:
rc = 0.011(m) > ri = 0.01(m) - logo teremos o seguinte comportamento:
figura – comportamento da resistência térmica de transferência de calor em função da espessura
(Incropera & De Witt, p. 52)
figura – comportamento do fluxo/taxa de calor (extraída das notas de aula do Prof. Oliveira)
UPM/EE/DEM/FT-II-5C/Profa. Dra. Míriam Tvrzská de Gouvêa/2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/Profa. Dra. Esleide Lopes Casella/2004-2S
95
Portfolio de:
Observações:
1. para fios/cabos elétricos – o revestimento funciona como um dissipador de calor,
assim é de interesse que
ri < rc de modo que se escolha uma espessura de
revestimento tal que se tenha r = rc , quando a máxima dissipação de calor irá
ocorrer.
2. Para o projeto do revestimento de cabos elétricos, têm-se como parâmetros o
material do isolamento (que afeta o valor de k) e o coeficiente de troca térmica
(modificação do fluido em contato com o ar ou a introdução de convecção forçada
ao invés da natural)
3. "A existência de um raio crítico exige que a área de transferência de calor varie na
direção da transferência, como é o caso da condução radial em um cilindro (ou em
uma esfera). Em uma parede plana, a área normal à direção da transferência de calor
é constante, não havendo uma espessura crítica para o isolamento térmico (a
resistência total sempre aumenta com o aumento da espessura do isolamento)."
(Incropera & De Witt, p. 52-4a edição, p.73-5a edição)
leitura recomendada:
Kreith:
Braga:
p.106-107
Exemplo recomendado para leitura:
Brodkey & Hershey:
Incropera & De Witt:
Kreith:
Braga:
exemplo 11.4, p. 503
exemplo 3.4 (comentários)
exercício resolvido 3 (p.109-111)
Exercícios básicos recomendados da lista: 3.43; 3.47; 3.53 (Incropera ; De Witt, 5° edição)
Exercícios:
Exercício 01:
mostrar que a expressão para o raio crítico em um sistema composto
de duas esferas concêntricas (a externa sendo o isolante) é rc=2k/h
Este raio crítico se refere a um ponto de máxima, mínima
transferência de calor ou a um ponto de inflexão? Qual a sua
utilidade?
UPM/EE/DEM/FT-II-5C/Profa. Dra. Míriam Tvrzská de Gouvêa/2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/Profa. Dra. Esleide Lopes Casella/2004-2S
96
Portfolio de:
Exercício 02:
Existe uma espessura ótima de um isolamento térmico? Justifique.
Exercício 03:
Um material B de condutividade 0.046 (SI) e espessura 1mm é
colocado externamente a um cilindro de 4mm de diâmetro externo,
cuja superfície está a 60oC. O arranjo troca calor com ar ambiente e
sabe-se que o coeficiente de convecção com o ar é de 10 (SI). O
material B está atuando como um isolante térmico ou como um
dissipador de calor? Justifique.
Exercício 04:
Um condutor elétrico é constituído por longo cilindro de cobre
recoberto por uma camada de isolamento. O fio de cobre tem 3mm
de diâmetro. O isolamento tem uma temperatura máxima permissível
de 90oC e uma condutividade térmica de 0.251W/moC. O ar
circunjacente está a 58oC de temperatura média (coeficiente de
convecção de 15 W/ m2oC). Pede-se:
a-) Para o sistema descrito, calcular a espessura do isolamento que
permite a máxima perda de calor, bem como o calor dissipado.
Justificar a resposta.
b-) Para o sistema descrito em 1, descrever o que deveria mudar no
sistema para que o isolamento funcione efetivamente como um
isolante térmico e não como um dissipador de calor.
UPM/EE/DEM/FT-II-5C/Profa. Dra. Míriam Tvrzská de Gouvêa/2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/Profa. Dra. Esleide Lopes Casella/2004-2S
97
Portfolio de:
Exercício 05: (3.47 Incropera) Uma corrente elétrica de 700A flui através de um cabo
de aço inoxidável de diâmetro 5 mm e resistência elétrica de 6x10-4 Ω/m. O cabo
encontra-se em um ambiente que está a uma temperatura de 30°C e o coeficiente total
de transferência de calor (associado à convecção e à radiação) entre o cabo e o ambiente
é de 25 W/m2.K. Pede-se:
a) se o cabo estiver desencapado, qual será a temperatura na superfície do cabo?
b) se um revestimento delgado de um isolante elétrico for aplicado sobre o cabo
com uma resistência térmica de 0,02m2.K/W, quais serão as temperaturas das
superfícies do cabo e do isolamento? serão iguais?
c) Há uma preocupação com relação à capacidade do isolamento de suportar
elevadas temperaturas. Qual deve ser a espessura do isolamento que fornecerá a
menor das temperaturas máximas possíveis para o isolamento? E qual será o
valor dessa temperatura ? e da superfície do cabo?
dado: condutividade térmica do isolante k=0,5 W/m.K
Resp.
a)Tc=778,7°C b)Tc=1153°C;Tisol=778,7°C c)e=0,0175m;Tisol=318,2°C;Tc=692,5°C;
UPM/EE/DEM/FT-II-5C/Profa. Dra. Míriam Tvrzská de Gouvêa/2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/Profa. Dra. Esleide Lopes Casella/2004-2S
98