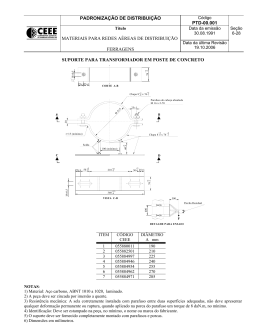
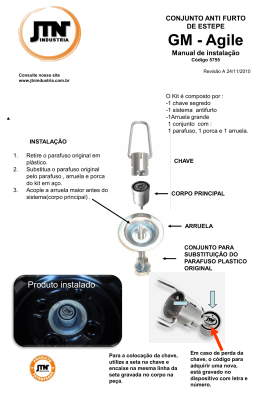
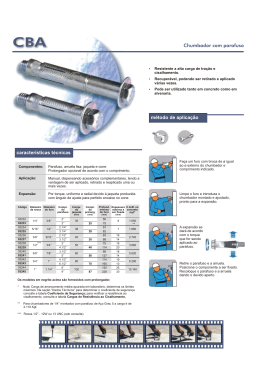
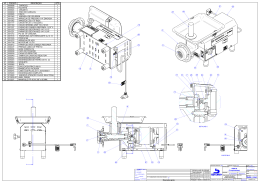
▼
Questão 37
O projeto de uma ferramenta prevê que ela se encaixe perfeitamente em um parafuso de cabeça hexagonal
regular, como indica a figura.
Cabeça da ferramenta
λ
Braço da ferramenta
y
y
Parafuso
x
x
a) Calcule as medidas de x e y, admitindo a medida do lado do hexágono que forma a cabeça do parafuso
igual a 2 cm.
b) Considere λ como um arco de circunferência cujo centro é o ponto médio do segmento de comprimento y,
indicado no projeto da ferramenta.
Sendo L a medida do lado do hexágono que forma a cabeça do parafuso, e R a medida do raio de λ , determine R em função de L.
Resolução
Sendo L a medida do lado do hexágono regular, temos a figura:
C
y
L
2
M
O
L
2
B
A
L
x
Como AOB e COB são triângulos eqüiláteros de lado L, temos:
AM = MC =
x=L +
Logo:
L 3
.
2
L
3L
∴ x=
2
2
(I)
e
y = AM + MC
L 3 L 3
(II)
+
∴ y=L 3
2
2
a) Sendo L = 2 cm segue, de (I) e (II), que:
y=
x = 3 cm e y = 2 3 cm
Resposta: x = 3 cm e y = 2 3 cm
1
λ
b)
y
2
R
y
2
x
Aplicando o teorema de Pitágoras no triângulo retângulo destacado, temos:
 y 2
R2 = x2 +  
 2
(III)
De (I), (II) e (III), segue:
2
 3L 2  L 3 


R =   +
 2 
2


2
R2 =
9L2 3L2
+
∴ R=L 3
4
4
Resposta: L 3
2