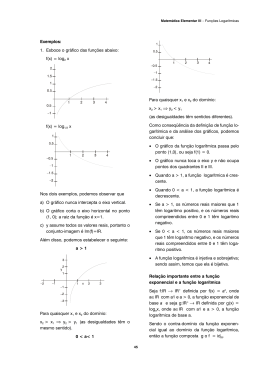
CAMPUS
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E
TECNOLOGIA DE SÃO PAULO
Sertãozinho
PLANO DE ENSINO
1 – IDENTIFICAÇÃO
Curso:
Modalidade de Ensino:
Licenciatura em Química
Superior - Licenciatura
Componente Curricular:
Código:
Matemática Básica
MTB
Área:
Ano/Semestre:
Química e Ciências
Aulas semanais:
03
1º/ 2010
Total de Aulas:
114
Total de Horas:
85,5
Nº de Professores:
01
Professores Responsáveis:
Luiz Carlos Leal Junior
2 – OBJETIVOS
Este componente curricular tem como objetivo consolidar e ampliar conteúdos de
matemática vistos na educação básica, tanto no ensino fundamental quanto médio,
preparando o aluno para trabalhar com esta ferramenta nos cálculos necessários aos
demais componentes curriculares.
3 – EMENTA
Operações com os números reais. Potenciação.
Funções elementares e funções reais de uma variável: funções de 1º e 2º graus, função
exponencial, função logarítmica, funções trigonométricas.
Introdução ao conceito de limite de uma função.
4 –CONTEÚDO PROGRAMÁTICO
1. Operações com números reais.
• Conjuntos numéricos: números naturais, inteiros, racionais e reais.
• Potenciação e radiciação.
• Potências de base 10 e a notação científica.
2. Introdução ao Estudo de Funções
• Relação entre grandezas variáveis.
• Definição e notação de funções.
• Domínio e imagem.
• Gráficos de uma função.
• Crescimento e decrescimento.
3. Função de 1º Grau
• Definição da função de 1º grau.
• Gráficos das funções de 1º grau.
• Crescimento, domínio, imagem, zeros (raízes) e estudo do sinal.
4. Função do 2º Grau
• Definição da função do 2º grau.
• Gráficos da função de 2º grau.
• Crescimento, concavidade, domínio, imagem, zeros (raízes) e estudo do sinal.
• Vértice, pontos de máximo e mínimo.
5. Função Exponencial
• Definição da função exponencial.
• Gráficos da função exponencial.
• Crescimento, concavidade, domínio, imagem, zeros (raízes) e estudo do sinal.
6. Função Logarítmica
• Definição da função logarítmica.
• Gráficos da função logarítmica.
• Crescimento, concavidade, domínio, imagem, zeros (raízes) e estudo do sinal.
7. Funções Trigonométricas
• Função seno: definição, gráfico, e análise da função seno.
• Função cosseno: definição, gráfico, e análise da função cosseno.
• Função tangente: definição, gráfico, e análise da função tangente.
• Função cotangente: definição, gráfico, e análise da função cotangente.
• Função secante: definição, gráfico, e análise da função secante.
• Função cossecante: definição, gráfico, e análise da função cossecante.
8. Limite
• Assíntotas verticais e horizontais.
• Definição de limite.
• Interpretação gráfica do limite.
•
Limite de uma função.
5 – METODOLOGIA E ESTRATÉGIAS DE ENSINO
Os conceitos e teorias serão abordados em aulas expositivo-dialógicas, priorizando a
participação ativa do aluno com questionamentos e discussões. Sendo utilizado algum
software matemático para estudo de alguns assuntos.
Os cálculos serão trabalhados com a resolução de problemas e exercícios, individualmente e
em grupo, com posterior correção e solução de dúvidas.
Eventualmente serão feitos seminários de conteúdos já trabalhados em classe buscando
uma aplicação com a área de estudo.
6 – RECURSOS DIDÁTICOS
• Lousa e caneta para quadro branco.
•
Retroprojetor
•
Materiais para construção de gráficos: régua, papel milimetrado, etc.
•
Software matemático.
7 – CRITÉRIOS DE AVALIAÇÃO / RECUPERAÇÃO PARALELA / INSTRUMENTO FINAL
DE AVALIAÇÃO
Provas escritas: P1 e P2, dos 1º e 2º semestre, respectivamente.
Atividades para nota: A1 e A2 (listas de exercícios, exercícios em sala de aula ou seminários)
dos 1º e 2º semestre, respectivamente.
0,7
0,3
Nota Final =
( A1 + A2 )
( P1 + P2 ) +
2
2
A nota final do componente curricular será a média aritmética das notas semestrais.
Não haverá recuperação paralela. O instrumento final de avaliação será uma prova escrita.
Todos os rendimentos serão regidos conforme as Normas Acadêmicas do Ensino Superior do
IFSP.
As notas semestrais serão regidas pela seguinte fórmula: Semestre N, N=1,2.
Nota do Semestre N = 0,7 xPN + 0,3 xAN
8 – BIBLIOGRAFIA
a) Básica:
12-
MEDEIROS, V.Z. Pré-cálculo. 1. ed. Rio de Janeiro, Thomson, 2005.
DEMANA, F. WAITS, B. FOLEY, G. KENNEDY, D. Pré- Cálculo. SP. Addison
Wesley, 2008.
b) Complementar:
1-
2-
3-
4-
5-
IEZZI, G. Fundamentos de matemática elementar. Vol 1: conjuntos e funções. São
Paulo, Atual, 2004.
IEZZI, G. Fundamentos de matemática elementar. Vol 2: Exponenciais e
Logarítmos. São Paulo, Atual, 2004.
IEZZI, G. Fundamentos de matemática elementar. Vol 8: Noções de limite, derivada
e integral. São Paulo, Atual, 2004.
LIMA, E. L. et al. A matemática do ensino médio – Vol. 1. 5. ed. Rio de Janeiro,
SBM, 2000.
_______, Matemática: Construção e Significado, Vol. 1, 2 e 3. São Paulo, Ed.
Moderna, 2008.
Professor(es)
Coordenador de Área /
Curso
Gerente Acadêmico