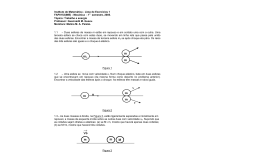
Experimento 6
Colisões em duas dimensões
A. Turtelli
Neste experimento será estudado o choque não frontal (choque de raspão) entre uma
esfera em movimento e outra em repouso, em um plano horizontal. As medidas obtidas
serão analisadas no Referencial Laboratório.
Com esta experiência (a mais importante do curso) vamos estudar um fenômeno muito
comum no nosso dia a dia: as colisões, os choques, as interações. Colisões ou, de uma
maneira mais geral, interações são um dos fenômenos mais comuns no nosso dia a dia e
são o mecanismo através do qual o ser humano se comunica com o mundo ao seu redor e
se insere no seu meio ambiente.
Nas inter-ações, como a própria etimologia da palavra indica, uma ação qualquer acontece entre dois ou mais corpos, uma informação qualquer é trocada entre eles. Qualquer
tentativa de entender e de medir caracterı́sticas do universo que nos cerca, tanto no microcosmo como no macrocosmo, também é uma interação. Qualquer medida que se faça
é uma interação, na qual ou o aparelho de medida, ou o observador, ou ambos, interagem
com o objeto (fenômeno) a ser medido (analisado).
É esse o fenômeno que estudaremos. Qual o modelo que construiremos para tentar
explicá-lo? Vamos restringir o objeto de nosso estudo à interação, colisão, entre apenas
dois corpos além de tudo vamos supor que não haja nenhuma ação de qualquer outro
corpo influenciando essa inter-ação entre os dois corpos considerados.
Com base no que já vimos até agora nesse nosso curso, podemos afirmar que o estado
de movimento de um conjunto dos dois corpos (corpo 1 e corpo 2) não irá se alterar, já
que não há nenhuma ação externa ao sistema (o conjunto dos dois corpos) sendo exercida
sobre ele.
Portanto, como não há nada agindo sobre eles a partir de fora, devemos esperar que o
estado de movimento deles não se alterará. Ou seja, o quanto eles têm de movimento não
muda. Isso, em uma linguagem mais técnica, significa: a quantidade de movimento total
se conserva. A energia total também se conserva sempre, mas não a energia cinética, que
só se conserva em certo tipo de choque, chamado choque elástico.
É difı́cil testar esse modelo em laboratório, pois sempre existem forças de atrito, que
mascaram o resultado final. Como a força de atrito é uma força de contato, se fosse
possı́vel efetuar o choque no ar e analisar as trajetórias antes e depois do choque também
no ar, os efeitos das forças de atrito seriam reduzidos praticamente a zero. Isso porque
a única força dissipativa neste caso seria a resistência do ar, totalmente desprezı́vel se as
velocidades forem baixas e as trajetória curtas. A figura a seguir mostra como se consegue
efetuar o choque no ar e medir as velocidades.
A esfera 1 desce a canaleta e no fim dela terá velocidade apenas horizontal. Essa
velocidade antes do choque pode ser medida através do alcance da esfera 1, marcado
quando ela bate na mesa sem colidir com a esfera 2. Após o choque, as velocidades das
duas esferas também serão medidas pelos seus alcances.
Como antes do choque só havia quantidade de movimento horizontal (a esfera incidente
sai da canaleta com velocidade apenas na horizontal), é a quantidade de movimento nessa
direção que deve ser conservada e essa pode ser facilmente medida usando o alcance
horizontal da esfera 1 e seu tempo de queda.
Através dos resultados obtidos será possı́vel verificar se foram conservadas a quantidade de movimento e a energia cinética e também calcular a elasticidade do choque.
1
Figura 1: Parte final da rampa de lançamento com um suporte metálico onde se coloca a
esfera alvo. O suporte é fixado na canaleta de modo a poder girar, possibilitando alterar
o parâmetro de impacto do choque
Material Utilizado
• Rampa de lançamento
• 3 esferas de aço - duas delas com massas iguais e a terceira com massa diferente das
primeiras
• Prumo de linha
• Nı́vel de bolha
• Régua
• Balança digital
• 2 cartolinas brancas
• Papel carbono
Procedimento
A rampa é utilizada para garantir que a esfera incidente tenha sempre a mesma velocidade
antes do choque, desde que solta sempre do mesmo lugar. O alcance máximo depende
da velocidade horizontal do corpo, que é constante porque não há força resultante nessa
direção. Portanto, se soltamos a esfera de um certo ponto da canaleta e deixamos ela cair
na mesa, a distância entre a projeção do fim da canaleta (use o prumo de linha) até o
ponto de impacto é proporcional à velocidade.
2
Como a esfera incidente tem apenas velocidade na direção horizontal e o choque se
dá em um plano horizontal (o plano que contém os centros das duas esferas), a esfera
alvo também receberá dela apenas velocidade na direção horizontal, consequentemente, a
distância entre o ponto onde ela caiu na mesa até a projeção do suporte onde ela estava
é proporcional à sua velocidade após a colisão. E a distância entre o ponto onde a esfera
incidente bate na mesa após o choque até a projeção do fim da canaleta é proporcional
à sua velocidade após o choque. Portanto, marcando-se esses pontos e medindo-se as
distâncias, pode-se testar o modelo fı́sico do choque em duas dimensões, verificando as
leis de conservação.
As posições das esferas em um determinado instante serão marcadas utilizando-se o
movimento vertical. O tempo de queda poderá ser determinado facilmente medindo-se
h ± ∆h.
Antes de iniciar as medidas, meça as massas das três esferas que você vai utilizar.
Comece fazendo alguns lançamentos com e sem choque para regular a melhor altura
do fim da canaleta em relação à mesa, para evitar que alguma das esferas caia fora da
cartolina utilizada para marcar os pontos. Convém que a altura da qual a esfera é solta
(acima da parte horizontal da canaleta) não seja muito grande e também que a altura
do fim da canaleta em relação à mesa não seja muito alta. Assim minimizando os efeitos
de eventuais irregularidades na canaleta, obtém-se uma melhor distribuição dos pontos
experimentais na cartolina. Se esses efeitos fossem iguais para cada lançamento, eles
não seriam importantes para o estudo que se quer fazer. Mas eles podem variar a cada
lançamento e por isso convém reduzir o percurso da esfera sobre a canaleta.
As medidas serão feitas com esferas de massas iguais e depois (com outra cartolina)
com esferas de massas diferentes. Em ambos os casos serão selecionados 5 parâmentros
de impacto diferentes (isso é, 5 posições diferentes da esfera alvo), dispostos razoalvelmente espaçados e dos dois lados da canaleta. Procure alinhar cuidadosamente os
centros de massa das duas esferas na mesma horizontal e sempre evitar que o centro de
massa da esfera alvo esteja para trás do centro de massa da esfera incidente. Para cada
parâmentro serão feitos 5 lançamentos.
Em nossa convenção, ”1” é a esfera incidente e ”2” a esfera alvo. Marque as origens:
O1 é a origem para a esfera incidente (a projeção na mesa do fim da canaleta), O2 é a
origem para a esfera alvo (a projeção na mesa do pino onde o alvo está apoiado, marque
esse ponto cuidadosamente usando o fio de prumo fixado no pino).
1. O segmento O1i é proporcional à velocidade inicial (antes do choque) da esfera
incidente,
2. Os segmentos O1j (j variando de 1 até 5) são proporcionais às velocidades finais
(depois do choque) da esfera incidente, para os parâmentros de impacto de 1 até 5
(cada j é a posição média de cada um dos 5 lançamentos, para cada parâmetro de
impacto),
3. Os segmentos O2j (j variando de 1 até 5) são proporcionais às velocidades finais
(depois do choque) da esfera alvo, para os parâmetros de impacto de 1 até 5 (as
posições médias dos 5 lançamentos para cada parâmetro de impacto j ).
Marque cuidadosamente na cartolina todos os pontos de impacto, seguindo a convenção
acima. Só coloque o carbono após efetuar alguns lançamentos e ter uma idéia de onde as
esferas cairão. Use pedaços pequenos de carbono, só nos pontos de impacto previamente
3
estimados, para possibilitar uma melhor visão do conjunto. A figura 2 mostra um exemplo
da marcação de um conjunto de 5 lançamento para um parâmetro de impacto.
Se fossem feitos infinitos lançamentos para um parâmetro de impacto, terı́amos as
posições marcadas na cartolina circunscritos à dois circulos, um para cada esfera. Estes
cı́rculos ocorrem devido ao erro estatı́stico na direção x e y. Neste caso podemos considerar
que o centro do cı́rculo que circunscreve um conjunto de marcas corresponde ao valor
médio da posição de choque (x, y) daquela esfera. Além disso, o raio do cı́rculo seria o
valor do erro associado ao valor de x e y, conforme mostrado na figura 2.
Figura 2:
Relatório
(Sempre que for o caso, os itens devem ser respondidos para as medidas com esferas de
massas iguais e diferentes)
1. Demonstre claramente que os segmentos O1j e O2j são proporcionais às velocidades
depois do choque e O1i à velocidade da esfera incidente antes do choque. Determine
numericamente a(s) constante(s) de proporcionalidade.
2. Encontre o tempo de queda t ± ∆t em função de h ± ∆h usando a aceleração da
gravidade g = 10.0 ± 0.2 m/s2
4
3. Determine os vetores velocidade ~v de cada esfera antes e depois do choque para cada
parâmetro de impacto. Use os formatos:
~v = (vx ± ∆vx ) î + (vy ± ∆vy )ĵ
4. Determine os vetores quantidades de movimento p~ de cada esfera antes e depois do
choque usando o resultado do item 3 e m ± ∆m de cada esfera:
p~ = (px ± ∆px ) î + (py ± ∆py )ĵ
5. Determine graficamente, na cartolina ou em uma cópia dela, o vetor velocidade
relativa de aproximação antes do choque ~v1i − ~v2i e o de afastamento depois do
choque ~v2f − ~v1f , para três parâmetros de impacto diferentes,
6. A partir dos resultados do item 5, você pode concluir alguma coisa a respeito do
tipo de choque?
7. O sistema das duas esferas pode ser considerado um sistema isolado na análise do
choque? E a força gravitacional, não é uma força externa?
8. Para dois casos de parâmetros de impacto, faça um estudo detalhado da conservação
de quantidades de movimento antes e depois do choque, incluindo análise de erro.
Para os demais casos, mostre simplesmente se houve ou não conservação.
9. Para dois casos de parâmetros de impacto, faça um estudo detalhado da conservação
da energia entre o fim da canaleta (logo antes do choque) e o instante em que as
esferas tocam na mesa, quando ambas têm velocidades também na direção z.
5