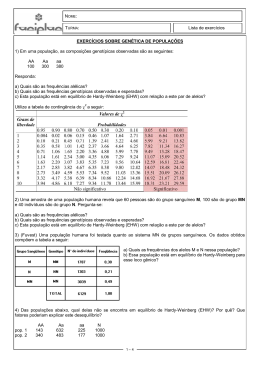
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
UM JOGO DE BOLINHAS: ENTENDENDO O TEOREMA DE HARDY-WEINBERG
Alan Bonner da Silva Costa (Laboratório de Genética Marinha e Evolução - Departamento
de Biologia Marinha - Instituto de Biologia - UFF - Bolsista PROGRAD)
Edson Pereira da Silva (Laboratório de Genética Marinha e Evolução - Departamento de
Biologia Marinha - Instituto de Biologia - UFF)
RESUMO
Jogos didáticos têm como função facilitar o aprendizado de conteúdos escolares. No presente
trabalho é apresentada uma proposta de jogo didático para auxiliar o aprendizado dos
conceitos envolvidos no teste da hipótese de equilíbrio de Hardy-Weinberg, bem como
resultados da sua avaliação por parte de alunos universitários. O Teorema de Hardy-Weinberg
tem sido apontado, por professores e alunos, como um dos temas de maior dificuldade tanto
de ensino, quanto de aprendizagem em relação à teoria evolutiva. Desta forma, espera-se que
a apresentação deste jogo e dos resultados positivos da sua avaliação desperte o interesse de
professores para reproduzir esta atividade em suas aulas de genética e evolução.
Palavras-chave: jogos didáticos, ensino de evolução, equilíbrio de Hardy-Weinberg
98
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
UM JOGO DE BOLINHAS: ENTENDENDO O TEOREMA DE HARDY-WEINBERG
Alan Bonner da Silva Costa (Laboratório de Genética Marinha e Evolução - Departamento de
Biologia Marinha - Instituto de Biologia - UFF - Bolsista PROGRAD)
Edson Pereira da Silva (Laboratório de Genética Marinha e Evolução - Departamento de
Biologia Marinha - Instituto de Biologia - UFF)
INTRODUÇÃO
O Teorema de Hardy-Weinberg foi postulado no início do século XX pelo matemático
inglês Godfrey Harold Hardy e pelo médico alemão Wilhelm Weinberg de maneira
independente (HARDY, 1908; WEINBERG, 1908). Esta hipótese propõe que as frequências
gênicas de uma determinada população permanecerão constantes ao longo das gerações,
independentemente das frequências iniciais, se não houver a ação de nenhuma das forças
evolutivas (SENE, 2008).
O Teorema de Hardy-Weinberg possui diversas utilidades no trabalho com genética de
populações como, por exemplo, sugerir se uma força evolutiva está agindo sobre as
frequências de um dado lócus em uma população (DOBZHANSKY & LEVENE, 1948;
KERR & WRIGHT, 1954), estimar coeficientes de endogamia, identificar de erros de
amostragem, entre outros (FUTUYMA, 2009).
A despeito de sua importância em genética de populações, o ensino do Teorema de
Hardy-Weinberg no ensino básico e superior enfrenta resistências (MERTENS, 1992). Em
pesquisa sobre o ensino da teoria evolutiva em escolas brasileiras, Tidon & Lewontin (2004)
relataram que os professores consideram os conteúdos relacionados a frequências alélicas e ao
Teorema de Hardy-Weinberg como os mais difíceis de ensinar dentre os conceitos que
envolvem a evolução biológica.
O presente trabalho se dedica a apresentar um jogo didático no qual o Equilíbrio de
Hardy-Weinberg é testado para populações artificiais. Os jogos didáticos têm sido apontados
como importantes ferramentas de auxilio a aprendizagem de conceitos científicos (GRIFFITH
& MAYER-SMITH, 2000; KRASILCHIK, 2008). Desta forma, pretende-se contribuir para o
ensino-aprendizagem deste conteúdo em sala de aula por professores e alunos.
Esta atividade faz parte do programa de aulas práticas da disciplina “Evolução” do
curso de graduação em Ciências Biológicas da Universidade Federal Fluminense. Além da
apresentação do jogo, este trabalho traz também os resultados da avaliação que os estudantes
fazem ao término da disciplina sobre esta atividade.
99
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
MATERIAL NECESSÁRIO
Para o jogo, serão necessários os seguintes materiais:
1) 300 bolinhas pretas (as bolinhas podem ser de qualquer cor, desde que a metade do total
delas seja de cor diferente da outra metade);
2) 300 bolinhas brancas (as bolinhas podem ser de qualquer cor, desde que a metade do total
delas seja de cor diferente da outra metade);
3) 3 sacos opacos;
4) Roteiro de atividades (descrito em “Roteiro de Atividades”).
CONSTRUÇÃO DO JOGO
As bolinhas deverão ser divididas entre os três sacos opacos de forma a representar 3
populações com 200 alelos (cada alelo representado por uma bolinha, portanto, 200 bolinhas
em cada saco):
•
POPULAÇÃO 1 - 100 bolinhas pretas representando o alelo A e 100 bolinhas brancas
representando o alelo B. Neste caso, portanto, teremos uma população onde os dois alelos têm
a mesma frequência [f(A) = f(B) = 0,5].
•
POPULAÇÃO 2 - 160 bolinhas pretas representando o alelo A e 40 bolinhas brancas
representando o alelo B. Neste caso, portanto, teremos uma população onde o alelo A tem
frequência de 80% e, o alelo B, frequência de 20% [f(A) = 0,8 e f(B) = 0,2].
•
POPULAÇÃO 3 - 40 bolinhas pretas representando o alelo A e 160 bolinhas brancas
representando o alelo B. Neste caso, portanto, teremos uma população onde o alelo A tem
frequência de 20% e, o alelo B, frequência de 80% [f(A) = 0,2 e f(B) = 0,8].
É importante que cada um dos sacos opacos seja identificado como uma das 3
populações definidas.
100
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
ROTEIRO DE ATIVIDADES
Após organizar as populações em seus respectivos saquinhos, propõe-se um roteiro de
atividades como o que se segue.
Jogo do Teorema de Hardy-Weinberg
Hardy e Weinberg mostraram (HARDY, 1908; WEINBERG, 1908) que as frequências
alélicas e genotípicas de uma população mantêm-se constantes ao longo das gerações,
independente de quão raros ou frequentes sejam os alelos em questão. Este modelo pressupõe
que:
1.
O tamanho da população seja infinito ou efetivamente infinito (ausência de deriva
genética);
2.
Que os cruzamentos aconteçam ao acaso (panmixia);
3.
Não haja diferença na taxa de reposição dos alelos (ausência de seleção natural), e;
4.
Que não haja a entrada de novas cópias dos alelos na população por meio de qualquer
fonte externa (ausência de migração ou modificações na estrutura dos alelos por força da
mutação).
O jogo
O jogo é composto por três populações de um lócus com dois alelos (A e B) e com três
frequências genotípicas diferentes entre si. Os alelos são representados por bolinhas de duas
cores distintas. Portanto, em cada saquinho são encontrados 200 alelos (bolinhas) e 100
indivíduos (pares de bolinhas) com proporções genotípicas assumidas como em equilíbrio de
Hardy-Weinberg, o que significa que as freqüências genotípicas em cada uma das populações
são respectivamente:
•
POPULAÇÃO 1 - Genótipos: 25 AA - 50AB - 25 BB, [f(A) = f(B) = 0,5].
•
POPULAÇÃO 2 - Genótipos: 64 AA - 32 AB - 04 BB, [f(A) = 0,8 e f(B) = 0,2].
•
POPULAÇÃO 3 - Genótipos: 04 AA - 32 AB - 64 BB, [f(A) = 0,2 e f(B) = 0,8].
As regras
Para fundar a F1 de cada população deve-se retirar, ao acaso, uma bolinha por vez,
anotar o alelo que ela representa e devolvê-la para o saco. A cada duas bolinhas sorteadas,
tem-se o genótipo de um indivíduo, que deve ser anotado a parte. Proceder desta forma até
101
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
obter uma amostra (prole - F1) com um total de 40 indivíduos para cada população (ou seja,
serão sorteadas, ao todo, 80 bolinhas para cada população).
Responda as questões
1.
Quais são as frequências alélicas da F1 de cada uma das três populações?
2.
Comparando os valores de frequência obtidos na F1 com aqueles da geração parental,
o que você observa?
3.
Teste a hipótese do equilíbrio de Hardy-Weinberg para a F1 de cada uma das três
populações usando a seguinte fórmula:
Ç2 = • [(o-e)²/e], onde:
“o” = valores genotípicos observados
“e” = valores genotípicos esperados.
A frequência genotípica esperada é obtida usando o binômio: p2+2pq+q2, onde:
“p” = frequência do alelo A [f(A) da F1]
“q” = frequência do alelo B [f(B) da F1]
Graus de liberdade: GL = número de fenótipos - número de alelos
A Tabela I apresenta a distribuição de valores qui-quadrado e suas probabilidades até cinco
graus de liberdade.
4.
Como você explica os resultados presentes na questão anterior?
Tabela I- Distribuição de qui-quadrado
G.L./P
1
2
3
4
5
0,9
0,016
0,211
0,584
1,064
1,61
0,8
0,064
0,446
1,005
1,649
2,343
0,7
0,148
0,713
1,424
2,195
3
0,5
0,455
1,386
2,366
3,357
4,351
0,3
1,074
2,408
3,665
4,878
6,064
0,2
1,642
3,219
4,642
5,989
7,289
0,1
2,706
4,605
6,251
7,779
9,236
0,05
3,841
5,991
7,815
9,488
11,07
0,01
6,635
9,21
11,345
13,27
15,08
102
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
APLICANDO A ATIVIDADE
Este jogo deve ser aplicado como prática de uma aula teórica na qual os conteúdos
referentes ao equilíbrio de Hardy-Weinberg tenham sido desenvolvidos (pressupostos, graus
de liberdade, qui-quadrado, trinômio do quadrado perfeito etc.). Desta forma, o objetivo desta
atividade é fazer que os alunos apliquem os seus conhecimentos sobre a hipótese de equilíbrio
de Hardy-Weinberg em uma situação prática. Portanto, espera-se, no momento da prática, a
operacionalização de conceitos. Assim, mais do que memorizar uma definição e seus
pressupostos ou resolver exercícios teóricos, o jogo aproxima o aluno da situação modelo de
reprodução sexuada em populações naturais. Este é um momento adequado (um segundo
momento, já que o primeiro foi a aula teórica) para que dúvidas e dificuldades sejam
evidenciadas e trabalhadas. O professor pode, ainda, exemplificar, de forma concreta, o que já
foi discutido em aula e os alunos têm a oportunidade de testar a hipótese de equilíbrio de
Hardy-Weinberg numa situação modelo.
RESPOSTAS ESPERADAS
A seguir são apresentadas respostas esperadas para cada uma das quatro questões
propostas. Os resultados numéricos são exemplos concretos obtidos de relatórios respondidos
por alunos que realizaram a prática.
1.
Quais são as frequências alélicas da F1 de cada uma das 3 populações?
Resposta esperada
Exemplo 1
Genótipos
AA
AB
BB
População 1
10
22
08
Exemplo 2
Genótipos
AA
AB
BB
População 1
08
19
13
População 2
17
21
02
População 2
26
12
02
População 3
01
09
30
População 3
02
10
28
Para calcular as frequências alélicas a partir das frequências genotípicas, é necessária a
fórmula: f(A) = [(2xHo)+He]/2xN, onde:
Ho = número de genótipos homozigotos
103
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
He = número de genótipos heterozigotos
N = tamanho da população
Assim, para o Exemplo 1, temos:
População 1: f(A) = [(2.10) + 22]/80 = 0,52 e f(B) = [(2.8) + 22]/80 = 0,48
População 2: f(A) = [(17.2) + 21]/80 = 0,69 e f(B) = [(2.2) + 21]/80 = 0,31
População 3: f(A) = [(2.1) + 9]/80 = 0,14 e f(B) = [(2.30) + 9]/80 = 0,86
No Exemplo 2, temos:
População 1: f(A) = [(2.8) + 19]/80 = 0,43 e f(B) = [(2.13) + 19]/80 = 0,57
População 2: f(A) = [(2.26) + 12]/80 = 0,80 e f(B) = [(2.2) + 12]/80 = 0,20
População 3: f(A) = [(2.2) + 14]/80 = 0,175 e f(B) = [(2.28) + 14]/80 = 0,825
2.
Compare os valores de frequência obtidos com os da população parental. O que você
observa?
Resposta esperada: Existe uma diferença entre as frequências genotípicas e gênicas da F1 e
da geração parental.
3.
Teste a hipótese do equilíbrio de Hardy-Weinberg para a F1 de cada uma das
populações.
Resposta esperada
Para solucionar esta questão é preciso, primeiramente, obter os valores de frequência
genotípica esperada para cada genótipo de cada população. Para que o valor obtido seja
relativo a toda a amostra da população, deve-se multiplicar cada valor do binômio pelo
tamanho da população (no caso, 40 indivíduos).
Exemplo 1
População 1
População 2
População 3
p² = (0,52)².40 = 10,816
q² = (0,48)².40 = 9,216
2pq = 2.(0,48).(0,52).40 = 19,968
p² = (0,69)².40 = 19,044
q² = (0,31)².40 = 3,844
2pq = 2.(0,69).(0,31).40 = 17,112
p² = (0,14)².40 = 0,784
q² = (0,86)².40 = 29,584
2pq = 2.(0,14).(0,86).40 = 9,632
População 1
População 2
População 3
p² = (0,43)².40 = 7,396
q² = (0,57)².40 = 12,996
p² = (0,80)².40 = 25,6
q² = (0,20)².40 = 1,6
p² = (0,175)².40 = 1,225
q² = (0,825)².40 = 27,225
Exemplo 2
104
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
2pq = 2.(0,43).(0,57).40 = 19,608
V Enebio e II Erebio Regional 1
2pq = 2.(0,80).(0,20).40 = 12,8
2pq = 2.(0,175).(0,825).40 = 11,55
Conhecendo as frequências genotípicas esperadas, é preciso compará-las com aquelas
observadas, obtendo o valor de qui-quadrado, que nada mais é do que um somatório do
módulo do valor do desvio de cada uma das classes genotípicas estandardizado pela
frequência genotípica esperada naquela classe. O valor do qui-quadrado nos oferece, portanto,
uma medida do desvio entre as frequências genotípicas observadas e as esperadas
teoricamente para a próxima geração. No Exemplo 1 temos:
População 1
AA
AB
BB
Ç2
Observado (o)
10
22
8
Esperado (e)
10,816
19,968
9,216
o-e
-0,816
2,032
-1,216
(o-e)²
0,66586
4,12902
1,47866
(o-e)²/e
0,06156
0,20678
0,1604
0,4287
População 2
AA
AB
BB
Ç2
Observado (o)
17
21
2
Esperado (e)
19,044
17,112
3,844
o-e
-2,044
3,888
-1,844
(o-e)²
4,17793
15,1165
3,4003
(o-e)²/e
0,21938
0,88339
0,88458
1,9873
População 3
AA
AB
BB
Ç2
Observado (o)
1
9
30
Esperado (e)
0,784
9,632
29,584
o-e
0,216
-0,632
0,416
(o-e)²
0,04666
0,39942
0,17306
(o-e)²/e
0,05951
0,04147
0,00585
0,1068
No Exemplo 2, temos:
População 1
AA
Observado (o)
8
Esperado (e)
7,396
o-e
0,604
(o-e)²
0,3648
(o-e)²/e
0,0493
AB
BB
19
13
19,608
12,996
-0,608
0,004
0,3697
0,000016
0,0188
≅0
Ç2
População 2
AA
AB
BB
Observado (o)
26
12
2
Esperado (e)
25,6
12,8
1,6
o-e
0,4
-0,8
0,4
(o-e)²
0,16
0,64
0,16
0,5125
Ç2
População 3
AA
AB
BB
0,0681
(o-e)²/e
0,00625
0,5
0,00625
Observado (o)
2
10
28
Esperado (e)
1,225
11,55
27,225
o-e
0,775
-1,155
0,775
(o-e)²
0,6006
1,3340
0,6006
Ç2
(o-e)²/e
0,4903
0,1155
0,4903
1,0961
Obtidos os valores de qui-quadrado é preciso, ainda, calcular os graus de liberdade. Os
graus de liberdade equivalem ao número de classes genotípicas esperadas que são
105
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
estatisticamente independentes. Aqui é importante chamar a atenção para o fato de que os três
casos em questão têm apenas um grau de liberdade, apesar de existirem três classes esperadas.
É que para o cálculo das classes esperadas são necessárias duas informações, isto é, o
tamanho da amostra e a freqüência de um dos alelos. Sabendo-se que o número de graus de
liberdade do qui-quadrado é igual ao número de classes esperadas menos o número necessário
de informações da amostra para o cálculo das proporções nessas classes, tem-se, neste caso,
que esse número é igual a um, pois 3 - 2 = 1, ou seja, GL = número de fenótipos - número de
alelos. Feito isto, é possível, com o auxilio da tabela oferecida, verificar que, para os
exemplos descritos, as chances de se encontrar desvios do tamanho daqueles obtidos para as
populações artificiais são:
No Exemplo 1:
População 1 (Ç2 = 0,4287), chance de ocorrência do desvio está entre 50-70%.
População 2 (Ç2 = 1,9873) chance de ocorrência do desvio está entre 10-20%.
População 3 (Ç2 = 0,1068) chance de ocorrência do desvio está entre 70-80%.
No Exemplo 2:
População 1 (Ç2 = 0,0681), chance de ocorrência do desvio está entre 70-80%.
População 2 (Ç2 = 0,5125) chance de ocorrência do desvio está entre 30-50%
População 3 (Ç2 = 1,0961) chance de ocorrência do desvio está entre 20-30%.
4.
Como você explica os resultados presentes na questão anterior?
Resposta esperada: não é possível rejeitar a hipótese de equilíbrio de Hardy-Weinberg para
nenhum dos casos estudados, uma vez que a chance de se encontrar desvios como os obtidos
apenas por acaso é muito alta (Mínimo de 10%, Máximo de 80%) e acima do nível de
significância estatística utilizado de 5%.
AVALIAÇÃO DA PRÁTICA
Esta atividade é aplicada regularmente em aulas práticas da disciplina “Evolução” do
curso de Ciências Biológicas da Universidade Federal Fluminense. As turmas desta disciplina
contam em média com 50 alunos e ao seu final os estudantes respondem um questionário de
avaliação da disciplina que contém perguntas sobre todas as práticas, incluindo o jogo sobre o
106
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
Teorema de Hardy-Weinberg. A Tabela II apresenta resultados da avaliação que este jogo tem
recebido por estes alunos.
Tabela II- Avaliação do Jogo do Teorema de Hardy-Weinberg realizada por alunos do curso
de graduação em Ciências Biológicas da Universidade Federal Fluminense (8 turmas = 278
alunos).
Sim
Parcialmente
Não
Pergunta/Resposta
Você gostou do jogo?
83,4%
8,5%
8,1%
Você acredita ter aprendido com o jogo?
95,6%
0%
4,4%
Você acha que o jogo deve continuar na disciplina?
94,7%
X
5,3%
Na Figura 1 é apresentada a variação semestral da aceitação do Jogo do Teorema de
Hardy-Weinberg pelos dos alunos.
Figura 1- Variação semestral da aceitação do Jogo do Teorema de Hardy-Weinberg por
alunos do curso de graduação em Ciências Biológicas da Universidade Federal Fluminense (8
turmas = 278 alunos).
Os resultados destas avaliações demonstram que o jogo vem obtendo boa aceitação
por parte dos alunos, indicando que esta atividade pode ser uma boa alternativa para todos
aqueles professores que encontram dificuldade em trabalhar com a teoria evolutiva,
especialmente no que se refere ao ensino do Teorema de Hardy-Weinberg (TIDON;
107
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
LEWONTIN, 2004). Mais que isso, o contato com os alunos durante o desenvolvimento da
atividade permitiu observar duas particularidades. Primeiro, o jogo tem o mérito de esclarecer
o significado do Teorema de Hardy-Weinberg. Por exemplo, noção de que o teorema
representa um esperado teórico, que as frequências gênicas de uma determinada população
permanecem constantes ao longo das gerações e que se está testando uma hipótese. A segunda
particularidade é evidenciar dúvidas pontuais. Por exemplo, os alunos enfrentam dificuldades
em entender as probabilidades apresentadas na tabela de qui-quadrado. Baseados nisso, outras
atividades têm sido desenvolvidas com o intuito de solucionar problemas que apresentam
certa regularidade. Por exemplo, jogos com moedas nos quais os alunos podem praticar e
entender melhor conceitos relacionados à frequência de desvios.
Espera-se que esta apresentação do Jogo do Teorema de Hardy-Weinberg, bem como
dos resultados positivos que ele vem alcançando, desperte o interesse de professores para
reproduzir esta atividade em suas aulas de genética e evolução e, também, promova a reflexão
sobre novas estratégias, alternativas e caminhos para o ensino da teoria evolutiva.
REFERÊNCIAS BIBLIOGRÁFICAS
DOBZHANSKY, T; LEVENE, H. Genetics of natural populations XVII.: Proof of operation
of natural selection in wild populations of Drosophila pseudoobscura. Genetics, Maryland, v.
33, n. 6, p. 537-547, 1948.
FUTUYMA, D.J. Biologia Evolutiva. Ribeirão Preto: FUNPEC Editora, 2009. 830 p.
GRIFFITH, A. J. F.; MAYER-SMITHIES, J. Understanding Genetics: Strategies for
Teachers and Learners in Universities and High Schools. New York: WH Freeman and
Company, 2000. 164 p.
HARDY, G. H. Mendelian Proportions in a Mixed Population. Science, Washington, v. 28, n.
708, p. 49-50, 1908.
KERR W. E.; WRIGHT; S. Experimental studies of the distribution of gene frequencies in
very small populations of Drosophila melanogaster: I. Forked. Evolution, New Jersey, v. 8, n.
2, p. 172-177, 1954.
KRASILCHIK, M. Prática de Ensino de Biologia. São Paulo: EdUSP, 2008. 197 p.
MERTENS, T. R. Introducing students to population genetics & the Hardy-Weinberg
principle. The American Biology Teacher, Virginia, v. 54, n. 2, p. 103-107, 1992.
SENE, F. M. O Teorema de Hardy-Weinberg completa 100 anos. Genética na Escola,
Ribeirão Preto, v. 3, n. 2, p. 39-41, 2008.
108
SBEnBio - Associação Brasileira de Ensino de Biologia
Revista da SBEnBio - Número 7 - Outubro de 2014
V Enebio e II Erebio Regional 1
TIDON, R; LEWONTIN, R. C. Teaching Evolutionary Biology. Genetics and Molecular
Biology, Ribeirão Preto, v. 1, n. 27, p. 124-131, 2004.
WEINBERG, W. Über den Nachweis der Vererbung beim Menschen. Jahresh. Ver. väter.
Naturk. Württemb. n. 64, p. 369-382, 1908.
109
SBEnBio - Associação Brasileira de Ensino de Biologia