Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
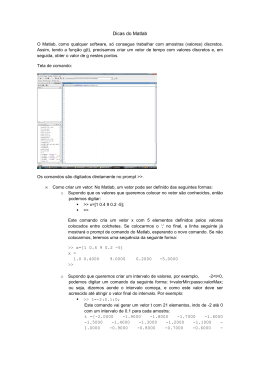
MATLAB
1) Introdução
O aplicativo Matlab é uma das ferramentas mais úteis para as áreas de processamento de
sinais, controle, e outras aplicações. O “Mat” do nome Matlab está relacionado com “Matriz”, ou
seja, é um laboratório que permite a manipulação eficiente de matrizes. Pode-se dizer também que o
Matlab permite também a manipulação eficiente de vetores, já que um vetor de tamanho N pode ser
visto como uma matriz de Nx1.
Uma das melhores formas de se familiarizar com o Matlab é através do comando intro, que
provê uma turnê pelas características básicas do programa.
Exercício 1
Use o comando intro e, com atenção, procure entender todos os exemplos fornecidos.
A aplicação predominante no presente curso será o processamento digital se sinais. Para
isto, preparamos algumas técnicas em Matlab que facilitarão o uso do aplicativo para esta tarefa.
2) Geração de Sinais Amostrados
Como primeiro exemplo, geraremos a seguinte função senoidal no Matlab:
f(t)=sin(2*pi*fo*t)
Onde fo=1 Hz.
A função é mostrada na seguinte figura:
Senoide de 1 Hz
1
0.8
0.6
0.4
0.2
f(t)
0
-0.2
-0.4
-0.6
-0.8
-1
0
0.2
0.4
0.6
Tempo (seg.)
0.8
1
1
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
Para permitir o processamento de sinais por computador, o sinal analógico deve ser
digitalizado por um conversor analógico para digital (A/D). Neste processo o sinal é amostrado em
vários instantes, em intervalos de tempo constante. O intervalo de tempo é o período de amostragem
(T), e o recíproco de T é a freqüência de amostragem (fs= 1/T). A unidade de tempo do período de
amostragem em geral é segundos, e a de Freqüência é em Hz. 100 Hz significa que 100 amostras do
sinal são tomadas em 1 segundo.
Pode-se simular funções amostradas no Matlab. O exemplo abaixo mostra como se pode
simular a amostragem de uma senóide no Matlab:
Exercício 2
Siga os passos descritos para simular a amostragem de uma onda senoidal no seguinte
exemplo. Digite os comandos na Matlab, e observe os efeitos.
1) Crie o eixo do tempo:
t=0:0.05:1;
O comando acima cria uma variável (vetor) com os elementos 0, 0.05, 0.1, ..., 1. O ponto e
vírgula evita que a variável seja exibida na tela. Tente rodar o comando acima e observe o que
acontece. Caso você tenha errado, e o vetor inteiro comece a aparecer na tela, você pode parar o
processo usando CTRL-C.
O comando size(t) exibe o tamanho da matriz t, e o comando length(t) mostrará o comprimento do
vetor. Experimente estes comandos.
2) Crie a função:
f=sin(2*pi*t);
O comando acima cria um vetor cujas componentes são a função senoidal calculada a cada valor do
vetor t. Assim, no Matlab, você pode calcular o seno de um vetor, ou mesmo de uma matriz.
Execute este comando.
3) Plotar a função:
plot(t,f)
Este comando faz a plotagem do sinal, tendo f no eixo y, e o correspondente t no eixo x.
Execute este comando.
4) Coloque o Titulo e as variáveis dos eixos x e y:
title(‘Funcao Senoidal’)
xlabel(‘Tempo (segundos)’)
ylabel(‘Amplitude (Volts)’)
2
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
Experimente os comandos acima.
Tente também os seguintes comandos:
plot(f,t)
plot(f)
plot(t)
O que aconteceu no primeiro comando? No segundo comando, a senóide foi plotada, mas o
eixo y mostrou simplesmente o número da amostra, mas não o tempo correspondente a cada abcissa
y. Explique o que acontece no terceiro exemplo.
Tente também as seguintes opções:
plot(t,f,’*’)
plot(t,f,’b*’)
plot(t,f,’.’)
plot(t,f,’c.’)
plot(t,f,’-’)
plot(t,f,’y-’)
Observe as cores e características dos gráficos. Agora digite help plot, e leia
cuidadosamente as descrições da função plot.
Agora digite a seguinte função:
grid
Note o efeito da função, e digite help grid, para ver as características desta função.
Agora gere uma segunda função:
f2=sin(2*pi*2*t)
E plote as funções f e f2 no mesmo gráfico:
plot(t,f,t,f2)
Verifique as cores dos gráficos. Agora digite:
plot(t,f,’b*’,t,f2,’c-.’)
E verifique os efeitos.
Agora tente os seguintes comandos:
stem(t,f)
stem(t,f2)
3
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
O que estes comandos fazem? Digite help stem, e estude o funcionamento desta função.
Tente mudar as cores dos traçados desta função. Note que a função não é tão flexível quanto a cores
do traçado quanto a função plot.
3) Geração de sinais mais complexos
Digite os seguintes vetores:
A=[0 1 2 3 4 5 6];
B=[0 2 4 6 8 10 12];
Tente multiplicar A*B. Note que o Matlab não realizará tal operação. O fato é que o Matlab
sempre interpretará o vetor como uma matriz, e o programa sempre interpreta uma multiplicação
como uma multiplicação de matrizes. Entretanto, há uma opção que permite ao usuário fazer uma
multiplicação ponto a ponto de dois vetores ou matrizes (isto é o primeiro elemento do resultado é o
produto dos primeiros elementos dos fatores, o segundo elemento do resultado é o produto dos
segundos elementos dos fatores, e assim por diante). Tente digitar:
C=A.*B
Note que o vetor C é o resultado da multiplicação ponto a ponto do dos vetores A e B.
Exercício 3
Queremos plotar a seguinte função no intervalo 0<x<4:
y(x)=(x-1)(x-2)
Para isto, criamos primeiro o vetor representando a variável x, e em seguida a função em
questão:
x=0:0.05:4;
y=(x-1).*(x-2);
plot(x,y)
Note o comando “.*”. Cada expressão entre parênteses é um novo vetor, e os vetores são
multiplicados ponto a ponto, resultando no efeito desejado.
Agora geraremos a função:
y(x)=x3-6x2+11x-6
4
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
Para isto, criamos primeiro o vetor representando a variável x, e em seguida a função em
questão:
x=0:0.05:4;
y=x.^3-6*x.^2+11*x-6;
plot(x,y)
Note que o operador “.^” é também um operador ponto a ponto, que eleve cada elemento da
matriz à potência desejada. Tente digitar x^2, e veja que este comando não funcionará. Tente
descobrir porque (lembre-se que o Matlab sempre assume operações matriciais).
PROBLEMAS
1) Gere e plot a função f(t)=exp(-t)sin(2*5*pi*t), no intervalo 0<x<6. Use várias escolhas de
intervalo para o eixo x: 0.1 sec., 0.05 sec., etc., e escolha o que tem melhor aparência.
2) Ache graficamente as raízes da função y=x3+2x2-x+1. (Dica: procure, por tentativa e erro o
intervalo, a o período de amostragem do eixo x, realizando sucessivas plotagens das tentativas).
3) Plote a seguinte função: y=sin(x)*cos(2x)/(2+sin(x)). Escolha um eixo x apropriado (Não se esqueça
que as multiplicações e divisões devem ser operações ponto a ponto).
4) Gere a função f(t)=sin(2*pi*10*t), no intervalo 0<x<10. Qual é a freqüência desta senóide? Use
as seguintes escolhas de freqüência de amostragem: 5 Hz, 10 Hz, 20 Hz, 40 Hz, e 200 Hz. Use a
função stem. Observe bem o efeito, pois será analisado na próxima aula.
5) Gere a função f(t)=exp(-t)sin(2*5*pi*t), e depois plote um histograma da mesma. Dica: use a
função intro, e observe o uso da função bar. Em seguida digite help bar, para analisar aquela
função.
5
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
EXERCÍCIOS COM O MATLAB
Nesta seção, veremos algumas funções extras do Matlab. Primeiramente, consideremos o
seguinte trecho a seguir. Analise atentamente o programa abaixo (consulte o help para as funções
que você não conhece):
% exemplo: geracão de uma forma de onda ruidosa
t=0:0.01:pi;
%linha 1
y=2*sin(5*t);
%linha 2
figure(GCF)
%linha 3
plot(t,y)
%linha 4
pause
%linha 5
ruido=randn(1,length(t)); %linha 6
plot(t,ruido)
%linha 7
pause
%linha 8
y_ruido=y+ruido;
%linha 9
plot(t,y_ruido);
%linha 10
Execute o programa. A linha 1 cria o vetor do tempo de amostragem. A linha 2 cria uma
função senoidal (qual é a freqüência?). A linha três faz com que a janela com o gráfico seja
colocada à frente de todas as outras. A linha 4 plota uma senóide, como mostrado abaixo:
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
0.5
1
1.5
2
2.5
3
3.5
O comando pause, na linha 5, causa uma pausa no programa. Para continuar o programa, o
usuário deve pressionar <Enter>. [Pergunta: o que acontece se este comando for substituído por
pause(2)? Dica: use o comando help].
A linha 6 utiliza o comando randn (utilize o help para aprender sobre este comando). Este
comando gera uma seqüência de números aleatórios com distribuição normal, com uma linha e
tantas colunas quanto for o comprimento do vetor t. O comando lenght(t) fornece o número de
elementos de t. Observe a plotagem do sinal de ruído:
6
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
3
2
1
0
-1
-2
-3
0
0.5
1
1.5
2
2.5
3
3.5
Em seguida, a linha 9 calcula uma nova variável y_noise, que é o sinal senoidal mais o
ruído. Observe o resultado:
4
3
2
1
0
-1
-2
-3
-4
-5
0
0.5
1
1.5
2
2.5
3
3.5
Neste exemplo, você aprendeu como gerar um sinal com ruído.
Agora, vejamos outros comandos. Para isto considere o seguinte código:
% Exemplo 2
A=[1 2 3; 4 5 6]
B=[3 4 ; 3 6 ; 7 8]
C=[1 2 3 ; 4 5 6 ; 7 8 9];
D=[5 6 ; 7 8 ; 9 10];
pause
size(A)
size(B)
pause
7
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
length(A)
length(B)
Após executar o código acima, realize manualmente, e em seguida usando o Matlab, as
seguintes operações (indique quando a operação não é possível):
A*B=
B*A=
A*C=
A^2=
A.^2=
C^2=
C.^2=
A’=
C*inv(C)=
[B B B]=
[A;A;A]
Veremos agora alguns comandos estatísticos. Considere o seguinte trecho de código:
% exemplo 3
A=[ 1 2 3 4 5 6 7]
%linha 1
B=mean(A)
%linha 2
C=std(A)
%linha 3
Pause
%linha 4
RUIDOSO=randn(1,5000); %linha 5
figure(gcf)
%linha 6
plot(RUIDOSO)
%linha 7
title('sinal ruidoso') %linha 8
pause
%linha 9
MEDIA_RUIDOSO=mean(RUIDOSO)
%linha 10
DP_RUIDOSO=std(RUIDOSO) %linha 11
Pause
%linha 12
MAISRUIDO=5*randn(1,5000);
%linha 13
MEDIA=mean(MAISRUIDO)
%linha 14
DP=std(MAISRUIDO)
%linha 15
8
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
Use o comando help para estudar os comandos mean, e std. Execute o programa. Tome
cuidado de só incluir o ponto-e-vírgula quando necessário. Estes comandos calculam a média e o
desvio padrão dos vetores em questão (relembre na literatura o que estes termos significam). Na
linha 2, o resultado, B, será a média dos elementos do vetor A Na linha 3, o resultado C será o
desvio padrão dos elementos do vetor A. Calcule A e B manualmente, e cheque os resultados com
os resultados do Matlab.
Na linha 5 um sinal de ruído normal é gerado, e é plotado na linha 6. A média e o desvio
padrão são calculados e mostrados nas linhas 10 e 11. Note que a função randn gera ruído aleatório
com média 0, e desvio padrão 1 (na verdade, próximos de 0 e 1). Para obter um ruído com maior
intensidade (maior desvio padrão), basta multiplicar o ruído pelo desvio padrão desejado, como é
feito nas linhas 13, 14 e 15. Analise com cuidado estas três últimas linhas.
EXERCÍCIOS
1) Usando o comando help, aprenda a lidar com os comandos max, min, mean, median, sort.
2) Usando o comando help, aprenda a usar os comandos fix, floor, ceil, round, mod,
rem, sign.
3) Gere uma senóide com freqüência de 50 Hz e amplitude 3V, amostrada a uma freqüência de
amostragem de 1 kHz. Adicione a esta senóide ruído gaussiano com desvio padrão de 2V. Plote
o sinal resultante. Determine os valores máximo e mínimo deste sinal. Não se esqueça de incluir
título e unidades. Procure plotar o sinal de forma que suas características fiquem claras ao leitor
(deve ficar claro que o sinal é uma senóide com ruído).
4) Usando o comando help square, aprenda como gerar uma onda quadrada. Gere uma onda
quadrada de 10 Hz, amostrada a uma freqüência de 1 KHz.
9
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
REVISÃO: NÚMEROS COMPLEXOS
1) Representação dos Números Complexos
Números complexos são uma estrutura criada como uma extensão dos números reais. À
primeira vista, esta estrutura parece ser artificial e inútil. Entretanto, na prática suas aplicações são
inúmeras. Este capítulo apresentará uma revisão resumida do tópico, devida à sua importância nas
séries de Fourier.
Um número complexo é um par ordenado de números reais (R,I), e é muito usualmente
representado na seguinte forma:
C=R+iI, ou C=R+jI
Sendo que matemáticos preferem o uso do i, enquanto os engenheiros preferem o j. R é
chamado parte real, e I é chamado parte imaginária do número complexo. Note que se I é zero, o
número se transforma em puramente complexo, e se R é zero, o número é puramente imaginário.
Os números complexos seguem certas regras algébricas, que a princípio parecem estranhas,
mas que permitem a extensão de várias técnicas matemáticas, bem como possibilitam um grande
números de aplicações. É muito comum se representar os números complexos em um plano
ordenado x,y, da forma ilustrada na Figura 1.
imaginario
(x,y)
M cos(α)
M
a=tan-1(y/x)
X=M sin(α)
Real
Figura 1 - Representação gráfica de um número complexo
O módulo ou magnitude M de um número complexo é representado geometricamente pela
reta ligando a origem à coordenado do par ordenado, e é definido como:
M=sqrt(x2+y2)
O ângulo ou fase α, do número complexo é o ângulo entre a reta mencionada e o eixo x, e é
definido como:
α=tan-1(I/R)
É fácil mostrar, observando a geometria da Figura 1 que:
10
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
R=M cos(α)
I=M sin(α)
Muitas vezes o número complexo é representado por seu módulo e sua fase, da seguinte
maneira:
M∠α
Exercício 1:
Considere os seguintes números:
A=1+j2
B=-2+j3
C=4-j1
D=-2-j2
1) Plote manualmente cada um do números, e enumere em que quadrante o número está (1o., 2o.,
3o., ou 4o.) e depois plote os mesmo usando o Matlab (plot(A) plota o número complexo, caso o
mesmo realmente seja complexo).
2) Para cada número, calcule manualmente o módulo M, e depois faça os cálculos com o Matlab
(comando abs(A)). Confira os resultados com os cálculos manuais.
3) Calcule manualmente os ângulos α (atente para os quadrantes) e em seguida repita os cálculos
em Matlab (comando atan(x/y)). Tente também a função atan2(x/y), e observe que a mesma
leva em consideração o quadrante em que o número está.
4) A partir dos valores de M e α calculados, determine x e y. Faça o mesmo em Matlab (Exemplo,
x=M*cos(alfa), y=M*sin(alfa)).
5) Digite A=1+j2, e em seguida, digite:
real(A)
imag(A)
O que acontece? Qual é a função dos comandos acima?1
6) Digite o seguinte código:
A=[ 1+j*2 ; 2+j*3 ; 4-j*1 ; 2-j*2 ]
plot(A)
M=abs(A)
grid
alfa1=atan(real(A)./imag(A))
11
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
alfa2=atan2(real(A),imag(A))
Areal=M.*cos(alfa2)
Aimag=M.*sin(alfa2)
Tente entender todos os comandos. Note que os exercícios de 1 a 4 foram implementados
nesta linha. Note o caráter matricial (ou vetorial) das variáveis (preste atenção nos pontos do .*, e ./
.
6) Converta os seguintes números para a forma R+jI:
2 π/3
3 60o
4 π/2
2) Álgebra dos Números Complexos
Os números complexos são sujeitos a regras de álgebra, algumas delas semelhantes à
álgebra dos números reais, e algumas diferentes. Quando os números complexos são puramente
reais, a álgebra simplesmente se transforma na álgebra dos números reais.
Suponha os números complexos A e B:
A=Ar+ j Ai
B=Br+ j Bi
Estes números complexos são sujeitos às seguintes regras:
Soma:
A+B=(Ar + Br) + j ( Ai + Bi)
Valor de j:
j=i=sqrt(-1)
Quadrado de i:
i2=-1
Multiplicação:
A . B=( Ar+ j Ai).( Br+ j Bi)= Ar Br +j Ai Br+j BrAi+j2AiBi
= (ArBr - AiBi)+j (ArBi+AiBr)
Raiz n-ésima (fórmula de de Moivre):
1/n
A =
n
a+2kp
|A| ∠ n
Complexo conjugado de R+jI :
R-jI
Multiplicação de um número complexo por seu conjugado:
(A+jB)(A-jB)=A2+B2
(note a eliminação da parte complexa)
12
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
Eliminação de partes complexas no denominador:
A+jB = A+jB C-jD = (AC-BD) + j(AD-BC)
C+jD C+jD C-jD
C2+D2
Exercício 2
Suponha:
M= 1+j2
N= 3+j4
Calcule primeiro manualmente, e depois em Matlab. Dê os resultados na forma R+jI :
1) M+N
2) MN
3) M/N
4) M2
5) sqrt(M)
6) M1/3
7) M1/5
8) Determine todas as raízes cúbicas de 8 (Fórmula de de Moivre ou Matlab)
9) Eleve todas as raízes encontradas em na questão 8 ao cubo.
3) Fórmula de Euler:
Duas fórmulas fazem os números complexos muito úteis:
ejω = cos ω + j sin ω
e-jω = cos ω - j sin ω
Ou equivalentemente:
cos ω = ejω + e-jω
2
jω
sin ω = e − e-jω
j2
Note que
cos ω = Re (ejω)
sin ω = Im (ejω)
13
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
Exercício 3
1) Defina uma variável de tempo com 0<t<5, amostrada em intervalos de 0.01 segundos, e calcule a
função
f(t)=e2jπt
Usando seus conhecimentos, tente prever o comportamento desta função. Note que a função
é formada por uma parte real senoidal, e uma parte imaginária cossenoidal. Plote a parte real e a
parte imaginária na Função no Matlab:
ParteReal=real(f);
ParteImag=imag(f);
subplot(2,1,1)
plot(t,ParteReal)
subplot(2,1,2)
plot(t,ParteImag)
2) A função também pode ser dividida em uma parte função módulo e fase. Tente prever a forma
das funções módulo e fase da função seus conhecimentos. Use o Matlab para plotar estas
funções:
Módulo=abs(f);
Fase=atan2(imag(f),real(f));
subplot(2,1,1)
plot(t,Módulo)
subplot(2,1,2)
plot(t,Fase)
3) Multiplique a função complexa f, calculada no exercício anterior, pelo número complexo 1+j1, e
chame a nova função de f2. Plote as partes reais de f1 e f2 no mesmo gráfico. Observe o efeito da
multiplicação por um número complexo. Por que este efeito ocorre? Preste bastante atenção a
esta questão, pois é central para o entendimento posterior dos conceitos de resposta em
freqüência, e FFT.
4) Gere a função f(t)=sin(2πt). Multiplique esta função por 1+j1, gerando f2. Plote no mesmo
gráfico as partes imaginárias de f e f2. Note os efeitos, e explique-os.
A FFT e a DFT
O Matlab permite o cálculo fácil da DFT e da FFT. Se tivermos um vetor A, de n elementos,
a DFT do mesmo é:
14
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
FFTdeA=fft(A);
E para a FFT inversa, é usada a seguinte forma:
IFFTdeA=ifft(FFTdeA);
Caso o número de elementos de A seja da forma 2k, o Matlab usa o algoritmo da FFT (mais
rápido). Caso contrário, é usado o algoritmo da DFT. Considere o seguinte exemplo:
t=(0:.01:.99);
f=sin(2*pi*2*t);
F=fft(f);
subplot(2,1,1)
plot(abs(F),'ko')
subplot(2,1,2)
plot(angle(F),'ko')
O resultado é mostrado a seguir:
50
40
30
20
10
0
0
10
20
30
40
50
60
70
80
90
100
0
10
20
30
40
50
60
70
80
90
100
4
2
0
-2
-4
Note que foram plotados o ângulo e a fase da FFT. Isto porque o resultado é um vetor com
números complexos. Tente plotar o vetor sem a função abs. Explique a razão para o resultado
aparentemente absurdo.
Neste exemplo, é calculada a DFT de 1 segundo de amostragem de uma senóide com 2 Hz.
15
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
Note que o resultado da fase foi estranho. A razão é que a fase é o resultado de divisões de
números muito pequenos por números muito pequenos, resultando num valor não significativo.
Substitua agora a primeira linha por
t=(0:.01:1.3);
e execute o programa. O resultado é mostrado a seguir:
50
40
30
20
10
0
0
20
40
60
80
100
120
140
0
20
40
60
80
100
120
140
4
2
0
-2
-4
Nota-se que neste último caso ocorreu o fenômeno do “leakage”. Este fenômeno não
ocorreu no primeiro caso porque as amostras completavam um ciclo completo (a menos de uma
amostra). Para que não ocorra leakage, é necessário que esta precaução seja tomada.
Voltemos agora ao primeiro exemplo. Nota-se que o eixo dos x não corresponde ã
freqüência e sim ao número da amostra. Para que seja mostrada a amostra, é necessário que a
mesma seja calculada. Para tal, suponhamos que a freqüência de amostragem seja fs e que o sinal
contenha N amostras. Neste caso, a primeira amostra corresponderia à freqüência zero, e a amostra
N (que não existe, já que as amostras vão de 0 a N-1) corresponderia à freqüência de amostragem.
Assim, a freqüência de cada amostra, na DFT resultante corresponderia a fs/N. Por exemplo, a
16
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
primeira amostra corresponderia à freqüência zero, a Segunda a fsN, a terceira a 2fs/N, e a n-ésima a
(n-1)fs/N.
Outra observação importante é com respeito à amplitude. A amplitude da senóide no
exemplo é de 1 V, e a amplitude da DFT foi de 50. Isto se deve ao fato de que o resultado da
FFT é sempre multiplicado pelo número de amostras. Assim, para se Ter uma estimativa
confiável das componentes espectrais, é necessário que se divida o resultado por N.
Tendo essas considerações em mente, execute o seguinte código:
clear
% Limpa variáveis
clf
% Limpa gráficos
t=(0:.01:.99);
% Gera instantes das amostras
fs=100;
% Freqüência de amostragem
N=length(t);
% Determina o número de amostras
f=1+sin(2*pi*10*t);% Amostra o sinal formado por
% uma cte + senóide
F=fft(f);
% Calcula a DFT
Fesc=F/N;
% Escalona para o valor correto
freq=(0:N-1)*fs/N; % Calcula eixo das freqüências
plot(freq,abs(Fesc),’ko’)
% Plota o módulo da DFT
xlabel(‘Freqüência ’)
% Label do eixo x
ylabel(‘Amplitude’)
% Label do eixo y
O resultado é mostrado a seguir:
17
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
1.4
1.2
Amplitude
1
0.8
0.6
0.4
0.2
0
0
10
20
30
40
50
60
Freqüência
70
80
90
100
FILTROS DIGITAIS
O Matlab apresenta muitas funções que facilitam a implementação de filtros digitais.
Observe o help da função filter.
FILTER One-dimensional digital filter.
Y = FILTER(B,A,X) filters the data in vector X with the
filter described by vectors A and B to create the filtered
data Y. The filter is a "Direct Form II Transposed"
implementation of the standard difference equation:
a(1)*y(n) = b(1)*x(n) + b(2)*x(n-1) + ... + b(nb+1)*x(n-nb)
- a(2)*y(n-1) - ... - a(na+1)*y(n-na)
If a(1) is not equal to 1, FILTER normalizes the filter
coefficients by a(1).
When X is a matrix, FILTER operates on the columns of X. When X
18
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
is an N-D array, FILTER operates along the first non-singleton
dimension.
[Y,Zf] = FILTER(B,A,X,Zi) gives access to initial and final
conditions, Zi and Zf, of the delays. Zi is a vector of length
MAX(LENGTH(A),LENGTH(B))-1 or an array of such vectors, one for
each column of X.
FILTER(B,A,X,[],DIM) or FILTER(B,A,X,Zi,DIM) operates along the
dimension DIM.
See also FILTER2, FILTFILT (in the Signal Processing Toolbox).
Assim, a função tem, em geral, três argumentos: os vetores A e B, correspondentes aos
coeficientes dos filtros, e o vetor de entrada. O resultado da função é o vetor de saída.
Antes de fazermos um exemplo com a função filter, vamos observar que o Matlab possui
várias ferramentas que permitem a determinação dos coeficientes A e B. Um exemplo é a função
butter. Observe o help desta função:
BUTTER Butterworth digital and analog filter design.
[B,A] = BUTTER(N,Wn) designs an N'th order lowpass digital
Butterworth filter and returns the filter coefficients in length
N+1 vectors B and A. The cut-off frequency Wn must be
0.0 < Wn < 1.0, with 1.0 corresponding to half the sample rate.
If Wn is a two-element vector, Wn = [W1 W2], BUTTER returns an
order 2N bandpass filter with passband W1 < W < W2.
[B,A] = BUTTER(N,Wn,'high') designs a highpass filter.
[B,A] = BUTTER(N,Wn,'stop') is a bandstop filter if Wn = [W1 W2].
When used with three left-hand arguments, as in
[Z,P,K] = BUTTER(...), the zeros and poles are returned in
length N column vectors Z and P, and the gain in scalar K.
When used with four left-hand arguments, as in
[A,B,C,D] = BUTTER(...), state-space matrices are returned.
BUTTER(N,Wn,'s'), BUTTER(N,Wn,'high','s') and BUTTER(N,Wn,'stop','s')
design analog Butterworth filters. In this case, Wn can be bigger
than 1.0.
See also BUTTORD, BESSELF, CHEBY1, CHEBY2, ELLIP, FREQZ, FILTER.
19
Tópicos em Processamento de Sinais
Departamento de Engenharia Elétrica
Faculdade de Tecnologia
Universidade de Brasília
Vê-se que esta função determina os coeficientes de um filtro de Butterworth de ordem n, com uma
freqüência de corte fc. A freqüência de corte é indicada de forma que o valor 1 corresponda à
metade da freqüência de amostragem fs. Por exemplo, se fs=100Hz, 0.1 corresponderia a uma
freqüência de corte de 5 Hz.
Como exemplo, será filtrada uma senóide de 15 Hz, amostrada a 100 Hz, por um filtro com
fc=10 Hz.
clear
clf
t=(0:.01:1);
f=sin(2*pi*5*t);
% amostragem do sinal
subplot(2,1,1)
plot(t,f)
% Sinal de entrada
ª
[B,A]=butter(1,0.1); % Calcula coeficientes do filtro de 2 ordem,
% fs/2=50Hz e fo=5Hz, entao Wn=5/50=0.1
saida=filter(B,A,f); % Filtra o sinal. Resultando no vetor de
% saída.
subplot(2,1,2)
plot(t,saida)
Execute este código, e explique o resultado.
EXERCÍCIOS
1) Gerar um sinal f(x)=1+sin(2100t), amostrado a 1KHz.
2) Passar o sinal por um filtro passa-baixas Butterworth com fc=50 Hz.
3) Passar o sinal por um filtro passa-baixas Butterworth com fc=50 Hz.
4) O Matlab possui a função freqz, que permite plotar a resposta em freqüência de filtros digitais.
Examine o help desta função, e use-a para plotar a resposta em freqüência do filtro do último
exemplo.
20