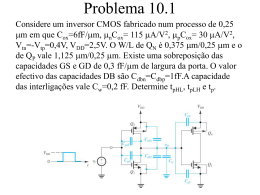
1) Conceitos fundamentais de circuitos lógicos
O principal elemento de um circuito lógico é o inversor. O
inversor está para circuitos digital como o amplificador esta para
circuitos analógicos.
Vários conceitos fundamentais serão apresentados algumas vezes
faremos uso do inversor para explica-los. São estes:
•
•
•
•
•
Margem de ruído;
Atraso de propagação;
Dissipação de potência;
Produto atraso-potência;
Fan-in Fan-out;
Margem de ruído
Considere uma característica de transferência de tensão de um
inversor qualquer, como mostrado na figura 1.1. Para simplificar
utilizamos três retas para aproximar a função de transferência que
normalmente é uma função linear da entrada.
Como mostra a figura se a entrada for alta (vi > vIH ) a saída será
igual a v0L. E, se a entrada for baixa (vi > vIL ) a saída será igual a v0H.
Note que o nível alto de saída não depende do valor exata da tensão de
entrada desde que esta não exceda vL. Quando o inversor (porta) excede
esta tensão este entra na região chamada região de transição. Da
mesma forma o nível lógico não depende do valor exato da tensão de
entrada desde que esta não seja menor do que vIL. As tensão vIH, vIL, v0L
e v0H são importantes na característica de transferência do inversor.
A margem de ruído expressa a insensibilidade da porta lógica na
presença de ruído.
VI
V0
Figura 1.1 O Inversor lógico
V0
V0H
V0L
VIL
VIH
Figura 1.2 Característica de transferência
VI
Quanto maior a insensibilidade da saída de uma porta
lógica a presença de ruído maior sua margem de ruído. Para
quantificar esta insensibilidade considere o circuito mostrado
na figura 1.3. Uma situação muito comum em que a saída de
uma porta esta conectada a entrada de uma outra.
RUÍDO
VI =VIO
V0 = V0H
V0 =V0L
Figura 1.3 Cascata de dois inversores.
Se a saída do primeiro inversor estiver em nível alto com
valor v0H notamos que existe uma margem de segurança no
segundo inversor igual a diferença entre v0H e vIH (veja a figura
1.4) que garante uma saída deste em nível lógico baixo (v0L).
Em outra palavras se por alguma razão sinal indesejado
(chamado ruído) é superposto ao da saída do primeiro inversor,
a saída do inversor subseqüente não será afetada enquanto o
ruído não reduzir a tensão em sua entrada a valores menores
que vIH. Portanto podemos dizer que o inversor possui uma
margem de ruído para nível alto, MRH, de
MRH = V0H - VIH
(1.1)
V0
V0H
MRL
MRH
V0L
VIL
VIH
V0H
VI
Figura 1.4 Margem de Ruido
De modo semelhante, se a saída do primeiro inversor
estiver em nível baixo com valor V0L, o segundo inversor
produzirá uma saída em nível alto mesmo que o ruído altere o
nível lógico V0L em sua entrada, elevando-o até próximo de V0L.
Logo podemos afirmar que o inversor possui uma margem de
ruído para nível alto, MRL, de
MRL = VIL – V0L
(1.2)
Resumindo;
Parâmetro Importantes
V0L : Nível baixo de saída
V0H : Nível alto de saída
VIL : Valor máximo de entrada (ainda interpretado como
nível lógico 0)
V0H : Valor mínimo de entrada (ainda interpretado como
nível lógico 1)
MRL : Margem de ruído para nível baixo = VIL – V0L
MRH : Margem de ruído para nível alto = V0H – VIH
• Os valores VIL, V0L, V0L e V0H da característica de
transferência definem a margem de ruído da porta
lógica.
• As alterações no nível de tensão de entrada, dentro
da margem de ruído da porta são rejeitados por
esta.
Questão: Se V0H = VIH = VDD = 5,0V e se VIL = V0L = 0V,
qual a máxima margem de ruído? Desenhe a curva
característica. Esta seria uma curva ideal?
2) Atraso de propagação
Nos amplificadores lineares o comportamento dinâmico
dos amplificadores é especificado em termos de sua resposta
em freqüência, já em circuitos lógico o comportamentos
dinâmico é caracterizado pelos tempos de atraso temporal entre
o chaveamento lógico dos níveis alto para baixo e vice-versa e
a respectiva mudança na saída. Tal atraso, chamado atraso na
propagação, é devido a duas razões:
1) Os transistores que implementam as chaves exibem
tempos de chaveamento finitos;
2) Uma capacitância que inevitavelmente está presente
nas saída e entrada das portas lógica.
Antes de continuarmos faremos uma breve revisão dos
circuitos com constante de tempos simples (CTS).
Circuitos com constantes de tempos simples são aqueles
compostos, de ou que podem ser reduzidos a, um dos
componentes reativos (indutância ou capacitância) e uma
resistência.
Para redução dos circuitos mais complexos utilizamos
algum processo, tais como
Teorema de Thévenin
Teorema de Norton
Princípio da superposição.
A regra é muito simples e consiste em encontrar a
resistência vista pelos terminais da capacitância ou indutância.
Faremos alguma exercícios para demonstração.
1) Exemplo 1: Qual a constante de tempo do circuito abaixo?
R1
B
ve
C
R2
Thévenin
2) Exemplo 2: Idem anterior
R1
R3
ve
R2
C
R4
Thévenin
3) Exemplo 3: Idem anterior
ve
C1
C
R
Thévenin
4) Exemplo 4: Idem anterior
R2
ve1
C1
R1
ve2
C
Thévenin
C2
5) Exemplo 5: Idem anterior
ie
C
R
Thévenin
6) Exemplo 6: Idem anterior
R2
ie
R1
C
Thévenin
Em todas as configurações: τ = RC
Considere uma entrada do tipo degrau aplicada a um
circuito CTS (passa-baixas) com constante de tempo τ. A saída
para qualquer tempo t é dada por
V0(t) = V∞ - (V∞ -V0)exp(-t/τ)
(1.3)
Onde V∞ é o valor final, isto é, o valor para qual a saída tende
para um tempo infinito, e V0 é o valor da resposta em t= 0.
Exercício 1.1:
Considere o inversor da figura abaixo com um capacitor
C=10pF conectado entre a saída e o terra. Sejam VDD = 5V, R=
1 kΩ, RON = 100 Ω e VOffset = 0,1V. Se, para t = 0, VI torna-se
baixo e, negligenciando o tempo de atraso da chave, ou seja,
supondo que ela abre imediatamente, determine o tempo para
que a saída atinja ½(VOH + VOL). O tempo para esse ponto de
transição 50% da forma de onda é definido como atraso na
propagação de nível baixo para nível alto (low-to-high
propagation delay, tPLH).
Solução:
Em primeiro lugar, determinamos V0L , da figura
temos
V0L = Voffset + (VDD – Voffset)/(R+RON)* RON
= 0,1 + (5 -0,1)/(1,1)* 0,1 = 0,55V
A seguir, o capacitor carrega-se por meio de R e v0 aumenta
exponencialmente em direção a VDD. A forma de onda esta
mostrada na figura e sua equação é
v0 = 5 – (5 – 0,55)exp(-t/τ)
em que τ = RC.
Para calcular tPLH, substituímos V0L
O resultado é
tPLH = 0,69 τ = 6,9ns
Concluindo nos mostramos na figura 1.5 a definição forma
do atraso na propagação de um inversor. Como mostrado, um
pulso com tempos de subida e descida finitos (diferentes de
zero) é aplicado a entrada. O pulso de saída invertido exibe
tempos de subida e descida finitos (chamados de tTLH e tTHL, em
que o índice T denota transição, e LH denota de “baixo para alto”
e HL denota de “alto para baixo”.
Arquivos para simulação em www.sedrasmith.org