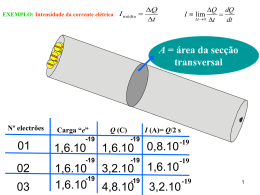
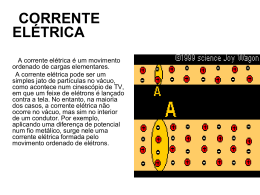
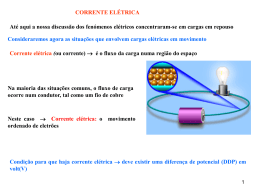
Exemplo: Velocidade de Migração num Fio de Cobre
As velocidades de migração típicas nos
condutores são muito pequenas. De facto a
velocidade de migração é muito menor que a
velocidade média entre colisões. Para a
velocidade obtida no problema acima, os
electrões levariam 68 minutos para deslocarse 1m.
Então por que uma luz quando ligada acende instantaneamente? O campo eléctrico que impulsiona os electrões
livres é estabelecido no condutor instantaneamente. Quando ligamos o interruptor a força eléctrica faz com que
os electrões passem a se deslocar no fio, imediatamente. Os electrões que já se encontravam no filamento da
lâmpada passam a se deslocar em resposta a essa força, e a lâmpada começa a emissor luz.
1
Exemplo: INTENSIDADE DA CORRENTE ELÉTRICA  I
A = área da secção
transversal
Nº electrões
01
Carga “e”
-19
1,6.10
-19
02
03
Q (C)
I (A)= Q/2 s
-19
1,6.10
-19
0,8.10
-19
-19
1,6.10 3,2.10 1,6.10
-19
-19
1,6.10 4,8.10 3,2.10 -19
2
RESISTÊNCIA
Vd  está relacionada com o campo eléctrico, E no fio

E

se E aumentar, a Fe sobre os electrões é mais forte e vd aumenta
V  E
I  V
assim
Podemos escrever essa proporcionalidade como
V = IR

I
A constante de proporcionalidade R é chamada de
resistência do condutor
I
V
Esta resistência é causada por colisões dos electrões
com os átomos do condutor
R
V
I
Unidade SI: volt/ ampère, chamada de ohm ()
RESISTÊNCIA 
3
Resistência à passagem da corrente eléctrica no fio
R
4
LEI DE OHM
Verificou-se experimentalmente que para muitos materiais, incluindo os metais, a resistência é
constante para grande parte das tensões aplicadas.
Esse comportamento é conhecido como lei de Ohm 
(1787-1854)
em homenagem a Georg Simon Ohm
 foi a primeira pessoa a fazer um estudo sistemático da resistência eléctrica.
A lei de Ohm não é uma lei fundamental da natureza, mas uma relação empírica válida somente
para determinados materiais e dispositivos, sob uma escala limitada de condições
V  IR
V
I
R
O declive é
m
1
R
(a)
(b)
a) Curva da corrente em função da tensão para um dispositivo óhmico. A curva é linear e o declive
2 103
1
1
fornece a resistência do condutor :
3
m
2
 10
R
m

103
 1000
b) Uma curva não linear da corrente em função da tensão para um díodo semicondutor.
Esse dispositivo não obedece à lei de Ohm.
5
O símbolo para um resistor em diagramas de circuito
A resistência de um fio condutor óhmico é proporcional ao seu comprimento e inversamente
proporcional à sua área de secção transversal:
R

A
  resistividade do material
Unidades da resistividade : ohm-metro ( )

 comprimento do fio
Condutividade 
 
1

 tem a unidade (  m )-1

R

A
6
Exemplo: Um condutor de alumínio tem 300m de comprimento e 2mm de diâmetro. Calcule a sua
resistência eléctrica.
Dados: Comprimento do fio, L=300m, diâmetro do fio, D=2mm, resistividade do alumínio
2.810-8 .
Solução
R=1mm
A=R2 =3.14(1mm)2 =3.14 mm2 =3.1410-6 m2
Considerando a resistividade expressa em (Ohmm). Nesse caso o comprimento deve estar expresso
em m, e a área da secção em m2, portanto substituindo na expressão da resistência resulta:
 2.8 108  300
R 
 2.67 
6
A
3.1410
7
VARIAÇÃO DA RESISTIVIDADE COM A TEMPERATURA
A resistividade depende de vários factores, um dos quais é a temperatura
É de se esperar, uma vez que com o aumento da temperatura os
rapidamente
átomos movem-se mais
 no aumento de colisões entre os electrões livres e os átomos
   0 1   T  T0 
Fio frio
Fio quente
T0  20  temperatura de referência
  o coeficiente de temperatura
da resistividade
como

R
A
 R

R  R0 1   T  T0 
RESISTIVIDADE EM TERMOS DE PARÂMETROS MICROSCÓPICOS

me
ne2
  tempo médio entre as colisões
8
SUPERCONDUTORES
Para uma classe de metais e de compostos conhecidos como supercondutores, a resistência vai a
zero abaixo de uma determinada temperatura crítica Tc
As resistividades dos supercondutores abaixo de Tc são
menores do que
4  10-25   m
Alumínio, Estanho, chumbo
1017 vezes menor do que a resistividade do cobre e
considerada como nula na prática.
Uma das características
verdadeiramente
notáveis
dos supercondutores é o
facto que, uma vez que uma
corrente é criada neles, ela
persiste (por anos) sem
nenhuma tensão aplicada
(porque R = 0):
A segunda característica denominada de Efeito Messner: é o
diamagnetismo perfeito, ou seja, exclusão do campo magnético de
seu interior.
Um imã levitando sôbre o nitrogénio líquido refrigerado à
temperatura de -200  C. 
9