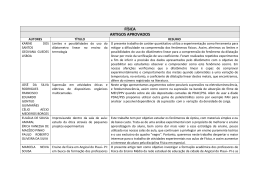
Universidade Federal da Integração Latino-Americana
Fundação Parque Tecnológico Itaipu
Curso de Especialização em Energias Renováveis
Ênfase em Biogás
______________________________________________________________
DISCIPLINA: Fontes de Energia e suas Aplicações
PROFESSORES: Carlos Alberto dos Santos, Janine Padilha Botton e Pedro
Henrique Konzen
COMPLEMENTO: Tópicos de Matemática
Neste módulo, vamos identificar áreas da matemática que são necessárias no desenvolvimento de teorias e tecnologias relacionadas a fontes de energias e suas transformações. Não é nosso objetivo neste módulo, apresentar de forma plena as diversas disciplinas
de matemática aqui correlacionadas, mas sim, de desenvolvermos alguns exemplos práticos onde estas disciplinas são de fundamental inportância.
Unidade 4.1 - A matemática, fontes de energia e suas transformações
Alguns de nós poderiam estar se perguntando: o que a matemática tem haver com
fontes de energia e suas transformações? Para respondermos esta pergunta, devemos observar que a matemática se desenvolve, não somente, em um âmbito disciplinar, mas também
através das relações multi- e interdisciplinares com as diversas ciências da natureza, como
física e química.
É comum a observação de que teorias matemáticas são ferramentas utilizadas na
física, química, biologia, economia, etc.. Isto não está de todo errado, se entendemos que
as ferramentas devem ser desenvolvidas e/ou adaptadas para um dado trabalho. Além disso, essa observação não esclarece um fato importante. Quando nos apoiamos em teorias
matemáticas (ou seja, quando utilizamos matemática), estamos tomando por hipótese que o
fenômeno estudado segue a lógica matemática. Ou seja, no estudo das ciências da natureza,
e aqui engloba os estudos sobre fontes de energia e suas transformações, a matemática não
é somente uma linguagem (como muitos confundem), mas sim, uma afirmação (uma hipótese) de que os fenômenos estudados podem ser entendidos através de proposições lógicas.
Podemos notar que a matemática apoia o desenvolvimento de teorias e tecnologias relacionadas a fontes de energia e suas transformações, bem como, muitos outros estudos relacionados as ciências da natureza, observando os seguintes pontos:
–
a “linguagem” utilizada é precisa e concisa;
–
existe um rico conjunto de teoremas matemáticos para serem explorados,
utilizados e desenvolvidos;
–
a exigência de estabelecer hipóteses explícitas, ajuda a diminuir a adoção de
suposições implícitas e, por consequência, clarifica as restrições de cada teoria;
–
permite a análise de muitas variáveis de forma integrada.
Por exemplo, no módulo 1, seção 1.3 “Princípio da Conservação de Energia”,
exemplificamos a conservação de energia mecânica através do estudo de um objeto de
massa
m , abandonado em seu estado de repouso a uma altura
h da superfície. Ali,
utilizou-se de equações matemáticas, afim de esclarecer algumas partes da discussão de
forma precisa e concisa.
Agora, ao escrevermos as equações matemáticas (ou seja, ao modelar matematicamente), assumiu-se uma série de hipóteses intrínsecas da teoria matemática aplicada. Por
exemplo, na Equação (1.5), o trabalho é definido pela expressão
2
W =∫ F⋅dr
(4.1)
1
ou seja, o trabalho é dado pela integral do ponto 1 ao ponto 2 do produto interno da força
resultante pelo diferencial do deslocamento. Agora, para que possamos utilizar a teoria do
cálculo para calcularmos o trabalho
W , o deslocamento do ponto 1 ao ponto 2 deve se-
guir uma trajetória contínua por partes e a força
F também deve ser uma função contí2
nua por partes. Estas são restrições impostas ao problema que se deseje estudar. Isto é, não
é uma restrição da teoria da conservação de energia, mas uma limitação de aplicação da teoria matemática escolhida.
Agora, o que ocorre, por exemplo, quando temos garantido que todas as hipóteses
físicas e matemáticas necessárias são cumpridas, mas da modelagem matemática obtemos
um resultado que não é fisicamente possível? Bem, neste caso, diríamos que o modelo (ou
a teoria física) assumido está, no mínimo, incompleto. Ou seja, assume-se, em geral, que o
fenômeno não está colocando em cheque a lógica matemática, mas sim, que ainda não
compreendemos ele completamente. Aqui, a teoria matemática não é apenas uma linguagem, mas uma hipótese (quase uma certeza).
Dito isso, devemos reforçar que um bom domínio de algumas áreas da matemática
é indispensável para o desenvolvimento de tecnologia para a produção de energia. Por
exemplo, o desenvolvimento de um biodigestor necessitará, no mínimo, o domínio de Matemática Básica, Cálculo Diferencial e Integral, Cálculo Vetorial, Álgebra Linear, Equações Diferenciais e Cálculo Numérico. Estas são todas disciplinas de base na formação de
engenheiros.
Unidade 4.2 - Matemática Básica
Aqui, entendemos por matemática básica as teorias de lógica matemática, de conjuntos, relações e funções, álgebra elementar, trigonometria, geometria plana e espacial,
noções de geometria analítica, entre outras. Estas teorias, além de serem indispensáveis
para todas as áreas da matemática são, ainda, ferramentas usuais do dia a dia (quem nunca
necessita fazer um cálculo de vez em quando?).
Neste tema, existe uma vasta bibliografia disponível para consulta. Livros de ensino fundamental e médio são, normalmente, bastante pedagógicos, por exemplo, BONJORNO, 2010. Uma referência completa é a coleção Fundamentos de Matemática Elementar.
Ainda, para consultas pontuais, recomendamos os compêndios de matemática, por exem-
3
plo: SPIEGEL, 2004; BRONSHTEIN, 2007.
Como exemplo de aplicação de matemática básica, voltemos ao módulo 1, seção
1.3 “Princípio da Conservação de Energia”. Quando utilizamos a segunda Lei de Newton,
concluímos que
P=mg
ou seja, o peso
P é igual a massa
(4.2)
m vezes a aceleração da gravidade
g . Isto defi-
ne o peso como uma função da massa e da gravidade, isto é:
P m , g =mg
Esta é uma função polinomial em
m e
(4.3)
g . Notamos ainda, que é uma função
linear em uma das variáveis, se deixarmos a outra constante. Em fim, podemos explorar
uma gama enorme de teorias matemáticas elementares para estudarmos as implicações desta equação. Para exemplificarmos, suponhamos que queiramos, neste caso, determinar as
condições suficientes para que o peso seja zero. Neste caso, é fácil inferir que a massa deve
ser zero ou a aceleração da gravidade deve ser nula. Entretanto, não existe objeto de massa
zero, como também, a aceleração da gravidade (que esta relacionada a força gravitacional)
pode ser zero. Assim, mesmo que matematicamente a função peso tenha infinitos zeros
(qualquer ponto
m , g =0, g  ou
m , g =m , 0 é raiz da função peso) , fisicamen-
te, isso nunca ocorrerá.
Podemos, ainda, identificar outros exemplos práticos, como na construção de um
biodigestor. É comum o tanque de um biodigestor ter a forma de um paralelepípedo. Neste
caso, o volume de biomassa suportado pelo tanque pode ser facilmente calculado com base
na teoria de geometria espacial. Aqui, o volume do tanque é dado por
V =abc
onde,
a ,
b e
(4.4)
c são os comprimentos das arestas do paralelepípedo. Assim, pode-
mos definir as dimensões do tanque com base na quantidade de biomassa que será demandada.
Estes são apenas dois exemplos em que teorias de matemática básica aparecem naturalmente. Podemos identificar inúmeros outros exemplos. Como veremos a seguir, a ma4
temática básica é, ainda, fundamental para compreendermos teorias mais complexas, como
as de Cálculo Diferencial e Integral.
Unidade 5.3 - Cálculo Diferencial e Integral
O Cálculo Diferencial é uma poderosa ferramenta para estudarmos variações de
quantidades (por exemplo, velocidade, aceleração, taxa de reação, taxa de crescimento,
etc.) . Não é nosso objetivo, aqui, de ter um curso de Cálculo, mas, sim, de desenvolver alguns exemplos práticos onde o Cálculo é de grande ajuda no desenvolvimento de tecnologias para a produção de energia.
Para interessados em aprofundar, ou iniciar, seus estudos em Cálculo, recomendamos STEWART, 2010. Existem, ainda, muitas outras referências nessa direção como, por
exemplo: LEITHOLD, 1994; ANTON, 2005; entre outros. Ainda, para consultas pontuais,
recomendamos os compêndios de matemática, por exemplo: SPIEGEL, 2004;
BRONSHTEIN, 2007.
Vamos, agora, a alguns exemplos de práticos. No módulo 1, seção 1.4.1 “Varáveis
de Estado”, vimos a Lei dos Gases Ideais, a qual estabelece:
PV =nRT
(4.5)
onde, P é a pressão em Pascal que o gás está submetido, V é o volume de gás em metros cúbicos, n é a massa do gás em moles, R é a constante universal dos gases (
R=8,314 J / mol⋅K  ) e
T é a temperatura em Kelvin. Esta equação, define a tempe-
ratura como uma função da pressão, do volume (supondo n constante), isto é:
T  P ,V =
PV
nR
(4.6)
Agora, suponhamos que queremos determinar de que maneira a variação da temperatura no tempo está relacionada a variação de pressão e volume no tempo. Para tanto, podemos utilizar a Regra da Cadeira, da qual obtemos:
5
∂T V ∂ P P ∂V
=

∂ t nR ∂ t nR ∂t
(4.7)
P
Ou seja, a variação de temperatura em um certo instante ( ∂T /∂t ) irá depender de
e
V neste instante como, também, da variação de pressão e volume neste instante. Da
Equação (4.7), podemos tirar várias conclusões. Por exemplo, imagine que temos um balão
cheio de um certo gás (vamos supor que este gás possa ser tratado como um gás ideal). Ao
pressionarmos o balão, aumentamos a pressão, mas o volume de gás permanece o mesmo.
Assim, pela Equação (4.7), sabemos que a temperatura do gás irá aumentar. Como, também, sabemos que ela irá aumentar proporcionalmente a pressão que estamos fazendo.
A teoria de Cálculo Integral também aparece frequentemente em diversas áreas relacionadas ao entendimento de fontes de energia e suas transformações. Seu potencial prático e teórico vem da relação entre derivadas e integrais. Esta relação é dada pelo Teorema
Fundamental do Cálculo, que estabelece:
b
∫ f  x  dx=F b− F  a
(4.8)
a
onde,
f  x =
dF
dx
(4.9)
Ou seja, a integral é a operação inversa da derivada e vice-versa.
Um exemplo de aplicação da integral foi dada no módulo 1, seção 1.4.2 “Calor”,
onde a equação (1.15, naquela seção):
T2
Q=m∫ c dT
(4.10)
T1
que estabelece que a quantidade de calor necessária para elevar a temperatura de um corpo
de massa
m , de um valor inicial
T 1 a um valor final
T 2 , é dada pelo produto da
massa do corpo e a integral da capacidade térmica por unidade de massa do corpo em relação a temperatura.
Estudos de cálculo é aplicado a funções que associam vetores a pontos no espaço,
6
são desenvolvidos em Cálculo Vetorial.
Unidade 4.4 - Cálculo Vetorial
No Cálculo Vetorial estudamos o cálculo de campos vetoriais, esses campos são
funções que associam vetores a pontos do espaço. As mesmas referências bibliográficas
apresentadas na seção anterior podem ser consultadas para aprofundar os estudos nesta
área.
Esta teoria é aplicada, por exemplo, na determinação do trabalho efetuado por um
campo de força agindo sobre um objeto que se move ao longo de uma curva, ou ainda, na
determinação da vazão de um fluído (gás, água, etc.) através de uma superfície. Devemos,
ainda, observar, que é uma extensão para várias dimensões da teoria de Cálculo Diferencial
e Integral unidimensional. Por exemplo, o Teorema Fundamental do Cálculo é estendido a
mais variáveis pelos conhecidos Teorema de Green, Teorema de Stokes e Teorema do Divergente.
Como exemplo da aplicação de Cálculo Vetorial, voltamos ao módulo 1, seção 1.3
“Princípios da Conservação de Energia”. Lá, vimos que um campo (gravitacional, eletromagnético, ou de outra natureza) realiza trabalho por meio da ação de sua força,
F , so-
bre o objeto. O trabalho para transportar o objeto de um ponto 1 para um ponto 2 é definido pela integral de linha:
2
W =∫ F⋅d r=∫ F⋅d r
C
onde,
(4.11)
1
C é a curva formada pelo movimento do objeto no espaço. A igualdade acima
afirma que a integral de linha depende somente da posição inicial e final do objeto. Isto é
verdade, desde que o campo de forças
F seja conservativo. Daí, podemos calcular esta
integral e obteremos:
1
1
W = m v 22 − v 1 2
2
2
onde,
v1
e
(4.12)
v 2 são as velocidades do objeto no ponto 1 e 2, respectivamente. Agora,
7
pela definição da energia cinética,
E c , temos
W = E c =E c  2−E c 1
(4.13)
ou seja, o o trabalho é a diferença entre a energia cinética no ponto 2 e a energia cinética
no ponto 1. Ainda, a energia potencial de um objeto está relacionada ao campo de forças
pela expressão
F=−∇ E v
(4.14)
W =∫ F⋅d r=−∫ ∇ P⋅d r
(4.15)
e, portanto, temos
C
C
Agora, calculando esta última integral, obtemos
W = P= P 2−P 1
(4.16)
ou seja, o trabalho é a diferença entre a energia potencial no ponto 2 e a energia potencial
no ponto 1.
Assim, das Equações (4.13) e (4.16), podemos concluir que
E c 1E v 1=E c 2E v 2
(4.17)
isto é, a soma da energia cinética e a energia potencial permanece constante. Essa é chamada Lei da Conservação de Energia.
Outra área da matemática de fundamental importância é a Álgebra Linear.
Unidade 4.5 - Álgebra Linear
A Álgebra Linear estuda espaços vetoriais lineares, os quais estão relacionados a
sistemas de equações lineares. Podemos observar, que as teorias desta área da matemática
são aplicadas tanto em nível prático como em nível teórico em várias ramificações da matemática. Do ponto de vista teórico, por exemplo, é uma disciplina fundamental para o estudo de Equações Diferenciais. Para aprofundar os estudos neste ramo da matemática, indicamos: STRANG, 1988; KOLMAN, 2005, entre outros.
8
b
c
R1=5Ω
I1
d
R3=10Ω
+ I2
- E2=100V
+ E1=40V
-
I3
+
E3=50V
R2=10Ω
R4=20Ω
a
e
f
Figura 4.1: Circuito Elétrico.
Vejamos um exemplo prático na análise de circuitos elétricos. Consideramos o circuito mostrado na Figura 4.1, formado por baterias, resistências e cabos. As baterias têm os
potenciais elétricos ( E i ) indicados, assim como, as resistências ( Ri ). O problema
que vamos desenvolver de forma resumida, é de determinar as correntes ( I i ) que fluem
por cada segmento do circuito. Temos três segmentos, como indica a figura. O segmento
f a  b , com corrente
to
I 1 , o segmento
c d e  f , com corrente
f  c , com corrente
I 2 , e o segmen-
I 3 . As direções das correntes foram arbitrariamente
escolhidas.
Pela Lei da Corrente de Kirchhoff, a soma das correntes de entrada é igual a soma
das correntes de saída, nos pontos c
e
f , portanto:
I 3=I 1 I 2
no ponto
c e, obtemos a mesma equação no ponto
(4.18)
f . Assim, como as equações são
linearmente dependentes, só precisamos de uma delas. Agora, ao aplicarmos a Lei de Voltagem de Kirchhoff em cada ciclo, obteremos o seguinte sistema de equações lineares:
E 1−R1 I 1 −E 2R 2 I 2=0
(4.19)
−R3 I 3E 3− R4 I 3− R2 I 2 E 2=0
(4.20)
E 1−R1 I 1 −R3 I 3E 3 −R4 I 3=0
(4.21)
Agora, substituindo os valores indicados na Figura 4.1 e escrevendo este sistema de
9
equações lineares na sua forma algébrica, obtemos:
[
][ ] [ ]
1 1 −1 I
0
1
−5 10 0
60
I =
0 −10 −30 2 −150
−5 0 −30 I 3
−90
(4.22)
Para resolver este sistema e encontrar os valores das correntes, podemos utilizar, por exemplo, o Método de Gauss-Jordan, mas isso foge de nosso objetivo neste curso. Um exemplo
similar, pode ser encontrado em KOLMAN, 2005.
De fato, é importante ressaltarmos que existem muitos teoremas importantes de Álgebra Linear que são fundamentais no desenvolvimento de tecnologias para a produção de
energia. Os teoremas de Espaços Vetoriais, por exemplo, são especialmente importantes no
estudo de Equações Diferenciais.
Unidade 4.6 - Equações Diferenciais
Equações diferenciais são equações matemáticas, nas quais um ou mais de seus termos são derivadas. O estudo de tais equações forma um vasto campo da matemática. Elas
são, particularmente, importantes na modelagem de complexos problemas. Para aprofundarmos os estudos de Equações Diferenciais, indicamos as referências: ZILL, 2003; BOYCE, 2001; entre outros.
Vamos nos concentrar num exemplo de grande importância para a geração de energia com biogás. O biogás é formado, basicamente, por metano ( CH 4 ), dióxido de carbono ( CO 2 ), nitrogênio ( N 2 ) e várias espécies químicas traço. Assim, o único combustível presente no biogás é o metano. A combustão do metano tem a seguinte equação
química global:
CH 42O2 7.524 N 2 CO 2 2 H 2 O7.524 N 2
(4.23)
Agora, do ponto de vista físico, a combustão é um problema de escoamento reativo
(veja, WARNATZ, 2001, para modelagem de problemas em combustão) . No nosso caso,
10
tem-se o escoamento dos gases metano, oxigênio, nitrogênio que reagem liberando calor e
formando dióxido de carbono e água (estado gasoso). De fato, esta equação global é apenas
um modelo simplificado do que realmente ocorre, mas ela serve para nosso objetivo aqui.
Da teoria de Dinâmica de Fluídos, podemos modelar matematicamente este problema através do seguinte sistema de equações diferenciais parciais:
∇⋅u u ,T , M =0
(4.24)
 u⋅∇ u−∇⋅ ∇ u∇ p=−0  g
(4.25)


 u⋅∇  i−∇⋅


∇ h =−∇⋅q R
cp
(4.26)
1

∇ xi =
ṙ , i=1, , nsp
Mc p
Mi i
(4.27)
 u⋅∇ h−∇⋅

nsp
onde, u denota o campo de velocidade, T a temperatura,
M =∑ x i M i a massa moi=1
lar média,  a massa específica,  o coeficiente da viscosidade, p a pressão hidroρ 0 massa específica do ar a temperatura ambiente
T =298 K,
dinâmica,
T
2
c
g=(0,0 ,−9.81) o vetor gravidade (m/s ), h a entalpia específica,
p capacidade
R

de calor total,
coeficiente de condutividade térmica, q é o fluxo de calor radioativo, M i massa molar, ṙ i taxa de reação da i-ésima espécie, i =wi / M i o número de
mole específico da i-ésima espécie, w i a fração de massa da i-ésima espécie e x i a fração molar da i-ésima espécie. O modelo é fechado com a equação de estado:
=
Pth M
RT
(4.28)
e pela aproximação de baixo número de Mach

=u⋅
onde,
1
1
∇ M− ∇ T
M
T

(4.29)
Pth é a pressão termodinâmica.
Nosso objetivo, aqui, não é de compreender o significado de cada uma destas equações, mas sim, observar que consiste em um sistema de equações diferenciais que descrevem (modelam) o fenômeno da combustão de gases. De fato, este sistema de equações é
tão complexo que até hoje não se conhece nenhuma solução exata para ele. Tão pouco se
sabe se este sistema de equações tem solução. Agora, é viável obtermos aproximações de
11
possíveis soluções (e, assim, obter informações de grande valia) através do emprego de
técnicas de Cálculo Numérico.
Unidade 4.7 - Cálculo Numérico
O Cálculo Numérico é uma área da matemática que lida, principalmente, com aproximações numéricas. A importância deste ramo da matemática tem ganhado importância
com o desenvolvimento dos computadores modernos, com enorme capacidade de processamento e capacidade de armazenamento de dados. Em aplicações práticas, o Cálculo Numérico, normalmente, é visto como um conjunto de técnicas numéricas (ferramentas computacionais) que auxiliam na obtenção de soluções aproximadas para problemas que não se
conhece solução exata ou que o processo de calcular a solução exata é demasiado custoso
(seja computacionalmente, seja por sua complexidade).
Aqui, dois textos são indicados para aqueles que queiram aprofundar seus estudos
no tema. BURDEN, 2003, apresenta uma abordagem didática de Cálculo Numérico. Já,
PRESS et al., 2007, apresenta o tema em uma abordagem computacional.
Na análise de processos de geração de energia, há vários exemplos de aplicações de
Cálculo Numérico. Essas aplicações vão desde simples interpolações e ajustes de curvas de
dados coletados (por exemplo, aproximação dos mínimos quadrados) até técnicas de alta
eficiência computacional para a solução de sistemas de equações diferenciais (simulação).
Este é o caso do sistema de equações diferenciais visto na seção anterior. Para buscarmos uma solução aproximada para ele, necessitamos de grande capacidade computacional, associada a técnicas numéricas avançadas como multigrid, refinamento de malha local
e adaptativo, modificações do método de Newton, apenas para citar algumas.
Vejamos uma aplicação mais simples. Suponhamos que o tanque de um biodigestor
tem o formato de um cocho (veja a Figura 4.2.) com 5m de comprimento e raio da seção
transversal de 1m. Suponhamos, ainda, que podemos calcular o volume de biomassa
V
12
contida no tanque pela seguinte equação:
V =5 [ 14,13−9 arcsenh /3−h9−h2  1/ 2 ]
(4.30)
onde, h é a altura do topo do tanque até a superfície de biomassa. Agora, vamos ao problema. Se vamos colocar V 0 metros cúbicos de biomassa no tanque, quanto vale h ?
Figura 4.2: Tanque (acima) e sua seção transversal (abaixo).
A Equação (4.30) define uma equação implícita para
h em função de
V0
e,
portanto, não podemos resolver este problema de forma algétrica. Agora, podemos utilizar
técnicas numéricas para obtermos uma solução aproximada com tolerância de erro pré-determinada. Para tanto, definimos a função
f h por:
f h=V 0−5 [ 14,13−9 arcsenh /3−h9−h2  1/ 2 ]
e, portanto, o problema é equivalente a determinar
h , tal que,
(4.31)
f h=0 . Pelo Método
da Bissecção, seguimos o seguinte algoritmo:
Passo 1: Determinamos h 1 e h 2 tais que
Passo 2: Tomamos
f h 2 0 ;
p=h1 h2 /2 ;
Passo 3: Se ∣ f  p∣TOL
Passo 4: Se
f h 10 e
vamos ao Passo 6, senão executamos os Passos 4 e 5;
f h 1 f  p0 , então tome
h 1= p . Caso contrário, tome
h 2= p .
Passo 5: Tomamos
p=h1 h2 / 2 e voltamos ao Passo 3;
Passo 6: Fim! O valor procurado é h= p .
13
Síntese do Módulo
Neste módulo discutimos, de forma bastante sucinta, alguns tópicos de matemática
que são fundamentais no entendimento e desenvolvimento de tecnologias para a geração de
energia. Ressaltamos as seguintes áreas da matemática:
–
Matemática Básica;
–
Cálculo Diferencial e Integral;
–
Cálculo Vetorial;
–
Álgebra Linear;
–
Equações Diferenciais;
–
Cálculo Numérico;
Bibliografia
ANTON, H.; BIVENS, I.; DAVIS, S.; Cálculo, vol. 1 e 2, 8ª ed., editora Bookman, 2005.
BONJORNO, J.R.; GIOVANNI, J.R.; GIOVANNI Jr., J.R.; Matemática – Uma nova
abordagem, vol. 1, 2 e 3, editora FTD, 2010.
BOYCE, W.E.; DIPRIMA, R.C.; Elementary Differential Equations and Boundary Value
Problems, 7ª ed., editora John Wiley & Sons, 2001.
BRONSHTEIN, I.N. et al.; Handbook of Mathematics, 5ª ed., editora Springer, 2007.
BURDEN; R.L.; FAIRES, J.D.; Análise Numérica, 7ª ed., editora Thompson, 2001.
Fundamentos de Matemática Elementar, vol. 1-10, 7ª ed., editora Atual, 2005.
KOLMAN, B; HILL, D.R.; Álgebra Linear, 8ª ed., editora Pearson, 2005.
LEITHOLD, L; O Cálculo com Geometria Analítica, vol. 1 e 2, 3ª ed., editora Harbra,
14
1994.
PRESS, W.H.; et al.; Numerical Recipes – The art of Scientific Computing, 3ª ed., editora Cambridge University Press, 2007.
SPIEGEL, M.R.; LIU, J.; Manual de Fórmulas e Tabelas Matemáticas, ed. 2ª, editora
Bookman, 2004.
STEWART, J; Cálculo, vol. 1 e 2, 2ª ed., editora Cengage Learning, 2010.
STRANG, G; Linear Algebra and its Aplications, 3ª ed., editora Thompson Learning,
1988.
ZILL, D.G.; Equações Diferenciais com Aplicações em Modelagem, editora Cengage
Learning, 2003.
WARNATZ, J.; MAAS, U.; DIBBLE, R.W.; Combustion: Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation, 3ª ed., editora Springer, 2001.
15