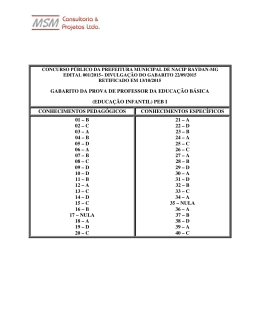
1) Um corpo, inicialmente em repouso,
está sendo deslocado por uma força de
direção e sentido constante e módulo
variável, conforme o diagrama abaixo.
O trabalho realizado por essa força ao
deslocar o corpo da posição 0 m à
posição 25 m é:
a) 600 J
b) 350 J
c) 300 J
d) 1.000 J
e) 650 J
Resp. A
RESOLUÇÃO
A área sob o gráfico F×d fornece o trabalho realizado pela força. Vamos subdividir essa área em
um retângulo e um triângulo. Depois somamos tudo.
retângulo: b  h  25 m  20 N = 500 J
b  h 10 m  20 N

 100 J
2
triângulo: 2
O trabalho total é 500 J + 100 J = 600 J
2) O corpo C, representado na figura a seguir, desloca-se na direção da força de módulo igual a
2,0 N. Durante um deslocamento de 1,0 m, qual é o
trabalho realizado pelas forças que atuam sobre o corpo?
(Considere desprezíveis os atritos.)
a) 1,0 J
b) 2,0 J
c)
5
2
J
d)
5 J
e)3,0 J
Resp: B
RESOLUÇÃO
d=1m
 = 0°
A força de 1 N, perpendicular ao deslocamento, não realiza trabalho. O trabalho é devido apenas
à força de 2 N.
  F.d.cos     2 N  1 m    2
J
3) A casa de Dona Maria fica no alto de uma ladeira. O desnível entre sua casa e a rua que passa
no pé da ladeira é de 20 metros. Dona Maria tem 60 kg e sobe a rua com velocidade constante.
Quando ela sobe a ladeira trazendo sacolas de compras, sua velocidade é menor. E seu coração,
quando ela chega à casa, está batendo mais rápido. Por esse motivo, quando as sacolas de
compras estão pesadas, Dona Maria sobe a ladeira em ziguezague. O fato de Dona Maria subir a
ladeira em ziguezague e com velocidade menor está diretamente associado à redução de:
O fato de Dona Maria subir a ladeira em ziguezague e com velocidade menor está diretamente
associado à redução de:
a) potência.
b) aceleração.
c) deslocamento.
d) energia.
e) trabalho.
Resp: A
RESOLUÇÃO
Ao subir em ziguezague, ela está usando o fato de que o trabalho da força peso depende apenas
da posição final e da posição inicial. Então ela realiza o mesmo trabalho num espaço de tempo
maior, o que faz com que a potência seja menor.
4) Para arrastar um corpo de 100 Kg de massa entre dois pontos com movimento uniforme, um
motor de potência igual a 500 W opera durante 120 s. O trabalho realizado pelo motor é
a) 3,0 × 104 J.
b) 6,0 × 104 J.
c) 1,0 × 104 J.
d) 2,0 × 104 J.
e) 4,0 × 104 J
Resp: b
RESOLUÇÃO
m = 100 Kg
P=
T
MRU
P = 500 W
J
 T = P.Δt = 500 ×120 s  P
Δt
s
t = 120 s
T=?
= 6×104 J
5) Um ciclista desce uma ladeira, com forte vento contrário ao movimento. Pedalando
vigorosamente, ele consegue manter a velocidade constante. Pode-se então afirmar que:
a) A energia cinética está aumentando.
b) A energia cinética está diminuindo.
c) A energia potencial gravitacional está aumentando.
d) A energia potencial gravitacional está diminuindo.
e) A energia potencial gravitacional é constante.
Resp.:D
RESOLUÇÃO
Ao descer ele perde energia potencial gravitacional, mas isso não é suficiente para manter sua
velocidade constante, por isso ele ainda dispende da própria energia do corpo para compensar o
forte vento contrário.
Conversão energia potencial em cinética + energia do corpo = energia perdida pelo atrito como
vento.
a) F: Como a velocidade é constante, a energia cinética também o é.
b) F: Pelo menos motivo do item anterior.
c) F: Se ele desce em relação ao nível de referência, a energia potencial gravitacional não pode
aumentar, e sim diminuir.
d) V: O ciclista está descendo a ladeira, então ele está se aproximando do nível de referência de
energia potencial gravitacional, que é o ponto mais baixo do trajeto. Portanto, a sua EPG está
diminuindo.
e) F: Veja item (d).
6) O gráfico representa a força de interação que age sobre uma partícula em movimento retilíneo
em função da posição da partícula em um
referencial inercial. Entre as posições x = 1,0 m
e x = 3.0 m a energia cinética da partícula:
a) aumentou de 2 joules.
b) diminuiu de 3 joules.
c) aumentou de 3 joules.
d) aumentou de 1 joules.
e) variou de uma quantidade que somente
pode ser determinada conhecendo-se a massa
da partícula.
Resp: C
RESOLUÇÃO
Em um gráfico F x X, o trabalho realizado é obtido pela área sob o gráfico. Podemos ver que a
figura é a de um trapézio, que pode ser dividida em duas: um retângulo e um triângulo.
Área do retângulo: b x h
b = 2 m, h = 1 N  A  2 J
Área do triângulo: b x h ÷ 2
b = 2 m, h = 1 N  A = 1 J
Somamos as duas áreas e obtemos o total: 3 J
Como o trabalho é igual à variação da energia cinética, vemos que essa aumentou em 3 J.
Ec = 3 J
7) Quando um corpo é elevado a uma certa altura do solo, a energia despendida para se
conseguir tal intuito:
a) acumula-se, no corpo, sob a forma de energia interna.
b) é igual à variação da energia cinética do corpo.
c) é nula, pois a resultante média das forças na elevação é nula.
d) fica armazenada no corpo sob a forma de energia potencial gravitacional.
e) transforma-se em calor durante a sua subida.
Resp: d
RESOLUÇÃO
a) F: A energia interna de um corpo está relacionada à sua temperatura.
b) F: A variação da energia cinética do corpo é igual ao trabalho realizado sobre ele.
c) F: Justificativa sem sentido.
d) V: O trabalho de elevar-se um corpo acima de um nível de referência fornece energia potencial
gravitacional a ele.
e) F: Se fosse transformado em calor a força que atua contra o peso não seria conservativa.
8) Daniel está brincando com um
carrinho, que corre por uma pista
composta de dois trechos retilíneos – P
e R – e dois trechos em forma de
semicírculos – Q e S –, como
representado nesta figura:
O carrinho passa pelos trechos P e Q
mantendo o módulo de sua velocidade constante. Em seguida, ele passa pelos trechos R e S
aumentando sua velocidade. Com base nessas informações, é CORRETO afirmar que a
resultante das forças sobre o carrinho
a) é nula no trecho Q e não é nula no trecho R.
b) é nula no trecho P e não é nula no trecho Q.
c) é nula nos trechos P e Q.
d) não é nula em nenhum dos trechos marcados.
Resp: B
RESOLUÇÃO
Trecho P: MRU: a resultante das forças é nula
Trecho Q: MCU: existe a força centrípeta, causada pelo atrito, que faz com que o carrinho faça a
curva, então a resultante das forças não é nula.
Trecho R: MRUV: a resultante das forças não é nula, porque a velocidade linear está aumentando.
Trecho S: MCUV: a velocidade aumenta em módulo, então existe força tangencial, e o carrinho faz
curva, então existe aceleração centrípeta.
9) O esquema ao lado mostra um elevador vertical de peso P = 5.000
N. Examine-o. Sabendo-se que a força T = 5.000 N e desprezando-se
os atritos, pode-se concluir que o elevador está
A) parado.
B) parado ou em MRU.
C) subindo. acelerado.
D) descendo retardado.
Resp: B
RESOLUÇÃO
Como a tensão T tem a mesmo módulo e sentido contrário a peso P, há equilíbrio de forças. Então
o elevador pode estar parado ou em MRU.
10) Um paraquedista, alguns minutos após saltar do avião, abre seu paraquedas. As forças que
atuam sobre o conjunto paraquedista/equipamentos são, então, o seu peso e a força de
resistência do ar. Essa força é proporcional à velocidade. Desprezando-se qualquer interferência
dos ventos, pode-se afirmar que,
a) a partir de um certo momento, o paraquedista descerá com velocidade constante.
b) antes de chegar ao chão, o paraquedista poderá atingir velocidade nula.
c) durante toda a queda, a força resultante sobre o conjunto será vertical para baixo.
d) durante toda a queda, o peso do conjunto é menor do que a força de resistência do ar.
Resp: A
RESOLUÇÃO
a) Correta. A partir de um certo instante a resultante das forças que atuam sobre o conjunto se
torna nula, fazendo com que fique com velocidade constante.
b) Errada. Se sua velocidade for nula ele ficará parado no ar.
c) Errada. Se a força resultante sobre o conjunto será vertical para baixo, haverá aceleração nesse
sentido e a velocidade vai aumentar cada vez mais.
d) Errada. Se durante toda a queda, o peso do conjunto é menor do que a força de resistência do
ar, a resultante das forças será direcionada na vertical, para cima, então o conjunto vai subir e
não descer.
11) Uma partícula cai na atmosfera terrestre desde o
repouso e, antes de chegar ao solo, atinge a
velocidade terminal, tudo conforme o gráfico v x t ao
lado, em que a velocidade é considerada positiva,
quando tiver o sentido de cima para baixo. A seguir,
ilustramos cinco possíveis representações das forças
que agem sobre essa partícula durante seu
movimento. P representa a força peso, e F representa
a força de resistência do ar.
AS PESSOAS QUE TIVERAM ESSA QUESTÃO COMO OBRIGATÓRIA OU A ESCOLHERAM
COMO OPTATIVA RECEBERÃO O PONTO REFERENTE A ELA.
As representações corretas das forças sobre a partícula nos instantes 0, t1 e t2, nessa ordem,
são:
a) I, V e II
b) I, II e V
c) I, III e V
d) IV, V e III
e) V, III e I
Resp: C
RESOLUÇÃO
I: (Sim) Corresponde ao momento incial em que o corpo começa a cair, tendo velocidade nula em
t = 0.
II: (Não) A força de resistência do ar é maior do que o peso. Nesse caso a velocidade estará
diminuindo, o que está em desacordo com o gráfico, pois segundo ele, a velocidade sempre
aumenta até atingir o seu valor máximo.
III: (Sim) O peso ainda é maior do que a força de resistência do ar, o que faz com que a
resultante seja vertical para baixo.
IV: (Não) O corpo deixou de ter peso, o que é um absurdo.
V: (Sim) O peso e a força de resistência do ar se equilibram e o corpo passa a se deslocar em
MRU.
12) Um corpúsculo desloca-se em movimento retilíneo e acelerado, de modo que num instante t
sua velocidade é v. Sendo F e a, respectivamente, a força resultante e a aceleração no instante
referido, aponte a alternativa que traz um possível esquema para os vetores v, F e a.
Resposta: C
RESOLUÇÃO
Como o movimento é acelerado, os vetores a e v têm que ter a mesma direção e o mesmo
sentido. Mas sabemos também que os vetores F e a, têm que ter o mesmo sentido. Então, os três
vetores, F, a e v, têm a mesma direção e o mesmo sentido.
13) Para que um bloco de massa igual a 30 g, inicialmente em repouso, adquira uma velocidade
de 10 m/s em exatamente 1,2 s, é necessário aplicar-lhe uma força cujo módulo, em newtons,
deve valer:
a) 0,25
b) 2,5
c) 25
d) 250
e) 2500
Resp: A
RESOLUÇÃO
m = 30 g = 0,03 kg
V0 = 0
V = 10 m/s
t = 1,2 s
Temos que usar a segunda lei de Newton: F = m.a
m
10
V
s  8, 3 m
a

t 1, 2 s
s2
Mas primeiro é preciso determinar a aceleração. Sabemos que
F  m.a  0,03 kg  8,3
m
s2
 F  0,249  F  0,25
N
14) Uma pessoa pesa um sanduíche em uma balança e lê o valor de “200 gramas”. Essa leitura
está equivocada. Qual deveria ser a leitura correta a ser feita pela pessoa?
a) 2.000 N
b) 200 N
c) 2 N
d) 2 kg
Resp. C
RESOLUÇÃO
m = 200 g = 0,2 Kg
P = mg = 0,2 Kg × 10 m/s2  P = 2 N
15) Um astronauta com o traje completo tem uma massa de 120 Kg. Ao ser levado para a Lua,
onde a gravidade é aproximadamente 1,6 m/s2 , a sua massa, em quilograma, e o seu peso, em
Newton, serão respectivamente:
a) 75 e 120
b) 120 e 192
c) 192 e 192
d) 120 e 120
e) 75 e 192
Resp: b
RESOLUÇÃO
m = 120 Kg
gL = 1,6 m/s2
A massa é invariável, portanto: m = 120 Kg
P = m.g  P = m.gL = 120 Kg × 1,6 m/s2  P = 192 N
16) Um automóvel descreve a trajetória abaixo com velocidade escalar constante. Os trechos AB e
CD são retilíneos, enquanto o trecho BC é um arco de circunferência. Dentre os gráficos abaixo,
assinale o que melhor representa a resultante das forças que atuam no automóvel ao longo da
trajetória ABCD.
Resp: C
RESOLUÇÃO
AB: MRU  R = 0
BC: MCU  R  0, porque há aceleração centrípeta
CD: MRU  R = 0
17) Considere que a Lua descreve uma órbita circular em torno da Terra. Assim sendo, assinale a
opção em que estão mais bem representadas a força resultante (
FR
) sobre o satélite e a sua
velocidade ( V ).
Resp.: D
RESOLUÇÃO
A força resultante, que é a força centrípeta, é sempre perpendicular à velocidade.
GABARITO
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
A
B
A
B
D
C
D
B
B
A
C
C
A
C
B
C
D