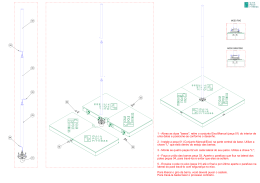
GGH/019
21 a 26 de Outubro de 2001
Campinas - São Paulo - Brasil
GRUPO I
GRUPO DE ESTUDO DE GERAÇÃO HIDRÁULICA – GGH
COMPORTAMENTO DINAMICO DO ROTOR, SOB CONDIÇÕES ESPECIAIS DA VELOCIDADE
CRITICA
Dipl.-Ing. Dr. WALTER SCHEIDL
VA TECH HYDRO
RESUMO
A idéia deste documento é mostrar a influência dos
diferentes parâmetros de desenho da velocidade
crítica de um gerador e para explicar o que está atrás
do termo „velocidade crítica“. De acordo com a
experiência do autor existe várias interpretações
diferentes deste termo, e baseado nisto, o valor da
„velocidade crítica“ é diferente para o mesmo objeto.
Pôr isto é sugerido uma definição para esta
„velocidade crítica“.
PALAVRAS-CHAVE: velocidade crítica do
generador
1. INTRODUÇÃO
Todo cliente que intenciona comprar um gerador
grande ou um motor-gerador requer em sua
especificação técnica, que a primeira velocidade
crítica da máquina deve ter uma determinada
margem de segurança em relação a velocidade de
disparo (off-cam) da turbina. A margem de
segurança varia entre 15 a 25 pôr cento. Na maioria
dos casos está faltando a definição, como deve ser
calculada esta primeira velocidade crítica.
Já que não definida deixa em aberto uma grande
variedade para se aproximar esta, e os resultados
podem variar em uma escala relativamente bem
grande. Assim fica a cargo do ofertante como
calcular este valor. E entre os competidores
internacionais existe diferentes filosofias como
calcular esta.
Neste documento a ELIN (VA TECH HYDRO) quer
primeiramente discutir todas as influências existentes
da primeira velocidade crítica de uma máquina
grande e finalmente gostaríamos de sugerir uma
definição ou um procedimento, como a primeira
velocidade crítica deveria ser calculada.
2. INFLUÊNCIAS DA PRIMEIRA
VELOCIDADE CRITICA DE UMA
MÁQUINA GRANDE
Se olhamos o corte transversal na figura 1 para o
projeto HAEUSLING de um motor-gerador com os
dados - 200MVA, 600 rpm velocidade de disparo
maior que 1000 rpm - se pode ver quais são as
influências da velocidade crítica.
Estas são: a rigidez do próprio rotor, o desenho do
mancal de guia, a rigidez da cruzeta, a rigidez da
conexão da cruzeta e do fundamento, a rigidez do
próprio fundamento, a qual normalmente não se leva
em consideração, em alguns casos a rigidez da
carcaça, e finalmente a influência do peso do rotor.
Antes de começarmos a discutir estes itens
sequêncialmente, deixa me fazer alguns pareceres
(afirmações) sobre o que é a primeira velocidade
crítica. A primeira velocidade crítica é uma
freqüência de ressonância, a qual existe uma
coincidência da velocidade e a freqüência própria de
flexão. Isto é o entendimento normal que alguém
pode ter. Isto significaria que em caso de um sistema
linear sem amortecimento, as vibrações iriam crescer
além de todos limites e finalmente com a destruição
do rotor, com uma pequena força de excitação.
Mas na realidade existe o comportamento não
linear dos mancais, o amortecimento do filme de óleo
e o amortecimento estrutural do próprio material, os
quais limitam as amplitudes de vibrações. Estas
amplitudes são agora diretamente dependentes da
força de excitação e além de tudo a freqüência de
ressonância varia com a magnitude da força de
excitação feito pela relação não linear entre
amplitude, rigidez do filme de óleo e força.
Que tipo de forças podem provocar vibrações? Em
primeiro lugar existem massas não balanceadas, em
segundo lugar existem forças magnéticas não
balanceadas que podem atingir valores muito alto
com algumas falhas no rotor, como pôr exemplo,
curto circuito em 50% dos pólos. Em terceiro existem
forças excitantes da turbina, especialmente da
bomba-turbina operando em uma região de
velocidade acima da nominal, as quais produzem
forças estorasticas (stochastic) muito altas.
3. DESENHO DO ROTOR
O desenho do rotor pôr si próprio tem uma influência
grande na velocidade crítica. O que está diretamente
relacionado é a rigidez própria do rotor, a qual é no
melhor caso usar uma construção sólida da coroa
do rotor . A única desvantagem deste desenho é que
o preço é mais elevado. Pôr isto este tipo de
desenho só é escolhido caso a velocidade de
* Rua Bernardo Guimarães, 2063 – Belo Horizonte – MG – CEP 30140-082
Tel: (31) 3335-1367
e-mail [email protected]
2
disparo muito elevada seja absolutamente
necessária como foi o caso da máquina para o
projeto HAEUSLING, na figura 1.
O desenho da coroa do rotor laminada só pode ser
usada caso a velocidade de disparo não seja tão
elevada. O desenho da coroa do rotor laminada é
mais barato mas tem duas desvantagens, que são a
rigidez mais baixa do rotor e o peso do rotor é mais
elevado do que com uma coroa sólida. A influência
da rigidez e do peso do rotor é mostrado na figura 2
onde a velocidade crítica para diferentes tipos de
desenhos do rotor para a máquina de HAEUSLING
são calculadas em relação a rigidez dos mancais.
4. DESENHO DOS MANCAIS
Para máquinas de alta velocidades a ELIN (VA
TECH HYDRO) utiliza somente mancais guia com
segmentos ajustáveis . É essencial que o suporte
para o segmento do mancal seja tão rígido quanto
possível. Tal suporte é mostrado na figura 3. A
rigidez e o comportamento de amortecimento do
filme de óleo do mancal são mostrados nas figuras 5
e 6. Os cálculos são baseados na geometria do
mancal, o qual é mostrado na figura 4. A figura 5 e 6
para o mancal guia superior e inferior mostra que
existe uma relação extremamente não linear entre
excentricidade do eixo com o mancal e a força do
mancal guia
O que é realmente crítico para o mancal
propriamente dito e para a máquina são somente a
magnitude das forças que são capazes de destruir o
mancal e causar alguns estragos no pino giratório do
rotor. Tais forças altas, as quais estão relacionadas
para valores extremamente altos da excentricidade
do mancal, a rigidez do filme de óleo em si próprio é
praticamente infinito.
Pôr isto, para estados realmente críticos da
máquina, não é necessário levar em consideração
nenhuma elasticidade do filme de óleo. O valor
figurativo sempre utilizado da elasticidade de um
micrômetro pôr tonelada , que é usado na Europa,
está relacionado para forças de magnitude entre 20
e 30 toneladas pôr mancal guia, o que significa
estado não crítico para a máquina em todo.
Mancal guia para geradores do tamanho de
HAEUSLING pode suportar mais que 200 toneladas
de força sem sofrer nenhum dano. Para tais cargas
alta a elasticidade do filme de óleo diminui em
comparação com todas as outras elasticidade do
sistema de suporte mecânico do rotor.
cruzeta tem que ter uma certa rigidez axial e radial.
No caso do gerador de HAEUSLING, ver figura 1, a
transmissão da força radial para o fundamento é feita
diretamente usando adicionalmente um braço de
expansão, o qual transmite as forças radiais dos
braços da cruzeta diretamente para o fundamento.
Isto é absolutamente necessário para conseguir a
maior rigidez no mancal superior. De outra forma não
seria possível atingir com um tal rotor a primeira
velocidade crítica pôr volta de 1200 rpm.
6. CARCAÇA
A função primordial da carcaça é suporta a paquete
magnético do estator. Com o mancal de escora
acima do rotor também tem a função de transmitir s
forças axiais para o fundamento e se a cruzeta
superior não estiver diretamente conectada ao
fundamento, então também transmitir as forças
radiais para o fundamento. Assim a rigidez da
carcaça é essencial para o desenho quando a
cruzeta superior não tenha conexão com o
fundamento
7. RIGIDEZ DO FUNDAMENTO
O fundamento tem que suportar todas as cargas
produzidas pelo gerador. Para conseguir uma certa
velocidade crítica, situada acima da velocidade de
disparo, o fundamento tem que ter uma determinada
rigidez e deve ser livre de ressonância própria em
toda a região de velocidade onde o gerador pode
operar.
Agora existe diferentes caminhos como levar em
consideração a rigidez do fundamento. Na primeira
calculação linear mostrada na figura 7 levamos em
conta a rigidez do filme de óleo, a rigidez do mancal,
rigidez da cruzeta e a rigidez do fundamento mas
sem influência entre os diferentes níveis do
fundamento. O resultado é uma velocidade crítica de
1244 rpm.
Se levamos em consideração que o próprio
fundamento tem algum comportamento dinâmico,
isto significa que o fundamento é influenciado pela
sua massa própria e se levamos em consideração,
que deslocamentos nos diferentes níveis de
conexões entre o gerador e o fundamento não são
completamente independente uma da outra, de
acordo com a figura 8, o resultado da velocidade
crítica , usando o modelo de calculação da figura 9, é
então 1182 rpm, o que é um valor muito bem
próximo do medido de 1200 rpm com pequena força
de excitação parado e quase sem filme de óleo.
5. DESENHO DA CRUZETA
A finalidade da cruzeta do mancal é de transmitir as
cargas para o fundamento. Isto significa, que a
Se calculamos com precisão, isto é, usando modelos
bem realísticos para o calculo, então a margem de
3
segurança entre a velocidade crítica e a velocidade
de disparo (off-cam) não necessita ser maior que
15%. Com base em experiência e medições feitas
em plantas sabemos que nossos valores estimados
para a rigidez dos componentes do gerador são tão
corretos como são na realidade.
De uma outra forma, o fundamento tem que ter a
qualidade estimada de rigidez. Senão a primeira
velocidade crítica teria que ser menor que a
estimada.
8. PESO DO ROTOR
Como já vimos na figura 2 existe uma grande
influência do peso do rotor para a determinação da
primeira velocidade crítica. É bastante importante
quando o cliente está interessado em um motorgerador de 350- 400 MVA com uma velocidade
nominal de 500 rpm e uma velocidade de disparo
720 – 750 rpm e se ainda é exigido um gerador
resfriado a ar com uma coroa polar laminada. Neste
caso não é tão fácil calcular uma máquina como
esta, que preenche todos estes requisitos, porque o
peso do rotor atingiria um valor muito alto, mais que
350 toneladas, e então o desenho seria bastante
cerrado com limite de possibilidade.
A única possibilidade seria deixar o desenho com
uma coroa laminada, e mudar para uma coroa tipo
disco ou melhor ainda com uma coroa sólida com
resfriamento a ar. Uma outra possibilidade para
diminuir o peso do rotor é mudando o sistema de
resfriamento e escolhendo um resfriamento
diretamente com água , que neste caso possa ser
realizado.
9. COMPORTAMENTO DINAMICO DE
MOTOR-GERADOR DE TAMANHOS
ELEVADOS (Cálculos não lineares)
A figura 10 mostra o comportamento do rotor com
uma folga de 0,4 mm para o mancal guia superior e
0,3 mm para o mancal guia inferior. Força de
excitação do rotor correspondente não balanceada
qualidade 4, definida na figura. Figura 11 mostra o
comportamento dinâmico do rotor com folgas radiais
diferentes e com uma foça de excitação não
balanceada qualidade 4.
Se pode ver claramente que existe ressonâncias
para velocidades relativamente baixas,
especialmente com folgas grandes do mancal. Mas
relativamente para estas ressonâncias as forças nos
mancais são relativamente baixas.. Pôr isto existe
ressonâncias mas não há estado crítico na máquina.
Se calculamos agora a mesma situação com
diferentes valores para a folga do mancal mas com
forças não balanceadas de acordo com Q10,
obtemos resultados como mostrado na figura 12.
Agora os valores das forças no mancal são bastante
altas especialmente para velocidades elevadas. Esta
são menores para pequena folga do mancal do que
para grande folga do mancal.
Assim para bom comportamento dinâmico de
grandes máquinas e para um seguro e homogêneo
funcionamento na região de velocidade nominal e
sobrevelocidade é necessário e essencial que o
mancal seja ajustavel. Este ajustamento da folga do
mancal do gerador é feito durante o
comissionamento em um ponto ótimo para um
funcionamento homogêneo da máquina.
10. A VELOCIDADE CRÍTICA
Como mencionado anteriormente diferentes clientes
e diferentes produtores de geradores tem diferentes
pontos de vista no que diz respeito ao termo
“velocidade crítica”. Vamos tentar fazer uma
definição razoável, como calcular esta velocidade
crítica, assim que para um lado tenha uma boa
correspondência com a realidade e pôr outro lado
utilize uma calculação linear aproximada. Como uma
base para isto mostramos na figura 13 uma tabela
com valores para a velocidade crítica baseada em
diferentes suposições.
O primeiro valor foi calculado com mancal rígido
como era feito a 30 ou 40 anos atras. Esta
idealização para o gerador leva a valores não
realístico muito alto para a velocidade crítica e não é
mais usado hoje em dia.
O segundo valor foi calculado com uma rigidez linear
para a parte do gerador com o fundamento rígido e
tem um resultado de 1295 rpm.
O terceiro valor foi calculado com uma rigidez linear
e levando em consideração a rigidez do fundamento
mas sem influência do peso do fundamento, com
resultado de 1244 rpm.
E se adicionalmente levamos em consideração o
chamado peso completo e a matriz de rigidez do
fundamento e do gerador, a velocidade crítica atinge
um valor de 1182 rpm.
Mas para todos estes valores se incluímos uma
elasticidade para o filme de óleo de 0,1 micrômetro
pôr KN, o qual é um maleável filme de óleo e relativo
a este filme de óleo há uma força do mancal de 20 a
30 toneladas.
Tendo assim um maleável filme de óleo e assim uma
pequena força do mancal não seria correto a
palavra crítica. Porque crítico significa realmente
crítico e isto somente é o caso quando as forças dos
mancais se tornam valores extremamente altos.
4
Valores este de pelo menos 200 toneladas pôr
mancal.
Para tais forças tão altas a elasticidade do filme de
óleo é praticamente zero. Respeitando isto nos leva
para o próximo valor de uma ressonancia critica real
de 1270 rpm, onde levamos em consideração o
comportamento linear de todas rigidez e um filme de
óleo absolutamente rígido. Isto corresponde bem
com o valor de pico da ressonância para uma
calculação não linear, considerando também uma
matriz de peso para o fundamento, como mostrado
na figura 12
Nos sugerimos que no caso que o cliente espera pôr
uma margem de segurança relativamente alta de 20
a 25% entre a primeira velocidade crítica do rotor e a
velocidade de embalamento (off cam) da turbina,
então deverá ser calculado de acordo com esta
suposição. Na maioria das especificações chinesas o
cliente pergunta pôr uma primeira velocidade crítica
20 a 25% acima da velocidade de embalamento.
Neste caso deve assumir comportamento linear da
rigidez e esquecer sobre a elasticidade do filme de
óleo nos mancais de guia. Pensamos que esta
suposição seja correta e aceitável para o calculo da
primeira velocidade crítica se requerido uma margem
de segurança de 20 a 25%.
Todo outro método de calculação mais sofisticados
só devem ser usados quando a margem de
segurança é muito pequena. Significa entre 10 a
15%. Em todos estes casos é absolutamente
necessário calcular tão realístico quanto possível o
que a VA TECH HYDRO (ELIN) é capaz.
Figura 1 :
Motor-gerador HAEUSLING, tipo Ssv 435/10-260
U=19500 V, f=50 Hz, n=600 rpm
P=200 MVA, cosphi=0,9, I=5922 A
Nmax=1050 rpm, J=260000 Kgm²
11. CONCLUSÃO
Neste documento vimos as diferentes influências na
velocidade crítica e em conseqüência também o
comportamento dinâmico dos rotores de grandes
geradores e motor-gerador respectivamente e
finalmente sugerimos uma definição como a primeira
velocidade crítica deve ser calculada.
A intenção do autor é que depois do conhecimento
deste documento o cliente deverá definir o que deve
ser levado em consideração quando se tem que
calcular a primeira velocidade crítica, para assim o
cliente e os ofertantes tenham uma base de
comparação e o mesmo entendimento de como
calcular a velocidade crítica.
12. REFERENCIAS BIBLIOGRAFICAS
Dipl. Ing. Dr. Heinrich Guenther EICKHOFF:
Rotordynamik von hydraulischen Turbosätzen in
Pumpspeicheranlagen, Untersuchungen zu den
stationären und transienten Biege- und
Torsionsschwingungen von Wellensträngen solcher
Maschinen mit nichtlinearer Lagerung und mit
Fundamenteinfluß ( Dinâmica do rotor do conjunto
hidráulico turbogerador em plantas de
bombeamento, estudo estacionário e transientes de
vibrações de flexão e torção no eixo com
comportamento não linear do mancal e influência do
fundamento)
Tese de doutorado, Universidade Técnica de Graz,
Austria
Dr. EICKHOFF trabalhou para a ELIN em Weiz e
hoje já falecido.
Figura 2: Primeira velocidade crítica em função da elasticidade do mancal
(elasticidade do mancal guia superior 1,5 vezes da elsasticidade
do mancal guia inferior)
5
Figura 3: Desenho do mancal guia
1- Eixo
2- Trilho de guia
3- Abertura de compensação de ar comprimido
4- Cruzeta
5- Câmara de óleo
6- Empanque para o anel de ar
7- Tampa do mancal com empanque para o anel de ar
8- Segmento do mancal guia
9- Assento e casca esférica
10- Chave de ajustamento
11- Anel de Empaque
Figura 4: Geometria do mancal
Movimento do eixo
n
ML
Centro do mancal
Número de segmentos
b
Espessura do segmento
MZ
Centro do eixo
d
Diâmetro do mancal
η
Viscosidade dinâmica do óleo
Ω
Velocidade angular do eixo
rs
Raio do segmento
SZ
Força relativa do eixo
σ = rb − r
Folga radial do mancal
KZ
Força do eixo
α
Angulo do segmento
rb
Raio do círculo de fixação
d3 ×b ×η ×Ω
KZ =
4×δ2
Figura 5: Mancal guia superior do gerador
Figura 6: Mancal guia inferior do gerador
n
b
d
β = b/d
α
α1/α
τV =
rs − r
rb − r
12
256 mm
1400 mm
0,1829
20,1°
0,5
1
n
b
d
β = b/d
α
α1/α
τV =
rs − r
rb − r
10
296 mm
1150 mm
0,2574
28,2°
0,5
1
6
Suporte para a cruzeta superior
Suporte para o estator
Suporte para a cruzeta inferior
.
. 0012
.  K1
x1  006
002


.
.
.  K2
x2 =  002
005
003
.
.
.  K3
x3 0012
003
006
Figura 8
Figura 7 Primeira velocidade crítica
Filme de óleo do mancal superior e inferior do gerador
Mancal e cruzeta superior
Suportes da cruzeta incluindo as arruelas
Carcaça e estator
Mancal e cruzeta inferior
Mancal superior da turbina
Mancal inferior da turbina
Mancal guia de acoplamento hidráulico
0,1 µm/kN
0,4 µm/kN
0,057 µm/kN
0,42 µm/kN
0,3 µm/kN
0,95 µm/kN
0,6 µm/kN
0,69 µm/kN
Figura 10 Forças não balanceadas de
acordo com Q4 (VID 2060)
Q=ex (e=excentrentricidade do centro de
gravidade [mm])
( =velocidade angular [1/seg])
Figura 9: Primeira velocidade crítica
Figura 11 Forças não balanceadas de
acordo com Q4 (VID 2060)
Q=ex (e=excentrentricidade do centro
de gravidade [mm])
( =velocidade angular [1/seg])
Figura 12 Forças não balanceadas de acordo com Q10 (VID 2060)
Q=ex (e=excentrentricidade do centro de gravidade [mm])
( =velocidade angular [1/seg])
Figura 13 Comparação de velocidades críticas
Valor
Comentários
Tudo rígido (mancais, cruzetas, fundamento)
Variante
2049 rpm
não é dominado pelo gerador
Rigidez linear fundamento rígido ( com matriz
de pesos da cruzeta e fundamentos)
1295 rpm
dominado pelo gerador
Rigidez linear incluindo fundamento ( sem matriz
de pesos da cruzeta e fundamentos)
1244 rpm
dominado pelo gerador
Rigidez linear ( com matriz de pesos do
fundamento e cruzeta, com matriz rigidez
do fundamento)
1182 rpm
dominado pelo gerador
Rigidez linear filme de óleo rígido ( com matriz
de pesos do fundamento e cruzeta,
com matriz rigidez do fundamento)
1270 rpm
dominado pelo gerador
Valores medidos (eixo não rodando, sem folga
Radial no mancal)
1200 rpm
dominado pelo gerador
Não linear filme de óleo e todas rigidez
Lineares ( com matriz de pesos do
fundamento e cruzeta, com matriz rigidez
do fundamento)
ver figura 10,
11 e 12
depende do filme de óleo
(não linear) e forças de excitação