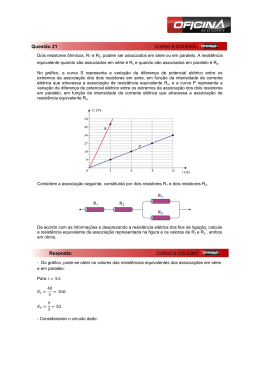
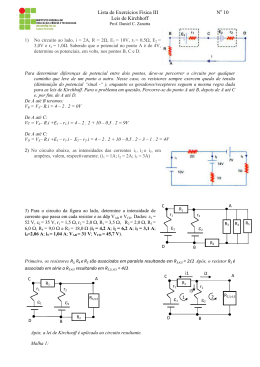
COMPONENTES ELETRÔNICOS
Os componentes eletrônicos dividem em três grupos distintos: ativos, passivos e não definidos.
- Ativos: podem causar amplificação de sinais, corrente ou tensão nos circuitos onde se
encontram. Fabricados de materiais semicondutores como o silício e o germânio. Exemplo:
Transistor.
- Passivos: tem como função criar atenuação nos circuitos onde estão conectados.
Normalmente possuem apenas dois terminais e são fabricados basicamente com materiais
condutores e isolantes. Basicamente são três os componentes passivos, resistores, capacitores e
bobinas.
- Não definidos: sensores, transdutores, osciladores e controladores.
RESISTORES
Ao trabalharmos com resistência elétrica em um circuito eletrônico conseguimos controlar a
corrente e a tensão de um circuito. Outro efeito da resistência elétrica em um circuito é a
transformação da energia elétrica em energia térmica (efeito joule), como vemos nos chuveiros
elétricos.
Como já vimos, qualquer material apresenta certo grau de resistência à passagem de
elétrons, ou seja, à passagem da corrente elétrica. O resistor é o componente eletrônico
especialmente concebido para este fim. Os resistores são graduados conforme o grau de resistência
que possuem na unidade de resistência ohm (Ω). Como atenuam a corrente são componente
classificados como passivos. São fabricados em vários formatos e materiais conforme veremos
adiante e quando percorrido por uma corrente elétrica além da capacidade de atenuação da
corrente elétrica, realizam trabalho, transformando energia elétrica em energia térmica. Através
deste trabalho realizado medimos sua potência em watt (W).
Os resistores estão inseridos em 99,9% dos circuitos eletrônicos, a fim de controlar a
corrente ou tensão de outros componentes sensíveis, assim, podem estar dispostos em qualquer
configuração de circuito como já vimos anteriormente (em série, paralelo ou circuitos mistos), cujas
leis de Ohm e Kirchhoff são aplicáveis para análise e estudo dos resistores.
A simbologia aplicada para resistores normalmente é aplicada em dois formatos, como
segue abaixo:
A partir destes dois formatos, derivam a simbologia de resistores do tipo variáveis, ou seja, a
resistência nominal dos resistores varia com algum fator externo, como veremos adiante.
ASSOCIAÇÃO DE RESISTORES
Podemos associar resistores em circuitos nas três formas possíveis, em série, paralelo e
misto. Dominando este assunto poderemos realizar cálculos pertinentes, a fim de projetos ou
entendimento funcional do circuito. Na prática podemos também substituir uma associação de
resistores por outra equivalente, ou por apenas um resistor, muito útil quando não temos disponível
um valor original e precisamos consertar ou desenvolver um projeto.
ASSOCIAÇÃO DE RESISTORES EM SÉRIE
A associação de resistores em série é feita de modo que o fim de uma resistência fique
ligado com o começo da outra, ou seja, os resistores ficam “enfileirados”. Neste tipo de circuito
temos somente um caminho para a corrente elétrica. Exemplo:
A resistência total ou equivalente do circuito será a soma das resistências parciais e,
portanto, a resistência total será maior que a maior resistência:
Req = R1 + R2 + R3 + ... + Rn
Portanto, em nosso exemplo a resistência equivalente será de:
Req = 10 + 30 + 20 + 40 = 100 Ω
Em circuitos em série usamos a Lei de Kirchhoff para Tensão, que diz:
“No circuito em série, a soma das quedas de tensões parciais é igual a tensão aplicada
neste circuito.”
Exemplo:
De acordo com a Lei de Kirchhoff:
Utotal = U1 + U2 + U3 ++... + Un
Para nosso exemplo temos que:
U1 = 1,2 V; U2 = 3,6 V; U3 = 2,4 V; U4 = 4,8 V
Utotal = 1,2 + 3,6 + 2,4 + 4,8 = 12 V, demonstrando a Lei de Kirchhoff.
Como só temos um caminho para a corrente elétrica, notamos que esta é a mesma para
qualquer ponto do circuito.
Nos circuitos em série a potência da associação será igual a do resistor de menor potência.
Como trabalhamos com corrente, tensão e resistência, para resolução de problemas pertinentes a
circuitos, e potência dissipada, adotaremos também a Lei de Ohm (U = R x I) e a fórmula para cálculo
de potência (P = U x I).
NOÇÃO SOBRE CONDUTÂNCIA
Ao contrário da resistência, a condutância mede a facilidade que um material oferece ao
fluxo da corrente elétrica. Em outras palavras, a condutância é o contrário da resistência:
G = 1/R [S] siemens
ASSOCIAÇÃO DE RESISTORES EM PARALELO
A associação de resistores em paralelo é feita de modo que todos os resistores fiquem
ligados em um mesmo ponto ou “nó”. Neste tipo de circuito a corrente elétrica tem tantos caminhos
quanto forem as resistências associadas.
Vejamos o esquema abaixo:
A resistência equivalente do circuito será igual a soma de suas condutâncias, de modo que a
resistência final seja menor que a menor resistência do circuito:
GT = G1 + G2 + G3 + G4
Substituindo condutância por resistência:
1/Req = 1/R1 + 1/R2 + 1/R3 + ...+ 1/R4
Req = 1/ (1/R1 + 1/R2 + 1/R3 + ...+ 1/R4)
Para nosso exemplo, a resistência equivalente será:
Req = 1/ (1/10 + 1/30 + 1/20 + 1/40) = 4,8 Ω
Na grande maioria dos casos temos somente dois resistores em paralelo na associação. Se
esse for o caso temos uma fórmula deduzida simplificada:
RT = R 1 x R2 / R 1 + R2
EXEMPLO:
Neste exemplo temos que Req
=
= 149,8 ohms.
Se em uma associação de resistores em paralelos tivermos somente resistores de mesmo
valor, podemos ainda adotar a seguinte forma:
Req =
, onde R é valor do resistor e n é a quantidade de resistores deste mesmo valor.
EXEMPLO:
Neste exemplo temos que Req =
= 16,7 ohms
Para a associação de resistores em paralelo podemos associar a Lei de Kirchhoff para
correntes, onde trata circuitos em paralelo:
“Num circuito paralelo, a corrente total é a soma das correntes parciais.”
Assim, a soma das correntes que chegam a um nó (ponto de ligação), é igual a soma das
correntes que saem.
Exemplo:
Pela 1ª Lei de Kirchhoff podemos escrever:
Itotal = I1 + I2 + I3 + ... + In
Neste nosso exemplo podemos provar que a corrente total é 2,5 A, achando a resistência
equivalente e dividindo a mesma pela tensão ou encontrando as correntes parciais em cada ramo
aplicando a lei de Kirchhoff para correntes.
Nos circuitos em paralelo a tensão aplicada é a mesma em qualquer resistência do circuito.
Nos circuitos em paralelo a potência da associação será igual a soma das potências de cada
resistor. Como trabalhamos com corrente, tensão e resistência, para resolução de problemas
pertinentes a circuitos, e potência dissipada, adotaremos também a Lei de Ohm (U = R x I) e a
fórmula para cálculo de potência (P = U x I).
ASSOCIAÇÕES MISTAS DE RESISTORES
Em um circuito temos associações mistas de resistores quando temos parte do circuito com
associações em série e parte com associações em paralelo. Para resolvermos circuitos com
associações mistas temos que resolver o circuito parte por parte de modo a simplificar o circuito
para uma associação única.
EXEMPLOS DE ASSOCIAÇÃO MISTA DE RESISTORES: