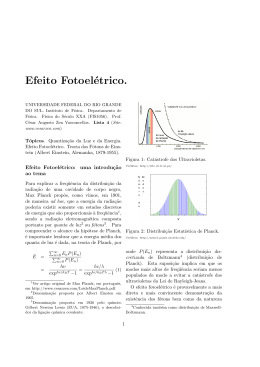
41
2.2 Efeito fotoelétrico
–
V
+
fótons
e−
Corrente
FIGURA 13 - Circuito esquemático do efeito fotoelétrico.
sobre um deles luz ultravioleta. Ironicamente, o efeito fotoelétrico por ele descoberto e considerado como uma “observação de menor importância” levou
a uma reformulação completa no conhecimento das ondas eletromagnéticas,
demonstradas no mesmo experimento.
O que é, afinal, o efeito fotoelétrico? É o fato de que energia eletromagnética,
seja na forma de raios X, luz ultravioleta ou luz comum incidindo sobre
metais, provoca a ejeção de elétrons de suas superfı́cies.
Como a teoria clássica explica esse fenômeno? Ela sugere que a luz incidente chega na forma de uma onda eletromagnética. Se usarmos um feixe
uniforme, sua energia estará contida em toda frente de onda (como ocorre
com uma onda mecânica na água, por exemplo). Quanto mais intensa a
~ eB
~ em qualquer ponto da frente de
luz, maior a amplitude dos campos E
onda, e maior será a energia que a onda deposita no metal por segundo.
Esses campos exercem forças sobre os elétrons do metal e, eventualmente,
conseguem arrancá-los da superfı́cie. Vamos estimar, dentro desse contexto
clássico, quanto tempo seria necessário para a liberação de um elétron.
Para concretizar as idéias, consideremos uma radiação com intensidade de 1
mW/m2 , que incida num metal para o qual a energia necessária para libertar
o elétron das forças que o prendem ao material (função trabalho, φ) seja 4 eV.
Supondo uma distribuição contı́nua e uniforme de radiação, vamos estimar
o tempo necessário para que o elétron absorva a energia necessária (4 eV) e
escape.
O diâmetro do átomo é da ordem de 0,3 nm. A energia por unidade de
tempo, P , que incide num único átomo é
2
P = Id = (10
−3
Js
= 6 × 10−4 eV/s.
−1
2
m ) · (3 × 10
−10
2
m) ×
1 eV
1, 6 × 10−19 J
42
2 Fenômenos que deram origem à mecânica quântica
Então, o tempo necessário para absorver 4 eV será
∆t =
4 eV
4 eV
=
= 7 × 103 s,
P
6 × 10−4 eV/s
aproximadamente duas horas! No entanto, os experimentos feitos até hoje
foram incapazes de detectar qualquer atraso entre a incidência da luz e a
ejeção do elétron!
O próximo fı́sico a investigar de forma mais sistemática o fenômeno foi Phillip
Lenard (1862-1947), que trabalhara com Hertz. Lenard montou uma experiência esquematizada na Fig. 13: a luz arrancava cargas elétricas de uma
placa emissora, e estas eram aceleradas por uma diferença de potencial e
coletadas por outra placa. Um amperı́metro registrava a chegada das cargas,
medindo uma corrente elétrica. As conclusões de Lenard foram as seguintes:
1. O efeito fotoelétrico só ocorre a partir de uma determinada freqüência
νmin . Aumentar a intensidade da luz não altera esse fato.
2. A partir do momento em que o fenômeno começa a acontecer, a quantidade de cargas emitidas pela placa metálica é proporcional à intensidade da luz incidente.
3. Para outras freqüências abaixo do valor νmin , o efeito não ocorre, qualquer que seja a intensidade da luz incidente.
Note que quando o potencial é gradualmente diminuı́do, o mesmo ocorre com
a corrente. A partir do gráfico observado, podemos concluir que elétrons
chegam à placa coletora mesmo se a diferença de potencial for nula, o que
significa que ganharam energia mais do que suficiente para se libertarem do
metal. O restante é transformado em energia cinética. Por isso, mesmo
na ausência de uma diferença de potencial, a corrente medida não é nula.
Evidentemente, se o sinal da diferença de potencial for invertido, surgirá
uma força oposta à velocidade dos elétrons, levando a um decréscimo da
corrente ainda maior. A uma dada diferença de potencial nessas condições,
V0 – chamado de potencial de retardo e que depende de cada material – a
corrente fotoelétrica cessa.
A existência de um potencial mı́nimo, V0 , independente da intensidade da
luz incidente, também era embaraçosa, uma vez que, classicamente, isso não
deveria ocorrer.
Infelizmente, os dados de Lenard não eram suficientemente precisos para
medir a forma funcional do potencial V0 como função da freqüência. Como,
então, interpretar esses resultados?
43
2.2 Efeito fotoelétrico
Para frear um elétron com energia cinética
1
K = me v 2
2
(2.22)
é preciso usar um potencial de freamento V0 , tal que
K = eV0 .
(2.23)
Então, o potencial de freamento V0 deve estar associado a elétrons com
direção de movimento perpendicular ao cátodo e com energia cinética máxima
1
2
= eV0 .
Kmáx = m2 vmáx
2
(2.24)
Por conservação de energia, essa energia cinética máxima deve corresponder
à energia fornecida pela luz, descontada a função trabalho φ. Temos, então,
1
2
me vmáx
= eV0 = E − φ.
2
(2.25)
De acordo com a teoria clássica, E é proporcional à intensidade da onda
e, portanto, esperarı́amos que, à medida que a intensidade aumentasse, E
aumentasse simultaneamente e, por conseqüência, V0 . Não é o que se observa.
Num trabalho publicado em 1905, Albert Einstein (1879-1955) propôs uma
teoria do efeito fotoelétrico baseada no trabalho anterior de Planck – a radiação eletromagnética de freqüência ν consiste de quanta de energia
E = hν.
(2.26)
Essa hipótese explicaria imediatamente o fato de que não se observava atraso
na emissão dos fotoelétrons. Um quantum de luz (o fóton) transfere toda sua
energia a um único elétron. Com essa hipótese, a Eq. (2.25) fica
1
2
me vmáx
= eV0 = hν − φ.
2
(2.27)
Esta é a equação de Einstein sobre o efeito fotoelétrico. Note que essa equação
permite uma verificação independente daquela proveniente da radiação de
corpo negro para o valor de h, uma vez que a inclinação do gráfico (linear)
V0 × ν é simplesmente h/e.
Em 1915, Robert Andrews Millikan (1868-1953) comprovou a equação de
Einstein, medindo V0 como função da freqüência de corte (Fig. 14). Note
44
Energia cinética máxima (eV)
2 Fenômenos que deram origem à mecânica quântica
♦
3
2.5
♦
2
♦
1.5
♦
1
0.5
♦
♦
Kmáx
Equação da reta:
= −1, 81 + 4, 12 × 10−15 ν
0
40
50
60
70
80
90
100
13
freqüência, ν (×10 Hz)
110
120
FIGURA 14 - Dados do efeito fotoelétrico para o sódio, obtidos por Millikan
em 1916 (R. A. Millikan, “A direct photoelectric determination of Planck’s
‘h’ ”, Phys. Rev. 7, 355 (1916))
que a equação do efeito fotoelétrico não é uma demonstração da existência
de fótons, apenas é compatı́vel com essa idéia.
Em 1913, Einstein foi proposto como membro titular à Academia Prussiana
de Fı́sica. Ele tinha, então, 34 anos. A proposta terminava da seguinte
forma:
“Pode-se afirmar que não há praticamente nenhum dos grandes
problemas fı́sicos ao qual Einstein não tenha dado alguma notável
contribuição. Que ele, às vezes, tenha errado o alvo em suas especulações, como por exemplo, em sua hipótese dos quanta de
luz, não pode realmente ser tomado como uma acusação muito
séria contra ele, pois não é possı́vel introduzir idéias verdadeiramente novas, mesmo nas circunstâncias mais exatas, sem correr
alguns riscos de vez em quando.”
Em 1921, após a comprovação de sua teoria sobre o efeito fotoelétrico, através
dos experimentos de Millikan, Einstein recebeu o prêmio Nobel de fı́sica4
4
Nota: A resistência dos fı́sicos em aceitar a idéia de que a luz era composta por fótons
tinha sua razão de ser. Os fenômenos tı́picos da fı́sica ondulatória (interferência, difração
etc) eram bem conhecidos e a idéia de associar a luz com partı́culas poderia não sobreviver
a ter que explicar esses fenômenos também.
45
2.2 Efeito fotoelétrico
(principalmente por essa teoria).
Exemplo 2.5 : Na Fig. 14 estão os dados obtidos por Millikan para
o sódio. Obtenha, a partir deles, o valor da constante de Planck em
unidades de J·s.
Da fórmula de Einstein, temos
Kmáx = hν − φ.
Usando a informação dada no gráfico, temos diretamente que
h = 4, 12 × 10−15 eV · s,
ou seja,
h
= 4, 12 × 10−15 V · s.
e
Sabendo que e = 1, 6 × 10−19 C, obtemos para a constante de Planck
h = 6, 59 × 10−34 J · s.
O valor hoje conhecido para h é
h = 6, 6262 × 10−34 J · s.
Podemos também ler diretamente a função trabalho do sódio. Ela vale
φ = 1, 81 eV.
Exemplo 2.6 : Fótons de comprimento de onda 220 nm incidem
sobre um alvo metálico e liberam elétrons com energias cinéticas na
faixa de 0 a 6, 1×10−19 J. Determine a freqüência mı́nima para a qual
elétrons ainda são emitidos.
Os elétrons que saem com maior energia são aqueles que se encontram
na superfı́cie do metal e cuja energia necessária para serem liberados
é igual à função trabalho do material. Logo, podemos encontrar a
função trabalho através da equação
φ = hν − Kmáx =
hc
− Kmáx = 2, 93 × 10−19 J.
λ
A freqüência mı́nima é dada pela energia mı́nima que o fóton deve ter
para conseguir arrancar um elétron do metal e que é, portanto, igual
à função trabalho. Assim
νmin =
φ
= 4, 4 × 1014 Hz.
h
46
2 Fenômenos que deram origem à mecânica quântica
Área da imagem
Invólucro metálico ou cerâmico
Pinos de conexão
Fios de ouro
Contatos
PSfrag replacements
Amplificador
Registrador serial
FIGURA 15 - Desenho de um CCD.
Sobre uma das aplicações do efeito fotoelétrico – detectores CCD
A sigla CCD quer dizer “dispositivo de carga acoplada” (do inglês ChargeCoupled Device). O detector CCD é um aparelho extremamente sensı́vel
para a detecção da luz. É um chip quadrado, formado por uma matriz de
sensores fotoelétricos, feitos de material semicondutor, distribuı́dos em linhas
e colunas.
Cada um dos pontos da matriz na Fig. 15 é denominado pixel. Assim, cada
sensor do CCD dará origem a um pixel da imagem digital final. Quando um
fóton atinge um desses sensores, um elétron é liberado por meio do efeito
fotoelétrico, e registrado como sendo proveniente daquele determinado pixel.
Como acabamos de ver, quanto mais fótons atingirem um certo pixel, mais
elétrons são liberados. Um sistema eletrônico registra os elétrons, somando
a quantidade total deles, sensor por sensor. Depois de um certo tempo, o
sistema tem informações armazenadas e um mapa que mostra como estão
distribuı́das espacialmente as intensidades luminosas. Temos, assim, uma
imagem digital.
47
2.3 O calor especı́fico dos sólidos
100
Eficiência (%)
CCD
10
Olho humano
1
0
200
300
400
500
600
700
λ (nm)
FIGURA 16 - Gráfico comparativo entre a eficiência de um CCD e do olho
humano.
A eficiência de uma aparelho como esse, se comparado à eficiência do olho humano é enorme (Fig. 16). Atualmente, as mais diversas câmeras fotográficas
e filmadoras digitais utilizam os CCDs como detectores de luz. Também
em astronomia, a vantagem de utilizar um CCD é que, mesmo em regiões
“escuras”, ele consegue somar as contribuições de fóton por fóton ao longo
do tempo. Assim, é possı́vel registrar imagens de objetos cuja radiação que
chega à Terra é muito fraca.
2.3
O calor especı́fico dos sólidos
Após a descoberta de Planck sobre propriedades não usuais da radiação, o
próximo passo foi testar essa hipótese em outros fenômenos.
Um dos passos decisivos para dar suporte às hipóteses de Planck, reforçando
seu caráter fundamental, foi dado por Einstein em 1905 em sua teoria do
efeito fotoelétrico. Um outro passo, também devido a Einstein, foi seu trabalho referente aos calores especı́ficos dos sólidos. Em 1907, Einstein supôs
que a energia de um sólido a temperatura T fosse representada pela energia
média de 3N osciladores de Planck unidimensionais com freqüência ν, para
os quais vale
hν
hi = hν/kT
,
(2.28)
e
−1
48
2 Fenômenos que deram origem à mecânica quântica
e a energia do sólido deve valer, portanto,
hEi ≈ 3N hi .
(2.29)
Dessa hipótese resulta, imediatamente, que
∂hEi
= 3N k
cv =
∂T
hν
kT
2
ehν/kT
ehν/kT
−1
2 .
(2.30)
Para hν kT , essa expressão reproduz o resultado clássico 3N k (Lei de
Dulong-Petit), mas difere do mesmo quando T → 0, pois
cv −−−→ 0 6= 3N k !!
(2.31)
T →0
2.4
Bremsstrahlung
A palavra Bremsstrahlung significa “radiação de freamento” (do alemão bremsen=frear + Strahlung=radiação). É um efeito, de uma certa forma, inverso
ao efeito fotoelétrico: quando elétrons energéticos atingem um alvo denso,
são rapidamente desacelerados e, portanto, irradiam. O espectro resultante
é largo e contı́nuo, e está ilustrado na Fig. 17.
Tanto o efeito fotoelétrico como o Bremsstrahlung só podem ocorrer na presença de alvos suficientemente pesados que possam receber energia e momento. Sabendo que a luz é composta por fótons, o que podemos dizer sobre
essa curva?
Usando a idéia sobre a natureza corpuscular da luz, comprovada pelo efeito
fotoelétrico, Einstein previu que haveria um limite inferior para o comprimento de onda da radiação emitida. Imaginemos um elétron que, inicialmente, incide no alvo com uma energia da ordem de eV, após ser acelerado
por uma diferença de potencial V . Enquanto vai sendo desacelerado dentro
do alvo, ele irradia fótons. A freqüência máxima νmáx (comprimento de onda
mı́nimo λmin ) ocorre quando toda a energia cinética do elétron é irradiada
por um único fóton:
E = hνmáx = eV
eV
h
ch
.
=
eV
⇒ νmáx =
∴ λmin
49
2.4 Bremsstrahlung
Detetor
Colimador
Colimador
Fonte de raios X
PSfrag replacements
Fenda divergente
Suporte rotatório para amostras
PSfrag replacements
Detetor
Colimador
Colimador
Fonte de raios X
Fenda divergente
Suporte rotatório para amostras
Comprimento de onda, Å
FIGURA 17 - Difratômetro θ − 2θ de raios X (acima) e gráfico
Bremsstrahlung de um alvo de molibidênio (abaixo). Os picos da curva
resultam da estrutura atômica do alvo especı́fico.
50
2 Fenômenos que deram origem à mecânica quântica
Exemplo 2.7 : Determine o menor comprimento de onda de raios X
que podem ser emitidos por um elétron quando ele atinge a máscara
metálica na face frontal de um tubo de televisão em cores, que opera
com uma voltagem de 20,0 kV.
ch
(2, 9979 × 108 m/s)(4, 13567 × 10−15 eV · s)
=
eV
20, 0 × 103 eV
= 0, 0620 nm.
λmin =
A existência de uma freqüência máxima foi confirmada experimentalmente
em 1915 por W. Duane e F. Hunt, em Harvard. Nessa experiência também, o
valor de h pode ser determinado. Na ocasião, isso foi feito com uma precisão
melhor do que 4%.
2.5
Efeito Compton
A próxima evidência da realidade dos fótons e o fato de que eles se comportam
como partı́culas, possuindo também um momento bem definido, foi obtido
por Arthur H. Compton (1892-1962) entre 1919 e 1923.
Compton observou o espalhamento de raios X monocromáticos por um alvo
de grafite. Esse alvo possui muitos elétrons pouco ligados, que podem ser
considerados como essencialmente livres. De forma mais quantitativa, a energia dos raios X incidentes é muito maior do que a energia da ligação dos
elétrons.
O experimento foi o seguinte: raios X de comprimento de onda de 0,7 Å
incidiam sobre a grafite, que espalhava essa radiação em todas as direções.
Compton usou um espectrômetro de Bragg para raios X e fez uma análise da
radiação espalhada para diversos ângulos. O resultado de seu experimento
está mostrado na Fig. 18.
A figura nos mostra que a intensidade dos raios X espalhados apresentava
dois picos cuja distância é função do ângulo de observação. O primeiro pico
aparece exatamente no comprimento de onda relativo à radiação incidente,
e o outro tem um comprimento de onda maior. A variação do comprimento
de onda, ∆λ, entre essas duas componentes pode ser escrita como função do
ângulo de espalhamento de forma simples
∆λ = 2, 4 × 10−12 (1 − cos θ) m.
(2.32)
2.5 Efeito Compton
Câmara de
ionização
Cristal de
calcita
Alvo de
carbono
PSfrag replacements
Tubo de raio X
Molibidênio
Kα
FIGURA 18 - Experimento de espalhamento Compton.
51
52
2 Fenômenos que deram origem à mecânica quântica
8
7
λ (10−12 m)
6
5
4
3
2
1
0
0
0.5
1
1 − cos θ
1.5
2
FIGURA 19 - Em seu trabalho original, Compton fez o espalhamento de
fótons de comprimento de onda λ = 2, 2 × 10−12 m por elétrons, e mediu os
comprimentos de onda da radiação espalhada em ângulos de 0◦ , 45◦ , 90◦ e
135◦ . Os dados ajustam uma reta cuja inclinação é hc/me c2 (A. H. Compton,
Phys. Rev. 21, 483 (1921)).
A Fig. 19 mostra os primeiros dados obtidos por Compton. Ele usava fótons
obtidos de decaimento nuclear e mediu o comprimento de luz espalhada a 0◦ ,
45◦ , 90◦ e 135◦ . Os dados mostram que o comprimento de onda da luz espalhada varia linearmente com 1 − cos θ, e que a constante de proporcionalidade
é 2, 4 × 10−12 m.
Compton não apenas demonstrou a precisão da fórmula (2.32), como também
que ela pode ser interpretada de maneira muito simples se a hipótese de
Einstein for levada às últimas conseqüências. Uma conseqüência da teoria
da relatividade restrita de Einstein é que partı́culas que viajam na velocidade
da luz são partı́culas sem massa, cujo momento é dado por
|~
p| =
E
,
c
(2.33)
onde E é a energia total da partı́cula.
Uma outra observação experimental foi importante para as hipóteses de
Compton: o comprimento de onda da radiação espalhada era independente
do material que constituı́a o alvo. Compton supôs que o espalhamento era
devido a colisões entre os fótons e os elétrons do alvo – os átomos como um
todo não participavam do processo a não ser para receber o recuo do elétron.
53
2.5 Efeito Compton
Baseado nesses fatos e hipóteses, Compton formulou seu modelo: um fóton
com energia E0 e momento p0 incide sobre um elétron estacionário, cuja
energia é a sua massa de repouso, isto é, me c2 .
y
p00 , λ00
fóton
elétron
θ
x
E0 , p0
ϕ
p~e
depois
antes
A conservação de energia nos fornece
p0 c + me c2 = p00 c +
p
p2e c2 + m2e c4 .
(2.34)
A conservação de momento, por outro lado, fornece
p0 = p00 cos θ + pe cos ϕ,
0 = −p00 sen θ + pe sen ϕ.
(2.35)
(2.36)
A Eq. (2.34) pode ser reescrita de forma mais conveniente, isolando-se o
termo que contém a raiz quadrada
p
p2e c2 + m2e c4 = p0 c + me c2 − p00 c.
(2.37)
As outras duas equações, multiplicadas por c, fornecem
pe c cos ϕ = p0 c − p00 c cos θ,
pe c sen ϕ = p00 c sen θ.
(2.38)
(2.39)
Elevando ao quadrado e somando as Eq. (2.38) e (2.39), temos
2
p2e c2 = (p0 c − p00 c cos θ)2 + p00 c2 sen2 θ.
(2.40)
Elevando a Eq. (2.37) ao quadrado e isolando m2e c4 , vem
m2e c4 = (p0 c + me c2 − p00 c)2 − p2e c2 ,
(2.41)
que, usando Eq. (2.40), se reduz a
me c2 (p0 c − p00 c) = p0 p00 c2 (1 − cos θ).
(2.42)
54
2 Fenômenos que deram origem à mecânica quântica
Resolvendo, então, para p00 , o momento do fóton espalhado, teremos
p00 c =
me c 2 p 0 c
.
me c2 + p0 c(1 − cos θ)
(2.43)
Essa é a fórmula de Compton que fornece o momento do fóton espalhado, p00 ,
em termos do momento do fóton incidente, p0 , do ângulo de espalhamento,
θ, e da massa do elétron.
Agora vamos reescrever a fórmula de Compton em termos de comprimento
de onda, usando a hipótese de Einstein:
h
p0 c = hν0 ⇒ p0 = .
λ0
Analogamente, p00 = h/λ00 . Substituindo essas expressões na Eq. (2.42),
obtemos
hc
λ00 − λ0 =
(1 − cos θ) = λC (1 − cos θ),
(2.44)
me c 2
com λC (comprimento de onda Compton do elétron) igual a
λC = 2, 426 × 10−12 m = 0, 02426 Å.
(2.45)
A expressão obtida por Compton comprova de maneira quase espetacular a
fenomenologia (cf. Eq. (2.32)).
Vamos, antes de prosseguir, estudar alguns limites da fórmula de Compton:
1. A energia do fóton incidente é muito menor que a energia de repouso
do elétron.
Matematicamente, isto significa que p0 c me c2 . Neste limite, a Eq.
(2.43) dá
p00 ≈ p0 ,
e a energia do fóton não se altera pelo espalhamento. A imagem que
podemos fazer desse limite é que ele corresponde ao fóton sendo espalhado por uma parede. Momento é transferido, mas não energia.
2. Retro-espalhamento (θ = π).
p00 c =
me c 2 p 0 c
me c2 + 2p0 c
No caso de fótons incidentes muito energéticos, p0 c me c2 , teremos
me c 2
=
.
2
Vemos que neste limite, o fóton espalhado deve ter uma energia correspondente à metade da massa de repouso do elétron.
p00 c
55
2.5 Efeito Compton
3. O que aconteceria se a massa do elétron fosse muito maior que h/c ?
Neste caso, podemos aproximar o lado direito da Eq. (2.44) por zero,
e obterı́amos um deslocamento nulo:
λ00 = λ0 .
Este limite explica o aparecimento do primeiro pico nas intensidades
de raios X observadas: a observação desse pico é consistente com um
espalhamento não por um elétron apenas, mas pelo átomo de carbono
como um todo. Como a massa do carbono é quatro ordens de grandeza
maior do que a massa do elétron, o deslocamento correspondente é
desprezı́vel.
A interpretação de Compton seria confirmada anos mais tarde quando foi
feita a observação do elétron de recuo por G. N. Cross e N. F. Ramsey,
em 1950; usando raios γ de comprimento de onda 2,6 MeV, eles mediram o
ângulo de espalhamento do elétron, ϕ, obtendo completa concordância com
os dados de Compton. Um outro experimento posterior (Z. Bay et al., 1955)
mostra que o elétron e o fóton emergentes saem em coincidência, com uma
precisão de 10−11 s.
Confirma-se assim que o espalhamento Compton é completamente compatı́vel
com o espalhamento entre duas partı́culas. A luz se comporta aqui, outra
vez, como uma partı́cula, o fóton.
2.5.1
Distribuição de energia de fótons e elétrons
Vamos retomar a expressão (2.44) e reescrevê-la da seguinte forma
λ00 − λ0 =
4πh
2 θ
2 θ
sen
=
2λ
sen
.
C
me c 2
2
2
O comprimento de onda Compton, λC , pode ser usado para medir o tamanho
de uma partı́cula. Vamos, primeiramente, calcular a energia cinética do
elétron espalhado.
~c 1
1
0
T = hν0 − hν0 =
−
2π λ 0 λ00
(2.46)
2λC sen2 θ/2
.
= hν0
λ0 + 2λC sen2 θ/2
Da expressão acima, vemos que a energia do elétron espalhado é diretamente
proporcional à energia do fóton. Portanto, o efeito Compton só pode ser
56
2 Fenômenos que deram origem à mecânica quântica
observado no domı́nio de pequenos comprimentos de onda (raios X ou raios
γ). Lembre-se que de acordo com a eletrodinâmica clássica não é permitida
alteração de freqüência no espalhamento de luz; é apenas o fato de que a luz
é feita de quanta com momento h/λ e energia hν, que torna isso possı́vel.
Por isso, o efeito Compton confirma a hipótese “granular” da luz e também
a validade da conservação da energia para interação entre a matéria e a luz.
Questões
Potencial de Freiamento (V)
2.1 O gráfico abaixo representa os dados obtidos em uma experiência
de efeito fotoelétrico.
12
10 (100; 10)
8
6
(150; 6)
4
(200; 3,8)
2
0
100
(300; 1,9)
(400; 0,5)
400
150
200
250
300
350
Comprimento de onda (nm)
A partir desses dados, obtenha:
(a) a função trabalho do material do cátodo;
(b) a freqüência de corte;
(c) o valor da constante de Planck (h) em unidades de eV· s .
Exercı́cios
Radiação de corpo negro
2.1 Suponha que você seja um corpo negro a 33◦ C (temperatura externa). Qual é o comprimento de onda no qual você irradia mais
energia por unidade de comprimento de onda?
2.2 Um corpo negro irradia 180 J a 20,0◦ C em 8,00h; qual é a sua
área superficial?
57
Exercı́cios
2.3 Imagine que você queira construir um circuito para operar à temperatura ambiente. Nesse circuito, há um resistor de 100 Ω, que
carrega uma corrente de 1 mA. Estime o tamanho mı́nimo (área
superficial) do resistor, se a sua temperatura não deve exceder
400 K.
2.4 Estime a temperatura do nosso planeta, supondo que a Terra seja
um corpo negro ideal absorvendo energia do Sol.
(Dica: Use o valor da constante solar dada no exemplo 2.3, e
lembre-se que a área banhada pelo sol é dada pelo projeção no
plano perpendicular à radiação incidente.)
2.5 Na lei de deslocamento de Wien, o comprimento de onda máximo
é inversamente proporcional a T ; mas porque ν = c/λ, a freqüência
máxima é diretamente proporcional a T . Como resultado, a
versão em termos de freqüência dessa lei é
νmax = (58, 8 × 109 Hz/K)T.
O intervalo da unidade de freqüência não é igual a uma constante
vezes o intervalo da unidade de comprimento de onda. Mostre que
λmax νmax 6= c.
2.6 Determine a freqüência na qual um corpo negro à temperatura
de 1000◦ C irradiará a maior quantidade de energia por unidade
de freqüência.
(Dica: Use a discussão do problema anterior.)
2.7 Um corpo negro está à temperatura de 6000 K. Em qual comprimento de onda ele irradiará a maior parte da energia por unidade
de comprimento de onda? Em qual freqüência ele irradiará a
maior parte da energia por unidade de freqüência?
2.8 Suponha que a Terra fosse formada por rocha derretida a alguma
temperatura muito alta. Estime o tempo para que a Terra resfrie
até 300 K. (Nota: Este cálculo foi feito originalmente por Lord
Kelvin. O tempo de resfriamento encontrado por Kelvin foi significativamente menor do que as evidências geológicas indicavam
para a idade da Terra. Isto gerou um grande debate cientı́fico.
O problema foi resolvido com a descoberta de elementos radioativos na Terra. A energia liberada em decaimentos radioativos
aumenta o tempo de resfriamento.)
2.9 Use a lei de Stefan-Boltzmann para calcular a densidade de energia da radiação cósmica de fundo (T = 2, 74 K).
58
2 Fenômenos que deram origem à mecânica quântica
Efeito fotoelétrico
2.10 Qual é o comprimento de onda de um fóton de energia igual a
2,50 eV?
2.11 Estime a energia tı́pica de fótons de (a) um estação de rádio
FM, (b) um forno de micro-ondas (λ ≈ 0, 01 m), (c) do sol, (d)
um pedaço de cerâmica aquecida a T ≈ 1000 K e (e) dos fótons
cósmicos do universo primordial (T ≈ 3 K).
2.12 Um nı́vel de luz tı́pico para uma boa leitura corresponde a cerca
de 2 × 1013 fótons por segundo por centı́metro quadrado. Se
estes têm um comprimento de onda médio de 550 nm, qual é a
irradiância correspondente?
2.13 A corrente num experimento de efeito fotoelétrico decresce a zero
quando o potencial de retardo é aumentado para 1,25 V. Qual é
a velocidade máxima dos elétrons?
2.14 Um alvo é iluminado com luz ultravioleta de 240 nm. Elétrons
são emitidos e suas energias cinéticas variam desde próximo de
zero até 12, 0 × 10−20 J. O experimento é então refeito, desta
vez iniciando com uma luz incidente de 500 nm, e aumentando a
freqüência até que a fotocorrente comece a fluir. Determine qual
é esta freqüência inicial e o comprimento de onda correspondente.
2.15 O comprimento de onda correspondente ao limiar para que ocorra
o efeito fotoelétrico no alumı́nio é de 2.954 Å. Qual é a função
de trabalho do Al (em eV) e qual a energia cinética máxima dos
elétrons ejetados do Al por luz ultravioleta de comprimento de
onda de 1.500 Å?
2.16 A luz de uma fonte térmica (T = 6000 K) é filtrada de tal forma
que apenas fótons na região do visı́vel atingem um fotocátodo,
cuja função de trabalho é de 2,0 eV. Quando a intensidade da
luz que chega ao fotocátodo é 1 mW, uma corrente de 1 µA
é observada no circuito que detecta os fotoelétrons. Estime a
eficiência quântica do fotocátodo.
Espalhamento Compton
2.17 Um fóton de 100 MeV colide com um próton em repouso. Calcule
a perda de energia máxima que o fóton pode sofrer.
2.18 Raios X com comprimento de onda de 110 pm são espalhados por
elétrons livres a um ângulo de 20,0◦ . Encontre a variação de λ.
Exercı́cios
2.19 Relacione a direção ϕ de desvio do elétron de recuo no efeito
Compton com as freqüências ν0 e ν00 dos fótons incidentes e espalhado e o ângulo θ de espalhamento.
2.20 Um fóton de raios X de λ0 = 3 Å é espalhado por um elétron livre
em repouso, sendo desviado de 90◦ . Qual é a energia cinética de
recuo do elétron (em eV)?
2.21 Um pósitron (anti-partı́cula do elétron) de momento p~ colide com
um elétron em repouso, levando o par a aniquilar-se em dois
fótons, cujas direções de propagação formam um ângulo θ uma
com a outra. Demonstre que a soma dos comprimentos de onda
dos dois fótons é igual a λC (1 − cos θ), onde λC é o comprimento
de onda Compton do elétron.
(Dica: o cálculo é semelhante ao do efeito Compton.)
59
60
2 Fenômenos que deram origem à mecânica quântica