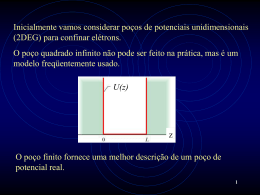
ESTABILIDADE CRÍTICA EM SISTEMAS QUÂNTICOS
Juci Melim Junior (IC)1 Tobias Frederico (PQ)2
1
Divisão de Engenharia Eletrônica, ITA, CTA, São José dos Campos, SP
e-mail: [email protected]
2
Divisão de Ensino Fundamental, ITA, CTA, São José dos Campos, SP
e-mail: tobias@…s.ita.br
RESUMO
Estudamos a forma analítica da energia de ligação de um sistema quântico de dois
corpos, para momento angular nulo, em função da profundidade do potencial, próximo
a situação crítica (energia de ligação nula). As funções obtidas para o poço quadrado,
para o potencial de Yukawa e Gaussiano podem ser caracterizadas por um expoente crítico
universal.
ABSTRACT
The analytical form of the binding energy of the quantum two-body system for zero
angular momentum is studied as a function of the potential depth near the critical condition ( zero binding energy). These functions obtained for the square-well, Yukawa and
Gaussian potentials can be characterized by a universal critical expoent .
1
INTRODUÇÃO
Neste trabalho resolvemos a equação de Schrödinger para o estado ligado de uma partícula
em uma dimensão, cuja as soluções ímpares correspondem também aos estados com momento angular nulo em três dimensões para um poço de potencial quadrado. Em seguida,
obtemos a solução numérica da equação de Schrödinger para o caso de um potencial de
Yukawa e para o caso de um potencial Gaussiano. O nosso objetivo é veri…car a universalidade do comportamento analítico da energia de ligação em função da profundidade do
potencial quando a energia de ligação tende a zero.
2
O POÇO QUADRADO
A equação de Schrödinger para o estado estacionário no caso tridimensional é dada por:
[¡
h
¹2 2
r + V (~r)]ª(~r) = Eª(~r);
2m
(1)
onde E é o autovalor do operador energia e ª(~r) é a correspondente autofunção. A
interpretação da função de onda vem através da densidade de probabilidade de encontrar
a partícula ao redor da posição ~r, que é dada por: jª(~r)j2 .
Se o estado for ligado tem-se E < 0, e o potencial, no caso do poço quadrado, é dado
por V (x) = ¡V para ¡ a2 · x · a2 , e V (x) = 0 para jxj ¸ a2 . A solução da Eq.(1) deve ser
construída separadamente já que o potencial não é contínuo. Então devemos resolvê-la
na região ¡ a2 < x < a2 e na região jxj > a2 .
O poço é simétrico em torno do zero e devido a esta simetria de re‡exão as auto-funções
são pares ou ímpares [1,2]. Assim temos para ¡ a2 < x < a2 :
u(x) = A cos k1 x;
(2)
u(x) = B sin k2 x;
(3)
como solução par e;
como solução ímpar.
Para x > a2 ocorre o tunelamento, então devemos ter uma exponencial negativa pois de
outro modo (se a exponencial fosse positiva) a probabilidade da partícula ser encontrada
no in…nito seria também in…nita e isso é …sicamente injusti…cável como pode ser veri…cado,
por exemplo, com o elétron con…nado ao orbital no átomo de hidrogênio [1,2]. Então na
região x > a2 devemos ter como solução:
(4)
u(x) = C exp(¡ke x):
Pelo mesmo motivo devemos ter uma exponencial positiva na região x < a2 , o que
garante que a probabilidade de encontrar a partícula é a mesma independentemente do
lado do poço.
2.1
Auto-funções pares
Vamos usar unidades tais que h
¹ = 1, m = 12 , e a = 2. Devemos ter a continuidade da
função de onda e de sua derivada no ponto x = a2 pois a equação diferencial para ª(x; t) é
de segunda ordem no espaço, então devemos impor a igualdade da razão entre a derivada
da função de onda e a função de onda. Isto é conhecido como a continuidade da derivada
logarítmica. Usando as funções de onda das Eqs. (2) e (4) com k1 e ke escolhidos de modo
que essas funções de onda sejam soluções da Eq. de Schrödinger para x < a=2 e x > a=2,
respectivamente, obtemos da continuidade da derivada logaritmica no ponto x = a=2, a
seguinte equação transcedental para a energia de ligação:
q
q
p
(E + V ) 2m tan (E + V ) 2m = ¡2Em:
(5)
q
Para o estado ligado E < 0 e introduzindo a variável z, dada por z = (V ¡ jEj) 2m;
p
e a variável v dada por v = 2mV
p ;temos que a equação para os autovalores da energia
de ligação reduz-se a z tan z = v 2 ¡ z 2 : Quando E = 0, temos que zn = vn e portanto a
condição crítica é dada por:
vn tan vn = 0 =) vn = n¼(n = 0; 1; 2:::);
(6)
e com isto obtemos os valores críticos da profundidade do poço para as quais a energia
de ligação é nula:
V0 = (n¼)2 (n = 0; 1; 2:::);
(7)
0,6
0,5
Energia
0,4
0,3
0,2
0,1
0,0
1,00
1,05
1,10
1,15
1,20
V/V0
Figura 1: Energia de ligação do estado par quando V está próximo a ¼ 2 . A linha
contínua é o resultado do ajuste de E como uma função quadrática de V =V n.
2.2
Auto-funções ímpares
Todo o desenvolvimento para a solução do auto-estado ímpar é análogo ao que foi feito
anteriormente para o par, de modo que, quando E = 0, temos zn = vn resultando em:
vn cot vn = 0 =) vn =
n
¼
2
(n = 0; 1; 3; 5:::);
(8)
Os valores críticos da profundidade do poço para as quais a energia de ligação é nula são,
então:
n
Vn = ( ¼)2 (n = 0; 1; 3; 5; 7:::):
(9)
2
0,06
0,05
Energia
0,04
0,03
0,02
0,01
0,00
1,00
1,05
1,10
1,15
1,20
1,25
V/V0
Figura 2: Energia de ligação do estado ímpar para V próximo a ( ¼2 )2 . Linha contínua
explicada na …gura 1.
3
OS POTENCIAIS DE YUKAWA E GAUSSIANO
Após o estudo da solução da equação de Schrödinger para o poço quadrado quando a
energia do estado ligado é próxima de zero vamos analisar na mesma situação os potenciais
de Yukawa e Gaussiano. Para resolver a equação de Schrödinger nesses casos vamos usar
métodos numéricos. Vamos transformar a equação de Schrödinger independente do tempo
da representação de coordenadas para a representação no espaço dos momentos.
A equação de Schrödinger para o estado estacionário no caso tridimensional é dada
pela Eq.(1). A transformada de Fourier da função de onda, Ã(~p), de…ne a densidade
de probabilidade de encontrar a partícula com momento p~. O elemento de matriz do
potencial na representação de momento é dada por h~p0 jV j~pi = v(j~qj2 ):
Z
2
v(j~qj ) =
d3 p
i~q:~r
V (r) exp[¡
];
3
(2¼¹h)
h
¹
(10)
onde ~q = ~p ¡ ~p0 . No caso particular dos estados com momento angular nulo, o potencial
é integrado sobre o ângulo entre ~p0 e p~:
0
0
v (p ; p) = 2¼
Z
1
¡1
dcos(µ)v(j~p0 ¡ ~pj2 ):
(11)
Desta forma chegamos a seguinte expressão para a equação de Schrödinger na representação no espaço dos momentos para um estado de momento angular nulo, cuja função
de onda depende apenas de j~pj = p:
p02
Ã(p0 ) +
2m
Z
1
0
v0 (p0 ; p)Ã(p)p2 dp = EÃ(p0 ):
(12)
Para o potencial de Yukawa, dado por
Vy (r) = ¸y
exp(¡¹r)
;
r
(13)
resulta que v(q 2 ) para este potencial é
¸0y
:
vy (q ) = 2
¹ + q2
2
(14)
Para o exemplo do potencial gaussiano, dado por
Vg (r) = ¸g exp(¡¹r2 );
(15)
¡q 2
):
2¹
(16)
temos que v(q 2 ) é
vg (q 2 ) = ¸0g exp(
4
QUADRATURA DE GAUSS-LEGENDRE
Para resolvermos numericamente a equação integral encontrada no item anterior devemos
discretizar a integral de…nida. O método usado é chamado de Quadratura de GaussLegendre e consiste em aproximar a integral de…nida por um somatório de valores da
função a ser integrada, estes valores correspondem aos n zeros do polinômio de Legendre
de grau n como se segue:
I(f ) =
Z
1
¡1
f (x)dx=
~
n
X
f (xi )di :
(17)
i=1
Como a Eq.(12) possui limites de integração como sendo [0; 1) usou-se a seguinte
mudança nos limites de integração da equação acima:
(18)
[¡1; 1] ! [0; c];
que e é dada pela seguinte mudança de variáveis:
yi = c
1 + xi
2
(19)
e, como conseqüência disto tem-se:
di
dyi = c :
(20)
2
Substituindo a integral da Eq.(12) pelo somatório correspondente usando-se os pontos
de Gauss-Legendre obtem-se:
n
X
yi2
Ã(yi ) +
v 0 (yi ; yj )Ã(yj )yj2 dyj = EÃ(yi ):
2m
j=1
(21)
Tabela I: Valores de potenciais (V0 ) para o com potencial de Yukawa (a) e Gaussiano
(b) quando a energia (E) do estado ligado é próxima de zero. Abaixo, N corresponde
ao número de pontos de Gauss- Legendre utilizado, c é a constante usada para realizar a
mudança de variável dada pela Eq.(19), ¹ é o parâmetro usado na Eq.(13) e na Eq.(15)
e Ei corresponde à energia do i-ésimo estado excitado.
N c
¹
(a) 20 10 1
(b) 20 10 1
V0
E1
E2
E3
0.84 -33.6552520 -3.08220443 -6.0436E-005
1.447 -13.6324471 -4.35246704 -9.7228E-006
1.0
Energia
0.8
0.6
0.4
0.2
0.0
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
V/V0
Figura 3: Energia referente à primeira linha da Tabela I caso (a) para o potencial de
Yukawa. Linha contínua explicada na …gura 1.
3.5
3.0
2.5
Energia
2.0
1.5
1.0
0.5
0.0
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
V/V0
Figura 4: Energia referente à primeira linha da Tabela I para o potencial Gaussiano.
Linha contínua explicada na …gura 1.
5
CONCLUSÃO
Veri…camos que, tanto para o poço quadrado como para o caso dos com potenciais
de Yukawa e Gaussiano, a energia de ligação tem o mesmo comportamento analítico
independentemente dos detalhes da interação. Isto …ca evidente quando se analisa os
resultados para a energia de ligação, para valores próximo de zero, em função da razão
da magnitude da profundidade do potencial e o seu valor crítico (para o qual a energia
de ligação é zero). A análise das …guras 1 a 4 sugere que quando a energia de ligação é
su…cientemente próxima a zero ela é proporcional a (V =Vn )2 .
AGRADECIMENTOS
Gostaria de agradecer ao Professor Tobias Frederico, meu orientador neste trabalho, por
seu estímulo, pelo seu entusiasmo e sua empolgação quando falava da física como um
todo. Por …m, gostaria de agradecer ao Professor Mauro Donizetti Tonassi, por tirar
minhas dúvidas e colaborar para que este trabalho fosse possível. Agradeço também, ao
programa PIBIC/CNPq pelo apoio …nanceiro.
REFERÊNCIAS BIBLIOGRÁFICAS
1. Beiser, A; Concepts of Modern Physics; McGraw-Hill; New York, 1967; p 01.
2. Dicke, R.H.; Wittke, J.P.; Introduction to Quantum Mechanics ; McGraw-Hill; New
York, 1970; p 01.
OBTENÇÃO DE CERÂMICA POROSA A PARTIR DA TÉCNICA DE
CONFORMAÇÃO DIRETA COM AMIDO COMERCIAL
F.A. Almeida (PG) (a), F.C.L. Melo (PQ)(b), G.P. Thim (PQ) (a)
(a) Departamento de Química - Instituto Tecnológico de Aeronáutica / ITA - CTA
(b) Divisão de Materiais / AMR – CTA
RESUMO
Cerâmicas porosas têm sido aplicadas como isolantes térmicos, filtros, membranas,
queimadores de gás, materiais para implantes ósseos, entre outros. A conformação de materiais
porosos com amido está fundamentada nas propriedades de formação de gel em água, tornando
possível seu uso como agente conformador e formador de poros. Esta técnica permite um bom
controle da porosidade do produto final, pois os poros terão o formato inicial dos grãos de amido,
considerando sua expansão no meio aquoso. As suspensões coloidais foram feitas com alumina A1000 (Alcoa Chemicals), amido de mandioca comercial em pó e defloculante. Para formação de
grandes poros na matriz cerâmica, esferas de poliestireno expandido foram adicionados às
suspensões antes da etapa de gelatinização. Após essa etapa, os corpos verdes foram submetidos a
secagem em temperatura ambiente por 96 horas e em estufa a 105ºC por 2 horas. Posteriormente
submetidos a etapa de pré-sinterização, eliminando-se os materiais voláteis e sinterizados a 1400ºC
por 2 horas. A caracterização foi feita por microscopia óptica, microscopia eletrônica de varredura
(MEV); e tiveram densidade e porosidade aparente calculadas pelo método de Arquimedes.
ABSTRACT
Porous ceramics have been used as thermal insulate, filters, membranes, gas burners and
materials for bone implants, just to mention some. The fundamental aspect of porous materials
consolidation from starch, is the property of its gelling in water. This characteristic led to use it as
solidification agent and pores producer. This technique allows a good porosity control of the
developed product, because the porous structures will be formed in the initial places of the starch
grains, considering its expansion in the aqueous medium. The colloidal suspensions were made with
alumina type A-1000 (Alcoa Chemicals), commercial cassava´s starch and dispersant. In order to
produce larger pores in the ceramics matrix, expanded polyestirene spheres were added in
suspensions before gelling step. After this step, the consolidated bodies were dried at room
temperature for 96 hours and at 105ºC for 2 hours. Then, they have been pre-sintered to burn out the
volatile materials and sintered at 1400ºC for 2 hours. Characterization was performed by optical and
scanning electron microscopy (SEM); and bulk density and apparent porosity measured by
Archimedes method.