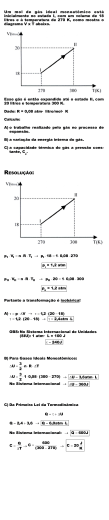
CLIQUE O MOUSE PARA NOVAS INFORMAÇÕES
OLÁ !!!
Você deve utilizar este arquivo para:
1. Rever toda a matéria através deste resumo.
2. Resolver as questões contidas no final da apresentação.
Não fique nervoso.
Faça seus exercícios e estude tranqüilo, assim
você se sairá bem nas provas.
Mas ATENÇÃO!!!
Qualquer dúvida procure o seu professor,
ESTADO GASOSO
CARACTERÍSTICAS
• movimento caótico das moléculas, que
estão em alta velocidade.
• moléculas muito pequenas, se comparadas
com a distância entre elas.
• há colisões elásticas das moléculas entre
si e com as paredes do recipiente.
VARIÁVEIS DE ESTADO
VOLUME (V)
1 cm3 = 1 mL
1 L = 1 dm3
1 L = 1000 mL
TEMPERATURA (T)
oC + 273 = K
e scala C e lsiu s
o
100 C
tc
PRESSÃO (P)
0 oC
e scala Ke lvin
373 K
T
273 K
1 atm = 760 mmHg = 760 Torr
o
-273 C
0K
TRANFORMAÇÕES GASOSAS
ISOTÉRMICA
(Lei de Boyle)
ISOBÁRICA
(Lei de Gay-Lussac)
ISOCÓRICA
(Lei de Charles)
P1.V1 = P2.V2
V1 V2

T1 T2
P1 P2

T1 T2
P
2
P2
Isoterma
P1
P
V
1
Isobárica
V2
V
2
V
Isocórica
P2
V
1
P1
V1
P1
V1
(1)
P2
V2
(2)
T1
T2
T
T1
T2
T
Em resumo...
Transformações de uma certa
massa de gás, mantém a seguinte
relação para o estado inicial (1) e
estado final (2):
P1.V1
P2.V2
=
T1
T2
obs.: deve-se sempre utilizar temperatura absoluta (em Kelvin)!
EQUAÇÃO DE CLAPEYRON
• Sabemos que as variáveis de estado de um gás mantêm uma relação
sempre constante:
P . V = constante
T
• Se n = 1 mol de gás, temos:
• Se n = 2 mol de gás, temos:
• Se temos n de gás, temos:
Logo:
PV = nRT
P . V = 0,082
T
P . V = 2 . 0,082
T
P . V = n . 0,082
T
onde P…pressão
V…volume
n … quantidade (mol) de gás
R … constante universal dos gases
T …temperatura absoluta
Qual o valor da constante universal
dos gases
R ?????
Se você utilizar a pressão em atm, use
0,082 atm.L/mol.K
Se você utilizar a pressão em mmHg, use
62,3 mmHg.L/mol.K
VOLUME MOLAR
É o volume ocupado por 1 mol de gás.
Como calcular?
PV = nRT
Considere 1 mol de gás a 0oC (273K) e pressão igual a 1 atm:
P V = nRT
1 . V = 1 . 0,082 . 273
V = 22,4 litros
PRINCÍPIO DE AVOGADRO
Volumes iguais de quaisquer gases, nas mesmas condições de
temperatura e pressão, contêm o mesmo número de moléculas
Considere os gases abaixo a 0oC (273K) e pressão igual a 1 atm:
H2
O2
CO2
22,4 L
22,4 L
22,4 L
MISTURA GASOSA
Gás A Gás B -
Ptotal = 2 atm
Na mistura há
70% do gás A,
logo a sua pressão
parcial será 70%
da pressão total:
PA = XA . Ptotal
PA = 0,7 . 2,0
PA = 1,4 atm
Na mistura há
30% do gás B,
logo a sua pressão
parcial será 30%
da pressão total:
PB = XB . Ptotal
PB = 0,3 . 2,0
PB = 0,6 atm
DIFUSÃO E EFUSÃO GASOSA
DIFUSÃO :
EFUSÃO :
distribuição espontânea de um gás em outro.
difusão de um gás através de um orifício.
Velocidade de difusão ou de efusão, nas mesmas T e P ,
dependem da massa das moléculas
-
Lei de Graham: V A

VB
MB
MA
Quanto mais leve, maior é a velocidade.
DENSIDADE
Densidade Absoluta:
d  mV
Pode-se determinar a densidade de um gás a partir da equação de Clapeyron:
m
m P. M
P.V  n. R. T  P.V 
. R. T 

M
V
R. T
P. M
Logo: d 
R. T
Densidade Relativa: é a densidade de um gás (A) em relação a outro gás (B)
P. M A
dA
MA
R
.
T
d A, B 
 d A, B 
 d A, B 
P. M B
dB
MB
R. T
M O2 32
Por exemplo: d O2 , H2 

 16
M H2
2
Exercícios
(As resoluções estão no final)
Agora que você já revisou toda a matéria, resolva as questões abaixo
colocando as resoluções em uma folha avulsa.
1. Uma certa amostra de gás encontra-se a 1520 mmHg
a uma temperatura de -73oC. Qual será sua nova temperatura, em graus Celsius, se numa transformação isocórica, sua pressão passar para 1 atm?
R: -173oC
2. Dez litros de um certo gás está sob pressão de 3atm a 27oC. Qual será
o novo volume do gás a 1atm de pressão e 127oC?
R: 40 L
3. Um extintor de incêndio contém 4,4kg de CO2.
Qual o volume máximo de gás liberado na atmosfera, a 1atm e -173oC? (C=12; O=16)
R: 820 L
4. 240 g de um certo gás Xa ocupam um volume 41 litros
à pressão de 2 atm e -73oC. Sabendo-se que a massa
atômica de X é 16u, determine o número de a.
R: a = 3
5. (FAAP) Num recipiente fechado, de volume igual
a 15 litros, está contida uma mistura constituída por
20% molar de CH4 e 80% molar de C2H6, à temperatura de 27oC e pressão de 1,64 atm. Calcule as
massas dos componentes da mistura, bem como suas
respectivas pressões parciais. Dados: C=12; H = 1
R: 3,2g de CH4 e 24g de C2H6
0,328 atm de CH4 e 1,312 atm de C2H6
6. Nas mesmas condições de P e T, um gás X atravessa um
pequeno orifício a uma velocidade três vezes menor do que
o hélio. A massa molecular do gás X é: (Dado: He = 4)
a) 30
b) 32
c) 36
d) 40
e) 44
1. P1
P2
1520 760
 

 T2  100K ou  173o C
T1 T2
200 T2
2. P .V
P2 .V2
3.10 1.V2
1 1



 V2  40l
T1
T2
300 400
3. P.V  n.R.T
P.V 
m
4400
.R.T  1.V 
.0,082.100  V  820l
M
44
4. P.V  n.R.T  P.V  m .R.T  2.41  240.0,082.200  M  48g / m ol
M
X a  48u 16a  48  a  3
M
5. P.V  n.R.T  1,64.15  n.0,082.300  n  1m ol
20% de CH 4  0,2m ol ou 3,2g
1m ol
80% de C 2 H 6  0,8m ol ou 24g
PCH 4  X CH 4 .PT  PCH 4  0,2.1,64  PCH 4  0,328atm
PC2H 6  X C2 H 6 .PT  PC2 H 6  0,8.1,64  PC2 H 6  1,312atm
6. V
X

VHe
VHe
M He
4
1
4
3


 
MX
VHe
MX
3
MX
2
1
4
 1   4 
 
 M X  36u
  

9 MX
 3  MX 
2
ESPERO QUE TENHA
APROVEITADO BEM !!!