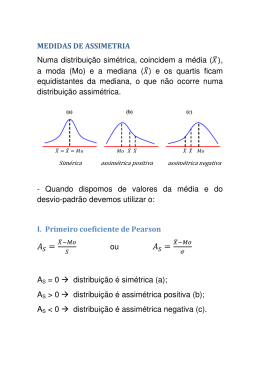
Análise de Regressão
Profa Alcione Miranda dos Santos
Departamento de Saúde Pública
UFMA
Introdução
Uma das preocupações estatísticas ao analisar dados, é
a de criar modelos que explicitem estruturas do fenômeno
em observação.
O modelo de regressão é um dos métodos estatísticos
mais usados para investigar a relação entre variáveis.
Análise de regressão: metodologia estatística que
estuda (modela) a relação entre duas ou mais variáveis.
Tipos de Modelos de Regressão
Uma variável
dependente
Modelo
Regressão
Multiplo
Multíplo
Simples
Linear
Duas ou mais variáveis
dependentes
Não
Linear
Linear
Não
Linear
A presença ou ausência de relação linear pode
ser investigada sob dois pontos de vista:
Quantificando a força dessa relação:
correlação.
Explicitando a forma dessa relação:
regressão.
Coeficiente de Correlação de Pearson
A correlação é calculada independente da unidade de medida das
variáveis.
A técnica usada para calcular este coeficiente, supõe que a associação
entre as variáveis seja linear, ou seja, expressa por uma reta ou linha.
Se a relação apresentada no diagrama de dispersão não for do tipo
linear, o coeficiente de correlação de Pearson não deve ser calculado.
Fórmula:
n
∑ ( x − x)( y
i
r=
i
− y)
i =1
n
n
i =1
i =1
2
2
(
x
−
x
)
×
(
y
−
y
)
∑ i
∑ i
Coeficiente de correlação de Pearson
O coeficiente de correlação pode variar entre –1
(correlação negativa perfeita) e +1 (correlação positiva
perfeita).
Valores negativos do coeficiente de correlação indicam
uma correlação do tipo inversa, isto é, quando x
aumenta y diminui.
Valores positivos do coeficiente de correlação ocorrem
quando x e y variam no mesmo sentido, isto é, quando x
aumenta y aumenta ou quando x diminui y também
diminui.
Exemplo 1: Um psicólogo está investigando a relação entre o tempo que
um indivíduo leva para reagir a um estímulo visual (Y) com o sexo (W), idade
(X) e acuidade visual (Z, medida em porcentagem).
X : idade
Y : tempo de reação
130
120
⇓
110
Modelo de regressão
Y
Pelo gráfico: média de Y aumenta
conforme as pessoas envelhecem
100
90
20
30
40
X
Correlação entre Y e X = 0,7681
Correlação no STATA
Comando: corr y x
Para o exemplo anterior, temos
corr tempo idade
(obs=20)
|
tempo
idade
-------------+-----------------tempo |
1.0000
idade |
0.7681
1.0000
Diagramas de dispersão
Comando STATA: scatter y x
Modelo de regressão linear simples
yi = β0 + β1xi +ei ,
i=1,...,n
sendo
yi: valor da variável dependente (resposta) para o i-ésimo elemento da
amostra;
xi: valor (conhecido) da variável independente ou preditora para o i-ésimo
elemento da amostra;
β0 e β1 são parâmetros desconhecidos;
ei: erro amostral.
Suposição: os erros amostrais são independentes com distribuição N(0, σ2), i=1,2,...,n.
Esta suposição deve ser verificada!!! (como??)
Modelo de regressão linear simples
Amostra Aleatória
População
Yi = β 0 + β 1 X i + ε i
☺$
☺$
☺$
☺$
Y ii = β$ 00 + β$ 11X ii + ε$ ii
☺$
Erro amostral
O erro amostral é uma variável aleatória não observável, e é
estimado pelos resíduos, isto é, a diferença entre o valor observado
Y, e o estimado pela reta Ŷ , isto é
n
∑
i =1
n
^
εˆi =∑ (Y − Y ) 2
2
i
i =1
i
Estimação dos parâmetros
Qual modelo de regressão deve ser ajustado?
60
40
20
0
Y
0
20
40
X
60
Estimação dos parâmetros
Método de mínimos quadrados
Objetivo: minimizar a soma dos quadrados dos erros
SQ(β0, β1)= Σ(yi- Yˆi )2
= Σ(yi- β0 - β1xi)2
Para que a soma dos quadrados dos erros tenha um valor mínimo, devem-se aplicar
os conceitos de cálculo diferencial com derivadas parciais.
Portanto, os estimadores dos parâmetros são:
n
βˆ1 =
∑
xi yi − nx y
i =1
n
∑
=
2
i
x − nx
2
SS
xy
SS
xx
i =1
βˆ 0 = y − βˆ1 x
Reta ajustada:
yˆ i = βˆ0 + βˆ1 xi
Interpretação dos parâmetros
Intercepto β0 - valor esperado para a variável
dependente yi quando xi é igual a zero
Coeficiente angular β1 - variação esperada na
variável resposta, quando a variável
independente aumenta uma unidade.
Exemplo 1:
Um psicólogo está investigando a relação entre o tempo que o
indivíduo leva para reagir a um certo estimulo (em segundos) e algumas de suas
características tais como sexo, idade (em anos completos) e acuidade visual
(medida em porcentagem). O resultado de 20 indivíduos estão mostrado na tabela
abaixo (Adaptado de Bussab, 1986).
i
tempo
sexo
idade
acuidade
i
tempo
sexo
idade
acuidade
1
96
M
20
90
11
109
M
30
90
2
92
F
20
100
12
100
F
30
80
3
106
M
20
80
13
112
F
35
90
4
100
F
20
90
14
105
F
35
80
5
98
F
25
100
15
118
M
35
70
6
104
M
25
90
16
108
M
35
90
7
110
M
25
80
17
113
F
40
90
8
101
F
25
90
18
112
F
40
90
9
116
F
30
70
19
127
M
40
60
10
106
M
30
90
20
117
M
40
80
1.Tempo de reação ⇒ variável dependente ou resposta
idade ⇒ variável independente
⇓
modelo de regressão linear simples
2. Tempo de reação ⇒ variável dependente ou resposta
sexo, idade, acuidade visual ⇒ var. independentes
⇓
modelo de regressão linear múltipla
Primeiramente, vamos considerar um modelo de regressão linear
simples, sendo X : idade e Y : tempo de reação
90
100
Tempo
110
120
130
20
25
30
idade
35
Dados: n=20, Σyi= 2150, Σxi=600, Σxiyi=65400, Σxi2=19000
40
Estimação dos parâmetros:
65400 − 20.30.107,5
ˆ
β1 =
= 0,90
2
19000 − 20.30
βˆ0 = 107,50 − 0,90.30 = 80,50
Reta ajustada:
yˆ i = 80,50 + 0,90 xi
Interpretação β̂1 : Para um aumento de 1 ano na
idade, o tempo médio de reação aumenta 0,90.
Dada a reta ajustada, podemos prever, por
exemplo, o tempo médio de reação para pessoas
de 20 anos
Valor predito
ŷ ( 20) = 80,50 + 0,90.20 = 98,50
Vantagem: permite estimar o tempo médio de reação para idades não
observadas
Valor predito
ŷ ( 33 ) = 80 ,50 + 0,90 .33 = 110 , 20
NOTA: A estimativa pode ser melhorada com a construção de intervalos de confiança
Análise de Variância para o MRLS
No desenvolvimento de um teste ANOVA, considere a definição de
três tipos de resíduos, ou fontes de variação, expressos pelas
seguintes Somas dos Quadrados (SQ):
TOTAL cuja soma dos quadrados é dada por:
_
SQT = Σ(Y − Y ) 2
RESÍDUOS com a soma dos quadrados expressa através de:
SQE = Σ(Y − Yˆ ) 2 = Σ(Y − βˆ0 − βˆ1 X ) 2 = Σe 2
MODELO, resultante das distâncias entre os valores do modelo e a média:
_
_
SQR = Σ(Y − Y ) − Σ(Y − Yˆ ) =Σ(Yˆ −Y ) 2
2
2
A tabela ANOVA para o MRLS é definida de acordo com o que se
apresenta em seguida.
Fontes de
Variação
Regressão
Resíduo
Total
g.l.
1
n-2
n-1
SQ
SQM
F
SQR
SQR
1
SQR
SQE/(n-2)
SQE
SQE
n-2
SQT
SQT
n-1
Regressão Linear Simples no STATA
Comando: regress y x1
No exemplo anterior, temos
regress tempo idade
SQR
Source |
SS
df
MS
-------------+-----------------------------Model |
810
1
810
Residual |
563
18 31.2777778
-------------+-----------------------------Total |
1373
19 72.2631579
Number of obs
F( 1,
18)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
20
25.90
0.0001
0.5899
0.5672
5.5927
SQE
-----------------------------------------------------------------------------tempo |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------idade |
.9
.1768552
5.09
0.000
.5284409
1.271559
_cons |
80.5
5.451045
14.77
0.000
69.04778
91.95222
------------------------------------------------------------------------------
β0
β1
Após executado o comando regress, os valores preditos podem ser
obtidos usando o comando predict. Por exemplo,
regress tempo idade
predict yest
label var yest “valores preditos tempo“
list yest
Regressão Linear Múltipla
A análise de uma regressão múltipla segue, basicamente, os mesmos critérios
da análise de uma regressão simples.
Vamos supor que temos X1, X2,..., Xp-1 variáveis preditoras. Definamos modelo
de regressão multíplo, em termos das variáveis preditoras:
Yi = β 0 + β1 X i1 + β 2 X i 2 + ... + β p −1 X i , p −1 + ε i
Sendo:
β0, β1,..., βp-1, parâmetros desconhecidos;
εi erro amostral
Suposição: os erros amostrais são independentes com distribuição N(0, σ2), i=1,2,...,n.
Exemplo 2:
Considere novamente o exemplo 1. Vamos agora,
trabalhar com as seguintes variáveis:
X1: idade
X2: sexo
X3: acuidade Y: tempo
Assim, o modelo de regressão linear múltiplo será dado por
Yi = β 0 + β1 X i1 + β 2 X i 2 + β 3 X i ,3 + ε i
Observe que, agora dispomos de variáveis quantitativas e qualitativas no
modelo.
Uma ferramenta útil no processo de escolha preliminar das possíveis variáveis
explicativas que deverão entrar no modelo é a matriz de correlação entre as
variáveis quantitativas.
Para nosso exemplo, temos a seguinte matriz de correlação:
pwcorr tempo idade acuidade, sig
|
tempo
idade acuidade
-------------+--------------------------tempo |
1.0000
|
|
idade |
0.7681
1.0000
|
0.0001
|
acuidade | -0.7553 -0.3990
1.0000
|
0.0001
0.0814
|
Ajustando o modelo de regressão com estas variáveis, temos:
regress tempo idade sexo acuidade
Source |
SS
df
MS
-------------+-----------------------------Model | 1173.60282
3 391.200941
Residual | 199.397178
16 12.4623236
-------------+-----------------------------Total |
1373
19 72.2631579
Number of obs
F( 3,
16)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
20
31.39
0.0000
0.8548
0.8275
3.5302
-----------------------------------------------------------------------------tempo |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------idade |
.679224
.1229709
5.52
0.000
.4185374
.9399106
sexo | -2.791534
1.675998
-1.67
0.115
-6.344491
.7614219
acuidade | -.4014109
.0937644
-4.28
0.001
-.6001826
-.2026393
_cons |
125.4305
9.626618
13.03
0.000
105.023
145.838
------------------------------------------------------------------------------
Reta ajustada:
Yi = 125,43 + 0,68 X i1 − 2,79 X i 2 − 0,40 X i ,3
Também podem ser calculados os valores preditos:
regress tempo idade sexo acuidade
predict yest
label var yest “valores preditos tempo“
list yest
Avaliação do Modelo
Algumas avaliações devem ser realizadas para se ter alguma idéia da
eficácia e adequação do modelo.
Dentre as técnicas utilizadas para avaliar a eficácia do modelo, o
coeficiente de correlação seria uma primeira possibilidade.
Outra medida de adequação é o coeficiente de determinação do
modelo.
A determinação do “melhor” modelo, ou do modelo que melhor se
ajusta aos dados, está relacionada com a estimativa dos parâmetros
que tornem os resíduos tão próximos de zero quanto possível.
Deve-se então, testar a significância estatística dos parâmetros do
modelo.
Avaliando a significância do parâmetro
Hipóteses:
H 0 : βk = 0
H a : βk ≠ 0
Estatística de teste:
tcal =
βk
s(βk )
Critério do teste:
Se |tcal| ≤ t(1-α/2;n-p), aceita-se a hipótese nula, caso contrário rejeita-se a
mesma.
Nota: Quando não dispomos da tabela t-student, podemos utilizar o p-valor,
fornecido por vários programas estatísticos. Se p-valor menor que o nível de
significância, rejeitamos H0.
Considere o modelo de regressão múltipla ajustado anteriormente:
Yi = 125,43 + 0,68 X i1 − 2,79 X i 2 − 0,40 X i ,3
Para determinarmos quais parâmetros são estatisticamente significantes,
basta observar o p-valor fornecido na tabela ANOVA.
regress tempo idade sexo acuidade
Source |
SS
df
MS
-------------+-----------------------------Model | 1173.60282
3 391.200941
Residual | 199.397178
16 12.4623236
-------------+-----------------------------Total |
1373
19 72.2631579
Number of obs
F( 3,
16)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
20
31.39
0.0000
0.8548
0.8275
3.5302
-----------------------------------------------------------------------------tempo |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------idade |
.679224
.1229709
5.52
0.000
.4185374
.9399106
sexo | -2.791534
1.675998
-1.67
0.115
-6.344491
.7614219
acuidade | -.4014109
.0937644
-4.28
0.001
-.6001826
-.2026393
_cons |
125.4305
9.626618
13.03
0.000
105.023
145.838
------------------------------------------------------------------------------
Apenas a variável sexo não é estatisticamente significante, considerando
um nível de significância de 5%.
Coeficiente de Determinação
Ao se analisar a reta de regressão
observamos que os pontos (xi, yi)
estão distribuídos acima e abaixo da
mesma.
O coeficiente de determinação deve
ser interpretado como a proporção de
variação total da variável dependente
que é explicada pela variação da
variável independente X.
O coeficiente de determinação, no
caso univariado, é igual ao quadrado
do coeficiente de correlação.
Coeficiente de determinação
nn
Observe que o coeficiente de
determinação é sempre positivo,
enquanto que o coeficiente de
correlação pode admitir valores
negativos e positivos.
22
rr ==
nn
∑ (YY −−YY ) −−∑ (YY −−YYˆˆ)
22
22
ii
ii
ii==11
ii==11
nn
∑ (YY −−YY )
22
ii
ii==11
==
SQE
SQE
SQT
SQT
Coeficiente de Determinação no STATA
No exemplo 1, temos
regress tempo idade
Source |
SS
df
MS
-------------+-----------------------------Model |
810
1
810
Residual |
563
18 31.2777778
-------------+-----------------------------Total |
1373
19 72.2631579
Number of obs =
F( 1,
18) =
Prob > F
=
R-squared
20
25.90
0.0001
=
Adj R-squared =
Root MSE
=
0.5899
0.5672
5.5927
-----------------------------------------------------------------------------tempo |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------idade |
.9
.1768552
5.09
0.000
.5284409
1.271559
_cons |
80.5
5.451045
14.77
0.000
69.04778
91.95222
------------------------------------------------------------------------------
R2 x 100 = 59% ( porcentagem de variância explicada pelo modelo).
Coeficiente de Determinação no STATA
No exemplo 2, temos
regress tempo idade sexo acuidade
Source |
SS
df
MS
-------------+-----------------------------Model | 1173.60282
3 391.200941
Residual | 199.397178
16 12.4623236
-------------+-----------------------------Total |
1373
19 72.2631579
Number of obs =
F( 3,
16) =
Prob > F
=
20
31.39
0.0000
R-squared
=
Adj R-squared =
Root MSE
=
0.8275
3.5302
0.8548
-----------------------------------------------------------------------------tempo |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------idade |
.679224
.1229709
5.52
0.000
.4185374
.9399106
sexo | -2.791534
1.675998
-1.67
0.115
-6.344491
.7614219
acuidade | -.4014109
.0937644
-4.28
0.001
-.6001826
-.2026393
_cons |
125.4305
9.626618
13.03
0.000
105.023
145.838
------------------------------------------------------------------------------