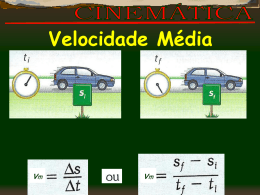
Cinemática: Conceitos Básicos
Ponto Material e Localização
Em cinemática, estudamos o movimento de um corpo qualquer, que pode ser um homem, um animal, um
planeta, um meio de transporte, etc. Chamamos esse corpo genericamente de móvel. Na maioria dos casos, os
móveis podem ser considerados pontos materiais, ou seja, suas dimensões podem ser desprezadas quando
comparadas com as distâncias envolvidas no fenômeno.
Um exemplo seria quando viajamos 80 km num ônibus com 10 m de comprimento, sentados no último
banco. Neste caso, não levamos em conta o tamanho do ônibus (10 m) em relação à distância percorrida por ele.
O comprimento do ônibus (10 m) é desprezível em comparação com a distância percorrida (80 km). Nestas
condições, o ônibus pode ser considerado um ponto material.
Suponhamos agora que o mesmo ônibus esteja manobrando para sair ou entrar numa garagem. Nesse
caso, o veículo não pode ser considerado ponto material, pois o seu comprimento não pode ser desprezado em
relação às dimensões da garagem.
No estudo de um movimento, nosso principal objetivo é a localização do móvel em qualquer instante.
Por exemplo, para socorrer uma pessoa cujo carro tenha sofrido avaria durante uma viagem, precisamos
saber onde ela está com seu veículo. Para isso, a pessoa deve nos fornecer a sua posição em relação a algum
ponto da estrada que nos sirva de “referência”. Ou seja, precisamos de um referencial.
Movimento e Repouso
Podemos dizer que um corpo se encontra em movimento quando sua posição muda no decorrer do
tempo. Se, durante um intervalo de tempo, ele mantém sua posição constante, dizemos que ele se encontra em
repouso.
Tais condições não invalidam a possibilidade de um móvel estar em movimento em relação a um
observador e, ao mesmo tempo, em repouso em relação a outro observador. Um exemplo seria você sentado
numa sala de aula lendo um livro. Você estará em repouso em relação ao solo, mas em movimento em relação ao
seu professor, caso ele estiver andando pela sala.
É necessário esclarecer que, durante uma aula, o seu professor se movimenta em relação a você, mas, em
relação a ele, é você que se movimenta. Portanto, podemos concluir que o movimento é sempre relativo: ele
existe em relação a um determinado referencial.
Um corpo em movimento ocupa uma determinada posição num certo instante de tempo. Unindo uma a
uma as sucessivas posições por ele ocupadas, obtemos uma linha, reta ou curva, que é justamente a trajetória
descrita pelo móvel.
A trajetória de um móvel depende do referencial escolhido. Diferentes observadores podem descrever
um mesmo movimento de maneiras diferentes. Por exemplo, um patinador, deslocando-se com velocidade
“constante”, lança uma bola verticalmente para cima, apanhando-a um pouco adiante. A trajetória da bola é um
arco de parábola, para um observador que esteja sentado, assistindo a apresentação do patinador. Mas para o
patinador a trajetória da bola é uma reta vertical, porque a bola sobe e desce, caindo sempre em sua mão.
Deslocamento (∆s) e Distância ( ∆s )
Localizar um objeto significa determinar sua posição relativa a um ponto de referência, em geral, a
origem (ou ponto zero) de um eixo, como o eixo s na figura abaixo. O sentido positivo do eixo é crescente na
escala numérica “em geral”, ou seja, da esquerda para a direita. O sentido negativo é o oposto.
1
Uma partícula pode, por exemplo, estar localizada em s = 5 m, significando que está a 5 m da origem, no
sentido positivo. Se fosse em s = −5 m, estaria, igualmente, afastada 5 m da origem, mas no sentido oposto.
A variação de uma posição inicial so para uma posição final sf chama-se deslocamento.
∆s = s f − s o
⇒
deslocamento
O símbolo ∆, que representa a variação de uma grandeza, significa que o valor inicial da grandeza deve
ser subtraído do valor final. Quando consideramos valores, um deslocamento no sentido positivo é um número
positivo e no sentido contrário é negativo. Chama-se a atenção aqui que a equação mostrada acima “não é geral”,
isto é, não é válida para todos os casos. A mesma funciona muito bem apenas para trajetórias retilíneas. Sendo
assim, a definição mais precisa para o deslocamento é:
O deslocamento é a distância, medida em “linha reta”, que liga a posição inicial à posição final do móvel.
Mais adiante, nos exemplos, serão tratados alguns casos envolvendo trajetórias retilíneas e curvas para cálculo
do deslocamento.
O módulo, ou valor absoluto (simbolizado entre barras), do deslocamento representa a distância da
posição inicial à posição final do móvel, sempre medida ao longo da trajetória.
∆s
⇒
distância
O cálculo da distância depende muito da “forma” da trajetória seguida pelo móvel. Mais adiante, nos
exemplos, serão tratados alguns casos envolvendo trajetórias retilíneas e curvas para cálculo da distância.
O deslocamento pode ou não coincidir com a distância efetivamente percorrida pelo móvel. O
deslocamento e a distância são iguais, em módulo, quando não há inversão no sentido do movimento realizado
ao longo de uma trajetória retilínea.
Velocidade Média (vm)
A velocidade média vm é a razão entre o deslocamento efetuado por um móvel pelo intervalo de tempo
em que ocorreu este evento. Em outras palavras, a velocidade é a taxa de variação da posição com o tempo.
vm =
∆s
∆t
⇒
velocidade média
Velocidade Escalar Média ( vm )
A velocidade escalar média vm é uma forma diferente de descrever a “rapidez” de um móvel. Enquanto
a velocidade média é uma função do deslocamento ∆s do móvel, a velocidade escalar média é função da
distância total ∆s percorrida (por exemplo, o número de metros), independentemente do sentido.
vm =
∆s
∆t
⇒
velocidade escalar média
No SI, a unidade para velocidade é o metro por segundo (m/s), mas uma unidade muito utilizada na
prática é o quilômetro por hora (km/h).
Para transformar de m/s para km/h, multiplicamos o valor expresso em m/s por 3,6 e, para transformar
de km/h para m/s, dividimos o valor expresso em km/h por 3,6.
2
Aceleração Média (am)
Quando a velocidade de um móvel varia, dizemos que ela está sob uma aceleração (ou está acelerada).
Em outras palavras, a aceleração é a taxa de variação da velocidade instantânea do móvel com o tempo. A
aceleração média am em um intervalo de tempo ∆t é:
am =
∆v
∆t
⇒
aceleração média
A velocidade instantânea é importante quando necessitamos de informações a respeito do
comportamento da velocidade durante um movimento. Ela pode ou não coincidir com a velocidade média.
Enquanto a primeira nos informa a velocidade em cada instante, a segunda relaciona o deslocamento total
efetuado pelo móvel com o correspondente intervalo de tempo.
No SI, a unidade da aceleração é o metro por segundo por segundo ou, como é amplamente conhecida,
metro por segundo quadrado (m/s2). Em alguns casos, a aceleração pode ser expressa em quilômetros por
hora quadrada (km/h2 ), mas não é muito freqüente.
Para transformar de m/s2 para km/h2, multiplicamos o valor expresso em m/s2 por 12.960 e, para
transformar de km/h2 em m/s2, dividimos o valor expresso em km/h2 por 12.960.
Exemplos:
1. A distância média da Terra ao Sol é cerca de 11800 vezes o diâmetro terrestre. Então, a Terra pode ser
considerada um ponto material em seu movimento de translação ao redor do Sol? Justifique.
2. Considere um homem chamado Albert, o qual está sentado num ônibus em movimento e observando
uma lâmpada fixa no teto do ônibus. Albert diz: “A lâmpada está se movimentando, uma vez que o
ônibus está em movimento”. Verifique a validade dessa afirmativa.
3. Um parafuso se desprende do teto de um ônibus que está se movimentando com velocidade constante
em relação à Terra. Desprezando a resistência do ar, descreva como seria a trajetória do parafuso, em
relação à um observador, sentado dentro do ônibus, que estivesse vendo o parafuso cair.
4. Com base no enunciado do exercício anterior, determine como seria a trajetória do parafuso visto por um
observador parado e fora do ônibus, vendo-o passar.
5. Suponha que a distância, seguida em linha reta, entre dois semáforos quaisquer seja de 600 m. Brian, um
motorista de táxi, percorreu esse trecho em 40 s. Poderia Brian então ter percorrido esse trecho com uma
velocidade média de 54 km/h? Justifique sua resposta.
6. Um carro fez uma viagem entre duas cidades, A e B, em duas etapas. A primeira metade da viagem
transcorreu a uma velocidade média de 100 km/h e a segunda metade a uma velocidade média de
80 km/h. Qual foi velocidade média de todo o trajeto?
7. Partindo do repouso, um avião percorre a pista e atinge a velocidade de 360 km/h em 25 s. Qual é o
valor da aceleração média em m/s2?
3
8. Dois móveis, 1 e 2, partem simultaneamente do repouso no ponto
A e seguem em direção ao ponto B, mostrado na figura ao lado. O
móvel 1 segue a trajetória curva que equivale a um quarto de uma
circunferência cujo raio, que corresponde à distância entre A e P
(sendo esta igual à distância entre P e B obviamente), vale
100 km. Já o móvel 2 segue até B passando por P. Ambos
chegam juntos ao ponto B, após 1h40min da partida em A. O
móvel 1 chega em B com uma velocidade de 600 m/s e o móvel 2
com velocidade de 580 m/s. Sendo assim, determine:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
A distância percorrida pelo móvel 1 entre os pontos A e B.
A distância percorrida pelo móvel 2 entre os pontos A e B.
O deslocamento efetuado pelo móvel 1 entre os pontos A e B.
O deslocamento efetuado pelo móvel 2 entre os pontos A e B.
A velocidade média do móvel 1 entre os pontos A e B em km/h.
A velocidade média do móvel 2 entre os pontos A e B em km/h.
A velocidade escalar média do móvel 1 entre os pontos A e B em km/h.
A velocidade escalar média do móvel 2 entre os pontos A e B em km/h.
A aceleração média do móvel 1 entre os pontos A e B em m/s2.
A aceleração média do móvel 2 entre os pontos A e B em m/s2.
Informações úteis para os exercícios propostos:
Teorema de
Pitágoras:
r = a2 + b2
Circunferência (C) do
Círculo de raio r:
C = 2 ⋅π ⋅ r
onde
π = 3,14
Exercícios Propostos
1. “Um carro em uma estrada, fazendo uma viagem, pode ser considerado um ponto material”. Verifique a
validade dessa afirmativa.
2. Você recebe a mensagem de um amigo dizendo que às 12h ele se encontrava no km 250 da rodovia
Belém−Brasília. A partir dessa informação é possível para você:
a) Fornecer a localização do seu amigo?
b) Dizer para onde ele se dirigia?
c) Determinar quantos quilômetros ele havia percorrido?
3. Um homem está parado no degrau de uma escada rolante em movimento. Assinale a alternativa correta.
a)
b)
c)
d)
e)
O movimento do homem e da escada são diferentes.
Para um referencial no solo, o homem não está em movimento.
Para um referencial na escada, o homem está em movimento.
Para um referencial no solo, a escada não está em movimento.
O homem está em repouso em relação à escada.
4
4. Um homem, em pé sobre a carroceria de um caminhão que se move em uma estrada com velocidade
constante, lança uma pedra verticalmente para cima. Com relação ao movimento da pedra e
desprezando-se a resistência do ar, é correto afirmar que:
a)
b)
c)
d)
e)
Ela cairá no chão, atrás do caminhão, se a velocidade deste for grande.
Ela cairá nas mãos do homem, qualquer que seja a velocidade do caminhão.
Em relação à estrada, a pedra tem movimento retilíneo.
Em relação ao caminhão, o movimento da pedra é curvilíneo.
Em relação ao homem, a trajetória da pedra é um arco de parábola.
5. Um móvel se desloca de A para D e, em seguida, retorna ao ponto B, conforme a figura. Determine:
a)
b)
c)
d)
O deslocamento realizado de A para D.
A distância percorrida de A para D.
O deslocamento realizado de A → D → B (isto é: parte de A, vai até D e pára em B).
A distância percorrida de A → D → B.
6. Com base no exercício 5, se o móvel se desloca de A para D e, em seguida, retorna ao ponto A:
a) Qual será o deslocamento realizado de A → D → A.
b) A distância percorrida de A → D → A.
7. Um móvel parte do repouso no ponto A e segue em direção ao ponto
B, mostrado na figura ao lado. A distância entre A e P vale 3 km
enquanto que a distância entre os pontos P e B mede 4 km. Sendo
assim, determine:
a) A distância percorrida pelo móvel entre os pontos A e B.
b) O deslocamento efetuado pelo móvel entre os pontos A e B.
8. Na figura abaixo, X e Y são pontos diametralmente opostos de uma circunferência. Considere duas
partículas, A e B, que partem simultaneamente de X, atingem Y e retornam a X, sendo que A caminha
sobre a circunferência, sempre no mesmo sentido, e B sobre o diâmetro XY. Determine:
a) O deslocamento da partícula A do
início ao fim do movimento.
b) O deslocamento da partícula B do
início ao fim do movimento.
c) A distância percorrida pela
partícula A durante todo o percurso.
d) A distância percorrida pela
partícula B durante todo o percurso.
9. A velocidade escalar constante da luz no vácuo vale 3×108 m/s. Expresse seu valor em km/h.
10. Um automóvel faz um percurso de 6 h, sempre no mesmo sentido. Nas duas primeiras horas, ele
percorre 100 km e, nas quatro últimas horas, percorre 140 km. Calcule a velocidade média do automóvel
no percurso todo.
5
11. Um carro percorreu 1 km com velocidade média de 40 km/h e o quilômetro seguinte com velocidade
média de 60 km/h. Qual foi a velocidade média no trajeto todo, em quilômetros por hora?
12. Uma equipe de remadores, ao disputar uma prova de 1000 m, realizou a primeira terça parte do concurso
usando a metade do tempo total gasto na prova. O tempo total da prova foi de seis minutos. Assim:
a) Qual foi a velocidade média na terça parte inicial do percurso, em quilômetros por hora?
b) Qual foi a velocidade média no restante do percurso, em quilômetros por hora?
13. Uma moto faz a primeira metade de um percurso com velocidade média de 70 km/h, e a segunda metade
com velocidade média de 50 km/h. Determine a velocidade média da moto no percurso todo.
14. Um motorista pretende percorrer uma distância de 200 km em 2,5 h. Por dificuldades no tráfego, ele teve
de percorrer 25 km à razão de 60 km/h e 20 km à razão de 50 km/h. Que velocidade média ele deve
imprimir ao veículo no trecho restante para chegar no tempo previsto.
15. Diante de uma agência do Inamps há uma fila de, aproximadamente, 100 m de comprimento, ao longo
da qual se distribuem, de maneira uniforme, duzentas pessoas. Aberta a porta, as pessoas entram durante
30 s com uma velocidade média de 1 m/s. Sendo assim, pede-se para determinar:
a) O número de pessoas que entraram na agência.
b) O comprimento da fila que restou do lado de fora.
16. Uma pessoa viaja de automóvel de Santa Maria a Porto Alegre. Ela parte de Santa Maria às 14:00, pára
às 15:30 para colocar gasolina no automóvel, demorando 10 min no posto; segue viagem até às 16:50 e
pára mais 15 min para tomar café; segue, então, mais 1h15min e chega, enfim, a Porto Alegre. Sabendo
que a distância percorrida foi de 315 km, determine a velocidade média do automóvel, em km/h.
17. Dois móveis, 1 e 2, partem simultaneamente do repouso em A, mostrado na figura abaixo. O móvel 1
segue a trajetória I, e o móvel 2 a trajetória II, chegando juntos ao ponto B após 10 s da partida em A.
Sendo assim, determine:
a)
b)
c)
d)
A velocidade média do móvel 1.
A velocidade média do móvel 2.
A velocidade escalar média do móvel 1.
A velocidade escalar média do móvel 2.
18. Ao fazer uma viagem de carro entre duas cidades, um motorista observou que sua velocidade média foi
de 70 km/h, e que, em média, seu carro consumiu 1 L de gasolina a cada 10 km. Se durante a viagem o
motorista gastou 35 L de gasolina, quantas horas demorou a viagem entre as duas cidades?
19. A velocidade de um carro aumenta de 36 km/h para 108 km/h em 5 s. Calcule a aceleração média
produzida pelo motor do carro, em m/s2.
20. Um rapaz dirige uma moto a uma velocidade de 72 km/h quando aciona os freios e pára em um doze
avos de minuto (1/12 min). Calcule a desaceleração média da moto, em m/s2.
21. Um móvel percorre a trajetória mostrada na figura abaixo no sentido de A para D. O móvel cruza o
ponto A, com uma velocidade de 90 km/h, às 11h45min e percorre uma trajetória retilínea com extensão
de 30 km até o ponto B. Aí ele segue uma trajetória curva até o ponto C que equivale a um quarto de
uma circunferência cujo raio R mede 10 km. Ao passar por C ele percorre novamente uma trajetória
retilínea, porém agora com extensão de 20 km, até cruzar o ponto D, com uma velocidade de 180 km/h,
6
às 12h15min. Sabe-se que o móvel consumiu quatro litros (4 L) de gasolina durante todo o percurso.
Com base nestes dados, determine:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)
O deslocamento efetuado pelo móvel entre os pontos A e B.
A distância percorrida pelo móvel entre os pontos A e B.
O deslocamento efetuado pelo móvel entre os pontos B e C.
A distância percorrida pelo móvel entre os pontos B e C.
O deslocamento efetuado pelo móvel entre os pontos C e D.
A distância percorrida pelo móvel entre os pontos C e D.
O deslocamento efetuado pelo móvel entre os pontos A e D.
A distância percorrida pelo móvel entre os pontos A e D.
A velocidade média do móvel entre os pontos A e D em km/h.
A velocidade escalar média do móvel entre os pontos A e D em km/h.
A aceleração média do móvel entre os pontos A e D em m/s2.
A aceleração média do móvel entre os pontos A e D em km/h2.
Qual foi o consumo médio de combustível, em quilômetros por litro (km/L), para todo o percurso?
Neste caso, use Cm = ∆s / ∆V , onde Cm é o consumo médio, ∆s é o deslocamento efetuado pelo
móvel e ∆V é a quantidade de volume de combustível consumido pelo móvel em seu deslocamento.
n) Qual o custo médio em reais (R$) para percorrer toda a trajetória se o preço da gasolina custa
R$2,60/L? Neste caso, pode-se usar Custo = ∆V (taxa ) , onde Custo é o custo médio, ∆V é a
quantidade de volume de combustível consumido pelo móvel em seu deslocamento e taxa é o valor
cobrado por quantidade de volume de combustível consumido.
o) Qual seria o custo médio em dólares (US$) para percorrer toda a trajetória, sabendo que o dólar
comercial equivale a R$2,14 (supondo que esta seja a cotação do dia)?
Respostas:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Sim, pois as dimensões da estrada são muito maiores que a do carro.
a) Sim, pois há referencial do local no qual o amigo se encontra; b) Não; c) Não.
e.
b.
a) 250 km; b) 250 km; c) 70 km; d) 430 km.
a) zero; b) 500 km
a) 7 km; b) 5 km.
a) zero; b) zero; c) 125,6 m; d) 40 m.
1,08×109 km/h.
40 km/h.
48 km/h.
7
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
a) 6,67 km/h; b) 13,33 km/h.
58,33 km/h.
92,1 km/h.
a) 60 pessoas; b) 70 m.
72,69 km/h.
a) 2 m/s; b) 2 m/s; c) 3,14 m/s; d) 2 m/s.
5 h.
4 m/s2.
−4 m/s2.
a) 30 km; b) 30 km; c) 14,14 km; d) 15,7 km; e) 20 km; f) 20 km; g) 50 km; h) 65,7 km; i) 100 km/h;
j) 131,4 km/h; k) 1,39×10−2 m/s2; l) 180 km/h2; m) 12,5 km/L; n) R$ 10,40; o) US$ 4,86.
8