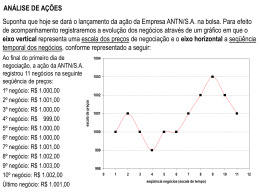
Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
1
Exercício Exemplo de Análise Matricial de Estruturas
Dada a estrutura abaixo, determine os deslocamentos no nó 2 e as reações de apoio
utilizando a análise matricial de estruturas.
Dados da Barra 1:
EA = 300000 kN
EI = 32400 kN.m²
Comprimento = 4,0 m
3
50 kN
2
2
Dados da Barra 2:
EA = 300000 kN
EI = 32400 kN.m²
Comprimento = 3,0 m
1
1
Resposta
Passo 1: Numeração dos graus de liberdade da estrutura:
3
5
6
9
8
4
2
Esta numeração indica a posição de cada
deslocamento ou esforço na matriz de rigidez
que será elaborada a seguir.
7
2
Podemos afirmar que a estrutura tem 9 graus de
liberdade e, portanto, terá uma matriz de rigidez
de dimensão 9 x 9.
1
2
3
1
1
Passo 2: Incidência das barras
Barra Nó de Início Nó de Fim
1
1
2
2
2
3
Passo 3: Cálculo de [ k ] para cada barra, no sistema local:
Barra 1: Barra Bi-engastada
3
2
6
1
As referências estão indicadas ao lado. A partir
destas referências, tem-se a matriz de rigidez
indicada:
5
4
Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
 EA
 l

 0


 0
k =
EA
 −
l

 0


 0

[]
0
0
12 EI
l3
6 EI
l2
6 EI
l2
4 EI
l
0
0
−
12 EI
l3
6 EI
l2
6 EI
l2
2 EI
l
−
−
EA
l
0
0
EA
l
0
0
2
0
0
12 EI
l3
6 EI
− 2
l
6 EI
l2
2 EI
l
0
0
−
12 EI
l3
6 EI
− 2
l
6 EI
l2
4 EI
l
−















Substituindo-se os valores indicados, tem-se a seguinte matriz de rigidez para a barra 1:
[ k ]1=
75000,00
0,00
0,00
-75000,00
0,00
0,00
0,00
6075,00
12150,00
0,00
-6075,00
12150,00
0,00
12150,00
32400,00
0,00
-12150,00
16200,00
-75000,00
0,00
0,00
75000,00
0,00
0,00
0,00
-6075,00
-12150,00
0,00
6075,00
-12150,00
0,00
12150,00
16200,00
0,00
-12150,00
32400,00
Barra 2 Barra Bi-engastada
3
2
6
Substituindo-se os valores indicados, tem-se a
seguinte matriz de rigidez para a barra 2
5
1
4
100000,00
0,00
0,00
[ k ]2=
-100000,00
0,00
0,00
0,00
14400,00
21600,00
0,00
-14400,00
21600,00
0,00
21600,00
32400,00
0,00
-21600,00
21600,00
-100000,00
0,00
0,00
100000,00
0,00
0,00
0,00
-14400,00
-21600,00
0,00
14400,00
-21600,00
0,00
21600,00
21600,00
0,00
-21600,00
43200,00
Passo 4: Transformando coordenadas locais em coordenadas globais:
Para esta transformação, usa-se a matriz [T] e sua transposta [T]t. A matriz [T] é:
 cosα
− senα

 0
[T] = 
 0
 0

 0
senα
cosα
0
0
0
0
0
0
1
0
0
0
0
0
0
cosα
− senα
0
0
0
0
senα
cosα
0
0
0
0
0
0
1
[]
A transformação ocorre pela multiplicação de matrizes: [k ] = [T ] k [T ]
t









Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
3
Barra 1:
Dado que o ângulo α=90°, tem-se a seguinte matriz [T]:
[T] =
0,00
-1,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
-1,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
-1,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
A matriz transposta [T]t é apresentada a seguir:
[T]t =
0,00
1,00
0,00
0,00
0,00
0,00
-1,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
[]
Assim, pode-se fazer o produto [k ] = [T ] k [T ] . Primeiro começa-se pelo produto
t
[T ] [k ]:
t
0,00
75000,00
[T ]t k = 0,00
0,00
-75000,00
0,00
[]
-6075,00
0,00
12150,00
6075,00
0,00
12150,00
-12150,00
0,00
6075,00 -12150,00
0,00
-75000,00
0,00
0,00
32400,00
0,00
-12150,00 16200,00
12150,00
0,00
-6075,00 12150,00
0,00
75000,00
0,00
0,00
16200,00
0,00
-12150,00 32400,00
Toma-se, então, este resultado e se multiplica por [T]:
6075,00
0,00
-12150,00 -6075,00
0,00
-12150,00
0,00
75000,00
0,00
0,00
-75000,00
0,00
-12150,00
0,00
32400,00
12150,00
0,00
16200,00
[k ] = [T ]t k [T ] = -6075,00 0,00 12150,00 6075,00 0,00 12150,00
0,00
-75000,00
0,00
0,00
75000,00
0,00
-12150,00
0,00
16200,00 12150,00
0,00
32400,00
[]
Essa é a matriz de rigidez da barra 1.
Barra 2:
Dado que o ângulo α=0°, tem-se a seguinte matriz [T]:
[T] =
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
4
A matriz transposta [T]t é apresentada a seguir:
1,00
0,00
0,00
0,00
0,00
0,00
[T]t =
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
1,00
[]
Assim, pode-se fazer o produto [k ] = [T ] k [T ] . Primeiro começa-se pelo produto
t
[T ] [k ]:
t
100000,00
0,00
0,00
[T ]t k = -100000,00
0,00
0,00
0,00
14400,00
21600,00
0,00
-14400,00
21600,00
[]
0,00
-100000,00
0,00
0,00
21600,00
0,00
-14400,00 21600,00
32400,00
0,00
-21600,00 21600,00
0,00
100000,00
0,00
0,00
-21600,00
0,00
14400,00 -21600,00
21600,00
0,00
-21600,00 43200,00
Toma-se, então, este resultado e se multiplica por [T]:
100000,00
0,00
0,00
[k ] = [T ]t [k ][T ] =
-100000,00
0,00
0,00
0,00
14400,00
21600,00
0,00
-14400,00
21600,00
0,00
-100000,00
0,00
0,00
21600,00
0,00
-14400,00 21600,00
32400,00
0,00
-21600,00 21600,00
0,00
100000,00
0,00
0,00
-21600,00
0,00
14400,00 -21600,00
21600,00
0,00
-21600,00 43200,00
Essa é a matriz de rigidez da barra 2.
Passo 5: Montagem da Matriz de Rigidez [K] da estrutura pelo método da colocação:
O Método da Colocação consiste em definir uma matriz com todos os graus de
liberdade (que são 9, neste exemplo) e colocar as matrizes de rigidez de cada barra de
acordo com a incidência das barras (passo 2). No nosso exemplo, tem-se:
nó
1
[K ] =
2
3
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
1
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
2
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
3
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
(
(
(
(
(
(
(
(
(
)
)
)
)
)
)
)
)
)
Barra 1
Barra 2
Soma das
barras
Assim, podemos criar a matriz de rigidez de cada barra, na posição colocada e somá-las
para obter a matriz de rigidez.
Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
5
Para a barra 1:
6075,00
0,00
0,00
75000,00
-12150,00
0,00
-6075,00
0,00
[K]1=
0,00
-75000,00
-12150,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
-12150,00
0,00
32400,00
12150,00
0,00
16200,00
0,00
0,00
0,00
-6075,00
0,00
-12150,00 0,00 0,00 0,00
0,00
-75000,00
0,00
0,00 0,00 0,00
12150,00
0,00
16200,00 0,00 0,00 0,00
6075,00
0,00
12150,00 0,00 0,00 0,00
0,00
75000,00
0,00
0,00 0,00 0,00
12150,00
0,00
32400,00 0,00 0,00 0,00
0,00
0,00
0,00
0,00 0,00 0,00
0,00
0,00
0,00
0,00 0,00 0,00
0,00
0,00
0,00
0,00 0,00 0,00
Para a barra 2:
0,00
0,00
0,00
0,00
[K]2= 0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00 100000,00
0,00
0,00
-100000,00
0,00
0,00
0,00
0,00
14400,00 21600,00
0,00
-14400,00 21600,00
0,00
0,00
21600,00 32400,00
0,00
-21600,00 21600,00
0,00 -100000,00
0,00
0,00
100000,00
0,00
0,00
0,00
0,00
-14400,00 -21600,00
0,00
14400,00 -21600,00
0,00
0,00
21600,00 21600,00
0,00
-21600,00 43200,00
Somando-se as duas matrizes, obtem-se a matriz de rigidez global:
6075,00
0,00
0,00
75000,00
-12150,00
0,00
-6075,00
0,00
[K]=
0,00
-75000,00
-12150,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
-12150,00 -6075,00
0,00
-12150,00
0,00
0,00
0,00
0,00
0,00
-75000,00
0,00
0,00
0,00
0,00
32400,00 12150,00
0,00
16200,00
0,00
0,00
0,00
12150,00 106075,00
0,00
12150,00 -100000,00
0,00
0,00
0,00
0,00
89400,00 21600,00
0,00
-14400,00 21600,00
16200,00 12150,00 21600,00 64800,00
0,00
-21600,00 21600,00
0,00
-100000,00
0,00
0,00
100000,00
0,00
0,00
0,00
0,00
-14400,00 -21600,00
0,00
14400,00 -21600,00
0,00
0,00
21600,00 21600,00
0,00
-21600,00 43200,00
A partir desta matriz, pode-se montar o sistema geral conforme está mostrado na página
seguinte.
A matriz [P] é a matriz dos esforços, [K] é a matriz de rigidez e [p] é a matriz dos
deslocamentos.
Lembrar que [P] = [K] [p].
Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
6
A matriz, então fica:
R1
6075,00
0,00
R2
0,00
75000,00
0,00
R3
-12150,00
0,00
32400,00
0,00
-6075,00
0,00
0,00
-75000,00
0,00
0,00
89400,00 21600,00
0,00
-14400,00 21600,00 x D2
0,00
-12150,00
0,00
16200,00
12150,00
21600,00 64800,00
0,00
-21600,00 21600,00
R7
0,00
0,00
0,00
-100000,00
R8
0,00
0,00
0,00
0,00
-14400,00 -21600,00
0,00
14400,00 -21600,00
0
R9
0,00
0,00
0,00
0,00
21600,00 21600,00
0,00
-21600,00 43200,00
0
-50,00 =
-12150,00 -6075,00
0,00
-12150,00
0,00
0,00
0,00
0
0,00
-75000,00
0,00
0,00
0,00
0,00
0
12150,00
0,00
16200,00
0,00
0,00
0,00
0
12150,00 106075,00
0,00
12150,00 -100000,00
0,00
0,00
D1
0,00
0,00
100000,00
0,00
D3
0,00
0
Note que R1 é a força de reação horizontal no nó 1, R2 é a força de reação vertical no nó 1 e R3 é o momento de reação no nó 1; R7 a força de
reação horizontal no nó 3, R8 é a força de reação vertical no nó 3 e R3 é o momento de reação no nó 3. D1 é o deslocamento horizontal no nó 2,
D2 é o deslocamento vertical no nó 2 e D3 é o deslocamento rotacional no nó 2.
Esta matriz representa um sistema de 9 equações com 9 incógnitas e, portanto, pode ser resolvido. Vamos separar a resolução deste sistema
calculando primeiro os deslocamentos e depois calculando as reações de apoio.
Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
7
Passo 6: Determinação dos deslocamentos dos nós livres
Na matriz abaixo, estão indicadas as linhas onde podem ocorrer deslocamentos.
R1
6075,00
0,00
-12150,00
-6075,00
0,00
-12150,00
0,00
0,00
0,00
R2
0,00
75000,00
0,00
0,00
-75000,00
0,00
0,00
0,00
0,00
0
0
R3
-12150,00
0,00
32400,00
12150,00
0,00
16200,00
0,00
0,00
0,00
0
0,00
-6075,00
0,00
12150,00
106075,00
0,00
12150,00
-100000,00
0,00
0,00
0,00
-75000,00
0,00
0,00
89400,00
21600,00
0,00
-14400,00
21600,00
D1
x D2
0,00
-12150,00
0,00
16200,00
12150,00
21600,00
64800,00
0,00
-21600,00
21600,00
D3
R7
0,00
0,00
0,00
-100000,00
0,00
0,00
100000,00
0,00
0,00
0
R8
0,00
0,00
0,00
0,00
-14400,00 -21600,00
0,00
14400,00
-21600,00
0
R9
0,00
0,00
0,00
0,00
21600,00
0,00
-21600,00
43200,00
0
-50,00 =
21600,00
Note que estas linhas formam um sistema de três equações com três incógnitas.
Isolando estas equações, tem-se o sistema abaixo:
0,00
106075,00
0,00
12150,00
-50,00 =
0,00
89400,00 21600,00 x
0,00
12150,00 21600,00 64800,00
D1
D2
D3
Resolvendo pela inversa da matriz1, tem-se:
D1
9,653E-06 4,756E-07 -1,968E-06
-50,00
D2 = 4,756E-07 1,219E-05 -4,152E-06 x 0,00
D3
-1,968E-06 -4,152E-06 1,719E-05
0,00
Fazendo-se a multiplicação das matrizes, chega-se que:
D1 = -0,00002378 m; D2 = -0,00060944m; D3 = 0,00020761 rad
Passo 7: Determinação das reações de apoio
Para determinar as reações de apoio, devemos substituir D1, D2 e D3 determinados no
passo 6 na matriz definida no passo 5. Essa matriz está colocada na próxima página.
1
Com o MS Excel, pode-se inverter facilmente uma matriz com a função
ÍNDICE(MATRIZ.INVERSO(matriz);linha;coluna). Verificar na ajuda do programa para detalhes de sua
utilização.
Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
8
R1
6075,00
0,00
-12150,00
-6075,00
0,00
-12150,00
0,00
0,00
0,00
0,00
R2
0,00
75000,00
0,00
0,00
-75000,00
0,00
0,00
0,00
0,00
0,00
R3
-12150,00
0,00
32400,00
12150,00
0,00
16200,00
0,00
0,00
0,00
0,00
0,00
-6075,00
0,00
12150,00 106075,00
0,00
12150,00 -100000,00
0,00
0,00
-0,00002378
0,00
-75000,00
0,00
0,00
89400,00 21600,00
0,00
-14400,00 21600,00 x -0,00060944
0,00
-12150,00
0,00
16200,00
12150,00
21600,00 64800,00
0,00
-21600,00 21600,00
R7
0,00
0,00
0,00
-100000,00
R8
0,00
0,00
0,00
0,00
-14400,00 -21600,00
0,00
14400,00 -21600,00
0,00
R9
0,00
0,00
0,00
0,00
21600,00 21600,00
0,00
-21600,00 43200,00
0,00
-50,00 =
0,00
0,00
100000,00
0,00
Procedendo-se à multiplicação das matrizes, chega-se ao resultado:
R1
=
-2,378
kN
R2
=
45,708 kN
R3
=
3,074
kN.m
-50,00
=
0,000
kN
0,00
=
0,00
=
0,000
kN.m
R7
=
2,378
kN
R8
=
4,292
kN
R9
=
-8,680
kN.m
-50,000 kN
0,00
0,00020761
0,00
Exercício Exemplo de Análise Matricial de Estrutura
Prof. Luís Henrique Piovezan - UNIBAN
9
A representação física deste resultado em um diagrama de corpo livre é dada pelo
diagrama:
50 kN
4,292 kN
2,378 kN
8,680 kN.m
2,378 kN
3,074 kN.m
45,708 kN
A partir do diagrama de corpo livre, pode-se desenhar os esforços solicitantes na
estrutura.