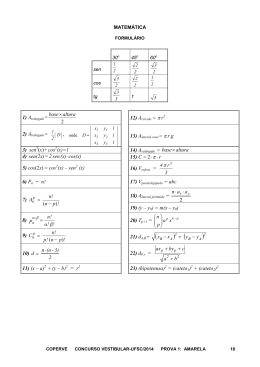
MATEMÁTICA
FORMULÁRIO
30o
45o
60o
sen
1
2
2
2
cos
3
2
2
3
2
1
2
tg
3
3
1
3
2
1
, sen x ≠ 0
sen x
1
sec x =
, cos x ≠ 0
cos x
sen x
tg x =
, cos x ≠ 0
cos x
cos x
, sen x ≠ 0
cotg x =
sen x
cosec x =
sen2 x + cos2 x = 1
10) A∆ =
b⋅h
2
ou
1) an = a1 + (n – 1) . r
onde
 a + an 
2) Sn =  1
. n

2
x1
y1
1
x2
y2
1
x3
y3
1
2
11) Acírculo = πr , Ccírculo = 2πr

2
D=
A∆ = 1 D
2
2
12) (x – a) + (y – b) = r
n –1
2
3) an = a1 . q
n
13) Se P(x) = anx + an – 1x
4) S =
n-1
+ ... + a1x + a0 e
x1 , x2 , ... , xn são raízes de P(x), então
(- 1)n a0
x1 . x2 . ... . xn =
an
a1
1- q
A .h
5)
Anp
14) Vcone =
n!
=
(n − p)!
b
3
A .h
6) Pn = n!
15) Vpirâmide =
n!
p
7) Cn =
p! (n − p)!
16) Vesfera
8) dA,B=
9) dP,r =
b
3
4 π r3
=
3
2
( xB − x A )2 + ( yB − y A )2
17) Vcilindro = πr h
ax0 + by0 + c
18) Soma dos ângulos internos de um polígono regu-
2
a +b
COPERVE/UFSC
2
lar de n lados = (n–2).180o
CONCURSO VESTIBULAR-UFSC/2006
2a PROVA: AMARELA
Questão 01
Questão 02
Assinale a(s) proposição(ões) CORRETA(S).
Seja f uma função polinomial do primeiro grau,
decrescente, tal que f(3) = 2 e f(f(1)) = 1.
Determine a abscissa do ponto onde o gráfico de
f corta o eixo x.
01. Se K = (kij) é uma matriz quadrada de ordem
2i + j
para i < j e
2 dada por kij = 2
2
kij = i + 1 para i ≥ j, então K é uma matriz
inversível.
02. Se A e B são matrizes tais que A.B é a matriz
nula, então A é a matriz nula ou B é a matriz
nula.
Assinale o resultado encontrado no cartãoresposta.
Comentário:
04. Sejam as matrizes M e P, respectivamente,
de ordens 5 x 7 e 7 x 5. Se R = M.P, então
2
a matriz R tem 625 elementos.
08. Chamamos “traço de L” e anotamos tr(L) a
soma dos elementos da diagonal principal de
t
uma matriz quadrada L; então tr(L) = tr(L ).
Comentário:
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
2
Questão 03
Assinale a(s) proposição(ões) CORRETA(S).
01. Se f(x) = 3x + a e a função inversa de f é
g(x) =
x
+1, então a = –3.
3
02. Se (an) e (bn) são duas progressões
aritméticas, então (an + bn) é uma progressão aritmética.
04. A equação
solução real.
08.
16.
4 3 + x − 4 x −3
4 x + 4 x −3
x2 + 1 = x − 1
não tem
= 64 para todo x real.
n2 − 1
= n − 1 para todo número inteiro n.
n+1
Comentário:
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
3
Questão 04
2
A base quadrada de uma pirâmide tem 144 m de
área. A 4 m do vértice traça-se um plano paralelo
2
à base e a secção assim feita tem 64 m de área.
Qual a altura da pirâmide?
Assinale o resultado encontrado no cartãoresposta.
Comentário:
04.
• L2 = 144 ⇒ L = 12
• l2 = 64 ⇒ l = 8
•
H L
=
h l
H 12
=
4
8
8H = 48 ⇒ H = 06 m
R: 06
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
4
Questão 05
Assinale a(s) proposição(ões) CORRETA(S).
01. Se uma pessoa A pode fazer uma peça em 9
dias de trabalho e outra pessoa B trabalha
com velocidade 50% maior do que A, então B
faz a mesma peça em 6 dias de trabalho.
02. Uma empresa dispunha de 144 brindes para
distribuir igualmente entre sua equipe de
vendedores, mas como no dia da distribuição
faltaram 12 vendedores, a empresa distribuiu
os 144 brindes igualmente entre os
presentes, cabendo a cada vendedor um
brinde a mais. Logo, estavam presentes 36
vendedores no dia da distribuição.
04. Se reduzindo o preço x em 20% se obtém y,
então y deve sofrer um acréscimo de 20%
para se obter novamente x.
08. A soma de dois números naturais é 29. Então
o valor mínimo da soma de seus quadrados é
533.
Comentário:
COPERVE/UFSC
01) VERDADEIRA
t
tB = A
1,5
9
tB =
3
2
tB = 6
02) VERDADEIRA
nº vendedores
144
144
+1
=
n – 12
n
n – 12 = 36
n = 48
144 144
+1
=
36
48
4=3+1
04) FALSA
•P
• Reduzindo 20% : 0,80 . P
• Aumentando 20% : 0,80 . P + 0,20 . 0,80 P = 0,96 P
08) FALSA
x + y = 29
y = 29 – x
S = x2 + y2
S = x2 + (29 – x)2
S = x2 + 841 – 58x + x2
S = 2x2 – 58x + 841
Cálculo do xy:
b
xv = –
2a
−58
x=–
2.2
29
x=
(não é natural)
2
R: 03 (01, 02)
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
5
Questão 06
Dois líquidos diferentes encontram-se em recipientes idênticos e têm taxas de evaporação
constantes. O líquido I encontra-se inicialmente
em um nível de 100 mm e evapora-se completamente no quadragésimo dia. O líquido II,
inicialmente com nível de 80 mm, evapora-se
completamente no quadragésimo oitavo dia.
Determinar, antes da evaporação completa de
ambos, ao final de qual dia os líquidos terão o
mesmo nível (em mm) nesses mesmos recipientes.
Assinale o resultado encontrado no cartãoresposta.
06.
 x 1: nº do dia
Líquido I: 
 y 1: nível do líquido I.
y1 = a.x1 + b
Se x1 = 0 → y1 = 100 → 100 = a.0 + b → b =100
Se x1 = 40 → y1 = 0 → 0 = a.40 + b
100
→ 0 = 40a + 100 → a = –
40
→ a=–5
2
Logo y1 = –
5
. x1 + 100
2
 x 2 : nº do dia
Líquido II: 
 y 2 : nível do líquido II.
Comentário:
y2 = m.x2 + n
Se x2 = 0 → y2 = 80 → 80 = m.0 + n → n = 80
Se x2 = 48 → y2 = 0 → 0 = m.48 + n → 0 = 48m + 80
80
→m=–
→ m=–5
48
3
5
y2 = – x + 80
3
Para obter o dia em que os líquidos terão o
mesmo nível, devemos resolver o sistema formado pelas equações:
5

 y = – 2 x + 100

 y = – 5 x + 80

3
5
5
– x + 100 = – x + 80
2
3
5
5
x – x = 80 – 100
2
3
5x
= – 20
–
6
x
=4
6
x = 24
Logo, no 24º dia.
R: 24
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
6
Questão 07
01. Se o conjunto A tem 5 elementos e o conjunto B tem 4 elementos, então o número de
funções injetoras de A em B é 120.
1
02. Se 16 = 9 e log32 = y, então xy = .
2
x
04. Se aumentarmos em 4 cm o comprimento de
uma circunferência, seu raio aumentará
4
cm.
2π
08. Um grupo formado por 4 rapazes e uma
senhorita vai visitar uma exposição de arte.
Um dos rapazes é um perfeito cavalheiro e,
portanto, não passa pela porta da sala de
exposições sem que a senhorita já o tenha
feito. Considerando que a entrada é de uma
pessoa por vez, então haverá 72 diferentes
possibilidades para a ordem de entrada do
grupo.
22
16. 125 é divisor de 15 .
Comentário:
01) FALSA
n (A) = 5
n (B) = 4
Como n(A) > n(B), a função f: A → B não pode ser
injetora.
02) VERDADEIRA
• 16x = 9
log316x = log39
x . log3 24 = log332
4x . log32 = 2log33
1
x=
2 . log 3 2
•x.y=
x.y=
1
. log32
2 . log 3 2
1
2
04) VERDADEIRA
• C1 = 2πR1
• 2πR1 + 4 = 2πr2
4
= R2
R1 +
2π
2
R1 + = R2
π
08) FALSA
RPC, R1, R2, R3, S
→ S, __, __, __, __ P4
→ R, S, __, __, __ 3 . P3
→ R, R, S, __, __ 3 . 2 . P2
→ R, R, R, S, __ P3
n = 4! + 3.3! + 6.2!+3!
n = 24 + 18 + 12 + 6
n = 60
16) VERDADEIRA
1522 = (3.5)22 = 322.522 = 322 . 519 . 53 = 322 . 519 . 125
R: 22 (02, 04, 16)
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
7
Questão 08
Determine o número de pontos de intersecção
2
2
dos gráficos das equações x + y = 9 e
2
x – 3 = 0 no plano cartesiano.
Assinale o resultado encontrado no cartãoresposta.
Comentário:
 2
 x = 3
(II)
Substituindo (II) em (I):
3 + y2 = 9
y = 6
y2 = 6 → 
 y = – 6
Os pontos de intersecção são ( 3; 6), ( 3; – 6),
(– 3; 6) e (– 3; – 6)
Portanto, são 4 pontos.
R: 04
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
8
Questão 09
Assinale a(s) proposição(ões) CORRETA(S).
01) VERDADEIRA
01. Um poste na posição vertical, colocado num
plano horizontal, encontra-se a 3 m de uma
parede plana e vertical. Neste instante, o sol
projeta a sombra do poste na parede e esta
sombra tem 17 m de altura. Se a altura do
poste é de 20 m, então a inclinação dos raios
solares, em relação ao plano horizontal, é de
45o.
02. Se sen(a) =
1
, então
3
2
sen (25π + a) – sen (88π – a) = .
3
04. Os gráficos das funções f(x) = sen(4x) e
2x π
+ têm exatamente 3 pontos em
g(x) = −
3 4
comum, para x no intervalo (0, à/2).
tgα =
3
=1
3
Logo, α = 45o
02) Falsa
sen (25π + α) = sen (π + α) = – sen α
sen (88π – α) = sen (2π – α) = – sen α
Logo
sen (25π + α) – sen (88π – α) = – sen α –(– sen α) = 0
04) VERDADEIRA
08. Para ser verdadeira a desigualdade
tg(x).sec(x) < 0, x deve estar localizado no
segundo ou no quarto quadrante.
Comentário:
g(0) =
π
4
 3π 
g  = 0
 8
08) FALSA
R: 05 (01, 04)
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
9
Questão 10
Considere um hexágono eqüiângulo (ângulos
internos iguais) no qual quatro lados consecutivos medem 20 cm, 13 cm, 15 cm e 23 cm,
conforme figura abaixo. Calcule o perímetro do
hexágono.
20
E
Prolongando-se os lados do hexágono, obtemos a
estrela:
D
13
C
F
15
A
23
B
Assinale o resultado encontrado no cartãoresposta.
Os triângulos AEC, DBF são equiláteros
AE = FD = AC
e
x + 20 + 13 = 20 +13 +15 = x + y + 23
x + 33 = 48 = x + y + 23
(1)
Comentário:
COPERVE/UFSC
(2)
(1) x + 33 = 48
x = 15
(2) 48 = x + y + 23
48 = 15 + y + 23
y = 10
Perímetro = 20 + 13 + 15 + 23 + 10 + 15 = 96
R: 96
CONCURSO VESTIBULAR-UFSC/2006
1a PROVA: AMARELA
10