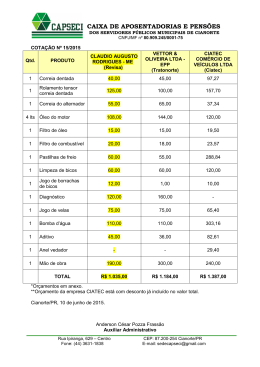
CORRESPONDÊNCIA ENTRE PONTOS
NO SEGUIMENTO DE MOVIMENTO EM IMAGENS
Raquel Ramos Pinho1,3, João Manuel R. S. Tavares1,3, Miguel V. Correia2,3
1
Instituto de Engenharia Mecânica e Gestão Industrial, Lab. Óptica e Mecânica Experimental
2
Instituto de Engenharia Biomédica, Lab. Sinal e Imagem
3
Universidade do Porto, Faculdade de Engenharia
Resumo
Para realizar o seguimento de movimento ao longo de sequências de imagens podem ser
utilizadas inúmeras técnicas. Neste trabalho, recorremos ao uso de modelos estocásticos sob
uma perspectiva bayesiana que, independentemente da complexidade do movimento, visam
superar as dificuldades de estimação, medição e controlo. Assim, o seguimento entre imagens
consecutivas pode subdividir-se na fase de previsão do modelo na imagem seguinte, e na fase
de correcção a partir de dados medidos nessa imagem. Com este trabalho, pretende-se
estabelecer a correspondência entre pontos de cada uma das fases anteriormente
enumeradas, usando o filtro de Kalman e considerando um critério global de determinação
de correspondências.
podem ser definidas de diversas formas (ver
por exemplo (Tavares, 1995)); no entanto, a
generalidade dos métodos recorre à
posição, podendo também ser incluídas a
velocidade e a aceleração (Correia, 1995;
Tavares, 1995).
Segundo uma perspectiva bayesiana, a
transição de estados do sistema, a que
corresponderá o seguimento do movimento,
é realizada através da consideração de duas
fases entre cada par de imagens
consecutivas: uma, de previsão do estado
do sistema na imagem seguinte; e outra, de
correcção da estimativa feita anteriormente,
mediante a consideração de dados
recolhidos a posteriori.
Em cada fase de correcção, podem ser
incluídas medições; contudo, para o fazer é
necessário estabelecer as correspondências
entre os pontos a serem seguidos. Neste
trabalho, considera-se o filtro de Kalman no
seguimento de pontos e, para além dos
critérios locais usualmente utilizados nos
referidos emparelhamentos, também se
considera uma análise global dos mesmos,
de forma a optimizar o resultado integral
obtido.
Esta abordagem poderá ser estendida a
diferentes aplicações. Por exemplo, na
INTRODUÇÃO
A análise de movimento tem sido uma área
em vasta expansão ao longo dos últimos
anos no domínio Visão Computacional. A
motivar estes trabalhos, encontra-se a
crescente necessidade de automatizar
computacionalmente processos de análise
de movimento. A análise de movimento
poderá consistir nas etapas de detecção, de
seguimento e de reconhecimento ao longo
de sequências de imagens (Pinho, 2004).
Para seguir movimento de forma
automática, deve-se atender a algumas
dificuldades:
não
existem
modelos
computacionais perfeitos e, mesmo quando
estes são adequados a certas aplicações, são
baseados em aproximações da realidade;
existem perturbações que não podem ser
controladas
nem
modeladas
deterministicamente; os dados adquiridos
não são perfeitos. Desta forma, e dado que
as
abordagens
determinísticas
não
ultrapassam as dificuldades mencionadas,
os modelos estocásticos têm sido cada vez
mais utilizados (Maybeck, 1979).
Neste trabalho, para se proceder ao
seguimento do movimento, considera-se o
sistema como sendo constituído por pontos.
Relativamente às variáveis de estado, estas
1
informações extra a partir de novos dados,
(Maybeck, 1979).
análise de impacto, para testes de controlo
de qualidade; ou na análise da marcha, no
auxílio de diagnóstico clínico.
FILTRO DE KALMAN
O filtro de Kalman assume que a função
densidade de probabilidade em cada
instante de tempo segue uma distribuição
normal. Este filtro permite a estimativa do
estado de um sistema de forma a minimizar
o quadrado da média do erro (Welch,
1995).
A fase de predição é gerada por intermédio
da equação Chapman-Kolmogorov e,
considerando que se utiliza um processo de
Markov de primeira ordem, obtém-se:
SEGUIMENTO BAYESIANO
Sob uma perspectiva bayesiana discreta, o
seguimento consiste no cálculo recursivo de
grau de certeza associado a cada estado em
determinado
instante,
tendo
em
consideração os dados obtidos até esse
momento. Para tal, é assumido que as
técnicas de modelação produziram um
sistema descritivo, sob a forma de uma
equação diferencial estocástica para
descrever a propagação de estados (modelo
do sistema), e que são disponibilizadas
medições discretas corrompidas por ruído
(modelo de medições). Assim, tem-se por
objectivo combinar as medições obtidas no
sistema actual com a informação
providenciada pelo modelo do sistema, e a
descrição estatística das incertezas no
sentido de obter estimativas óptimas
(Maybeck, 1979; Correia, 1995; Tavares,
1995).
Em geral, a optimização da estimativa
obtida depende do critério utilizado. Neste
caso, como se utiliza uma abordagem
bayesiana,
procuram-se
meios
de
propagação da função densidade de
probabilidade condicional, restringida pelo
processo de medição.
Os filtros deste tipo são compostos por duas
fases: uma de predição e outra de correcção.
A predição utiliza o sistema do modelo para
prever a função de densidade de
probabilidade do estado no instante
seguinte. Dado que o estado é, de um modo
geral, sujeito a algumas perturbações
(usualmente modeladas como ruído
aleatório), a predição considera a
translação, a deformação e difusão da
função densidade de probabilidade. Por
outro lado, a fase de correcção utiliza a
medição mais actual de forma a modificar a
função densidade de probabilidade prevista.
Tal é conseguido pela utilização do teorema
de Bayes, que consiste no mecanismo de
actualização da informação acerca do
estado objectivo quando são fornecidas
xt− = Φxt+−1 ,
(1)
onde xt+−1 corresponde ao vector de
variáveis de estado do sistema no instante
t − 1 posterior à fase de medição, e xt−
corresponde à estimativa para o instante t
antes da medição na imagem do instante
associado, sendo sua transição dada por Φ .
A estimativa para a incerteza associada à
previsão do vector xt− é dada por:
Pt − = ΦPt +−1ΦT + Q ,
(2)
onde P é a matriz de covariância (mais uma
vez os índices + e − são relativos à
incorporação ou não das medições nesta
iteração do filtro).
A fase seguinte do filtro de Kalman,
corresponde à correcção das estimativas
realizada através da eventual incorporação
de novas medições ut :
K t = Pt − H T ⎡⎣ HPt − H T + Rt ⎤⎦
−1
,
(3)
xt+ = xt− + K t ⎡⎣ut − Hxt− ⎤⎦ ,
(4)
Pt + = [ I − K t H ] Pt − ,
(5)
onde K é o ganho do filtro, H é a matriz
que transforma o sistema de coordenadas
do vector de características estimadas no
vector de características medido, e Rt é a
matriz de variância medida (Correia, 1995;
Tavares, 1995; Arulampalam, 2002).
2
CONCLUSÕES E PERSPECTIVAS DE
TRABALHO FUTURO
Neste trabalho é proposto um modo de
contornar algumas dificuldades inerentes ao
processo
de
determinação
de
correspondências
entre
pontos
em
sequências de imagem. Tais dificuldades,
eventualmente resultantes de mecanismos
de deformação, de rotação ou de oclusão
implícitos ao movimento em causa, são
superadas através da consideração de um
algoritmo de optimização global no
estabelecimento dos emparelhamentos.
Os resultados experimentais obtidos, e que
serão apresentados, demonstram que a
metodologia proposta é adequada.
No futuro, será interessante aplicar a
mesma abordagem nos processos de
seguimento que consideram outros filtros,
por exemplo filtros de partículas.
ESTABELECIMENTO DE
CORRESPONDÊNCIAS
Para fazer a introdução de novas medições
na fase de correcção do filtro de Kalman é
necessário seleccionar, entre as eventuais
entidades candidatas ao emparelhamento,
aquela que apresenta características que
melhor se aproximam às estimadas.
Pela construção do filtro de Kalman, para a
posição ( x, y ) das entidades, a área de
pesquisa sobre o plano de imagem para o
estabelecimento de correspondências é uma
elipse, cujos eixos são determinados pelos
vectores próprios da matriz reduzida de
covariância, os raios são dados pelos
valores próprios associados, e o centro
corresponde à posição prevista pelo filtro
para a entidade (Correia, 1995; Tavares,
1995). Caso exista convergência, estas
áreas de pesquisa vão diminuindo ao longo
do tempo, dado que são obtidas estimativas
cada vez mais adequadas, e desta forma o
custo
computacional
associado
à
correspondência entre pontos é cada vez
menor (Correia, 1995; Tavares, 1995).
Contudo, esta abordagem poderá apresentar
algumas dificuldades: a não existência de
nenhuma entidade adequada no interior da
área de pesquisa; ou pelo contrário, a
existência de múltiplas entidades. E, mesmo
quando o emparelhamento é conseguido no
interior
da
respectiva
área
de
emparelhamento, não há garantia de que se
tenha obtido para o sistema como um todo
o melhor conjunto de correspondências.
Assim, neste trabalho pretende-se superar
tais dificuldades, com especial ênfase na
determinação dos emparelhamentos de
forma global. Para tal, através da aplicação
de um método de optimização global, tentase assegurar a obtenção do melhor conjunto
de correspondências para todas as entidades
envolvidas. Neste processo, é necessário
pesar a possibilidade de duas quaisquer
entidades serem emparelhadas entre si. Tal
peso, ou seja o custo do emparelhamento,
será obtido pela consideração da distância
normalizada de Mahalanobis (Tavares,
1995).
BIBLIOGRAFIA
M. Arulampalam, S. Maskell, N. Gordon, T.
Clapp, A Tutorial on Particle Filters for
Online Nonlinear/Non-Gaussian Bayesian
Tracking, IEEE Transactions on Signal
Processing 50 (2002) 174/188.
M. Correia, Análise de Movimento em
Sequências de Imagens, Dissertação de
Mestrado, Faculdade de Engenharia,
Universidade do Porto, 1995.
P. Maybeck, Stochastic Models, Estimation,
and Control, Vol. 1 (1979).
R. Pinho, J. Tavares, M. Correia, Introdução à
Análise de Movimento por Visão
Computacional, Relatório Interno,
Faculdade de Engenharia, Universidade do
Porto, 2004.
J. Tavares, Obtenção de Estrutura
Tridimensional a partir de Movimento de
Câmara, Dissertação de Mestrado,
Faculdade de Engenharia, Universidade do
Porto, 1995.
G. Welch, G. Bishop, An Introduction to
Kalman Filter, Technical Report,
University of North Carolina at Chapel
Hill, 1995.
3