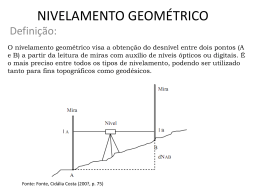
Topografia I
Profa. Andréa Ritter Jelinek
45
Capítulo III
ALTIMETRIA
1. Introdução
A altimetria ou nivelamento tem por finalidade determinar a distância vertical ou
diferença de nível entre diversos pontos. A diferença de altura entre dois pontos é a diferença
de nível entre estes pontos.
A determinação das diferenças de nível entre dois pontos é possível com os seguintes
métodos:
(a) nivelamento geométrico; e
(b) nivelamento trigonométrico.
Influência da Curvatura da Terra e da Refração Atmosférica
Na fig. 3.1, querendo-se determinar a diferença de nível entre os pontos A e B, colocase em B uma mira em posição vertical e em A um instrumento devidamente nivelado, dando a
horizontal AH, correspondente a superfície de nível aparente, que irá interceptar a mira em um
ponto C, e não em B, pois o arco AB não pode ser determinado pelos aparelhos de topografia.
É evidente que a substituição do nível verdadeiro pelo nível aparente provoca um erro
na determinação da altura de um ponto do terreno, o qual é denominado erro devido à
curvatura da terra.
O erro cometido, ao se admitir que os pontos A e C estão em nível (nível aparente), é o
erro EC = BC, denominado erro devido à curvatura da terra.
Este erro pode ser calculado, desde que seja medida a extensão do alinhamento AC =
D, uma vez que o raio da terra é conhecido.
Assim:
D2 = (OB + BC)2 - OA2
ou:
D2 = (R + EC)2 - R2
desenvolvendo:
D2 = EC (EC + 2.R)
e:
EC = D2 / (EC + 2.R)
Topografia I
Profa. Andréa Ritter Jelinek
46
Como o erro é uma quantidade muito pequena em relação ao raio da Terra, pode-se,
sem cometer erro sensível, desprezar EC no denominador, e a fórmula para o cálculo do erro
devido à curvatura da terra é:
EC = D2 / 2.R
Figura 3.1
Na prática das operações altimétricas, o erro devido à curvatura da Terra, apresenta-se
diminuído, em razão do efeito da refração atmosférica sobre o raio visual.
Quando se faz uma visada de um ponto para outro, o raio visual ao atravessar as
camadas atmosféricas de densidades diferentes se refrata, seguindo uma trajetória curva,
situada sobre o plano vertical visual, cuja concavidade é dirigida sobre a superfície do solo.
Como conseqüência, o ponto C, quando visado de A é visto em C’, originando o erro de
refração: ER = CC’. A superfície AC’ é dita superfície de nível ótico.
Este erro é dependente da temperatura e do estado higrométrico do ar, além de outras
circunstâncias locais. Em condições normais, a equação do erro de refração é a seguinte:
ER = 0,1306.EC
sendo que 0,1306 representa o raio de curvatura de refração médio diário.
A correção a ser feita na determinação da altura do ponto B, visto de A, será:
C = EC - ER
C = D2 / 2R - 0,1306.D2 / 2R = D2 / 2.R.(1 - 0,1306)
C = 0,43.D2 / R
C = 0,068.DH2(Km)
ou
C = 6,8.10-8.DH2 (m)
Topografia I
Profa. Andréa Ritter Jelinek
47
Conhecendo-se o valor de R (aproximadamente 6.370 Km), pode-se determinar o erro
devido à curvatura da terra e à refração atmosférica, para qualquer visada efetuada, por
exemplo: para uma visada de 100 m, o erro será igual a 0,0007 m; para uma visada de 120 m,
o erro será igual a 0,0010 m; já para uma visada de 1000 m, o erro será igual a 0,068 m.
Assim, para distâncias menores que 120 m o erro devido à curvatura da terra e à refração
atmosférica pode ser desprezado, por ser inferior ao milímetro.
2. Nivelamento Geométrico
O nivelamento geométrico é baseado na diferença de leituras em miras verticais
graduadas. A precisão obtida é bastante grande, da ordem de milímetros nos trabalhos
especiais de 1ª ordem, até apenas alguns centímetros nos topográficos comuns.
De modo geral, os instrumentos empregados nos trabalhos de nivelamento geométrico
são denominados níveis. Utilizam-se, também, nas operações de nivelamento, associadas aos
níveis, as miras.
O objetivo dos níveis é fornecer um plano horizontal, para as operações topográficas.
O fio central do retículo da luneta define um plano horizontal de referência.
Os níveis podem ser óticos, digitais e laser.
O nível ótico constitui o equipamento clássico de nivelamento. Consiste basicamente
em uma luneta montada sobre um tripé, com possibilidade de ser nivelada com precisão,
através de parafusos calantes e bolhas.
A precisão destes equipamentos depende do sistema de nivelamento, da sensibilidade
das bolhas e da precisão das miras.
Alguns níveis óticos possuem um compensador ou nivelador automático, que permite o
posicionamento horizontal automatizado em frações de segundo, desde que o nivelamento
“grosseiro” esteja dentro da margem de tolerância.
O princípio de funcionamento de um nível eletrônico é o processamento unidimensional
de imagens, a partir de uma mira codificada em código de barras. A leitura da mira codificada é
feita através de uma rede de sensores óticos, a qual reconhece a codificação da mira através
de um processo de correlação de imagens entre a imagem da mira e uma imagem padrão
gravada na memória do instrumento.
Em termos de precisão, os níveis eletrônicos possuem
precisões que variam de 0,4 mm a 0,9 mm em nivelamento duplo e com miras de invar.
Os níveis a laser consistem em um novo tipo de equipamento, projetado para definir
planos horizontais, verticais ou com certa inclinação. São compostos por duas unidades, a
unidade projetora, que é um aparelho emissor de um feixe de raio laser que passa através de
um prisma rotatório definindo assim um plano horizontal materializado pela radiação; e a
unidade detectora, que pode ser afixada numa baliza e movida para cima e para baixo, com
relação ao plano previamente materializado. O feixe de laser incide verticalmente num prisma
Topografia I
Profa. Andréa Ritter Jelinek
48
pentagonal e após duas reflexões nas faces, emerge na direção horizontal. A horizontalidade
do equipamento é condição crítica para o bom funcionamento e costuma ser conseguida por
um dos três métodos: normalmente com três parafusos calantes de nível tubular; através de
um compensador ótico baseado no efeito da gravidade sobre um pêndulo interno ou um
compensador eletrônico. Tem um alcance de até 450 m, com precisão de 1 mm para distâncias
de até 100 m , e de 3 mm para distâncias maiores.
As miras são réguas de madeira ou metal usadas no nivelamento para determinação
de distâncias verticais, medidas entre a projeção do traço do retículo horizontal da luneta na
mira e o ponto do terreno onde a mira está instalada.
As miras mais utilizadas são as “miras falantes”. Estas, geralmente apresentam o
comprimento de 4 metros, sendo graduadas em centímetros. Os centímetros são pintados
alternadamente em preto e branco, os decímetros numerados em preto e os metros
assinalados por círculos pintados em preto ou vermelho.
As miras normalmente são de encaixe. São constituídas de três peças, encaixadas a
primeira dentro da segunda e esta na terceira. Um dispositivo com mola fixa uma peça na outra
quando a mira está completamente distendida, de maneira que a graduação de uma seja a
continuação de outra.
Existem miras com graduação direta e graduação indireta, para leitura com
instrumentos de luneta de imagem direta ou indireta, respectivamente.
A leitura na mira é constituída por quatro algarismos e um número de três casas
decimais: metro, decímetro, centímetro e milímetro. O ponto indica o número de metros; o
algarismo o número de decímetros; os traços pretos e brancos alternados, o número de
centímetros e o número de milímetros são estimados.
Nivelamento Geométrico Simples
Nivelamento Geométrico Simples é aquele em que de uma única estação do nível é
possível visar a mira colocada sucessivamente em todos os pontos do terreno a nivelar.
Assim, considerando-se a fig. 3.2, desejando-se determinar a diferença de nível entre
os pontos A e B, instala-se o nível, em uma posição qualquer do terreno, preferencialmente
eqüidistante dos pontos a nivelar. Determina-se a leitura da mira em A e B. A diferença de nível
entre A e B será calculada pela diferença entre as leituras processadas nos pontos A e B.
No nivelamento geométrico, o perfil do terreno a ser estudado é piqueteado de 10 em
10 metros ou de 20 em 20 metros, conforme a natureza do trabalho. Em seguida, o nível é
estacionado em um ponto conveniente, sobre a linha a nivelar ou fora dela. Desta única
posição do instrumento são determinadas as leituras na mira colocada, primeiramente num
ponto de cota conhecida e, depois, sucessivamente, nos demais pontos.
A visada na primeira estaca, geralmente de cota conhecida, é por convenção chamada
de “visada de ré”. Todas as visadas a partir da visada de ré são chamadas “visadas de vante”.
Topografia I
Profa. Andréa Ritter Jelinek
49
Desta forma, para cada estação de nivelamento, tem-se uma visada de ré e uma ou mais
visadas de vante.
Para o cálculo das cotas dos pontos nivelados é necessário ainda, realizar a medição
da altura do instrumento, ou seja, a altura do eixo ótico acima do plano de referência. Para
determinar a altura do instrumento, faz-se uma leitura inicial num ponto de cota conhecida.
Para que as leituras do levantamento tenham significado, é necessário que elas sejam
referenciadas a um plano, chamado referência de nível.
Figura 3.2
Quando se usa o nível médio do mar, a referência de nível é igual a zero. Quando a
referência de nível é arbitrária, atribui-se um valor inicial elevado, de modo que no decorrer do
levantamento não ocorram cotas negativas.
Portanto, duas são as regras para nivelar:
(i) a altura do instrumento (Ai) é igual à soma da visada de ré (RÉ) com a cota do ponto
(C) onde a mesma foi feita:
Ai = C + RÉ
(ii) a cota de um ponto (C), em função da altura do instrumento (Ai), é a diferença entre
tal altura e a visada a vante (VANTE) lida no mesmo ponto:
C = Ai - VANTE
Nivelamento Geométrico Composto
Topografia I
Profa. Andréa Ritter Jelinek
50
O nivelamento geométrico composto consiste em uma série de nivelamentos
geométricos simples, devidamente amarrados uns aos outros. Este processo é empregado
quando se trata de nivelamento em terreno de desnível acentuado, em que a determinação da
diferença de nível total exige mais de uma estação do aparelho.
Desejando-se determinar a diferença de nível de A para B e, tratando-se de terreno
acidentado, por melhor que seja posicionado o aparelho no terreno, não se consegue visar
simultaneamente, os pontos considerados, pois a diferença de nível entre os pontos A e B é
superior a altura da mira, conforme mostra a fig. 3.3.
Figura 3.3
Assim, com o nível na estação 1, visa-se a mira colocada no ponto A, que representará
a leitura de ré. Em seguida faz-se a leitura de vante no ponto M; como esta será a última
visada de vante com o nível na estação 1, será chamada de “vante de mudança”. Muda-se
depois o nível para a estação 2, de onde se fará uma visada de ré no ponto M e,
posteriormente uma visada de vante no ponto B.
Desta forma, concluiu-se que para atingir o objetivo foi necessário proceder a dois
nivelamentos geométricos simples, devidamente ligados pela estaca de mudança M, em que
se procedeu a visada de vante de mudança na estação 1, e a visada de ré da estação 2; temse deste modo, o nivelamento geométrico composto.
Para proceder à compensação de erros em um nivelamento, é necessário iniciar e
terminar o levantamento no mesmo ponto. Como, normalmente procede-se ao nivelamento de
perfis, ou poligonais abertas, após o nivelamento de cada um dos pontos piqueteados em um
Topografia I
Profa. Andréa Ritter Jelinek
51
perfil, é realizado outro nivelamento em sentido contrário, denominado de “contra-nivelamento”,
quando são nivelados apenas alguns dos pontos; e “renivelamento”, quando o retorno se dá
nivelando todos os pontos.
2.1. Cálculo do Nivelamento Geométrico
As grandezas medidas em um nivelamento geométrico são registradas em uma
planilha, para depois efetuarem-se os cálculos. O exemplo da fig. 3.4 é o nivelamento e contranivelamento de um perfil, onde a cota do ponto A é conhecida, igual a 50,000 m, e o
espaçamento entre os piquetes é de 20 m.
Planilha:
EST
1
2
3
4
∑
PN
A
B
C
C
D
E
F
G
G
C
C
A
LEITURAS NA MIRA
RÉ
1,820
VI
(m)
VM
Ai
(m)
51,820
3,725
3,749
0,833
CORREÇÃO
COTAS
(m)
50,000
48,095
48,071
(m)
--0,001
0,001
CORRIGIDAS (m)
46,403
46,870
45,218
44,914
0,002
0,002
0,002
0,002
46,401
46,868
45,216
44,912
48,071
0,003
48,068
50,004
0,004
50,000
--48,094
48,070
48,904
2,501
2,034
3,686
3,990
3,458
48,372
0,301
2,867
50,938
0,934
8,978
COTAS
8,974
Topografia I
Profa. Andréa Ritter Jelinek
52
Figura 3.4
Cálculo do Nivelamento:
Ai1 = CA + RÉA = 50,000 + 1,820 ∴ Ai1 = 51,820
CB = Ai1 - VB = 51,820 - 3,725 ∴ CB = 48,095
CC = Ai1 - VC = 51,820 - 3,749 ∴ CC = 48,071
Ai2 = CC + RÉC = 48,071 + 0,833 ∴ Ai2 = 48,904
CD = Ai2 - VD = 48,904 - 2,501 ∴ CD = 46,403
CE = Ai2 - VE = 48,904 - 2,034 ∴ CE = 46,870
CF = Ai2 - VF = 48,904 - 3,686 ∴ CF = 45,218
CG = Ai2 - VG = 48,904 - 3,990 ∴ CG = 44,914
Topografia I
Profa. Andréa Ritter Jelinek
53
Cálculo do Contra-nivelamento:
Ai3 = CG + RÉG = 44,914 + 3,458 ∴ Ai3 = 48,372
CC = Ai3 - VC = 48,372 - 0,301 ∴ CC = 48,071
Ai4 = CC + RÉC = 48,071 + 2,863 ∴ Ai4 = 50,938
CA = Ai4 - VA = 50,938 - 0,934
∴ CA = 50,004
Verificação do cálculo:
A fórmula geral para verificação da correção do cálculo do nivelamento geométrico
considera que a diferença entre as cotas extremas de um nivelamento é igual à soma das
visadas de ré menos a soma das visadas de vante de mudança:
CF - Ci = ∑ RÉ - ∑ VM
Para o nosso exemplo: 50,004 - 50,000 = 8,978 - 8,974; então 0,004 = 0,004, o que
comprova a correção dos cálculos.
Quando a igualdade acima não é satisfeita, é porque ocorreu um erro altimétrico de
fechamento da poligonal.
No nosso exemplo o erro altimétrico de fechamento foi de 0,004 m ou 4 mm.
O erro tolerável de fechamento é determinada por:
____________
ET = 2.C.√ perímetro(Km)
em que C representa o erro, por quilômetro. No nosso exemplo foi adotado o limite de 5 mm
por quilômetro, sendo que o erro máximo tolerável em 0,24 Km nivelados será de :
____
ET = 2.5 mm.√ 0,24 = 4,8 mm
Ou seja, o erro obtido está dentro do erro tolerável.
Desde que admissível, o erro total é distribuído uniformemente ao longo da poligonal,
por meio da correção, em cada visada de ré, do erro total dividido pelo número de estações do
nível.
Correção:
Para estação 1 : 1/4.E = 1/4.0,004 = 0,001
Topografia I
Profa. Andréa Ritter Jelinek
54
Para estação 2 : 2/4.E = 2/4.0,004 = 0,002
Para estação 3 : 3/4.E = 3/4.0,004 = 0,003
Para estação 4 : 4/4.E = 4/4.0,004 = 0,004
Finalmente, calculam-se as cotas compensadas, pela seguinte fórmula:
COTA CORRIGIDA = COTA ± (CORREÇÃO)
2.2. Perfis longitudinais
O Perfil longitudinal com exagero de 10 vezes é a maneira de realizar a representação
gráfica de um levantamento altimétrico, como se pode observar na fig. 3.5.
Figura 3.5
Topografia I
Profa. Andréa Ritter Jelinek
55
2.3. Cálculo do greide em um perfil de nivelamento
Greide é a linha que acompanha o perfil, dotada de uma certa declividade, e que
mostra o quanto o solo deve ser cortado ou aterrado.
Cota vermelha (CV): distância vertical entre um ponto qualquer do greide e um ponto
correspondente no terreno. Pode ser positiva (aterro) ou negativa (corte).
Ponto de passagem: quando o ponto do greide coincide com o ponto do terreno, não
havendo corte ou aterro (ponto C).
Declividade do Greide:
d = COTA MAIOR – COTA MENOR
DH
d(%) = DN . 100
DH
Figura 3.6
2.4. Vinculação à rede altimétrica
Superfície de nível ou equipotencial é a superfície ao longo da qual a força da
gravidade realiza um trabalho nulo; as superfícies equipotenciais da Terra são, em todos os
seus pontos, normais à vertical do lugar. A superfície equipotencial de nível zero, considerada
como superfície de referência, é a superfície equipotencial do nível médio dos mares,
prolongada através dos continentes, ou seja, é a superfície geoidal.
Designa-se por altitude a altura de um ponto do terreno em relação à superfície de
nível médio dos mares e por cota a altura do ponto em relação a um plano horizontal arbitrário.
Sendo assim, quando a referência de nível é uma superfície qualquer, diz-se que o nível é
aparente. O nível é dito verdadeiro, quando o nível médio do mar é a referência.
Topografia I
Profa. Andréa Ritter Jelinek
56
3. Nivelamento Trigonométrico
O nivelamento trigonométrico é baseado na resolução de um triângulo retângulo. Neste
nivelamento, a diferença de nível é determinada de forma indireta, por meio de resoluções de
triângulos situados em planos verticais, que passam pelos pontos cuja diferença de nível se
calcula. A precisão é menor quando comparado ao nivelamento geométrico, da ordem de
alguns decímetros, em contrapartida, tem um rendimento maior, ou seja, um avanço rápido.
Os ângulos de inclinação do terreno são medidos com o emprego do teodolito.
O nivelamento trigonométrico é empregado quando se trata de determinar a diferença
de nível entre dois pontos acessíveis, separados por grande distância, ou quando se tem um
ponto acessível e outros inacessíveis. Nestes casos, aplica-se o processo de interseção
conjugado com resoluções trigonométricas. Neste caso, para medir as distâncias verticais,
conta-se com o auxílio da mira.
Determinação da diferença de nível
O nivelamento trigonométrico baseia-se no valor da tangente do ângulo de inclinação
do terreno, pois o valor desta função trigonométrica representa sempre a diferença de nível por
metro de distância horizontal medida no terreno, entre os pontos considerados.
Assim, determinando a distância horizontal (DH) entre os pontos em estudo e o ângulo
de inclinação do terreno entre eles (α), a diferença de nível (DN) é calculada aplicando-se a
seguinte fórmula:
DN = DH.tg α, deduzida da figura 3.7.
tg α = BB’ / AB’ ∴ tg α = DN / DH ∴ DN = DH.tg α
Desejando-se determinar a diferença de nível existente entre os pontos topográficos A
e B do perfil do terreno representado na figura 3.8, procede-se da seguinte maneira:
onde:
Z é o ângulo zenital;
i é o ângulo vertical;
hi é a medida do centro geométrico da luneta até o ponto topográfico;
FM é a leitura na mira;
DN é a diferença de nível entre os pontos A e B; e
DH é a distância horizontal entre os pontos A e B.
Topografia I
Profa. Andréa Ritter Jelinek
57
Com o teodolito estacionado em A, visa-se a mira colocada verticalmente em B, medese a altura onde o retículo horizontal da luneta intercepta a mira e o ângulo vertical da linha de
visada.
Figura 3.7
Figura 3.8
Topografia I
Profa. Andréa Ritter Jelinek
58
O ângulo vertical pode ser a partir do zênite até a linha de visada, quando o teodolito
tiver o seu limbo vertical zerado no zênite; ou então do horizonte até a linha de visada, quando
o teodolito tiver o seu limbo vertical zerado no horizonte.
Os teodolitos mais modernos, em sua maioria, são zerados no zênite, e a medida dos
ângulos verticais é dita “ângulo zenital”.
Da fig. 3.8 deduz-se:
DNAB + FM = hi + DH.tg i
ou
DNAB = DH.tg i + hi - FM
no caso do teodolito medir ângulos zenitais:
DNAB = DH.cotg Z + hi - FM, sendo que i = 90º - Z.
Devido à substituição do nível verdadeiro pelo nível aparente, quando se realiza um
nivelamento, conforme já foi visto, ocorre um erro devido à curvatura da Terra e refração
atmosférica. A correção a ser feita nas medidas realizadas, conforme já foi mostrado, é de:
C = 0,068.DH2(Km)
Sendo assim, a fórmula do cálculo da diferença de nível entre dois pontos no
nivelamento trigonométrico passa a ser a seguinte:
DNAB = DH.cotg Z + hi - FM + C
Porém, nas visadas curtas, até 250 metros, podemos desprezar as correções da
curvatura e refração.
Nivelamento Trigonométrico de poligonais e outras aplicações
A planilha abaixo contém as observações de campo de um nivelamento trigonométrico
efetuado na poligonal aberta ABCD. As cotas de A e D são conhecidas, sendo 150 m e 135,28
m, respectivamente. O objetivo é calcular as cotas compensadas dos vértices B e C.
Topografia I
Profa. Andréa Ritter Jelinek
59
Planilha:
EST
PV
Z
A
B
B
A
C
B
D
C
92º14’00”
87º52’00”
91º54’00”
88º16’00”
87º23’00”
92º41’00”
C
D
DH
(m)
524,35
524,35
732,46
732,46
631,24
631,24
hi
(m)
1,48
1,52
1,52
1,50
1,50
1,52
FM
(m)
1,000
1,000
1,000
0,000
1,000
1,000
C
(m)
0,02
0,02
0,04
0,04
0,03
0,03
DN
DNMED COTA COR.
COTA
(m)
(m)
(m) COM. (m)
-19,94 -20,01
150,00
20,07
129,99 -0,05
129,94
-23,73 -23,71
23,70
106,28 -0,13
106,15
29,37 29,20
-29,03
135,48 -0,20
135,28
Cálculo da correção devido ao erro de curvatura e refração:
C (m) = 0,068.DH2 (Km)
C = 0,068.(0,52435)2 = 0,01869 ≅ 0,02
C = 0,068.(0,73246)2 = 0,036 ≅ 0,04
C = 0,068.(0,63124)2 = 0,027 ≅ 0,03
Cálculo da diferença de nível:
DNAB = DHAB.cotg Z + hi - FM + C
DNAB = 524,35.(1 / tg 92º 14’) + 1,48 - 1,000 + 0,02 = -19,94
DNBA = 524,35.(1 / tg 87º 52’) + 1,52 - 1,000 + 0,02 = 20,07
DNBC = 732,46.(1 / tg 91º 54’) + 1,52 - 1,000 + 0,04 = -23,73
DNCB = 732,46.(1 / tg 88º 16’) + 1,50 - 0,000 + 0,04 = 23,70
DNCD = 631,24.(1 / tg 87º 23’) + 1,50 - 1,000 + 0,03 = 29,37
DNDC = 631,24.(1 / tg 92º 41’) + 1,52 - 1,000 + 0,03 = -29,03
Cálculo da diferença de nível média:
DNAB = -19,94 e DNBA = 20,07; então DNm = -20,01
DNBC = -23,73 e DNCB = 23,70; então DNm = -23,71
DNCD = 29,37 e DNDC = -29,03; então DNm = 29,20
Observa-se que o sinal é resultante das visadas das diferenças de nível em um mesmo
sentido, ou seja, adotam-se os sinais das DNAB, DNBC e DNCD; e é feita a média aritmética dos
valores.
Topografia I
Profa. Andréa Ritter Jelinek
60
Cálculo das cotas:
CB = CA + DNAB = 150,00 + (-20,01) ∴ CB = 129,99
CC = CB + DNBC = 129,99 + (-23,71) ∴ CC = 106,28
CD = CC + DNCD = 106,28 + 29,20 ∴ CD = 135,48
Cálculo do erro e correção:
ε = cota calculada - cota conhecida
ε = 135,48 - 135,28 = 0,20
n
i
i=1
i=1
C = (-ε / ∑ Li ) .∑ Li
onde:
Li é a soma dos lados; e
n é o número de vértices.
C1 = [-(0,20) / 1888,05].524,35 = -0,05
C2 = [-(0,20) / 1888,05].(524,35 + 732,46) = -0,13
C3 = [-(0,20) / 1888,05].(524,35 + 732,46 + 631,24) = -0,20
Cálculo das cotas compensadas:
COTA COMPENSADA = COTA + CORREÇÃO
CB = 129,99 - 0,05 = 129,94
CC = 106,28 - 0,13 = 106, 15
CD = 135,48 - 0,20 = 135,28
Determinação da cota de um ponto inacessível
Considerando-se a figura 3.9, seja P o ponto cuja cota queremos determinar, com o
auxílio de uma base AB. Com o teodolito medimos os ângulos horizontais a e b e os ângulos
zenitais Z1, Z2 e Z3.
Os comprimentos D1 e D2 são obtidos das relações:
DHAP DHBP
=
=
sen γ sen β sen α
DHAB
Topografia I
Profa. Andréa Ritter Jelinek
61
As diferenças de nível serão obtidas pelas seguintes fórmulas:
DN = DH.cotg Z – FM + hi
DNAB = DHAB.cotg Z3 – FM + hi
DNAP = DHAP.cotg Z1 – FM + hi
(FM = 0,000)
DNBP = DHBP.cotg Z2 – FM + hi
(FM = 0,000)
Figura 3.9
Correções a serem feitas:
DNAB inferida = DNmaior – DNmenor
ERRO = │DNAB inferida│ - │DNAB calculada│
CORREÇÃO = erro / 2 = x
DNmaior – x
DNmenor – x
O cálculo das cotas dos pontos B e P, em função da cota de A, que é conhecida, é feito
da seguinte maneira:
CB = CA + DNAB
Topografia I
Profa. Andréa Ritter Jelinek
62
CP = CA + DNAP