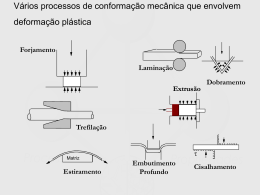
CAPÍTULO VII – RESISTÊNCIA DOS MATERIAIS
Cálculo de deformações de vigas e pilares
Utilização em madeiras
Juntas de dilatação
Revisão Geral – Mecânica
Conceitos Básicos
Força
Grandeza capaz de provocar movimento, alterar o estado de movimento, alterar o estado de
tensão ou provocar deformação em um corpo.
Força:
Unidades:
N – newton
kN – kilonewton
kgf – kilograma-força
Equivalência:
1 kN = 103 N = 98,1 kgf (≅102 kgf)
Para recordar Æ Leis de Newton:
1ª Lei de Newton ou Princípio da Inércia
Todo corpo continua no estado de repouso ou de movimento retilíneo uniforme, a menos que
seja obrigado a mudá-lo por forças a ele aplicadas.
r r
r
Fr = 0 ⇔ v = constante (Repouso ou MRU)
Equilíbrio
2ª Lei de Newton ou Princípio Fundamental
A resultante das forças que agem em corpo é igual ao produto de sua massa pela aceleração
adquirida.
59
PDF created with pdfFactory trial version www.pdffactory.com
r
r
Fr = m.γ
3ª Lei de Newton ou Lei da Ação e Reação
Para toda força aplicada, existe outra de mesmo módulo, mesma direção e sentido oposto.
Ação das forças
Forças Externas : Deformação
Forças internas
- Oposição à ação de forças externas (Resistência) Æ Tensão
- Recuperação da forma original quando cessa força externa (Elasticidade)
Elasticidade e Plasticidade
Elástico
Um corpo é dito elástico quando cessada a aplicação da força, este retornar ao estado inicial
Exemplos: Aço, borracha, madeira
Obs: A elasticidade ocorre dentro de determinados limites
Plástico
Um corpo é dito plástico quando cessada a aplicação da força, o mesmo permanecer em sua
forma atual.
Ex: Chumbo e argila
Todo corpo sujeito à força externa sofre deformação.
As deformações lineares que ocorrem na tração e na compressão são expressas em função da
Variação de Comprimento (∆L) e do Comprimento Original (L).
As deformações podem ser Longitudinais ou Laterais.
Considerações sobre elasticidade e plasticidade
A maioria dos materiais apresenta as duas características, dependendo dos esforços aos quais
estão submetidos, atuando como elásticos até certo limite e depois como plásticos.
Não existe material perfeitamente elástico. Sempre permanecerá uma deformação residual
(Deformação Permanente ou Residual)
Na Figura 53 é mostrada a seqüência de uma aplicação de força de tração e na Figura 54 é
mostrada a seqüência de uma aplicação de duas forças de compressão.
60
PDF created with pdfFactory trial version www.pdffactory.com
1Dada
uma
barra
de 2
Observa-se
comprimento L, aplica-se uma deformação ∆L
força F.
uma 3- Cessada a força o corpo
retorna à forma original.
Figura 53: Aplicação de uma força de tração em uma barra. Fonte: FARIA JÚNIOR (2008).
Modificado.
1- Dada uma
comprimento L,
duas forças F.
barra de 2
Observam-se
aplicam-se deformações ∆L.
duas 3- Cessadas as forças o corpo
retorna à forma original.
Figura 54: Aplicação de duas forças de compressão em uma barra. Fonte: FARIA JÚNIOR (2008).
Modificado.
Lei de HOOKE
As tensões desenvolvidas e suas deformações específicas conseqüentes são proporcionais
enquanto não se ultrapassa o limite elástico do material. Em linhas gerais, a deformação é proporcional
à tensão (ε ∝ σ) (Figura 55), sendo considerado a padronização da deformação de um corpo sólido
para cada 1kgf de aumento na carga (esforço externo) ou para cada 1 kgf/cm2 de aumento na tensão.
61
PDF created with pdfFactory trial version www.pdffactory.com
σ
=E
ε
Onde:
σ= tensão normal
ε=deformação específica (relativa)
E= Módulo de elasticidade longitudinal
(constante elástica do material)
•
•
ε (Deformação relativa)
ε = ∆L/L ou (x 100) = %
Figura 55: Diagrama tensão-deformação.
•
•
•
•
•
E=1/ ∝ (módulo elasticidade) – Valor
da tensão imáginária de tração
(kgf/cm2) capaz de duplicar o
comprimento original do corpo sólido
E=tgθ
E=cat op/cat ad
E= σ/ε
σ =E. ε
Figura 56: Módulo de elasticidade de Young.
62
PDF created with pdfFactory trial version www.pdffactory.com
•
•
E1>E2
ε1< ε2
Figura 57: Exemplo de deformações com 2 tipos de materiais. Fonte: FARIA JÚNIOR (2008).
Modificado.
A Tabela 14 demonstra o módulo de elasticidade para diferentes tipos de materiais.
Tabela 14: Módulo de elasticidade (E) para diferentes materiais. Modificado de BAETA e
SARTOR (1999).
Material
E (kgf/cm2)
Aço
2.100.000
Ferro Fundido
1.000.000
Concreto
20.000 a 400.000
Alvenaria de Tijolo
20.000 a 200.000
Madeira de Pinho (paralelo à fibra)
1.000.000
Madeira de Pinho (perpendicular à fibra)
3.000
Definições
Corpos dúcteis: Deforma-se bastante antes do rompimento (ductibilidade). Ex: Aço, alumínio
Corpos frágeis: Deforma-se pouco antes do rompimento (fragilidade). Ex: concreto, ferro
fundido.
Concreto não obedece a Lei de Hooke, (proporcionalidade) na compressão.
A Figura 58 demonstra o diagrama de tensão-deformação para materiais dúcteis, com as
respectivas tensões atuantes e as deformações.
63
PDF created with pdfFactory trial version www.pdffactory.com
Figura 58: Diagrama de tensão-deformação (materiais dúcteis). Fonte: KALIL e LEGGERINI
Explicando o Diagrama:
Tensões
σp: Tensão de proporcionalidade
σe: Tensão de escoamento
σR: Tensão de ruptura
Trecho A-B
Indica a proporcionalidade entre σ x ε (material trabalha em regime elástico - lei de Hooke).
Deformações reversíveis.
Trecho B-C
Indica o fim da proporcionalidade Æ regime plástico do material.
As deformações crescem mais rapidamente do que as tensões
Cessado o ensaio Æ pequenas deformações residuais irreversíveis.
Trecho C-D
Patamar de escoamento Æ o material se desorganiza internamente (nível molecular) sem que
se aumente a tensão a que o material é submetido, aumenta grandemente a deformação que ele
apresenta.
Período em que começam a surgir falhas no material (estricções), ficando o mesmo invalidado
para a função resistente.
Trecho D-E
64
PDF created with pdfFactory trial version www.pdffactory.com
Após uma reorganização interna o material continua a resistir à tensão em regime plástico
Grandes e visíveis deformações residuais
Não se admitem estruturas com esta ordem de grandeza para as deformações residuais.
Exemplo de ensaio (comportamento do aço)
A Figura 59 demonstra um ensaio de tração com o aço, com esforços externos até a ruptura.
Assim sendo, por meio dos dados pode-se traça o diagrama tensão-deformação para cada
material.
Legenda: Diagrama Tensão Deformação
Limite de proporcionalidade
Limite de elasticidade
Tensão de escoamento
Ponto de força máxima
Ruptura
Figura 59: Diagrama tensão-deformação para o aço.
Tensão admissível (σadm)
Definição: é a tensão máxima que se permite atingir uma estrutura calculada em regime
elástico. É aquela adotada para que as estruturas possam suportar as cargas externas com segurança.
No caso do aço (Figura 60):
Tensão admissível (σadm) =σF/ υ
Resistência máxima (σmáx)=P/Ao
65
PDF created with pdfFactory trial version www.pdffactory.com
Alongamento total até a ruptura (δ) = ∆Lmáx/Lo
Figura 60: Tensão admissível para o aço. Modificado de KALIL & LEGGERINI
Deformações Longitudinais e Laterais
Longitudinal (Figuras 61 e 62)
a1<a2;
∆L=∆L1+∆L2
Figura 61: Na tração (alongamento), com a variação de comprimento. Modificado de BAÊTA e
SARTOR (1999)
a1>a2;
∆L=∆L1+∆L2
Figura 62: Na compressão (encurtamento), com variação no comprimento. Modificado de BAÊTA e
SARTOR (1999).
66
PDF created with pdfFactory trial version www.pdffactory.com
Lateral (Figuras 63 e 64)
b1>b2;
∆L=∆L1+∆L2
Figura 63: Na tração (alongamento), com variação na largura. Modificado de BAÊTA e SARTOR
(1999).
b1<b2;
∆L=∆L1+∆L2
Figura 64: Na compressão (encurtamento), com variação na largura. Modificado de BAÊTA e
SARTOR (1999).
Com relação à deformação:
A deformação específica longitudinal é proporcional à deformação específica transversal
(limite elástico do material), sendo chamada de Coeficiente de Poisson (µ):
εt
µ=−
ε
Onde:
ε = Deformação específica longitudinal
εt = Deformação específica transversal
µ = Coeficiente de Poisson
67
PDF created with pdfFactory trial version www.pdffactory.com
εt = ∆b = ∆h =∆R → ∆b = εt.bi
bi hi
Ri
∆h = εt.hi  Deformação transversal total
∆R = εt.Ri
Na Figura 65 é demonstrado o cisalhamento (escorregamento relativo) em uma barra, onde os
comprimentos e as larguras antes e após a aplicação da força, permanecem inalterados.
a1=a2;
b1=b2;
Figura 65: Escorregamento relativo ou Deformação angular Modificado de BAÊTA e SARTOR
(1999).
A Deformação angular é definida por:
γ=
∆y
∆x
Onde:
∆y = Variação no eixo y (antes e depois à aplicação
da força)
∆x= Variação no eixo x (antes e depois à aplicação
da força)
A Figura 66 mostra o diagrama de tensão-deformação no caso do cisalhamento.
tg θ=cat op/cat ad
τ/ γ=G (módulo de elasticidade
transversal) no cisalhamento
Lei de Hooke para cisalhamento
τ∝γ
τ=G. γ
Figura 66: Diagrama tensão-deformação (cisalhamento)
68
PDF created with pdfFactory trial version www.pdffactory.com
Para os casos das tensões normais, aplica-se Hooke
Identicamente, pode-se expressar o Escorregamento relativo empregando-se o Módulo de
Elasticidade Transversal (G) e a tensão Cisalhante (τ)
τ=G. γ
Entre (E) e (G) existe uma relação que pode ser expressa com o auxílio do coeficiente de
Poisson (µ):
G=
µ
.E
2( m + 1)
Onde:
G=módulo de elasticidade
Transversal (cisalhamento)
τ = Tensão de corte ou
cisalhamento
Variação do comprimento à dilatação
Aquecimento: Dilatação
Arrefecimento: Contração
Podem causas tensões internas nos materiais, semelhantes aos esforços externos (Tabela 15).
Para evitar essas tensões:
Empregar apoios móveis (pontes)
Juntas de dilatação
Dilatação ou compressão
Em peças estruturais, pode ser calculada por:
∆L=±αt. ∆t.L
Onde:
L= comprimento do elemento estrutural
∆t= variação de temperatura do elemento estrutural
αt=coeficiente de dilatação térmica (variação de comprimento do elemento estrutural para
cada 1oC)
Tabela 15: Valores de αt para diferentes materiais. Modificado de BAÊTA e SARTOR (1999).
Material
αt (oC-1)
Aço
0,000012
Ferro fundido
0,000010
Concreto
0,000010
Alvenaria de tijolo
0,000005
Madeira
0,000003
69
PDF created with pdfFactory trial version www.pdffactory.com
A retração da argamassa pela evaporação tem ação semelhante à variação provocada pela
diminuição de temperatura. Para o concreto simples e armado, a retração deve ser correspondente a
uma queda adicional de 20oC
70