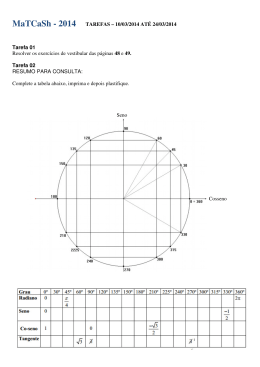
▼
Questão 16
Uma curva em formato espiral, composta por arcos de circunferência, pode ser construída a partir de dois
pontos A e B, que se alternam como centros dos arcos. Esses arcos, por sua vez, são semicircunferências que
concordam sequencialmente nos pontos de transição, como ilustra a figura abaixo, na qual supomos que a
distância entre A e B mede 1cm.
R3
A
R1
B
R2
R4
a) Determine a área da região destacada na figura.
b) Determine o comprimento da curva composta pelos primeiros 20 arcos de circunferência.
Resolução
Considere a seguinte figura:
R3
A
1
1
1
R1
1
B
1
1
1
1
R2
R4
a) A região destacada é formada por 2 semicírculos de raios 3cm e 4cm; assim, sua área, em cm2, é dada por:
1
1
25π
⋅ π ⋅ 42 + ⋅ π ⋅ 32 =
cm2
2
2
2
25π
cm2
2
b) O 1o arco tem raio 1cm; o 2o arco, 2cm; e assim sucessivamente até o 20o arco, cujo raio mede 20cm. O
comprimento da curva, em cm, é:
1
⋅ [2π ⋅ 1 + 2π ⋅ 2 + … + 2π ⋅ 20]
2
= π + 2π + … + 20π
(π + 20π) ⋅ 20
=
= 210π cm
2
Resposta:
Resposta: 210π cm