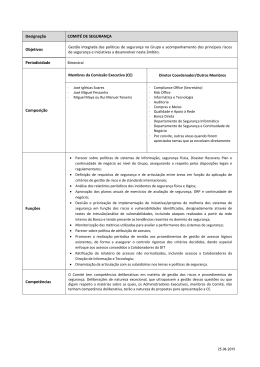
GABARITO COMENTADO FUNDAMENTOS DA MATEMÁTICA I
Professores: Joelson de Araújo e Paulo Vitoriano
Leia com atenção as questões de A a J referentes à Avaliação MPII
módulo II e marque de acordo com os comandos solicitados.
A . O valor numérico da expressão 3ab − 5 a +
4 2
a b − ab 3 , para a = 4 e b = - 3, temos:
5
1) 118/5
2) - 962/5
3) 218/5
4) 142/5
3.4. ( −3 ) − 5 4 +
4 2
3
4 . ( −3 ) − 4. ( −3 ) = 118 (ASSERTIVA 1)
5
5
B. O grau de um polinômio é determinado pelo termo de maior expoente, o grau do polinômio é: 5ax 5 + 2b2 x 3 y −6 −
3 4 5 3a3 x 8
x y +
:
4
5b4
1) 9
2) 15
3) 6
4) 11
Como o grau de um polinômio é dado pelo maior valor obtido através da soma dos expoentes de cada
monômio, assim, o monômio de maior soma de seus expoentes é 9, que corresponde a soma dos
expoentes do 3° monômio −
3 4 5
x y (ASSERTIVA 1)
4
C. O quociente da divisão do polinômio x 4 - 3x 3 + 8x 2 + 2 pelo polinômio x 2 + 2x é:
1) x 2 - 5x + 18
2)
- 36x + 2
3) x 2 + 5x + 18
4) x 2 - 5x + 1
(ASSERTIVA 1)
x4 – 3x + 8x2 + 2 x2 + 2x ‐x4 ‐2x3 x2 – 5x + 18 →Quociente 0 ‐5x3 + 8x2 5x3 + 10x2 0 + 18x2 + 2 ‐ 18X2 – 36X 0 ‐36x2 + 2 D. Para resolvermos um problema de equação do primeiro grau, temos que transcrever o texto em
símbolos matemáticos, depois desenvolver as operações algébricas para determinarmos o valor da
variável. Sendo assim, determine o valor da variável quando temos: o quádruplo de, um número menos
15, é igual ao triplo do mesmo número somado com dois. Esse número é
1) 62.
2) 17.
3) 13.
4) 66.
4(x – 15) = 3x + 2
x = 62
(ASSERTIVA 1)
E. Utilizando um dos métodos de resolução de sistemas de equações do primeiro grau, determine o
⎧ x + 2y = 18
⎩ 3x - 4y = 14
conjunto solução do sistema ⎨
1) S = { ( - 10; - 4 ) }
2) S = { ( 1; 4 ) }
3) S = { ( 10; - 4 ) }
4) S = { ( 10; 4 ) }
Multiplicando a primeira equação por -3 temos;
⎧ − 3x − 6y = − 54
⎨
⎩ 3x -4y = 14 logo,
0 − 10y = −40
x + 2.4 = 18 ⇒ x = 10
(ASSERTIVA 4)
y=4
ASSIM, S = {10;4}
F. Podemos afirmar que o domínio da função f ( x ) =
x+3
x
−1
2
, dentro do conjunto dos números
reais é: 1) D = { x Є R / x = 2 }
2) D = { x Є R / x > 2 }
3) D = { x Є R / x < 2 }
4) D = { x Є R / x > - 2 }
x
−1> 0 ⇒ x − 2 > 0
2
(ASSERTIVA 2)
x > 2, assim, D = {x ∈ R x > 2}
G. Qual dos gráficos abaixo representa uma função, considerando o eixo horizontal sendo o eixo das
abscissas e o eixo vertical sendo o eixo das ordenadas.
1)
2)
3)
4)
Dê acordo com a definição de função, somente o gráfico 3 representa uma função, pois cada
elemento de seu domínio (x) relacionou com somente um elemento de seu conjunto imagem (y).
(ASSERTIVA 3)
H . Observando o gráfico a seguir de uma função do tipo y = ax + b, podemos afirmar que, a função
que melhor representa este gráfico é:
ƒ Como o gráfico intercepta o eixo y em y = 6 temos b= 6. 1) y = - 3x - 4
2) y = 3x + 6
3) y = 3x + 2
4) y = - 3x + 6
ƒ Como a função é decrescente, ou seja a < 0 e o gráfico intercepta o eixo x em x = 2 para x = ‐b/a logo, a = ‐3 (ASSERTIVA 4) y 6 x
2 I . O departamento de tecnologia da informação da UNITINS monitorou os acessos de seus alunos ao
portal (AVA) de interatividade durante alguns dias. Após encerrar esse monitoramento verificou que
os acessos diários por seus acadêmicos podem ser calculados pela função y = - 2x2 + 20x + 150,
conforme o gráfico a seguir. Podemos afirmar que o valor máximo de acessos diários foi de:
Como a < 0, a função define ponto máximo em ACESSOS Yv= ‐∆/4a, como ∆ = b2 – 4.a.c = 1600 1) 100 acessos.
2) 200 acessos.
3) 300 acessos.
4) 400 acessos.
Yv= ‐1600/‐ 8 150 Yv= 200 acessos (ASSERTIVA 2) DIAS
J. Analisando o gráfico da função do 2º grau a seguir, do tipo ax2 + bx + c = 0, podemos afirmar que
os valores dos seus coeficientes e do discriminante são:
y
1) a < 0; b < 0; c < 0 e ∆ = 0
2) a > 0; b < 0; c < 0 e ∆ = 0
3) a < 0; b > 0; c < 0 e ∆ = 0
4) a < 0; b > 0; c < 0 e ∆ > 0
¾
¾
¾
¾
x
Como o gráfico intercepta o eixo de x em um único ponto, temos ∆ = 0
Como a parábola possui concavidade voltada para baixo, temos a < 0
Como o gráfico intercepta o eixo de y abaixo do eixo de x, temos c < 0
Como xv = -b/2a e no gráfico é positivo, temos b > 0
(ASSERTIVA 3)
Moisés de Souza Arantes Neto
Coordenador do Curso de Matemática
UNITINS- EAD