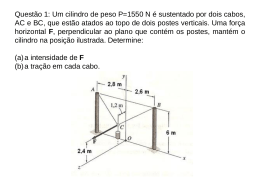
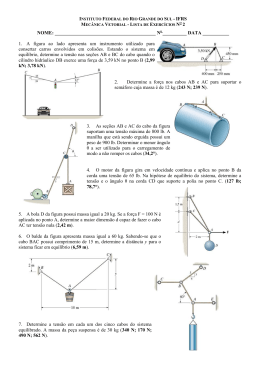
PUC - Goiás
Curso: Engenharia Civil
Disciplina: Mecânica Vetorial
Corpo Docente: Geisa Pires
Plano de Aula
Leitura obrigatória
Mecânica Vetorial para Engenheiros, 5ª edição revisada, Ferdinand P. Beer, E. Russell Johnston, Jr.
Editora Pearson
CAPÍTULO 2 – Estática dos Pontos Materiais
4. Adição de Vetores
1. Introdução
   
PQ Q P
  

 P  Q  Q  ( P)
 

  
P  Q  S  (Q  P)  S
Aqui estudaremos o efeito de forças que atuam em
pontos materiais.
Primeiramente estudaremos forças contidas em um
plano, em seguida estudaremos forças no espaço
(tridimensional)
5. Resultante de Várias Forças Concorrentes
Após somarmos todas as forças que atuam em um
ponto, temos a resultante, ou seja, a força única que
tem o mesmo efeito sobre o ponto de aplicação de
todas as forças.
FORÇAS NO PLANO
2. Forças Sobre um Ponto Material. Resultante
de Duas Forças
6. Decomposição de Uma Força em
Componentes
Força: Ação de um corpo sobre outro corpo.
É obtido pelo caminho inverso de “.5” . Quando

temos uma força R ela pode ser obtida por
componentes separadas que quando somadas

vetorialmente nos dá R .
7. Componentes Cartesianas de Uma Força.
Vetores Unitários.
 Ponto de aplicação, intensidade, direção e
sentido.
Muitas vezes é desejável decompor uma força em
componentes normais entre si. É comum usar o
eixo x e o eixo y para isso. Assim as componentes
são chamadas de componentes cartesianas (Fx e Fy)
 Constata-se que se duas forças atuam em
um ponto, tais podem ser substituídas por
uma única força chamada de força
resultante.
3. Vetores
Vetores: Entes matemáticos que possuem
intensidade, direção e sentido e que se somam de
acordo com a Lei do Paralelogramo.
1


R  F  0
 ( F iˆ  F ˆj )  0
( F )iˆ  ( F ) ˆj  0
F  0
F  0
x
x
y
y
x
y
10. Problemas Relacionaods ao Equilíbrio de
um Ponto Material. Diagrama de Corpo
Livre
Assim:

Fx  Fx iˆ

Fy  Fy ˆj

F  Fx iˆ  Fy ˆj
Nossos problemas são retirados do cotidiano. Um
esquema mostrando as condições físicas do
problema é conhecido como diagrama espacial.
11. Força Definida por Seu Módulo e Dois
Pontos de Sua Linha de Ação
8. Adição de Forças Pela Soma das
Compnentes Cartesianas
Seja a figura a seguir:
Seja a soma vetorial:
   
R  PQS
Rx iˆ  R y ˆj  ( Px iˆ  Py ˆj )  (Qx iˆ  Q y ˆj )  ( S x iˆ  S y ˆj )

R  ( Px  Q x  S x )iˆ  ( Py  Q y  S y ) ˆj
R x  Px  Q x  S x
R y  Py  Q y  S y
R x   Fx
R y   Fy
Então:
9. Equilíbrio de Um Ponto Material
MN  dxiˆ  dyˆj  dzkˆ
Equilíbrio: Quando a resultante de todas as forças
que atuam sobre um ponto material é zero, este
ponto está em equilíbrio.
Ou
Matematicamente
Ou
 F
F  (dxiˆ  dyˆj  dzkˆ)
d


MN
1
 (dxiˆ  dyˆj  dzkˆ)
| MN | d
Lembrando que d é a distância entre M e N.
2
Portanto:
Exercícios
1 – A haste CB exerce no bloco B uma força P
dirigida ao longo da reta CB. Sabendo que P tem
uma componente horizontal de 200 N, determine:
Fdx
d
Fdy
Fy 
d
Fdz
Fz 
d
Fx 
12. Adição de Forças Concorrentes no Espaço
A adição de forças concorrentes no espaço é feita
pelo modo cartesiano:


R  F
R x   Fx
R y   Fy
a) A intensidade da força P. R: 261 N
R z   Fz
b) Sua componente vertical. R: -168 N
Ainda
R 2  Rx2  R y2  Rz2
2 – A tração no cabo AC é de 370 N. Determine as
componentes horizontal e vertical da força exercida
em C. R: -120 N, 350 N
13. Equilíbrio de um Ponto Material no Espaço
Um ponto está em equilíbrio se a força resultante
que atua no ponto é zero.

F  0
3
3 – Dois cabos estão atados em C, onde é aplicada
uma carga. Determine as trações em AC e BC.
6 – A manga A com 7,5 kg desliza sem atrito em
um eixo vertical. Ela está presa por um fio, através
de uma polia sem atrito a um peso de 8,5 kg.
Determine a altura h para que o sistema esteja em
equilíbrio. R: 0, 75 m
R: TAC = 352 N; TBC = 261 N
4 – Duas forças P e Q de intensidade P = 600 N e
Q = 800 N são aplicadas a uma conexão de avião.
Sabendo que a conexão está em equilíbrio,
determine a tração nas barras A e B.
R: TA= 231 N e TB = 577 N
7 – Um caixote de 300 kg deve ser sustentado pelo
arranjo de cordas e polias da figura. Determine o
módulo e a direção da força F que deve ser
aplicada à extremidade da corda.
R: 1070 N
5 – Na figura abaixo, dois cabos estão atados no
ponto A, sujeito a uma carga de 960 N. Sabendo
que P = 640 N, determine a tração em cada cabo.
R: TAB = 600 N e TAC = 344 N
4
8 – O cabo AB, de 19,5 m, está sujeito a uma
tração de 19500 N. Determine as componentes
cartesianas da força aplicada pelo cabo em B.
R: - 9305 N, +16800 N, +3385 N
10 – À barra OA é aplicada uma carga P. Sabendo
que a tração no cabo AB é de 850 N e que a
resultante da carga P e das forças aplicadas pelos
cabos em A deve ter a direção de OA, determine a
tração no cabo AC.
R: 510 N
09 – A fim de remover um caminhão acidentado,
dois cabos são atados em A e puxados por dois
guinchos – B e C. Sabendo que a tração no cabo
AB é de 10 kN, determine as componentes da força
exercida pelo cabo AB no caminhão.
R: - 6, 30kN, + 6, 06kN , + 4,86 kN
5
11 – Um recipiente está suspenso por três cabos, como ilustrado. Determine o peso P do recipiente
sabendo que a tração no cabo AB é de 4 kN.
R: 9,32 kN
12 – Um recipiente está suspenso por três cabos, como ilustrado acima. Determine o peso P do recipiente
sabendo que a tração no cabo AD é de 3,87 kN. (Figura acima)
13 – Tentando cruzar uma superfície gelada e escorregadia, um homem de 90 kg utiliza duas cordas, AB
e AC. Sabendo que a força exercida pela superfície no homem é perpendicular à superfície, determine a
tração em cada corda.
R: TAB = 158,5 N e TAC = 321,5 N
6