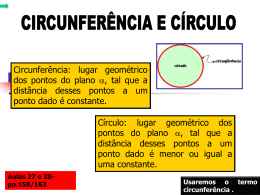
Matemática e suas
Tecnologias - Matemática
Ensino Médio, 3ª Ano
Geometria analítica:
Equações da circunferência
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
INTRODUÇÃO
Neste tópico, estudaremos as equações da
circunferência no plano cartesiano. Antes, porém,
é importante compreender alguns conceitos de
Geometria Plana ou Euclidiana, que veremos a
seguir.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
CIRCUNFERÊNCIA
Corda: distância
(segmento) entre
dois pontos da
circunferência.
Diâmetro = 2r.
O diâmetro é uma
corda que passa pelo
centro
da
circunferência.
Raio (r): distância
do
centro
a
qualquer ponto
da circunferência.
Circunferência
Centro (C)
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
DIFERENÇA ENTRE CÍRCULO E CIRCUNFERÊNCIA
Área do
círculo
Ac = r²
Comprimento da
circunferência
(C = 2r)
Circunferência
não tem área.
Ex.: anel.
Círculo
Ex.: moeda.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
EQUAÇÕES DA CIRCUNFERÊNCIA:
EQUAÇÃO REDUZIDA DA CIRCUNFERÊNCIA
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
Considere
no
plano
cartesiano
uma
circunferência de centro C (a, b), raio r e um
ponto qualquer da circunferência P(x, y), como
mostra a figura a seguir:
y
y
P(x, y)
r
b
Note que, ao localizar o
ponto P(x, y) e o centro
C(a, b), formamos um
triângulo retângulo.
C(a, b)
a
x
x
O raio (r) da
circunferência é a
hipotenusa desse
triângulo retângulo.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
REVENDO O TEOREMA DE PITÁGORAS
Hipotenusa “a”.
É o maior lado
do
triângulo
retângulo.
Cateto “c”.
a
c
b
Cateto “b”.
Teorema de Pitágoras:
a² = b² + c²
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
Na circunferência, temos o triângulo retângulo
de raio r, cateto (x – a) e cateto (y – b). Dessa
forma, ao aplicarmos o Teorema de Pitágoras,
encontramos a equação reduzida da
circunferência.
Pelo Teorema de Pitágoras, temos:
r
(x – a)² + (y – b)² = r²
(y – b)
(x – a)
Equação reduzida da
circunferência.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
RESOLVA AS SITUAÇÕES-PROBLEMA.
S1) Considerando a equação da circunferência
(x - 2)² + (y + 5)² = 16, determine o centro e o raio
dessa circunferência.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
SOLUÇÃO
Vamos comparar a equação reduzida da
circunferência com a equação da situação
proposta.
(x – a)² + (y – b)² = r²
(x – 2)² + (y + 5)² = 16
• - a = -2 . (-1) a = 2
• - b = +5 . (-1) b = -5
• r² = 16 r = 4
Conclusão
Essa circunferência possui C(2, -5) e r = 4.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
RESOLVA AS SITUAÇÕES-PROBLEMA.
S2) Escreva a equação reduzida da circunferência
que tem centro C(-3, 6) e raio r = 5.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
SOLUÇÃO
A equação reduzida da circunferência é da forma
(x – a)² + (y – b)² = r². Como o centro é C(-3, 6) e o
raio é r = 5, vamos substituir os valores do centro
e do raio nessa equação.
(x – a)² + (y – b)² = r²
(x – (-3))² + (y – 6)² = 5²
(x + 3)² + (y – 6)² = 25
Conclusão
A equação reduzida da circunferência é (x + 3)² + (y – 6)² = 25.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
EQUAÇÕES DA CIRCUNFERÊNCIA:
EQUAÇÃO GERAL DA CIRCUNFERÊNCIA
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
Antes de determinarmos a equação geral da
circunferência, vamos relembrar a regra dos
produtos notáveis: o quadrado da soma e o
quadrado da diferença de dois termos.
(a – b)² = a² - 2ab + b²
Quadrado da
diferença
de
dois termos.
(a + b)² = a² + 2ab + b²
Quadrado da
soma de dois
termos.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
EXEMPLO: Calcule os produtos notáveis a seguir.
a) (a – 2)²
= a² - 2. a . 2 + 2² = a² - 4a + 4.
b) (b + 3)²
= b² + 2 . b . 3 + 3² = b² + 6b + 9.
RESPOSTAS
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
Para determinar a equação geral da
circunferência, utilizaremos a equação reduzida
da circunferência (x – a)² + (y – b)² = r² e
resolveremos os produtos notáveis: quadrado da
diferença de dois termos.
(x – a)² + (y – b)² = r²
x² - 2ax + a² + y² - 2by + b² = r²
Equação geral da
circunferência.
x² + y² - 2ax - 2by + a² + b² - r² = 0
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
RESOLVA AS SITUAÇÕES-PROBLEMA.
S1) Escreva a equação geral da circunferência,
que tem centro C(-1, 2) e raio r = 3.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
SOLUÇÃO
S1) Vamos utilizar a equação reduzida e substituir
o centro C(-1, 2) e o raio r = 3. Em seguida,
vamos resolver os produtos notáveis.
(x – a)² + (y – b)² = r²
Equação geral da
circunferência.
(x – (-1))² + (y – 2)² = (3)²
(x + 1)² + (y – 2)² = (3)²
Conclusão:
x² + 2x + 1 + y² – 4y + 4 = 3
x² + y² + 2x – 4y+ 4 + 1 - 3 = 0 x² + y² + 2x – 4y+ 2 = 0
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
RESOLVA AS SITUAÇÕES-PROBLEMA.
S2) A equação x² + y² - 6x + 8y + 5 = 0 representa
uma circunferência. Determine as coordenadas
do centro e o raio.
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
SOLUÇÃO
S2) Vamos comparar a equação da situação com a
equação geral da circunferência.
x² + y² - 2ax - 2by + a² + b² - r² = 0
x² + y² - 6x + 8y + 5 = 0
a² + b² - r² = 5
-2a = -6 . (-1) a = 3
(3)² + (-4)² - r² = 5
9 + 16 – r² = 5
-2b = 8  b = -4
r² = 20  r = 20=25
Conclusão C(3, -4) e r = 25 .
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
EXERCÍCIOS DE FIXAÇÃO
1º) Determine as coordenadas do centro C(a, b)
e o raio r das circunferências de equação:
RESPOSTAS
a) ( x – 5) ² + (y + 6) ² = 8
b) x ² + (y – 4) ² = 25
C(5, -6) e r = 8=22
C(0, 4) e r = 5
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
EXERCÍCIOS DE FIXAÇÃO
2º) Determine a equação reduzida da
circunferência de centro (2, 5) e raio igual a
3.
RESPOSTA
(x – 2)² + (y – 5)² = 9
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
EXERCÍCIOS DE FIXAÇÃO
3º) Escreva a equação geral da circunferência de
centro C (-1, -2) e de raio 4.
RESPOSTA
x² + y² + 2x + 4y – 11 = 0
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
EXERCÍCIOS DE FIXAÇÃO
4º) Verifique entre os pontos A(-1, 3), B(-1, 2), C(2, 3) e D(7, 2) quais pertencem à circunferência
de equação (x – 3)² + (y + 1)² = 25.
RESPOSTA
BeD
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
EXERCÍCIOS DE FIXAÇÃO
5º) Escreva a equação geral da circunferência,
representada pelo gráfico a seguir.
y
RESPOSTA
0
x
x² + y² - 64 = 0
-8
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
PROBLEMAS DE VESTIBULARES
1º) (FEI-SP) Quais são o centro e o raio da
circunferência de equação x² + y² = 2(x – y) + 1?
RESPOSTA
C(1, -1) e r = 3
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
PROBLEMAS DE VESTIBULARES
2º) (UFRS) A equação da circunferência de
diâmetro AB , com A (3, 1) e B (1, -3), é:
a) x2 + y2 + 4x – 2y – 15 = 0
b) x2 + y2 – 4x + 2y – 15 = 0
c) x2 + y2 – 4x + 2y = 0
d) x2 + y2 + 4x + 2y = 0
e) x2 + y2 – 2x + 4y = 0
RESPOSTA
MATEMÁTICA, 3º Ano
Geometria analítica: equações da circunferência
REFERÊNCIAS BIBLIOGRÁFICAS
DANTE, Luiz Roberto. Matemática, volume único. 1ª edição. Ática. São Paulo, 2005.
 IEZZI, Gelson... [et al], Matemática: ciência e aplicações, 3ª série, Ensino Médio.
Atual, São Paulo, 2004.
 GUELLI, Oscar. Matemática, volume único. 1ª edição. Ática. São Paulo, 2003.
PAIVA, Manoel. Matemática, volume único. 1ª edição, Moderna. São Paulo, 1999.