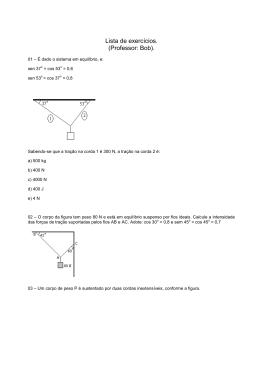
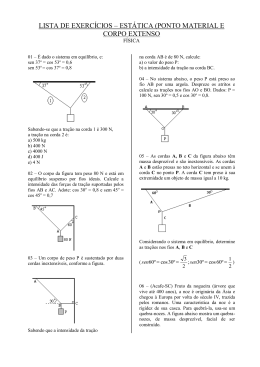
P3 – Física 3º BIMESTRE
Instruções:
•
Entregar somente a resolução da lista de exercícios em folha sulfite (não
precisa entregar, nem imprimir os enunciados). Não esqueça de colocar
“NOME”, “NÚMERO DE MATRÍCULA” e “SEDE”.
•
Extrair os dados do enunciado com suas respectivas unidades. Caso necessário
altere as unidades antes de efetuar os cálculos.
•
Encontre uma fórmula que resolva o problema e então substitua os valores.
•
Efetue os cálculos e deixe de maneira explícita sua resposta (escreva a resposta
a caneta, circule, etc.)
EXERCÍCIOS:
1.
O corpo abaixo está em equilíbrio estático, determine o valor da tração na
corda 1 e na corda 2. (Dados: m = 20 kg, sen β = 0,5 e cos β = 0,8)
2.
O corpo abaixo está em equilíbrio estático, determine o valor da tração na
corda 1 e na corda 2. (Dados: m = 30 kg, sen α = 0,8 e cos α = 0,5, sen β = 0,5 e cos β =
0,8)
3.
A barra abaixo é homogênea e de massa desprezível com comprimento de 1,0
m. No ponto A é colocado um corpo de massa de 5,0 kg e está a uma distância de 30
cm do ponto de apoio. Afim de manter a barra em equilíbrio, qual deve ser o valor da
massa a ser colocada no ponto B?
4.
A barra abaixo é homogênea e com 25,0 kg de massa com comprimento de 6,0
m. Um bloco de massa de 5,0 kg é colocado a 2,0 m do ponto B. Qual é a força de
reação no ponto A e no ponto B? Considere g = 10 m/s2.
5.
O corpo A está ligado a outro corpo B através de um fio ideal passando por uma
polia. Para que o sistema fique em equilíbrio estático qual deve ser o valor do
coeficiente de atrito na superfície de apoio e corpo A?
6.
Aplicando uma força F de intensidade de 1000 N em uma extremidade da
corda, qual é o valor da força peso para que o sistema permaneça em equilíbrio
estático?
7.
Considere uma estrela em torno da qual gravita um conjunto de planetas. De
acordo com a 1ª lei de Kepler:
a) Todos os planetas gravitam em órbitas circulares.
b) Todos os planetas gravitam em órbitas elípticas em cujo centro está a estrela.
c) As órbitas são elípticas, ocupando a estrela um dos focos da elipse; eventualmente,
a órbita pode ser circular, ocupando a estrela o centro da circunferência.
d) A órbita dos planetas não pode ser circular.
e) A órbita dos planetas pode ter a forma de qualquer curva fechada.
8.
Tendo em vista as Leis de Kepler sobre os movimentos dos planetas, pode-se
afirmar que:
a)
a velocidade de um planeta, em sua órbita, aumenta à medida que ele se afasta
do sol;
b)
o período de revolução de um planeta é tanto maior quanto maior for sua
distância do sol;
c)
o período de revolução de um planeta é tanto menor quanto maior for sua
massa;
d)
o período de rotação de um planeta, em torno de seu eixo, é tanto maior
quanto maior for seu o período de revolução;
e)
o sol se encontra situado exatamente no centro da órbita elíptica descrita por
um dado planeta.
9.
Por que o período de translação do planeta Mercúrio em torno do Sol é menor
que o da Terra?
10.
Marte tem dois satélites: Fobos, que se move em órbita circular de raio 10000
km e período 3,0 . 104 s, e Deimos, que tem órbita circular de raio 24000 km.
Determine o período de Deimos.
11.
Dada a massa de um planeta X de 8,0 . 104 kg e a de um planeta Y com 2,0 . 105
kg, determine a força de atração gravitacional sabendo que a distância que os separa é
de 4,0 . 103 km. (G = 6,67 . 10-11 N.m2/kg2)
12.
Sabendo que a força de atração gravitacional entre o Sol e um planeta Z
qualquer vale F, determine o valor da nova força caso a massa do Sol seja dobrada e a
do planeta seja triplicada e a distância que os separa seja reduzida à metade.
13.
Determine o campo gravitacional de um planeta A o qual possui massa de 5,0 .
15
10 kg e raio de curvatura igual a 3,0 105 km. (G = 6,67 . 10-11 N.m2/kg2)
14.
Com relação ao exercício anterior, calcule o campo gravitacional a uma
distância de 3,5 . 105 km do planeta.
15.
Um corpo está sob uma plataforma de 1,5 m de altura e está com velocidade
de 30 m/s. Determine o tempo de queda e qual a distância, em relação ao início da
plataforma, que o corpo atingirá o solo, despreze qualquer forma de atrito: (g = 10
m/s2)
16.
Um canhão dispara um projétil de 10 kg de massa com uma velocidade de 200
m/s com um ângulo de incidência de 60 º em relação a horizontal. Desprezando o
atrito com o ar, calcule o tempo de subida, a altura máxima atingida, o tempo total de
queda e o alcance máximo. (sen 60º = 0,8 , cos 60º = 0,5)
17.
Um arqueiro dispara uma flecha com velocidade inicial de 10 m/s com uma
inclinação de 45º, determine a máxima distância atingida pela flecha. Despreze a
resistência do ar e sen 45º = cos 45º = 0,7.