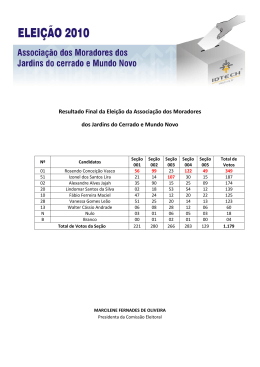
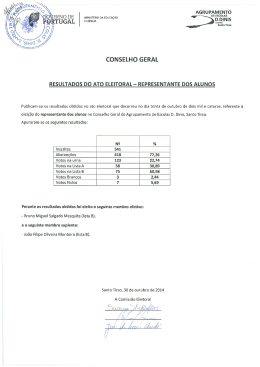
▼
Questão 4
Os alunos de uma classe foram consultados sobre quatro possibilidades diferentes de horário para o exame
final da disciplina (possibilidades A, B, C e D). Cada aluno ordenou sua preferência da 1a à 4 a escolha (a 1a é
a mais desejada, e a 4a a menos desejada). A apuração dos resultados dessa consulta mostrou que foram escolhidas apenas 9 ordenações diferentes, dentre as 24 possíveis. A tabela indica os resultados da consulta com os
dados agrupados.
Número de votos
1a escolha
2a escolha
3a escolha
4a escolha
3
A
B
C
D
4
A
B
D
C
7
A
C
B
D
8
B
C
D
A
2
B
A
C
D
5
B
C
A
D
8
C
D
B
A
2
C
A
D
B
11
D
C
A
B
Exemplo: do total de 50 alunos, 3 preferem A à B, B à C e C à D (primeira coluna da tabela).
a) Usando os dados da tabela, determine o horário vencedor, e com que porcentagem de votos, em uma
eleição majoritária simples.
Definição: eleição majoritária simples é aquela em que se leva em consideração apenas a 1a escolha de cada
eleitor.
b) Admita, agora, que são atribuídos peso quatro (4 pontos) à 1a escolha de cada aluno, três (3 pontos) à 2a
escolha, dois (2 pontos) à 3a escolha e um (1 ponto) à 4a escolha.
Dada a matriz V1 × 9 = [3 4 7 8 2 5 8 2 11], determine a matriz P9 × 4 de forma que V1 × 9 ⋅ P9 × 4 resulte
a matriz T1 × 4 = [A B C D] do total de pontos dos horários A, B, C e D. Em seguida, ordene a classificação
dos quatro horários, do que obteve mais pontos para o que obteve menos pontos.
Resolução
a) Temos do enunciado que, na eleição majoritária simples, só importa a 1a escolha. Portanto temos a tabela:
3
A
4
A
7
A
8
B
2
B
5
B
8
C
2 11
C D
Realizando a soma das escolhas, temos:
A: 14 votos
B: 15 votos
Logo, B vence.
C: 10 votos
D: 11 votos
De um total de 50 votos, 15 foram para B, portanto teríamos uma vitória com
15
= 30% dos votos.
50
Resposta: B é o horário vencedor; 30% dos votos.
b) Temos uma matriz V1 × 9 com o número de pessoas que votou para cada sequência de escolhas, por exemplo:
O primeiro elemento (3) representa as 3 pessoas que fizeram: 1a escolha — A, 2a escolha — B, 3a escolha —
C, 4a escolha — D. Atribuem-se, assim, 4 pontos por pessoa para A, 3 pontos por pessoa para B, 2 pontos
por pessoa para C e 1 ponto por pessoa para D.
Assim sendo, a matriz P9 × 4 deve conter os pontos que foram dados para cada horário por cada grupo. Sendo
assim:
P9 × 4
⎤ 44 33 21 12 ⎤
⎥4 2 3 1 ⎥
⎥1 4 3 2 ⎥
= 3 4 2 1
⎥ 21 42 34 13 ⎥
⎥3 1 4 2 ⎥
⎦2 1 3 4 ⎦
↑ ↑ ↑ ↑
A B C D
Então:
V1 × 9 ⋅ P9 × 4 = [116 124 147 113]
Portanto a classificação pedida é:
1o: C
2o: B
3o: A
4o: D