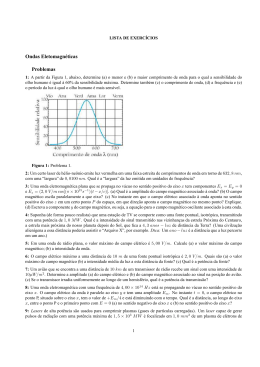
Física III – 2008 - Lista de Exercícios Cap. 33
(01) Usando o Princípio de Fermat, demonstre a Lei de
Snell da refração.
(02) Um raio de luz que viajava inicialmente no ar incide
em uma substância transparente fazendo um ângulo de
58º com a normal. Os raios refletido e refratado são
mutuamente perpendiculares. (a) Qual é o índice de
refração da substância transparente? (b) Qual o ângulo
crítico para reflexão interna total nesta substância?
(03) O ângulo crítico para reflexão interna tortal em uma
substância é 45º. Qual o ângulo de polarização para est
substância?
(04) Duas cordas muito longas, bem esticadas, de
densidades lineares diferentes µ1 e µ2, esão ligadas
uma à outra. Toma-se a posição de equilíbrio como eixo
x e a origem O no ponto de junção, sendo y o
deslocamento transversal da corda. Uma onda
harmônica progressiva viajando na corda 1 (x<0), incide
sobre o ponto de junção, fazendo-o oscilar com
freqüência angular ω. Isto produz na corda 2 (x>0) uma
onda progressiva de mesma freqüência (onda
transmitida) e dá origem, na corda 1, a uma onda que
viaja em sentido contrário (onda refletida). Dada a onda
incidente yi, de amplitude A1, obtenha a amplitude de
reflexão ρ =B1/A1 (onde B1 é amplitude da onda refletida)
e a amplitude de transmissão τ=A2/A1 (onde A2 é a
amplitude da onda transmitida) em função das
velocidades de propagação das ondas nas cordas (v1 e
v2). Para resolver o problema imponha as condições de
contorno apropriadas, explicando cada uma das
passagens realizadas. Discuta o sinal de ρ.
(05) Duas placas polarizadoras estão posicionadas com
os eixos de transmissão cruzados, o que impede a luz
de atravessar o conjunto. Uma terceira placa é inserida
entre as duas. O eixo de transmissão da terceira placa
faz um ângulo θ com o eixo de transmissão da primeira.
Um feixe de luz não-polarizada de intensidade I0 incide
na primeira placa. Determine a intensidade da luz
transmitida pelo novo conjunto para θ=45º e 30º.
Prob. 04
1
(07) (a) Use o resultado do problema 75 do livro-texto
para determinar a relação entre a intensidade da luz
transmitida e a intensidade da luz incidente em uma
pilha de N placas de vidro paralelas no caso de
incidência normal. (b) Determine esta relação para 3
placas de vidro com n=1,5. (c) Quantas placas de vidro
com n=1,5 são necessárias para que a intensidade da
luz transmitida seja igual a 10% da intensidade da luz
incidente?
(08) Um nadador no fundo de uma piscina de 3 m de
profundidade olha para cima e vê um círculo luminoso.
Se o índice de refração da água da piscina é n=1,33,
determine o raio do círculo.
(09) Um raio de luz incide perpendicularmente em uma
placa de vidro com um índice de refração n=1,5. O raio
é refletido nas duas superfícies da placa. Qual a
porcentagem da luz incidente que consegue atravessar
a placa?
(10) Um raio luminoso incide em um bloco retangular
feito de vidro (n=1,5) que está quase totalmente
submerso em água (n=1,33) (v.figura). (a) Determine o
maior ângulo θ para o qual ocorre reflexão interna total
no ponto P. (b) Haveria reflexão interna total no ponto P
para o valor de θ calculado no item (a) se o bloco fosse
retirado da água? Explique.
(11) A figura abaixo mostra um raio de luz incidindo em
uma placa de vidro de espessura d e índice de refração
n. (a) Determine o ângulo de incidência para que a
distância entre os raios refletidos na superfície superior
e inferior da placa de vidro seja máxima. (b) Qual será o
valor deste ângulo de incidência se o índice de refração
for 1,6? Qual será a distância entre os dois raios se a
espessura da placa for de 4 cm?
y
Prob. 10
A1
B1
(06) O mesmo conjunto do problema 05 é usado (3
placas de vidro). Determine a intensidade da luz
transmitida em função de θ (v. definição deste ângulo no
problema 05). Mostre que a intensidade é máxima
quando θ=45º.
A2
O
2
x
Prob. 11