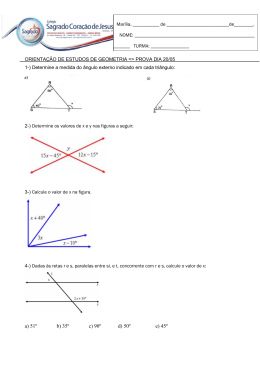
Questão 1
Seja f a função real dada por f(x) = ax£ + bx + c, com a > 0.
Determine a, b e c sabendo que as raízes da equação | f (x) |
= 12 são -2, 1, 2 e 5. Justifique.
Questão 7
Uma indústria pode produzir, por dia, até 20 unidades de
um determinado produto. O custo C (em R$) de produção
de x unidades desse produto é dado por:
Questão 2
Dada a função: f(x) = | x - 1 | + 1, x Æ [-1, 2],
a) esboce o gráfico da função f;
b) calcule a área da região delimitada pelo gráfico da
função f, pelo eixo das abscissas e pelas retas x = -1 e x =
2.
6.3.4
Questão 3
O volume de água em um tanque varia com o tempo de
acordo com a seguinte equação:
V = 10 - |4 - 2t| - |2t - 6|, t Æ IRø
Nela, V é o volume medido em m¤ após t horas, contadas a
partir de 8h de uma manhã.
Determine os horários inicial e final dessa manhã em que o
volume permanece constante.
Questão 4
Sejam f e g as funções definidas para todo x Æ IR por f(x)
= x£ - 4x + 4 e g(x) = |x - 1|.
a) Calcule f(g(x)) e g(f(x)).
b) Esboce os gráficos das funções compostas fog e gof.
Questão 5
Considere a função f: R ë R definida por f(2x) = |1 - x |.
Determine os valores de x para os quais f(x) = 2.
a) Se, em um dia, foram produzidas 9 unidades e, no dia
seguinte, 15 unidades, calcule o custo de produção das 24
unidades.
b) Determine a produção que corresponde a um custo
máximo.
Questão 8
Sejam a e b dois números reais positivos tais a < b e a + b =
4. Se o gráfico da função y = |x - a| + |x - b| coincide com a
função y = 2 no intervalo a ´ x ´ b, calcule os valores de a
e b.
Questão 9
Uma piscina de borda retangular e paredes laterais verticais
está completamente vazia. Para enchê-la será usada uma
mangueira que despeja água a uma vazão constante. A
piscina ficará cheia até a borda 30 minutos após o início do
processo. A figura a seguir mostra uma seção transversal da
piscina por um plano vertical paralelo a um par de lados da
borda.
Questão 6
Sejam as funções f(x) = |x - 1| e g(x) = (x£ + 4x - 4).
a) Calcule as raízes de f(g(x)) = 0.
6.11.4
b) Esboce o gráfico de f(g(x)), indicando os pontos em que
o gráfico intercepta o eixo cartesiano.
1
São idênticas todas as seções transversais do interior da
piscina paralelas à seção mostrada na figura, onde também
estão assinalados os ângulos retos.
a) Determine o tempo necessário para que o nível h de água
na piscina atinja 1 metro de profundidade.
b) Se t representa o tempo contado a partir do momento em
que se começa a encher a piscina, 0 ´ t ´ 30, expresse t
como função da altura h da água na piscina.
Questão 10
Questão 13
O conjunto de soluções da equação | x - 1 | + | x - 2 | = 3 é:
a) {0,1}
b) {0,3}
c) {1,3}
d) {3}
e) { }
Questão 14
Durante o ano de 1997 uma empresa teve seu lucro diário L
dado pela função
L(x) = 50 ( | x - 100 | + | x - 200 | )
onde x = 1, 2, ..., 365 corresponde a cada dia do ano e L é
dado em reais.
Determine em que dias (x) do ano o lucro foi de
R$10.000,00.
Questão 11
A soma dos valores inteiros de x que satisfazem
simultaneamente as desigualdades: | x - 5 | < 3 e | x - 4 | µ 1
é:
a) 25
b) 13
c) 16
d) 18
e) 21
Se y = x - 2 + | x - 2| x | |, x Æ IR, então o menor valor que
y pode assumir é:
a) - 2.
b) - 1.
c) 0.
d) 1.
e) 2.
Questão 15
Se x é uma solução de |2x - 1| < 5 - x, então:
a) 5 < x < 7.
b) 2 < x < 7.
c) - 5 < x < 7.
d) - 4 < x < 7.
e) - 4 < x < 2.
Questão 12
O módulo | x | de um número real x é definido por | x | = x,
se x µ 0, e | x | = - x, se x < 0. Das alternativas a seguir, a
que melhor representa o gráfico da função f(x) = x . | x | 2x + 2 é:
6.3.4
2