1
02) Determine f(x) cujo gráfico está ilustrado abaixo.
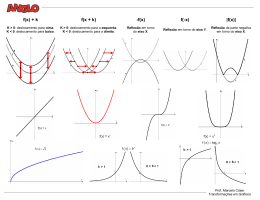
FUNÇÕES DE 1º GRAU
Uma função de 1º grau é caracterizada pela seguinte
lei:
Observações:
1) O fator a determina o crescimento da função: se
x  1 , então y  a . De fato, a 
y
.
x
Se a for positivo, a função é crescente; se for
negativo, a função é decrescente. Para a nulo, a função
é constante.
2) O fator b corresponde à ordenada do ponto o gráfico
de f(x) intercepta o eixo y.
03) (FGV) Uma fábrica de bolsas tem um custo fixo
mensal de R$ 5.000,00. Cada bolsa fabricada custa
R$ 25,00 e é vendida por R$ 45,00. Para que a fábrica
tenha um lucro mensal de R$ 4.000,00, ela deverá
fabricar x bolsas. O valor de x é:
EXERCÍCIOS DE AULA
01) Esboce o gráfico de f(x) = 2x - 2
a) 300
b) 350
c) 400
d) 450
e) 500
Prof. Marcelo Cóser
Intensivo 2009 - M3
2
04) (UFRJ) Uma operadora de celular oferece dois
planos no sistema pós-pago. No plano A, paga-se uma
assinatura de R$ 50,00 e cada minuto em ligações
locais custa R$ 0,25. No plano B, paga-se um valor fixo
de R$ 40,00 para até 50 minutos em ligações locais e,
a partir de 50 minutos, o custo de cada minuto em
ligações locais é de R$ 1,50. Determine a partir de
quantos minutos, em ligações locais, o plano B deixa
de ser mais vantajoso do que o plano A.
O gráfico de uma função de 2º grau sempre será
uma parábola, e, para esboçarmos seu gráfico, é
preciso analisar de dois a quatro fatores:
Concavidade da parábola
Depende
somente
do sinal
de a
Raízes
As raízes são os pontos onde o gráfico intercepta o
eixo das abscissas. Ou seja, tais que f(x) = 0. Assim, o
cálculo das raízes depende da resolução da equação
de 2º grau ax² + bx + c = 0, que, dependendo do sinal
de   b 2  4ac , pode ter duas raízes reais distintas,
uma raiz real dupla ou duas raízes complexas
conjugadas.
Não é difícil entender cada caso:
FUNÇÕES DE 2º GRAU
São duas as principais formas de expressar a lei de
uma função de 2º grau:
f(x) = ax² + bx + c, com a  0 .
f(x) = a.(x - R1).(x - R2), com R1 e R2 raízes de f(x).
É possível observar que as duas maneiras são
distintas, mas equivalentes. Ainda, o valor de a é o
mesmo para ambas. Cada uma delas apresenta
vantagens e desvantagens quando comparada com a
outra, como veremos a seguir.
Observe que quando
0
o gráfico de f(x)
permanece sempre acima ou abaixo do eixo das
abscissas, dependendo do sinal de a. Assim, f(x) será
sempre positiva ou sempre negativa se e somente
se  < 0 .
Prof. Marcelo Cóser
Intensivo 2009 - M3
3
Observações:
- A soma das raízes de uma equação de 2º grau
ax² + bx + c = 0 pode ser obtida a partir de
R1 + R 2 
b   b   2b
b


- .
2a
2a
2a
a
- De modo análogo, o produto das raízes será dado por
 b     b    c
R1  R 2  
  
  .
 2a   2a  a
EXERCÍCIOS DE AULA
05) Determine m de modo
que f(x) = x² - 6x + m não
possua raízes reais.
IMPORTANTE: as parábolas que representam o
gráfico de uma função são simétricas em relação à
reta vertical que passa pelo vértice.
A partir dessa simetria, é possível deduzir que a
abscissa do vértice (xV) de f(x) = ax² + bx + c será
xV =
-b
R1 + R 2
ou x V =
2a
2
A ordenada do vértice (yV) será y V = f  x v  .
EXERCÍCIOS DE AULA:
06) Determine m de modo
que f(x) = x² - 6x + m seja
positiva para qualquer
valor de x.
07) Determine a função de 2º grau cujo gráfico está
esboçado abaixo.
Ponto de intersecção com o eixo das ordenadas
O gráfico de f(x) intercepta o eixo y quando x = 0.
Ou seja, a ordenada desse ponto é dada por f(0). Se a
lei for dada na forma geral f(x) = ax² + bx + c, f(0) = c.
Vértice da parábola
O vértice da parábola é o ponto de máximo (a < 0) ou
ponto de mínimo (a > 0) da função.
Prof. Marcelo Cóser
Intensivo 2009 - M3
4
08) Esboce o gráfico de f(x) = x² - 6x + 8.
DOMÍNIO E IMAGEM DE UMA FUNÇÃO
Domínio de uma função f(x) é o conjunto de valores de
x para os quais a função está definida. Ou seja, são os
valores de x para os quais faz sentido aplicar a função.
Esse conjunto é definido na maioria das vezes a partir
de restrições, que podem ser de caráter teórico ou
prático.
Imagem de uma função f(x) é o conjunto de valores de
y gerados pela aplicação dos valores de x pertencentes
ao domínio da função. Graficamente, são as ordenadas
que estão associadas ao gráfico da função.
Restrições Teóricas
09) (PUCRS) Na figura, temos a representação
geométrica
de
uma
parábola
de
equação
São aquelas impostas pelas condições de existência de
determinadas operações matemáticas. As mais
comuns:
y  ax 2  bx  c . Para esta parábola, determine os
sinais dos produtos ab, ac e bc.
Restrições Práticas
São aquelas determinadas pelo contexto do problema.
Por exemplo, medidas geométricas (lado, área, volume,
etc.) devem ser positivas, o número de unidades pode
ser limitado pelo estoque, dentre outras possibilidades.
b < 0  f(x) é decrescente em x = 0
b > 0  f(x) é crescente em x = 0
É preciso muita atenção na leitura do enunciado.
b = 0  f(x) é máxima ou mínima em x = 0
Prof. Marcelo Cóser
Intensivo 2009 - M3
5
EXERCÍCIOS DE AULA
12) Resolva as inequações:
10) (UFRGS) Na figura abaixo, estão representados
três quadrados. A área do quadrado maior é 25, e a
soma das áreas dos quadrados hachurados é A(x). A
função A(x) é crescente no intervalo:
a) x 2  9
a)
b)
(0, 3/2)
(0, 5/2)
c)
(5 / 2,  )
d)
e)
(3/2, 5)
(5/2, 5)
11) (UFRGS) A partir de dois vértices opostos de um
retângulo de dimensões 7 e 5, marcam-se quatro
b) Determine o domínio de f  x  
1
2
.
 x  2x  2
pontos que distam x de cada um desses vértices.
Ligando-se esses pontos, como indicado na figura
abaixo, obtém-se um paralelogramo P. Considere a
função f, que a cada x pertencente ao intervalo (0, 5)
associa a área f(x) do paralelogramo P. O conjunto
imagem da função f é o intervalo:
a)
b)
c)
d)
(0, 10]
(0, 18)
(10, 18]
[0, 10]
e)
(0, 18]
A resolução gráfica de inequações é altamente recomendada!
Prof. Marcelo Cóser
Intensivo 2009 - M3
6
MÓDULO
EXERCÍCIOS
A definição de módulo diz que
a, se a  0
a 
.
 a, se a  0
Repare que -a, no caso, não indica um número
negativo, pois a já seria negativo. O sinal “-“, aqui,
indica somente uma troca de sinal.
Geometricamente, o módulo de a pode ser entendido
como a distância do ponto a à origem na reta real. De
acordo com essa perspectiva, é importante notar que a
equação |a| = 2, por exemplo, tem duas soluções. De
fato, se a = 2, a distância do ponto (2, 0) até a origem
vale 2. No entanto, o mesmo acontece para a = -2.
Assim, equações na
forma a  b, b  0,
possuem duas
soluções: a = b e a = -b
EXERCÍCIOS DE AULA
13) Esboce o gráfico de f  x   x e de g  x  
x
x
01) (PUCSP) Um grupo de amigos "criou" uma nova
unidade de medida para temperaturas: o grau Patota.
Estabeleceram, então, uma correspondência entre as
medidas de temperaturas em graus Celsius (°C), já
conhecida, e em graus Patota (°P), mostrada na tabela
abaixo. Lembrando que a água ferve a 100°C, então,
na unidade Patota ela ferverá a:
o
o
P
a)
96º
b)
88º
20
40
d)
64º
e)
56º
60
48
C
c)
78º
02) (UFRGS) Um grupo de estudantes dedicado à
confecção de produtos de artesanato gasta R$ 15,00
em material, por unidade produzida, e, além disso, tem
um gasto fixo de R$ 600,00. Cada unidade será
vendida por R$ 85,00. Quantas unidades terão de
vender para obterem um lucro de R$ 800,00?
a)
7
b)
10
c)
12
d)
15
e)
20
.
03) (UFRGS) Considere o gráfico abaixo, que
apresenta a taxa média de crescimento anual de certas
cidades em função do número de seus habitantes. A
partir desses dados, pode-se afirmar que a taxa média
de crescimento anual de uma cidade que possui
750.000 habitantes é:
a) 1,95%
b) 2,00%
c) 2,85%
d) 3,00%
e) 3,35%
14) Resolva a inequação x  2  x 2 .
04) (UFRGS) O ônibus X parte da cidade A com
velocidade constante de 80 km/h, à zero hora de certo
dia. Às 2 horas da madrugada, o ônibus Y parte da
mesma cidade, na direção e sentido do ônibus X, com
velocidade constante de 100 km/h. O ônibus Y vai
cruzar com o ônibus X, pela manhã, às:
a)
6h
b)
8h
c)
10 h
d)
11 h
e)
12 h
Prof. Marcelo Cóser
Intensivo 2009 - M3
7
05) (UFRGS) Em março de 2007, o menor preço
oferecido por uma companhia telefônica para ligação
do Brasil para os Estados Unidos era de R$ 0,95 o
minuto. O mesmo serviço pela internet custava R$ 0,05
o minuto e mais R$ 0,10 da taxa de conexão da
chamada. Em ambas as situações, o pereço por
segundo correspondia a
08) (UNIRIO) Considere a figura abaixo, onde um dos
lados do trapézio retângulo se encontra apoiado sobre
o gráfico de uma função f. Sabendo-se que a área da
região sombreada é 9 cm², a lei que define f é:
1
do preço por minuto.
60
Nessas condições, para que uma ligação telefônica, do
Brasil para os Estados Unidos, tivesse um custo menor
via companhia telefônica do que via internet, a duração
dessa ligação deveria ser, em número inteiro de
segundos, no máximo, de:
a)
6
b)
7
c)
8
d)
9
e)
a)
y
7x
2
6
b)
y
3x
1
4
c)
y
2x
1
5
d)
y
5x
1
2
e)
y
4x
1
3
10
06) (UERJ) Em uma partida, Vasco e Flamengo
levaram ao Maracanã 90.000 torcedores. Três portões
foram abertos às 12 horas e até as 15 horas entrou um
número constante de pessoas por minuto. A partir
desse horário, abriram-se mais 3 portões e o fluxo
constante de pessoas aumentou.Os pontos que
definem o número de pessoas dentro do estádio em
função do horário de entrada estão contidos no gráfico
abaixo. Quando o número de torcedores atingiu 45.000,
o relógio estava marcando 15 horas e:
a) 20 min
b) 30 min
c) 40 min
d) 50 min
07) (UFF) Um reservatório, contendo inicialmente 400
litros de água, começa a receber água a uma razão
constante de 3 litros por segundo, ao mesmo tempo em
que uma torneira deixa escoar água desse reservatório
a uma razão, também constante, de 1 litro por
segundo. Considerando o instante inicial (t = 0) como o
instante em que o reservatório começou a receber
água, determine uma expressão para o volume (V), em
litros, de água no reservatório em função do tempo
decorrido (t), em segundos, a partir do instante inicial.
09) (UNESP) Por uma mensagem dos Estados Unidos
para o Brasil, via fax, a Empresa de Correios e
Telégrafos (ECT) cobra R$ 1,37 pela primeira página e
R$ 0,67 por página que se segue, completa ou não.
Qual o número mínimo de páginas de uma dessas
mensagens para que seu preço ultrapasse o valor de
R$ 10?
a)
8
b)
10
c)
12
d)
14
e)
16
10) (UFPE) O preço da corrida de táxi na cidade R é
calculado adicionando um valor fixo de R$ 2,50 a
R$ 1,30 por cada quilômetro rodado, enquanto na
cidade S o preço é obtido adicionando um valor fixo de
R$ 3,40 a R$ 1,25 por quilômetro rodado. A partir de
quantos quilômetros rodados, o táxi da cidade R deixa
de ser mais barato que o da cidade S?
11) (UFPE) Em 01/11/2001 Júnior e Ricardo possuem
em suas contas correntes R$ 4.500 e R$ 3.200
respectivamente. Se, no primeiro dia de cada mês
subseqüente a novembro de 2001, Júnior saca R$ 50 e
Ricardo deposita R$ 50, quando o valor da conta
corrente de Ricardo ultrapassará o valor da conta de
Júnior, pela primeira vez?
a)
d)
OUT/2002
FEV/2003
b)
e)
NOV/2002
MAR/03
c)
JAN/2003
Prof. Marcelo Cóser
Intensivo 2009 - M3
8
12) (UNB) Cada bilhete vendido em um parque de
diversões dá direito à utilização de apenas um
brinquedo, uma única vez. Esse parque oferece aos
usuários três opções de pagamento:
I. R$ 2,00 por bilhete;
II. valor fixo de R$ 10,00 por dia, acrescido de R$ 0,40
por bilhete;
III. valor fixo de R$ 16,00 por dia, com acesso livre aos
brinquedos.
Com base nessa situação, julgue os itens a seguir.
(
(
(
)
Se uma criança dispõe de R$ 14,00, a opção
I é a que lhe permite utilizar o maior número
de brinquedos.
)
Se x representa o número de vezes que uma
pessoa utiliza os brinquedos do parque, a
função f que descreve a despesa diária
efetuada, em reais, ao se utilizar a opção III,
é dada por f(x)=16x.
É possível a um usuário utilizar determinado
número de brinquedos em um único dia, de
modo que a sua despesa total seja a mesma,
independente da opção de pagamento
)
escolhida.
13) (UFRGS) Considerando A = {x   /  1  x  10} , e
sendo R a relação em A formada pelos pares (x, y) tais
que y = 2x - 1, o domínio e a imagem dessa relação
correspondem, respectivamente, a:
a)
b)
c)
d)
e)
{0,
{1,
{0,
{1,
{1,
1,
2,
1,
2,
2,
2, 3} e {1, 3,
3, 4} e {3, 5,
2, 3, 4} e {0,
3, 4, 5} e {1,
3, 4, 5} e {0,
5, 7}
7, 9}
2, 4, 6, 8}
3, 5, 7, 9}
2, 4, 6, 8}
15) (UFES) Um fabricante de bonés opera a um custo
fixo de R$ 1.200 por mês (correspondente a aluguel,
seguro e prestações de máquinas). O custo variável
por boné é de R$ 2. Atualmente são comercializadas
1.000 unidades mensalmente, a um preço unitário de
R$ 5. Devido à concorrência no mercado, será
necessário haver uma redução de 30% no preço
unitário de venda. Para manter seu lucro mensal, de
quanto deverá ser o aumento na quantidade vendida?
16) (UFRGS) Na
figura ao lado, a
região sombreada do
plano xy é descrita
pelas desigualdades
da alternativa:
a) 0  x  4 e 0  y  5  x
b) 0  x  5 e 0  y  5  x
c) 1  x  4 e 0  y  5  x
d) 1  x  4 e 0  y  5
e) 1  x  4 e 0  y  5  x
17) (UFRGS) Se o gráfico tem a
expressão y = ax² + bx + c, os
valores de a, b e c são,
respectivamente,
a)
b)
c)
d)
e)
-3/2, -1 e 3
1, -3/2 e 3
1, -1 e 3/2
1, 8 e 3
4, 8 e 3
18) (UFRGS) A parábola na figura abaixo tem vértice
no ponto (-1, 3) e representa a função quadrática
f  x   ax 2  bx  c . Portanto, a + b é:
14) (UNICAMP) Três planos de telefonia celular são
apresentados na tabela abaixo. A partir de quantos
minutos de uso mensal o plano A é o mais vantajoso?
PLANO
CUSTO FIXO
MENSAL
CUSTO ADICIONAL
POR MINUTO
A
R$ 35
R$ 0,50
B
R$ 20
R$ 0,80
C
0
R$ 1,20
a)
b)
c)
d)
e)
-3
-2
-1
0
1
Prof. Marcelo Cóser
Intensivo 2009 - M3
9
19) (PUCPR) O gráfico de uma função do segundo
grau tem seu eixo de simetria na reta x = 3, tem uma
raiz igual a 1 e corta o eixo dos y em y = 25. Então, seu
conjunto imagem é:
a)
 20,   
d)
 , 20
b)
20,   
e)
 , 25
c)
 ,
 20 
20) (UDESC) Seja ABCD
um quadrado de área
unitária. São tomados
dois pontos P e Q, com
|AP| + |AQ| = |AD|.
Calcule o maior valor
para a área do triângulo
APQ.
b)
0
c)
1
d)
2
e)
4
25) (PUCCAMP) Seja R um retângulo que tem 24 cm
de perímetro. Unindo-se sucessivamente os pontos
médios dos lados de R obtém-se um losango. Qual
deve ser a medida do lado desse losango, em cm, para
que sua área seja máxima?
3
b)
3 2
c)
6
d)
6 2
a)
b)
c)
d)
e)
e)
9
45 e 45
30 e 90
36 e 72
40 e 60
20 e 120
27) (UFF) Um muro, com 6 metros de comprimento,
será aproveitado como parte de um dos lados do
cercado retangular que um criador precisa construir.
Para completar o contorno desse cercado, ele usará 34
metros de cerca. Determine as dimensões do cercado
retangular de área máxima que ele poderá construir.
d)
28) (UFMG) Observe a figura. Nessa figura, está
representada a parábola de vértice V, gráfico da função
de segundo grau cuja expressão é:
e)
22) (UFPE) Qual o maior valor assumido pela função
f : [7, 10]   definida por f(x) = x² - 5x + 9?
P2
18
b)
P2
9
c)
P2
6
d)
P2
4
a) y =
x2
- 2x
5
b) y = x² - 10x
c) y = x² + 10x
23) (UFRGS) Uma das dimensões de certo retângulo é
o dobro da outra. A expressão algébrica da área A,
desse retângulo, em função do seu perímetro P, é:
a)
-1
26) (UFRN) O Sr. José dispõe de 180 metros de tela
para fazer um cercado retangular, aproveitando, como
um dos lados, parte de um extenso muro reto.O
cercado compõe-se de uma parte paralela ao muro e
três outras perpendiculares a ele. Para cercar a maior
área possível, com a tela disponível, os valores de x e y
são, em metros, respectivamente:
b)
c)
a)
a)
21) (UFRGS) Considere
o gráfico de y = f(x) ao
lado. O gráfico de
g(x) = x.f(x) é:
a)
24) (PUCRS) Se x e y são números reais, com
x - y = 2, então o valor mínimo de z = x² + y² é:
e)
P2
2
d) y =
x2
- 10x
5
e) y =
x2
+ 10x
5
Prof. Marcelo Cóser
Intensivo 2009 - M3
10
29) (PUCRJ) O número de pontos de intersecção das
duas parábolas y = x² e y = 2x² - 1 é:
a)
0
b)
1
c)
2
d)
3
e)
4
30) (UFMG) A função f(x) do segundo grau tem raízes
-3 e 1. A ordenada do vértice do gráfico de f(x), é igual
a 8. A única afirmativa VERDADEIRA sobre f(x) é:
a) f(x) = -2(x - 1)(x + 3)
b) f(x) = -(x - 1)(x + 3)
c) f(x) = -2(x + 1)(x - 3)
d) f(x) = (x - 1)(x + 3)
e) f(x) = 2(x + 1)(x - 3)
31) (UFPA) O vértice da parábola y = ax² + bx + c é o
ponto (- 2, 3). Sabendo que 5 é a ordenada onde a
curva corta o eixo vertical, podemos afirmar que:
a) a > 1, b < 1 e c < 4
b) a > 2, b > 3 e c > 4
c) a < 1, b < 1 e c > 4
d) a < 1, b > 1 e c > 4
e) a < 1, b < 1 e c < 4
32) (UFPE) O gráfico da função y = ax² + bx + c é a
parábola da figura a seguir. Os valores de a, b e c são,
respectivamente:
a) 1, - 6 e 0
b) - 5, 30 e 0
c) - 1, 3 e 0
d) - 1, 6 e 0
e) - 2, 9 e 0
33) (UFPE) Na questão a seguir escreva nos
parênteses (V) se for verdadeiro ou (F) se for falso. Se
a é um número real positivo, então o gráfico de
y = a(x² + 2x), x real:
(
(
(
(
(
)
)
)
)
)
é uma parábola que passa pela origem (0,0).
é simétrico em relação à reta x = -1.
é uma parábola cujo vértice é o ponto (-1, a).
está contido na reunião do 1º, 2º e 3º quadrantes
não intercepta a reta y = -a.
35) (UFRGS) Um menino chutou uma bola. Esta atingiu
altura máxima de 12 metros e voltou ao solo 8
segundos após o chute. Sabendo que uma função
quadrática expressa a altura y da bola em função do
tempo t de percurso, esta função é:
a) y = - t² + 8t
b) y = 
3t 2
+ 3t
8
c) y = 
3t 2
+ 6t
4
d) y = 
t2
+ 2t
4
e) y = 
2t 2 16t

3
3
36) (PUCMG) Na parábola y = 2x² - (m - 3)x + 5, o
vértice tem abscissa 1. A ordenada do vértice é:
a)
3
b)
4
c)
5
d)
6
e)
7
37) (UFMG) O ponto de coordenadas (3,4) pertence à
parábola de equação y = ax² + bx + 4. A abscissa do
vértice dessa parábola é:
a)
1
2
b)
1
c)
3
2
d)
2
38) (PUCCAMP) Na figura a seguir tem-se um
quadrado inscrito em outro quadrado. Pode-se calcular
a área do quadrado interno, subtraindo-se da área do
quadrado externo as áreas dos 4 triângulos. Feito isso,
verifica-se que A é uma função da medida x. O valor
mínimo de A, em cm², é:
a) 16
b) 24
c) 28
d) 32
e) 48
34) (PUCCAMP) A soma e o produto das raízes de
uma função do 2º grau são, respectivamente, 6 e 5. Se
o valor mínimo dessa função é -4, então seu vértice é o
ponto:
a) (3, -4)
 11 
b)  , 4 
2

c) (0, -4)
d) (-4; 3)
e) (-4, 6)
Prof. Marcelo Cóser
Intensivo 2009 - M3
11
39) (UNESP) Um ônibus de 40 lugares transporta
diariamente turistas de um determinado hotel para um
passeio ecológico pela cidade. Se todos os lugares
estão ocupados, o preço de cada passagem é R$
20,00. Caso contrário, para cada lugar vago será
acrescida a importância de R$ 1,00 ao preço de cada
passagem. Assim, o faturamento da empresa de
ônibus, em cada viagem, é dado pela função f(x) = (40
- x).(20 + x), onde x indica o número de lugares vagos
(0  x  40). Determine quantos devem ser os lugares
vagos no ônibus, em cada viagem, para que a empresa
1  x2
é positiva se,
2  2x  x 2
e somente se, x pertence ao intervalo:
44) (UFRGS) A função f  x  
a)
(-1, 1)
b)
(-1, 1]
c)
[-1, 1]
d)
 ,
e)
 ,
 1  1,   
 1  1,   
obtenha faturamento máximo.
45) (FGV) A função f, de IR em IR, dada por
f(x) = ax² - 4x + a tem um valor máximo e admite duas
raízes reais e iguais. Nessas condições, f(-2) é igual a:
40) (CESGRANRIO) O diretor de uma orquestra
percebeu que, com o ingresso a R$ 9,00 em média 300
a)
pessoas assistem aos concertos e que, para cada
redução de R$ 1,00 no preço dos ingressos, o público
aumenta de 100 espectadores. Qual deve ser o preço
para que a receita seja máxima?
a) R$ 9
b) R$ 8
c) R$ 7
d) R$ 6
R$ 5
41) (UFMG) Observe a figura, que representa o gráfico
de y = ax² + bx + c. Assinale a única afirmativa FALSA
em relação a esse gráfico.
a) ac é negativo.
b) b² - 4ac é positivo.
c) b é positivo.
d) c é negativo.
4
b)
2
c)
0
d)
-0,5
e)
-2
46) (FGV) O lucro mensal de uma empresa é dado por
L = -x² + 30x - 5, onde x é a quantidade mensal
vendida. Entre que valores deve variar x para que o
lucro mensal seja no mínimo igual a 195?
47) (PUCMG) O gráfico da função f(x) = x² -2mx + m
está todo acima do eixo das abscissas. O número m é
tal que:
a) m < 0 ou m > 1
b) m > 0
c) -1 < m < 0
d) -1 < m < 1
e) 0 < m < 1
48) (UFRGS) A equação 2mx 2  mx 
1
 0 possui 2
2
raízes reais distintas. Então:
42)
(UFRGS)
O
gráfico
da
função
quadrática
f  x   x  px  1 intercepta o eixo das abscissas em
2
dois pontos distintos, se e somente se:
a)
d)
p < -2
p < 0 ou p > 2
b)
e)
p<0
c) -2 < p < 2
p < -2 ou p > 2
43) (UFRGS) O domínio da função real de variável real
a) m = 0
b) m > 0
d) m < 0 ou m > 4
c) m < 4
e) 0 < m < 4
49) (UNESP) O gráfico da função quadrática definida
por y = x² - mx + (m - 1), com m real, tem um único
ponto em comum com o eixo das abscissas. Então, o
valor de y que essa função associa a x = 2 é:
definida por f(x)  (1  x)(3  x) é o intervalo:
a)
a)
( ,  3]
b)
[-3, -1)
d)
[-3, 1]
e)
[1,  )
c)
-2
b)
-1
c)
0
d)
1
e)
2
(-3, 0)
Prof. Marcelo Cóser
Intensivo 2009 - M3
12
50) (PUCRS) A função real f
é definida por
f  x   g  x  . A representação gráfica de g está na
figura abaixo. O domínio da função f é:
a)
b)
c)
d)
e)
[-12; 4]
[0; 4]
(0; 4)
(-2; 2)
[-2; 2]
51) (UFRGS) Na figura ao
lado, a equação da reta é
y = x + 1, e, a da parábola,
y = x² - 2x - 3. A região
hachurada é, então, formada
pelos pontos (x, y) tais que:
2
a) 1  x  3 e x  2x  3  y  x  1
GABARITO
2
b) 1  x  4 e x  2x  3  y  x  1
c) 1  x  3 e  3  y  1
d) 1  x  3 e  4  y  1
2
e) 1  x  4 e x  1  y  x  2x  3
01
E
02
E
03
C
04
C
05
A
06
B
07
08
E
09
D
10
18
11
C
12
FFF
13
D
14
51
15
1.000
16
C
17
E
18
A
19
A
20
1
8
21
E
22
93
23
A
24
D
25
B
26
B
27
10m
28
A
29
C
30
A
31
D
32
D
33
V V F V F
34
A
35
C
36
A
37
C
38
D
39
10 lugares vagos
40
D
41
C
42
E
44
A
45
E
47
E
48
D
51
B
52
A
V(t) = 400 + 2t
52) (PUCRS) A representação que segue é da função f,
dada por f(x) = ax² + bx + c, a  0 . O valor de
b
2

 4ac   a  b  c  é:
a)
b)
c)
d)
e)
0
1
2
-2
-1
46
49
43
D
10  x  20
D
50
E
Prof. Marcelo Cóser
Intensivo 2009 - M3