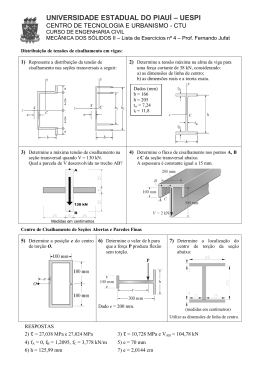
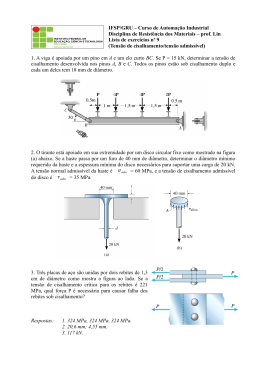
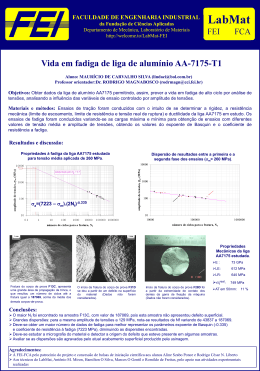
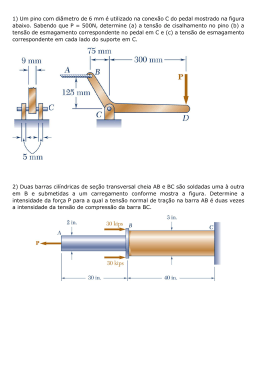
UNIVERSIDADE DE SÃO PAULO
Esco la de Eng enh a ria de Lo ren a – EEL
INTRODUÇÃO À MECÂNICA DOS SÓLIDOS – Prof. Carlos Baptista – 2a Lista de Exercícios
1. Um ponto na superfície de um sólido em equilíbrio está sob o estado de tensão indicado na figura. Determine as
tensões principais e os planos de corte principais, a máxima tensão de cisalhamento e o correspondente valor da
tensão normal. Represente graficamente o estado de tensão em um círculo de Mohr. Determine os planos em que
tensão normal é nula e calcule a tensão cisalhante nestes planos. (Resp.: Tensões principais = 255 MPa e -20 MPa,
atuam nos planos p1 = 63,43 e p2 = -26,57; tensão cisalhante máxima e correspondente tensão normal = 137,5
e 117,5 MPa; planos onde  = 0 são dados por  = -10,9 e  = -42,17; a tensão cisalhante vale 71,4 MPa)
2. Determinar o estado de tensão equivalente em um elemento orientado a 30 no sentido horário em relação ao
elemento mostrado na figura.
3. Para o estado de tensão indicado, as tensões principais são 30 e -100 MPa. Determine x e y, além dos ângulos de
corte principais e a máxima tensão de cisalhamento. (Resp.: x=-95MPa; y=25; max=65; p1=-11,3; p2=78,7)
4. Uma barra de cobre é mantida entre dois suportes rígidos, conforme a figura. Sua temperatura sofre um aumento de
38C. Determinar as tensões em todos os lados dos elementos A e B, mostrando os resultados em desenhos dos
elementos. Dados do material: E = 112 GPa e  = 5,6  10-6 C-1.
5. No elemento sob tensão plana, sabe-se que uma das tensões principais vale 26,1 MPa (tração). Determine a tensão
y. Determine a outra tensão principal e a orientação dos planos principais. Faça um esboço do elemento orientado
nas direções principais.
6. Nos cortes indicados sobre o ponto A, as tensões normais I e II têm módulo igual a 50 MPa (sendo que I é de
compressão) e III vale 100 MPa. Calcule a tensão de cisalhamento no corte II. (Resp.: II=-91,5MPa)
7. Para o elemento mostrado, determine o intervalo de valores de xy para os quais a tensão normal máxima é menor ou
igual a 60 MPa.
8. Um ponto de uma chapa fina está sujeito a dois estados de tensão sucessivos como mostrado. Determinar o estado
de tensão resultante em relação a um elemento orientado como do da figura da direita.