TESE DE
DOUTORADO
“ANÁLISES TEÓRICA E NUMÉRICA DO PROCESSO
DE PRENSAGEM EM CANAIS EQUIANGULARES”
ALUNO: NEIL DE MEDEIROS
ORIENTADORES: PROF. Dr. LUCIANO PESSANHA MOREIRA
PROF. Dr. JEFFERSON FABRÍCIO C. LINS
CO-ORIENTADOR: PROF. Dr. JAYME PEREIRA DE GOUVÊA
2008
Neil de Medeiros
“Análises Teórica e Numérica do Processo de Prensagem em
C a n a i s E q u i a n g u l a r e s .”
Estudo apresentado ao curso de pósgraduação em Engenharia metalúrgica da
Universidade Federal Fluminense, como
requisito para obtenção do título de doutor em
Engenharia Metalúrgica.
Orientadores: Prof. Dr. Luciano Pessanha Moreira
Prof. Dr. Jefferson Fabrício Cardoso Lins
Co-Orientador: Prof. Dr. Jayme Pereira de Gouvêa
Volta Redonda
2008
M488
Medeiros, Neil de
Análises teórica e numérica do processo de
prensagem em canais equiangulares / Neil de
Medeiros. – Volta Redonda, 2008.
217 f. : il., 30cm.
Tese (Doutorado em Engenharia Metalúrgica) –
Universidade Federal Fluminense, 2008.
1. Conformação mecânica. 2. Prensagem em canais
equiangulares. I. Título.
CDD 671.3
DEDICATÓRIA
Dedico esta tese às pessoas mais importantes para mim, minha querida mãe Maria
Lúcia Plínio de Medeiros principal responsável pela minha vida e a quem devo meu caráter
e disciplina ao trabalho e à adorada esposa Mabelle Biancardi Oliveira de Medeiros,
sempre paciente e generosa em meus momentos de desânimo e falta de estímulo. Ao
mesmo tempo, estendo esta dedicatória a meu pai Neil Ladeira de Medeiros, meu tio
Nathamar Ladeira de Medeiros e meu padrasto Antônio Miguel de Almeida.
Ofereço este trabalho em memória de entes queridos que me guiaram ao sucesso e
sempre confiaram em minha capacidade e que agora se encontram junto ao Pai, minha mãe
de criação Olga Maria da Conceição, meu avô Alcino Teixeira de Melo e meu padrinho
Celso Martins Ramos.
Esta dedicatória se estende também ao meu amigo, professor e orientador
Dr. Luciano Pessanha Moreira. A este devo a confiança em minha capacidade como
pesquisador além da paciência e tranqüilidade para me transmitir os ensinamentos da
complicada Mecânica dos Sólidos.
Aos demais orientadores deste trabalho Prof. Dr. Jefferson Fabrício Cardoso Lins e
Prof. Dr. Jayme Pereira de Gouvêa pelo estímulo ao desenvolvimento desta tese e
fundamentais ensinamentos que contribuíram de forma incomensurável ao longo dos anos
de pesquisa.
Ao Prof. Dr. Paulo Rangel Rios, pela oportunidade de experimentar a pesquisa ao
me conceder as bolsas de estudo em nível de mestrado (2003) e doutorado (2005) quando
ocupava o cargo de coordenador do Programa de Pós-graduação em Engenharia
Metalúrgica da Escola de Engenharia Industrial Metalúrgica de Volta Redonda –
EEIMVR / UFF.
AGRADECIMENTOS
O principal agradecimento dedico ao Pai, pela minha vida e pela paz nos momentos
em que me encontrei incapaz de prosseguir.
A meus pais, irmãs, demais familiares e amigos que sempre me incentivaram e
torceram pela minha vitória.
Ao meu sogro Hélio Gomes de Oliveira, à minha sogra Jorgete Ana Biancardi
Oliveira e ao meu cunhado Hélio José Biancardi Oliveira pelo apoio sincero.
Aos amigos Norman Duque Penedo, Gustavo Borges Amorim, Bruno Amaral
Pereira, Geovani Rodrigues e Márcia Regina Baldissera Rodrigues e aos demais colegas do
Programa de Pós-graduação em Engenharia Metalúrgica que me ajudaram no
desenvolvimento desta tese.
Ao estimado amigo João Gonçalves de Freitas pela estima e companheirismo.
À Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) pela
bolsa de estudos de Doutorado.
Aos demais professores do Programa de Pós-graduação em Engenharia
Metalúrgica, aos técnicos e demais profissionais da Escola de Engenharia Industrial
Metalúrgica de Volta Redonda – EEIMVR / UFF.
SUMÁRIO
1. INTRODUÇÃO GERAL
01
2. OBJETIVOS
04
2.1 OBJETIVO GERAL
04
2.2 OBJETIVOS ESPECÍFICOS
04
3. REVISÃO BIBLIOGRÁFICA
05
3.1 A ORIGEM DOS MÉTODOS DE DEFORMAÇÃO PLÁSTICA SEVERA
05
3.2 DEFORMAÇÃO POR TORÇÃO SOB ELEVADA PRESSÃO
06
3.3 FORJAMENTO MÚLTIPLO
07
3.4 PRENSAGEM EM CANAIS EQUIANGULARES
08
3.4.1 Definição e princípios da técnica PCEA
08
3.4.1.1 Rota A
09
3.4.1.2 Rota C
10
3.4.1.3 Rotas B
11
3.4.2 Estudos sobre o processamento de materiais via a técnica PCEA
13
3.4.2.1 Caracterização experimental
13
3.4.2.2 Modelos teóricos
22
3.4.2.3 Modelos numéricos
51
3.5 CONSIDERAÇÕES GERAIS ACERCA DA REVISÃO BIBLIOGRÁFICA
4. MATERIAIS E MÉTODOS
78
80
4.1 MATERIAIS
81
4.2 MÉTODOS
82
4.2.1 Experimento de prensagem a frio da liga Al 1100
82
4.2.2 Modelamento teórico
83
4.2.2.1 A formulação do método do limite superior
83
4.2.2.2 Soluções para o cálculo da carga de prensagem
86
4.2.2.3 Soluções para o cálculo das deformações plásticas efetivas
103
4.2.2.4 O método fatorial 2k para planejamento de experimentos
109
4.2.2.5 Análises teóricas realizadas no presente trabalho
113
4.2.3 Modelamento numérico via o método dos elementos finitos
115
4.2.3.1 Previsões numéricas e experimentais de carga para a liga Al 6070
116
4.2.3.2 Validação das soluções propostas para o cálculo da taxa de
deformação
120
4.2.3.3 Influência das condições de atrito
129
4.2.3.4 Comparação entre modelos bidimensionais e tridimensionais
132
5. RESULTADOS E DISCUSSÃO
5.1 EXPLORAÇÃO DOS MODELOS ANALÍTICOS PROPOSTOS
5.1.1 Validação dos modelos analíticos propostos
5.2 SIMULAÇÃO COMPUTACIONAL DA LIGA DE ALUMÍNIO Al 6070
135
136
142
143
5.2.1 Efeito da curva de encruamento
143
5.2.2 Efeitos geométricos da matriz
149
5.3 ANÁLISE FATORIAL 2k
153
5.3.1 Influência dos parâmetros considerados sobre a pressão e a deformação
efetiva
153
5.3.2 Superfícies de resposta
159
5.3.3 Perspectivas com base no planejamento fatorial 2k
165
5.4 ANÁLISES NUMÉRICAS DOS EFEITOS DE TAXA DE DEFORMAÇÃO
166
5.4.1 Análise das grandezas plásticas efetivas resultantes da tração uniaxial
166
5.4.2 Simulação da técnica PCEA
168
5.4.2.1 Previsões de carga de prensagem
168
5.4.2.2 Previsões de deformação plástica efetiva
174
5.4.2.3 Validação das soluções analíticas com efeito de taxa de deformação
183
5.5 INFLUÊNCIA DAS CONDIÇÕES DE ATRITO
187
5.5.1 Resistência ao cisalhamento relacionada às condições de atrito
187
5.5.2 Dependência entre a carga de prensagem e as condições de atrito
192
5.5.3 Distribuição das tensões e deformações plásticas efetivas
193
5.5.4 Mapeamento nodal da deformação plástica efetiva na zona uniforme
194
5.6 COMPARAÇÕES ENTRE MODELOS 2D e 3D
6. CONCLUSÕES
197
200
6.1 MODELAMENTO ANALÍTICO DA TÉCNICA PCEA
200
6.2 PLANEJAMENTO FATORIAL 2k
201
6.3 MODELAMENTO NUMÉRICO DA TÉCNICA PCEA
202
6.3.1 Modelos bidimensionais: prensagem da liga de alumínio Al 6070
202
6.3.2 Modelos bidimensionais: influência da viscoplasticidade na carga de
prensagem
203
6.3.3 Modelos bidimensionais: condições tribológicas críticas na técnica
PCEA
204
6.3.4 Comparação entre os modelos bidimensionais (2D) e
tridimensionais (3D)
205
7. SUGESTÕES PARA TRABALHOS FUTUROS
206
8. REFERÊNCIAS
208
9. ANEXOS
216
9.1 ANEXO 1: LISTA DE PUBLICAÇÕES
216
LISTA DE FIGURAS
Figura 1
Deformação por torção sob elevada pressão. Adaptado de Valiev et al. [3].
07
Figura 2
Princípio do forjamento múltiplo: (a) forjamento e usinagem ao
longo do primeiro eixo de deformação, (b) ao longo do segundo
eixo de deformação e (c) ao longo do terceiro eixo de deformação.
Adaptado de Valiev et al. [3].
08
Figura 3
Princípio da prensagem em canais equiangualares: o ângulo β
define o ângulo de abertura dos raios de adoçamento. Adaptado de
Furukawa et al. [14].
09
Figura 4
Desenho esquemático mostrando a metodologia de prensagem
referente à rota A.
09
Figura 5
Ni puro prensado por meio da rota A: (a) condição inicial;
(b) após um passe, (c) após dois passes e (d) após três passes.
Adaptado de Segal [6].
10
Figura 6
Desenho esquemático mostrando a metodologia de prensagem
referente à rota C.
11
Figura 7
Amostras de Ni puro prensadas pela rota C. (a) após dois passes e
(b) após três passes. Adaptado de Segal [6].
11
Figura 8
Esquema de processamento das rotas B. (a) rota BA e (b) rota BC.
12
Figura 9
Prensagem segundo as rotas A, B e C: (a) sistemas de deslizamento
em relação aos eixos X, Y e Z em passes consecutivos e
(b) distorções observadas em elementos cúbicos submetidos a oito
passes de prensagem. Adaptado de Valiev et al. [16].
13
Figura 10
Dependência entre tamanho de grão e propriedades mecânicas do
15
titânio puro com a temperatura de recozimento. Adaptado de Valiev [19].
Figura 11
Orientação entre o plano de alongamento dos grãos (1°passe) e o
plano cisalhante do segundo passe para as rotas BC ou BA.
Adaptado de Zhu et al. [25].
18
Figura 12
Figura 12: (a) evolução microestrutural observada durante a
prensagem de cobre puro e (b) curvas tensão-deformação após cada
passe. Adaptado de Dalla Torre et al. [30].
19
Figura 13
(a) esquema da técnica PCEA com destaque para o ângulo β e (b)
valores médios de dureza referentes ao Al puro e à liga Al 6061.
Adaptado de Xu et al. [32].
20
Figura 14
Variação do coeficiente de atrito com (a) carga de prensagem, para
a velocidade de 0,5 m/s e (b) velocidade para a carga de 20 N.
Adaptado de La et al. [34].
20
Figura 15
Dependência da tensão de escoamento do Al puro com
(a) temperatura de ensaio (b) taxa de deformação e (c) relação entre
s e n e a temperatura de prensagem. Adaptado de May et al. [35].
22
Figura 16
Classificação dos trabalhos teóricos reportados na literatura quanto
à escala de modelamento das previsões de pressão e deformação
oriundas da técnica PCEA.
23
Figura 17
Extrusão em canais equiangulares destacando a deformação do
elemento abcd em condições de cisalhamento simples.
Adaptado de Segal [6].
24
Figura 18
Comportamento do material durante a deformação via PCEA.
(a) Ψ = 0°; (b) 0º ≤ Ψ ≤ π - Φ e (c) Ψ = π - Φ. Adaptado de
Iwahashi et al. [37].
25
Figura 19
Análise da técnica PCEA pelo método do limite superior em
condições de deformação plana. Adaptado de Alkorta et al. [38].
26
Figura 20
(a) efeitos de β e Φ sobre p/σy; (b) sensibilidade de p/σy ao
expoente de encruamento e (c) dependência da deformação plástica
efetiva com a geometria da matriz. Adaptado de Alkorta et al. [38].
27
Figura 21
Matriz de prensagem composta por raios de adoçamento (R) iguais
e o respectivo hodógrafo de velocidades. Adaptado de Pérez [39].
28
Figura 22
(a) sensibilidade de (p/σy) às variações de R e Φ e (b) efeito das
condições de atrito sobre a pressão determinado via MEF. Pe e
Pe_frict se referem a m = 0 e 0,10 respectivamente.
Adaptado de Pérez [39].
29
Figura 23
Matriz composta por raios de adoçamento distintos. Adaptado de Pérez [40]. 30
Figura 24
Previsões de ε para geometrias distintas de matriz. Adaptado de Pérez [40]. 30
Figura 25
Geometria de deformação do modelo proposto por Altan et al. [41].
31
Figura 26
(a) relação entre o fator de atrito, raio interno e formação da zona
de deformação e (b) tamanho da zona de deformação em função do
fator de atrito. Adaptado de Altan et al. [41].
32
Figura 27
Curvas carga-deslocamento (a) real e (b) teórica. Adaptado de
Altan et al.[41].
33
Figura 28
Modelo de deformação da técnica PCEA proposto por Eivani et al. [43].
34
Figura 29
Relação entre pressão, atrito e geometria da matriz. (a) m = 0 e
(b) m = 0,5. Adaptado de Eivani et al. [43].
35
Figura 30
(a) relação entre deformação plástica efetiva e geometria da matriz
e (b) comparação entre as previsões teóricas e experimentais de
força de prensagem. Adaptado de Eivani et al. [43].
36
Figura 31
Geometria da matriz ilustrando o aparecimento da zona morta (III)
36
no modelo do método do limite superior proposto por Eivani et al. [44].
Figura 32
(a) relação entre força e atrito crítico; (b) efeitos de Φ e das
condições de atrito sobre ε e (c) comparação entre os resultados
teóricos e experimentais de força. Adaptado de Eivani et al. [44].
38
Figura 33
(a) matriz com Rint < Rext e (b) matriz com Rint > Rext. Adaptado de
Pérez et al. [45].
39
Figura 34
Comparação entre as previsões analítica e teórica de pressão
normalizada. Adaptado de Pérez et al. [45].
41
Figura 35
Figura 35: (a) dependência da pressão normalizada com Rext / L e H / L e
(b) relação entre a pressão normalizada, Rint / L e H / L. Adaptado de 42
Pérez et al. [45].
Figura 36
(a) dependência da pressão normalizada com Rext e Φ; (b) relação
entre p / σy, Rint e Φ e (c) relação entre p / σy, H e Φ. Adaptado de
Pérez et al. [45].
43
Figura 37
Geometria de deformação em ausência de atrito. Adaptado de
Segal [46].
44
Figura 38
Campos de linhas de deslizamento. (a) atrito idêntico sobre as
regiões de contato e (b) condições distintas de atrito. Adaptado de
Segal [46].
45
Figura 39
Histórico de deformação do elemento material abcd. Adaptado de
Segal [46].
46
Figura 40
(a) zona de deformação central e (b) zona de deformação bipartida.
Adaptado de Beyerlein et al. [47].
47
Figura 41
Descrição do campo de fluxo por linhas de fluxo. Adaptado de
50
Tóth et al. [48].
Figura 42
Classificação dos modelos numéricos aplicados ao estudo da técnica
PCEA.
51
Figura 43
Distorções da malha previstas pelo MEF (a) material encruável
(Al1100) e (b) material quase perfeitamente plástico (Al6061-T6).
Adaptado de Kim et al. [50].
53
Figura 44
Distribuição de deformações ao longo do tarugo. Adaptado de
Kim et al. [50].
53
Figura 45
(a) modelos para a análise de deformação plástica e (b) curvas de
carga versus deslocamento do punção obtidas durante a PCEA.
Adaptado de Kim [51].
54
Figura 46
Distribuição de deformações efetivas ao longo do tarugo.
(a) Φ = 90º; (b) Φ = 120º e (c) Φ = 135º. Adaptado de
Srinivasan et al. [52].
55
Figura 47
Carga de extrusão versus deslocamento do punção durante a técnica PCEA.
56
Adaptado de Kim [54].
Figura 48
Efeitos de parâmetros sobre a homogeneidade de deformações e a curvatura
da amostra: (a) ângulo Φ; (b) ângulo β; (c) parâmetros materiais e (d) atrito. 57
Adaptado de Dumoulin et al. [55].
Figura 49
(a) titânio puro deformado a 25ºC e (b) aço AISI 4340 deformado a 325ºC.
58
Adaptado de Semiatin et al. [56].
Figura 50
(a) contornos de deformação plástica efetiva e (b) temperatura final para a
prensagem não-isotérmica a quente de Ti-6Al-4V com taxa de deformação 59
de 2 s-1. Adaptado de Semiatin et al. [56].
Figura 51
(a) preenchimento do canal de saída da matriz em função de s, comparado
ao resultado experimental; (b) distribuição local de deformação para
diversos valores de s; (c) distribuição da taxa de deformação para diferentes 60
configurações de matriz e valores de s e (d) distribuição de danos em
função de Φ e s. Adaptado de Figueiredo et al. [57].
Figura 52
Ilustração esquemática da técnica PCEA. Adaptado de Kim [58].
Figura 53
Distribuição de valores da taxa de deformação (s-1). (a) malha grosseira e
63
(b) malha refinada. Adaptado de Kim [58].
Figura 54
Influência do ângulo β sobre a distribuição da taxa de deformação (s-1).
63
(a) β = 45º e (b) β = 90º. Adaptado de Kim [58].
Figura 55
Influência dos ângulos Φ e β sobre as previsões de taxa de deformação (s-1).
64
(a) β = 0º e (b) β = 45º. Adaptado de Kim [58].
61
Figura 56
Ilustração esquemática da técnica PCEA. Adaptado de Kim [58].
65
Figura 57
(a) algoritmo para o a simulação computacional utilizando o modelo de
encruamento baseado em densidade de discordâncias e (b) diagrama
68
esquemático ilustrando o procedimento de atualização para a simulação de
passes consecutivos de prensagem. Adaptado de Baik et al. [60].
Figura 58
(a) curvas de encruamento após cada um dos 4 passes, em comparação com
a condição inicial e (b) curva tensão-deformação efetiva para Al-puro e 69
valores experimentais obtidos após 1-4 passes. Adaptado de Baik et al. [60].
Figura 59
Células observadas por meio de microscopia eletrônica de transmissão após
69
(a) 1, (b) 2 e (c) 4 passes. Adaptado de Baik et al. [61].
Figura 60
Variações do tamanho médio da célula calculadas numericamente e
70
comparadas aos resultados experimentais. Adaptado de Baik et al. [60].
Figura 61
Distribuição de ε ao longo do eixo X. Adaptado de Suo et al. [63].
Figura 62
Modelos para a simulação continuada da prensagem em canais
72
equiangulares. Adaptado de Suo et al. [64].
Figura 63
Distribuição das deformações plásticas efetivas ao longo do plano X para
72
µ = 0. Adaptado de Suo et al. [64].
Figura 64
(a) esquemas de aplicação de contra pressão e (b) curvas de encruamento
obtidas para o Ti puro em diferentes temperaturas. Adaptado de 74
Son et al. [65].
Figura 65
Distribuição das deformações plásticas efetivas para os modelos de contra
pressão propostos. (a) forças de atrito; (b) contra pressão imposta sobre a
amostra e (c) deslocamento da parte inferior da matriz. Os resultados estão 75
ordenados para valores de contra pressão iguais a 100, 200 e 300 MPa. Em
todos os casos, m = 0,05 e β = 0°. Adaptado de Son et al. [65].
71
Figura 66
Distribuição das deformações plásticas efetivas para os modelos de contra
pressão propostos após 2, 3 e 4 passes. (a) forças de atrito, rota A; (b) forças
de atrito, rota C e (c) deslocamento da parte inferior da matriz com pressão 76
de 300 MPa, rota A. Em todos os casos, m = 0,05 e β = 0°. Adaptado de
Son et al. [65].
Figura 67
(a) deformações plásticas efetivas após 1, 2, 3 e 4 passes e (b) distribuição
de danos para 1 passe (esquerda) e dois passes (direita). Adaptado de 77
Jiang et al. [66].
Figura 68
Previsões de carga de prensagem. (a) após 1 passe; (b) após 2 passes.
Adaptado de Jiang et al. [66].
Figura 69
(a) aparato utilizado nos testes experimentais de prensagem da liga Al 1100
e (b) interior da matriz contendo um tarugo deformado ao longo do canal de 82
saída.
Figura 70
(a) linha de fluxo do ponto material q para matrizes com Rint < Rext e (b)
vista ampliada da região que compreende a linha de fluxo. Adaptado de
Pérez et al. [45].
87
Figura 71
(a) linha de fluxo do ponto material q para matrizes com Rint > Rext e (b)
vista ampliada da região que compreende a linha de fluxo. Adaptado de
Pérez et al. [45].
88
Figura 72
Relações para o volume diferencial do tarugo durante a prensagem.
(a) Rint < Rext e (b) Rint > Rext. Adaptado de Pérez et al. [45].
90
Figura 73
Determinação do ângulo β. (a) Rint < Rext e (b) Rint > Rext. Adaptado de
Pérez et al. [45].
91
Figura 74
Relação entre as coordenadas r e x do ponto material q. (a) Rint < Rext e
(b) Rint > Rext. Adaptado de Pérez et al. [45].
91
Figura 75
Parâmetros geométricos necessários à determinação de SD. (a) Rint < Rext e
(b) Rint > Rext. Adaptado de Pérez et al. [45].
92
Figura 76
Áreas de contato tarugo-matriz S1 e S2. Adaptado de Pérez et al. [45].
93
77
Figura 77
Curvas de escoamento determinadas a partir dos critérios de escoamento
102
de Tresca, Drucker e von Mises. (a) metais CCC e (b) metais CFC.
Figura 78
Geometrias de matriz para a determinação da deformação plástica
106
cisalhante. (a) Rint < Rext e (b) Rint > Rext. Adaptado de Luri et al. [89].
Figura 79
Modelos para a simulação da prensagem da liga Al6070. (a) sem
118
adoçamento e (b) com adoçamento externo.
Figura 80
Cubo discretizado por um único elemento SOLID 185 com destaque para
121
as áreas com condições de contorno.
Figura 81
Curvas de velocidade para as simulações para deformação do cubo em
tração uniaxial com sensibilidade à taxa de deformação. (a) V = 2 mm/s e 122
(b) V = 8mm/s.
Figura 82
Figura 82: Matrizes destinadas à validação da solução para a taxa de
deformação. (a) sem adoçamentos; (b) com adoçamento externo e 125
(c) raios de adoçamento iguais.
Figura 83
Curva velocidade vs tempo utilizada na simulação da prensagem em
126
canais equiangulares com efeito da taxa de deformação.
Figura 84
Nós utilizados no mapeamento das componentes de deformação ao longo
das direções horizontal e vertical. (a) matriz com adoçamento externo; (b)
128
matriz desprovida de adoçamentos e (c) matriz composta por raios de
adoçamento idênticos.
Figura 85
Matrizes com diferentes ângulos de interseção dos canais utilizadas nas
130
simulações. (a) Φ = 90º e (b) Φ = 120º.
Figura 86
(a) desenho esquemático dos lados do tarugo usados na determinação das
curvas de atrito e (b) nós utilizados no mapeamento dos deslocamentos, 131
pressão de contato e tensão cisalhante ao longo do tempo de simulação.
Figura 87
Esquemas para o mapeamento nodal da distribuição das deformações
plásticas efetivas ao longo da superfície deformada do tarugo. (a) Φ = 90º 132
e (b) Φ=120º.
Figura 88
Matrizes utilizadas na comparação entre modelos de simulação da técnica
PCEA. (a) bidimensional em condição de deformação plana e 133
(b) tridimensional.
Figura 89
Dependência entre p / σy e a geometria da matriz. (a) Φ e Rint e (b) Φ e Rext.
137
Relação entre σy e a geometria da matriz. (c) Φ e Rint e (d) Φ e Rext.
Figura 90
Dependência de p / σy com a geometria da matriz e as condições de atrito.
(a) Φ e m e (b) Rint / Rext e m.
Figura 91
Dependência de p / σy com os critérios de escoamento, geometria da
139
matriz e o atrito. (a) Φ e κ / σy; (b) Rint / Rext e κ / σy e (c) m e κ / σy.
Figura 92
Dependência entre as deformações plásticas efetivas e os parâmetros
141
geométricos da matriz. (a) ângulo Φ e Rint (b) ângulo Φ e Rext.
Figura 93
Validação dos modelos propostos para o cálculo da carga de prensagem.
142
Figura 94
Comparação entre as curvas de prensagem para a liga Al 6070.
(a) experimental [43] e (b) 2D numéricas relacionadas à máxima def.
plástica efetiva.
143
Figura 95
Condição de plasticidade referente à prensagem da liga Al 6070.
(a) ε = 1,16 e (b) ε = 0,26 .
145
Figura 96
Regiões de descolamento e perda de contato entre o tarugo e a matriz.
145
(a) após 5 mm deslocamento e (b) após 14 mm de deslocamento.
Figura 97
Curvas de deformação plástica efetiva. (a) ε = 1,16 e (b) ε = 0,26 .
Figura 98
Distribuição das grandezas plásticas efetivas. (a) e (c) deformação e tensão
148
para ε max = 1,16 ; (b) e (d) deformação e tensão para ε max = 0,26 .
138
147
Figura 99
Curvas de prensagem carga-deslocamento para a liga Al 6070.
149
(a) experimental [43] e (b) 2D numérica.
Estágios de deformação associados à prensagem através de matrizes com
adoçamento externo. (a) forjamento, após 7 mm; (b) forjamento e
Figura 100
150
compressão plana, após 10 mm e (c) forjamento e compressão plana,
após ~ 25 mm.
Figura 101
(a) condição de plasticidade referente à prensagem da liga Al 6070 e
151
(b) deformações plásticas efetivas em função dos deslocamentos impostos.
Figura 102 Efeitos de geometria da matriz. (a) previsões força e (b) previsões de ε .
152
Gráficos de probabilidade normal da influência dos parâmetros
Figura 103 considerados sobre as variáveis de interesse. (a) pressão e (b) deformação 156
plástica efetiva.
Figura 104
Influência de parâmetros geométricos da matriz sobre a pressão de
160
extrusão.
Figura 105 Efeitos combinados sobre a pressão. (a) Φ e m; (b) raios e m.
161
Figura 106
Efeitos combinados sobre a pressão. (a) velocidade de prensagem e
162
tribologia e (b) critério de plasticidade e tribologia.
Figura 107
Efeitos combinados sobre a pressão. (a) Φ e κ/σy ; (b) raios e κ/σy e
163
(c) velocidade inicial e κ/σy.
Figura 108 Efeitos combinados sobre a pressão. (a) Φ e V0 e (b) raios e V0.
164
Figura 109 Efeitos geométricos da matriz sobre a deformação plástica efetiva.
165
Figura 110 Efeito da velocidade de tração sobre o material modelo.
167
Previsões numéricas de força de prensagem para arranjos distintos de
Figura 111 matriz. (a) material modelo sem efeito de taxa e (b) material modelo com 168
efeito de taxa.
Estágios de deformação do tarugo em matrizes com adoçamentos iguais.
(a) regiões de forjamento e descolamento, após 4 mm; (b) descolamento e
Figura 112 contato com a base da matriz, após 8 mm; (c) contato com a parte superior 171
do canal de saída, após 16 mm e (d) preenchimento quase completo dos
canais pelo tarugo, após 25 mm.
Comparação entre as curvas de carga do material modelo com e sem o
Figura 113 efeito da taxa de deformação. (a) sem raios de adoçamento; (b) raio de 172
adoçamento externo e (c) raios de adoçamento iguais.
Comparação entre as curvas de tensão efetiva média do material modelo
Figura 114 com e sem o efeito da taxa de deformação. (a) sem raios de adoçamento; 173
(b) raio de adoçamento externo e (c) raios de adoçamento iguais.
Previsões de deformação plástica efetiva resultantes de geometrias
Figura 115 distintas para a matriz. (a) sem efeitos viscoplásticos e (b) com efeitos 174
viscoplásticos.
Iso-contornos de deformação plástica efetiva ao longo do tarugo
deformado para diferentes arranjos geométricos de matriz. (a) ausência de
Figura 116 adoçamentos-sem taxa; (b) ausência de adoçamentos com taxa; (c) 176
adoçamento externo-sem taxa; (d) adoçamento externo-com taxa; (e)
adoçamentos idênticos-sem taxa e (f) adoçamentos idênticos-com taxa.
Componentes de deformação plástica sobre a superfície do tarugo
deformado pela matriz sem adoçamentos. (a) direção vertical-sem taxa; (b)
Figura 117 direção vertical- com taxa; (c) direção horizontal-sem taxa; (d) direção 178
horizontal-com taxa; (e) previsões numéricas de ε -sem taxa e (f) previsões
numéricas de ε -sem taxa.
Componentes de deformação plástica sobre a superfície do tarugo
deformado pela matriz com raio de adoçamento externo. (a) direção
Figura 118 vertical-sem taxa; (b) direção vertical- com taxa; (c) direção horizontal- 180
sem taxa; (d) direção horizontal-com taxa; (e) previsões numéricas de ε sem taxa e (f) previsões numéricas de ε -sem taxa.
Componentes de deformação plástica sobre a superfície do tarugo
deformado pela matriz com raios de adoçamento iguais. (a) direção
Figura 119 vertical-sem taxa; (b) direção vertical- com taxa; (c) direção horizontal- 182
sem taxa; (d) direção horizontal-com taxa; (e) previsões numéricas de ε sem taxa e (f) previsões numéricas de ε -sem taxa.
Figura 120
Comparação entre previsões teóricas e numéricas de força. (a) sem raios de
184
adoçamento; (b) raio de adoçamento externo.
Figura 121
Comparação entre previsões teóricas e numéricas de força oriundas da
185
matriz com raios de adoçamento idênticos.
Figura 122
Figura 122: Previsões teóricas e numéricas de deformação plástica efetiva.
186
(a) sem adoçamentos; (b) adoçamento externo e (c) adoçamentos iguais.
Tensão cisalhante e pressão de contato obtidas junto aos nós localizados
Figura 123 sobre os lados esquerdo e direito do tarugo. (a) µ = 0,05; (b) µ = 0,10 e 188
(c) µ = 0,20.
Resultados nodais de deslocamento, pressão de contato e tensão cisalhante
Figura 124 em função do tempo de análise para Φ = 90º e µ = 0,20. (a) lado esquerdo 190
do tarugo; (b) lado direito do tarugo e (c) base do tarugo.
Figura 125
Tensões cisalhantes e pressões de contato obtidas para Φ = 120º ao longo
191
dos lados esquerdo e direito do tarugo. (a) µ = 0,05 e (b) µ = 0,10.
Figura 126
Dependência entre a carga e as condições de atrito. (a) Φ=90º e
192
(b) Φ=120º.
(a) distribuição de ε para Φ=90º; (b) distribuição de tensões
Figura 127 efetivas,Φ=90º; (c) distribuição de ε para Φ=120º e (d) distribuição de 193
tensões efetivas para Φ=120º.
Figura 128
Previsões nodais de ε ao longo da zona plástica uniforme para distintas
195
condições de atrito e Φ = 90º. (a) µ = 0,05; (b) µ = 0,10 e (c) µ = 0,20.
Figura 129
Previsões nodais de ε ao longo da zona plástica uniforme para diferentes
196
condições de atrito e Φ = 120º. (a) µ = 0,05; (b) µ = 0,10 e (c) µ = 0,20.
Figura 130
(a) curvas numéricas e experimental de carga e (b) valores numéricos e
198
experimental máximos de força.
Distribuição das grandezas plásticas efetivas ao longo da superfície da
Figura 131 peça. (a) 2D tensão; (b) 2D deformação; (c) 3D tensão e 199
(d) 3D deformação.
LISTA DE TABELAS
Tabela 1
Efeitos do número de passes e rotas (A e C) sobre a resistência à tração
(RT) e alongamento de aço baixo carbono. Adaptado de Shin et al. [22].
16
Tabela 2
Parâmetros utilizados. Adaptado de Dumoulin et al. [55].
57
Tabela 3
Propriedades mecânicas referentes aos materiais utilizados no presente
trabalho.
81
Tabela 4
Composição química da liga de alumínio Al 1100 (% em peso).
81
Tabela 5
Combinações entre as variáveis consideradas no método fatorial 26.
110
Tabela 6
Matriz de planejamento para o método fatorial 26.
111
Tabela 7
Parâmetros utilizados na exploração dos modelos analíticos propostos.
114
Tabela 8
Parâmetros utilizados no método fatorial 26.
115
Tabela 9
Valores de tempos e deslocamentos em função do modelo de matriz.
126
Tabela 10
Pressão de prensagem e deformação efetiva oriundas do método fatorial 26. 154
Tabela 11
Classificação dos efeitos quanto à probabilidade (Pj) de relevância sobre as
155
previsões de pressão e deformações plásticas efetivas.
Tabela 12
Análise de variância do tipo 26 realizada sobre os modelos propostos.
158
LISTA DE ABREVIATURAS, SIGLAS E SÍMBOLOS
A, BA, BC, C
Rotas de prensagem do tarugo segundo a
técnica PCEA.
b
Vetor de Burgers.
c
Parâmetro associado ao critério de
Drucker que permite o achatamento da
superfície de escoamento entre estados de
tração/compressão planas e cisalhamento.
CN
Parâmetro de falha por fatura do material
prensado, segundo Figueiredo et al. [57].
d
Tamanho de grão.
[nm]
dI
Deslocamento associado a ti
[mm]
dII
Deslocamento associado a tf
[mm]
D
Diâmetro das amostras utilizadas no
forjamento múltiplo.
[mm]
E
Módulo de elasticidade.
[GPa]
Er
Erro associado à escolha dos parâmetros
de relevância sobre a pressão ou a
deformação plástica efetiva.
Er
Erro médio relacionado aos parâmetros de
relevância.
f
Fração volumétrica das paredes celulares,
segundo Baik et al. [60].
f (σij , ε )
Função de escoamento plástico.
fo
Fração volumétrica inicial das paredes
celulares, segundo Baik et al. [60].
f∞
Saturação de f, segundo Baik et al. [60].
F (σij ) Mises
Função de geometria da curva
escoamento do critério de von Mises.
de
Fi
Forças externas aplicadas sobre a peça em
deformação plástica.
Fo
Variância.
G
Módulo de cisalhamento.
GL
Graus de liberdade associados a cada um
dos efeitos.
h
Altura das amostras
forjamento múltiplo.
H
Altura total do tarugo.
Hµ
Microdureza.
J1
Primeiro invariante do tensor Sij.
[MPa]
J2
Segundo invariante do tensor Sij.
[MPa]
J3
Terceiro invariante do tensor Sij.
[MPa]
K
Resistência mecânica ao escoamento
plástico do material deformado.
[MPa]
li
Comprimento instantâneo do tarugo sobre a
superfície de entrada da zona de deformação.
[mm]
lo
Comprimento instantâneo do tarugo sobre a
superfície de saída da zona de deformação.
[mm]
L
Largura dos canais da matriz.
[mm]
m
Fator de atrito estático.
mcrit
Fator de atrito crítico para a formação da
zona morta, segundo Eivani et al. [44].
mmax
Valor máximo do fator de atrito m para o
cálculo de xE.
mmin
Valor mínimo do fator de atrito m para o
cálculo de xE.
n
num
[kN]
[MPa]
utilizadas
no
Expoente de encruamento.
Número de réplicas realizadas sobre os
experimentos.
[mm]
[mm]
N
Número de passes de prensagem.
p
Pressão exercida pela punção sobre o
tarugo durante a extrusão.
p’
Parâmetro adimensional de pressão
considerado por Eivani et al. [43].
P
Força exercida pelo punção sobre o
tarugo.
r
Componente radial do
coordenadas cilíndricas
R
Raios de adoçamento.
[mm]
Rext
Raio de adoçamento externo.
[mm]
R ext max
Valor máximo do raio de adoçamento
externo para o cálculo de xA.
[mm]
R ext min
Valor mínimo do raio de adoçamento
externo para o cálculo de xA.
[mm]
Rint
Raio de adoçamento interno.
[mm]
R int max
Valor máximo do raio de adoçamento
interno para o cálculo de xB.
[mm]
R int min
Valor mínimo do raio de adoçamento
interno para o cálculo de xB.
[mm]
R1 e R2
Raios de adoçamento utilizados para a
definição de γ
[mm]
s
Expoente de sensibilidade à taxa de
deformação.
S
Superfície total do sólido sob deformação.
[mm2]
SD
Área de contato entre o tarugo e a matriz.
[mm2]
S∗D
Superfície
de
velocidades.
de
[mm2]
SF
Superfície com condições prescritas de
tração.
[mm2]
sistema
descontinuidade
[MPa]
[kN]
de
Sij
Tensor de componentes desviadoras do
tensor de tensão σij .
SQ
Soma dos quadrados dos
associados ao método fatorial 2k.
SQq
Soma individual dos quadrados de cada
efeito.
SQT
Soma total dos quadrados dos efeitos.
Sv
Superfície com condições prescritas de
velocidade.
[mm2]
S1
Área de contato entre o tarugo e as
paredes laterais da matriz.
[mm2]
S2
Área de contato entre o tarugo e as
paredes frontais da matriz.
[mm2]
ti
Tempo inicial de simulação.
[s]
tf
Tempo final de simulação.
[s]
t Γi
Tempo de residência do tarugo na
superfície de entrada da zona de
deformação.
[s]
t Γo
Tempo de residência do tarugo na
superfície de saída da zona de
deformação.
[s]
tT
Tempo total de prensagem gasto para a
mudança entre as componentes de
velocidade inicial e descontínuas.
[s]
t ZD
Tempo de residência do tarugo no interior
da zona de deformação.
[s]
T
Temperatura de prensagem.
[ºC/K]
vj
Campo virtual de velocidades.
[mm/s]
v∗i
Campo
virtual
descontínuas.
das
[MPa]
efeitos
velocidades
[mm/s]
V
Velocidade de prensagem definida por
Segal [45] e Beyerlein et al. [47].
[mm/s]
V*
Velocidade de descontinuidade.
[mm/s]
V0
Velocidade inicial de prensagem.
[mm/s]
V0 max
Valor máximo da velocidade inicial de
prensagem V0 para o cálculo de xF.
[mm/s]
V0 min
Valor mínimo da velocidade inicial de
prensagem V0 para o cálculo de xF.
[mm/s]
w
Espessura do tarugo
x
Componente que define a direção
horizontal no sistema de coordenadas
cartesianas
xA, ..., xABCDEF
Efeitos principais e suas combinações
referentes ao método fatorial 26.
y ijl2
Quadrado de cada respostas, em termos de
pressão ou deformação plástica efetiva.
α
Ângulo análogo a δ e η, de acordo com
Beyerlein et al. [47].
[Graus/Radianos]
β
Ângulo de abertura dos raios de
adoçamento dispostos na interseção dos
canais da matriz.
[Graus/Radianos]
χ
Função de fluxo do material durante a
prensagem, definida por Tóth et al. [48].
δ
Ângulo entre a direção horizontal e a
superfície de entrada da zona de
deformação.
δ ij
Operador linear delta de Kronecker.
∆εi
Incremento de deformação plástica
induzida ao material a cada passe.
[mm]
[Graus/Radianos]
∆t
∆v ∗
Tempo médio de deformação deduzido
por Kim [58].
[s]
Parcela da velocidade tangencial de
descontinuidades no campo v∗i .
[mm/s]
ε
Deformação plástica efetiva.
•
Taxa de deformação plástica efetiva.
ε
εa
εb
ε ij
•e
ε ij
•p
ε ij
Deformação plástica verdadeira associada
ao limite inferior de integração para
obtenção da tensão média de escoamento.
Deformação plástica verdadeira associada
ao limite superior de integração para
obtenção da tensão média de escoamento.
Tensor de deformações de Cauchy num
ponto.
Tensor taxa de deformação infinitesimal
elástica.
Tensor taxa de deformação infinitesimal
plástica.
ε ij
Tensor taxa de deformações infinitesimais
de Cauchy.
ε∗ij
Campo de taxa de deformação derivável
de v∗i .
εN
Deformação plástica efetiva atribuída ao
material após N passes de prensagem.
εp
Parcela plástica de deformação verdadeira.
•
•
Componente cisalhante principal do tensor
•
ε rθ
ε ij .
ε0
Encruamento inicial do material associado
aos testes de tração/compressão uniaxiais.
ε ZD
Deformação plástica efetiva atribuída ao
material na zona de deformação.
ε Γi
Deformação plástica efetiva atribuída ao
material na superfície de entrada da zona
de deformação.
ε Γo
Deformação plástica efetiva atribuída ao
material na superfície de saída da zona de
deformação.
φ
Semi-ângulo de interseção dos canais,
segundo Segal [45].
[Graus/Radianos]
Φ
Ângulo de interseção dos canais da matriz
utilizada na técnica PCEA.
[Graus/Radianos]
Φ max
Valor máximo do ângulo Φ para o cálculo
de xC.
[Radianos]
Φ min
Valor mínimo do ângulo Φ para o cálculo
de xC.
[Radianos]
ϕ
Ângulo entre Rext e o segmento O' q
[Radianos]
γ
Deformação plástica cisalhante imposta ao
tarugo por passe de prensagem.
γ Γi
Deformação plástica cisalhante imposta ao
material na superfície de entrada da zona
de deformação.
γ Γo
Deformação plástica cisalhante imposta ao
material na superfície de saída da zona de
deformação.
γi
Deformação plástica cisalhante induzida
ao material na superfície de entrada da
zona de deformação.
γo
Deformação plástica cisalhante induzida
ao material na superfície de saída da zona
de deformação.
•
γo
•r
γc
Taxa de deformação cisalhante
referência segundo Baik et al. [60].
de
Taxa de deformação cisalhante no interior
de cada célula, segundo Baik et al. [60].
•r
γw
Taxa de deformação cisalhante ao longo
das paredes de cada célula, segundo Baik
et al. [60].
Γi
Deformação plástica cisalhante imposta ao
material na zona de deformação.
Superfície de entrada da zona de
deformação.
Γo
Superfície de
deformação.
Γm
Superfície de zona morta de material.
η
Ângulo análogo
Segal [45].
ι
Parâmetro de viscosidade do material,
segundo a lei dinâmica de Peirce.
κ
Tensão de escoamento em condições de
cisalhamento puro.
κ / σy
Razão entre limites de escoamento.
( κ / σ y ) max
Valor máximo da razão κ/σy para o
cálculo de xD.
( κ / σ y ) min
Valor mínimo da razão κ/σy para o cálculo
de xD.
γ ZD
saída
a
da
δ,
zona
definido
de
por
λ
Multiplicador plástico ou módulo de
plasticidade.
µ
Coeficiente de atrito estático.
ν
Razão de Poisson.
ρc
Densidade de discordâncias observada no
interior de cada célula de material
considerada por Baik et al. [60].
ρm
Ângulo médio de abertura da zona de
deformação, segundo Beyerlein et al. [47].
ρt
Densidade total de discordâncias, segundo
Baik et al. [60].
•
[Graus/Radianos]
[MPa]
[Graus/Radianos]
ρw
Densidade de discordâncias observada ao
longo das paredes de cada célula de
material considerada por Baik et al. [60].
σ
Tensor de componentes principais do
tensor σij .
[MPa]
σm
Tensão média de escoamento em
condições de tração/compressão uniaxiais.
[MPa]
σij
Tensor de tensões de Cauchy num ponto.
[MPa]
∗
ij
Campo de tensões associado às condições
prescritas de tração e velocidade sobre as
superfícies SF e Sv.
[MPa]
σy
Tensão de escoamento em condições de
tração/compressão uniaxiais.
[MPa]
σu
Máxima resistência à tração.
[MPa]
τ
Componente cisalhante do tensor de
tensão σij.
[MPa]
τ cr
Tensão cisalhante no interior de cada
célula, segundo Baik et al. [60].
[MPa]
τ rw
Tensão cisalhante ao longo das paredes de
cada célula, segundo Baik et al. [60].
[MPa]
ξ
Origem do sistema de coordenadas (O)
segundo Altan et al. [41].
ξA, ..., ξABCDEF
Coeficientes parciais de regressão
associados ao método fatorial 26.
ξ0
Intercepto dos planos de cada superfície
de resposta.
Π
Função que define a superfície de
resposta.
Ψ
Ângulo de curvatura do material
processado em matrizes sem adoçamentos.
σ
[Graus/Radianos]
RESUMO
A técnica de prensagem em canais equiangulares consiste de um processo de
deformação plástica severa, no qual um tarugo é forçado a escoar sob condições de
cisalhamento simples através de uma matriz composta por canais idênticos interceptados a
um ângulo Φ. A literatura mostra diversos estudos acerca desta técnica. Todavia, estes se
limitam à exploração de resultados oriundos de alguns conjuntos específicos de
parâmetros. Neste contexto, o presente trabalho se destina a uma extensão, ao caso de
materiais que exibem encruamento e dependência com a taxa de deformação, das soluções
analíticas propostas por Pérez et al. [45] para os cálculos de carga e deformações plásticas
efetivas associadas a um único passe de prensagem a frio. Ao mesmo tempo, o método dos
elementos finitos foi aplicado ao desenvolvimento de modelos bidimensionais (2D) e
tridimensionais (3D) capazes de fornecer previsões acuradas de carga e deformações
efetivas oriundas de um único passe de prensagem a frio para materiais dependentes ou não
da taxa de deformação. Utilizando-se as ligas de alumínio Al 6070 e Al 1100, foi possível
explorar e atestar a validade das soluções propostas pela comparação a resultados
experimentais de carga. Além disso, a partir de modelos numéricos 2D, a avaliação da
condição de plasticidade permitiu verificar que o material se deformou plasticamente
apenas ao atravessar a região de interseção dos canais, fato este não explorado na literatura.
Ao mesmo tempo evidenciou-se a limitação de curvas de encruamento obtidas em
tração/compressão uniaxiais para a representação deste processo severo de conformação.
Em seguida, a análise qualitativa via o método fatorial 2k aplicado sobre os modelos
teóricos propostos possibilitou uma classificação satisfatória, por ordem de relevância, de
todos os parâmetros considerados. Ainda, essa análise indicou as configurações de matriz e
condições de prensagem que foram avaliadas com maior aprofundamento. A simulação
destes casos, considerando um material modelo com comportamento plástico distinto ora
independente ora sensível a efeitos viscoplásticos, revelou que o efeito de taxa de
deformação aumenta as previsões de carga, o que foi confirmado pelas curvas de tensão
efetiva de von Mises. Além disso, o cisalhamento prevaleceu como modo principal de
deformação nos casos de ausência de adoçamentos e presença do adoçamento externo. Em
matrizes com raios de adoçamento idênticos, o material foi deformado por cisalhamento e
dobramento. Por outro lado, utilizando-se um aço livre de intersticiais, verificou-se a
existência de um nível crítico de atrito que evita o fenômeno de aderência e a distribuição
heterogênea das deformações plásticas efetivas. Por fim, a consistência dos modelos
numéricos 2D e 3D foi investigada, em termos de carga, pela comparação aos resultados
experimentais oriundos da liga Al 1100.
Palavras-chave: Prensagem em canais equiangulares, método do limite superior, método
dos elementos finitos, análise fatorial 2k, carga de prensagem, deformação plástica efetiva.
ABSTRACT
The ECAP technique is a severe plastic deformation process in which a billet is
forced to flow under a simple shear condition through a die composed of identical channels
that are intercepted at an angle Φ. The literature presents a great number of studies related
to this technique. However, they are restricted to the exploration of results from specific set
of parameters. In this context, the present work is destined to include work-hardening and
strain-rate dependent materials in the upper-bound solutions proposed by Pérez and Luri to
estimate the pressing force/pressure and the effective plastic strains. These solutions are
associated to single pass of pressing at room temperature. At the same time, the finite
element method was applied for the development of two-dimensional (2D) and threedimensional (3D) models that are able to provide accurate predictions of pressing force and
effective plastic strains for either materials sensible or not to strain rate effects. Also, the
numerical models proposed are related to single pressing at cold. Using the aluminium
Al 6070 and Al 1100 alloys, the exploration and validation of the extended models was
performed by comparison with experimental results of force. Besides, from the analysis of
the 2D models, the evaluation of the plasticity condition allowed to verify that the material
was plastically deformed when it crosses the channels intersection region. This fact was
not explored in the recent literature. In addition, the limitation of the uniaxial tensile or
compression hardening curves for the representation of this severe forming process is
shown. Afterwards, the factorial 2k qualitative analysis permitted an appreciable
classification in order of relevance was showed for all considered parameters in the
proposed theoretical models. Moreover, this analysis indicated the die configurations and
pressing conditions that should be intensively investigated. The simulation of these cases,
considering a hypothetical material with plastic or viscoplastic behaviors, revealed that the
strain-rate effect increases the load predictions. This fact was confirmed by the curves of
von Mises effective stresses. In addition, shearing is the predominating deformation mode
in the absence of fillet radii and only with the outer fillet radii. For dies with identical fillet
radii, the material was deformed by shearing and bending. On the other hand, using
interstitial free steel, the existence of critical friction condition that avoids the adherence
phenomenon and the heterogeneous effective plastic strain distributions were verified.
Finally, the consistency of the 2D and 3D numerical models in the simulation of the equal
channel angular pressing was investigated in terms of load, by the comparison with the
experimental predictions for aluminum Al 1100 alloy.
Keywords: Equal channel angular pressing, upper bound method, finite element method,
factorial 2k analysis, pressing force, effective plastic strain.
1
1. INTRODUÇÃO GERAL
O processamento de materiais por meio de métodos de deformação plástica
severa (DPS) tem atraído grande interesse científico em razão das melhorias observadas
em suas propriedades mecânicas a partir do alto grau de refinamento microestrutural
induzido durante a o processo de conformação. Esta crescente atenção não se deve somente
às propriedades destes materiais, mas também às inúmeras vantagens dos materiais
processados via DPS em comparação a outros materiais deformados por meio de técnicas
tradicionais.
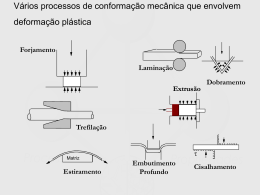
A imposição de deformações plásticas elevadas pelos tradicionais processos de
conformação mecânica (laminação a frio, extrusão, forjamento, entre outros) resulta em um
refinamento microestrutural. Entretanto, as microestruturas formadas a partir dos métodos
DPS são estruturas compostas de subestruturas com contornos de alto ângulo. De acordo
com Valiev [1] e Valiev et al. [2], a formação destas microestruturas está relacionada a
níveis elevados de deformações em temperaturas relativamente baixas e pressões elevadas.
Técnicas especiais de deformação mecânica foram desenvolvidas para a realização deste
princípio, destacando-se a prensagem em canais equiangulares (PCEA) que possibilita
obter materiais ultrafinos a partir de diferentes metais e ligas, segundo Valiev et al. [3].
A técnica PCEA, inventada por Segal [4-5] na década de 1970, fundamenta-se na
utilização do cisalhamento simples como uma operação de conformação. Ao mesmo
tempo, representa uma alternativa para a obtenção de materiais com propriedades
mecânicas superiores sem que haja múltiplas reduções em sua seção transversal inicial.
Nesta técnica, um tarugo maciço bem lubrificado é forçado a escoar através de uma matriz
com dois canais de seções transversais idênticas, interceptados geralmente a 90º. Sob estas
condições, o tarugo será deformado, principalmente, por cisalhamento simples ao
atravessar a zona de deformações que se localiza junto à interseção dos canais, como
mostram os trabalhos conduzidos por Segal [6-7].
2
A literatura aponta inúmeros estudos acerca deste método, que podem ser
classificados como experimentais [7-35], teóricos baseados principalmente no método do
limite superior [36-48, 80] e numéricos que envolvem notavelmente o método dos
elementos finitos [49-67, 78-79, 81-84], para análises e simulações do processamento de
diversos materiais. Em geral, os estudos experimentais são limitados a certas configurações
de geometria da matriz e algumas investigações acerca dos efeitos promovidos pelas
condições de ensaio como atrito e taxa de deformação, em razão dos custos envolvidos na
usinagem das ferramentas e preparações de amostras. Os estudos teóricos, por sua vez,
apresentam soluções analíticas para os cálculos de carga e deformações plásticas efetivas,
mas que se restringem à definição do escoamento pelo critério de von Mises. Ademais, as
pesquisas associadas à simulação computacional buscaram investigar a influência causada
por conjuntos específicos de parâmetros sobre as previsões de carga e a distribuição das
deformações ao longo da peça deformada. Assim, independentemente da abordagem
considerada, os trabalhos encontrados na literatura não permitem ainda classificar os
diversos parâmetros inerentes ao método PCEA quanto à relevância sobre as previsões de
carga e deformações. As limitações apresentadas na literatura acerca dos trabalhos teóricos
e numéricos se constituem na principal motivação para a realização do presente trabalho.
Do ponto de vista analítico, são propostas soluções analíticas baseadas no método
do limite superior para o cálculo da carga de prensagem e das deformações plásticas
efetivas mais flexíveis com relação ao critério de plasticidade adotado e taxa de
deformação na descrição do comportamento de materiais processados após um único passe
de prensagem em temperatura ambiente. Além disso, buscando ordenar os diversos efeitos
associados à técnica PCEA, é feita uma classificação qualitativa da relevância destes
parâmetros sobre os modelos analíticos propostos, utilizando-se o método fatorial 2k.
Em relação à utilização da simulação computacional, são desenvolvidos modelos
numéricos bidimensionais e tridimensionais que utilizam a formulação de elementos finitos
para a obtenção, sob carregamento quase-estático, de resultados satisfatórios de carga e
deformação plástica efetiva após a prensagem a frio, por um único passe, de materiais
dependentes ou não dos efeitos de taxa de deformação. Além disso, são avaliadas também
as condições críticas de atrito que conduzem à condição de aderência e seus efeitos sobre a
distribuição homogênea das deformações plásticas efetivas.
3
Com base em sua motivação, este trabalho se divide em sete partes distintas. A
primeira parte apresenta, em detalhes, os objetivos do presente trabalho.
A segunda parte é destinada à apresentação e discussão das pesquisas realizadas
acerca dos chamados métodos de deformação plástica severa (DPS), desde a sua
descoberta até os trabalhos mais recentes, com maior aprofundamento dedicado à
prensagem em canais equiangulares (PCEA), visto ser o tema central do presente trabalho.
Por fim, se realiza uma discussão conclusiva com o intuito de apontar as limitações das
pesquisas já realizadas, especialmente as que tratam das análises teóricas e numéricas.
A terceira parte descreve os materiais e os métodos adotados no desenvolvimento
dos modelos analíticos e numéricos voltados ao estudo do processamento de materiais via
a técnica PCEA. A seção MATERIAIS mostra em detalhes os diversos materiais utilizados
no que se refere às suas origens e condições de ensaio para a obtenção das respectivas
curvas de encruamento. Na seção MÉTODOS aborda-se a descrição detalhada dos
experimentos e modelos teóricos e numéricos desenvolvidos ao longo do presente trabalho,
respectivamente. Ao final desta parte são descritas as análises realizadas bem como os
respectivos parâmetros utilizados.
A quarta parte compreende a apresentação e discussão referentes aos resultados
obtidos a partir dos modelos teóricos e numéricos desenvolvidos.
A quinta parte compreende os aspectos conclusivos relacionados a cada conjunto
de resultados obtidos na terceira etapa do trabalho buscando ressaltar os pontos de maior
relevância associados aos diversos tipos de análises realizadas.
A sexta parte diz respeito à continuidade do presente trabalho, com base nos
objetivos propostos e nas conclusões obtidas a partir dos resultados alcançados. Desta
forma, os trabalhos subseqüentes a este visam complementar o estudo de materiais
deformados via o método de prensagem em canais equiangulares.
A sétima parte é destinada à listagem das referências bibliográficas consultadas
durante o desenvolvimento deste trabalho. Esta listagem inclui os artigos científicos
essenciais ao método PCEA, bem como as pesquisas mais recentes sobre o tema. Além
disso, as obras consultadas ao longo do trabalho completam a lista de referências.
4
2. OBJETIVOS
Com base no capítulo 1. INTRODUÇÃO GERAL, os objetivos do presente
trabalho se dividem em:
2.1 OBJETIVO GERAL
Proposição de modelos teóricos analíticos e numéricos capazes de fornecer
previsões realísticas de carga e deformações plásticas efetivas oriundas do processamento
de materiais por um único passe de prensagem em canais equiangulares a frio.
2.2 OBJETIVOS ESPECÍFICOS
1) Modelamento analítico com a inclusão dos efeitos de critérios de escoamento e
viscoplásticos em soluções teóricas recentes destinadas à previsão da carga de prensagem;
2) Modelamento analítico com a inclusão dos efeitos de critérios de escoamento em
soluções teóricas recentes destinadas ao cálculo das deformações plásticas efetivas;
3) Classificação dos diversos parâmetros introduzidos em tais soluções analíticas, por
ordem de relevância, sobre os modelos teóricos propostos a partir do método de
planejamento de experimentos fatorial 2k;
4) Desenvolvimento de uma metodologia para o modelamento numérico da técnica PCEA
que permita obter resultados confiáveis de carga e deformações plásticas efetivas, sob a
forma quase-estática, para materiais dependentes ou não dos efeitos viscoplásticos.
5
3. REVISÃO BIBLIOGRÁFICA
Este capítulo é destinado à apresentação e discussão das pesquisas realizadas
acerca dos chamados métodos de deformação plástica severa (DPS), desde a sua
descoberta até os trabalhos mais recentes. Em primeiro lugar, são apresentados as idéias e
os primeiros estudos que definiram a origem destes métodos. Além disso, é mostrada a
mais recente classificação dos métodos DPS quanto à eficiência no refinamento
microestrutural e homogeneidade das microestruturas originadas após a conformação. Em
seguida, cada um dos métodos é tratado separadamente, sendo que o maior
aprofundamento da discussão é dedicado à prensagem em canais equiangulares (PCEA),
visto ser o tema central do presente trabalho. Nesse sentido, com relação à técnica PCEA, é
feita uma revisão sobre os princípios que o definem e os trabalhos experimentais, teóricos
e numéricos já realizados, desde sua invenção até os dias atuais. Por fim, destaca-se a
contribuição deste trabalho aos estudos relacionados à técnica PCEA, a partir de uma
análise crítica que aponta as limitações das pesquisas já realizadas, especialmente as que
tratam das análises teóricas e numéricas, tendo em vista o caráter do presente trabalho.
3.1 A ORIGEM DOS MÉTODOS DE DEFORMAÇÃO PLÁSTICA SEVERA
As primeiras idéias acerca da utilização do cisalhamento para o processamento de
materiais foram propostas por Bridgeman [8], ao combinar torção e compressão de discos
finos e demonstrar a existência de fortes efeitos da deformação plástica sobre as
propriedades físicas e mecânicas de diversos materiais. Assim, Richmond et al. [9]
consideraram pela primeira vez a otimização das operações de conformação, realizando
ensaios de cisalhamento puro em busca das condições “ideais” de extrusão e estiramento.
6
Este trabalho marcou o início do desenvolvimento dos chamados métodos de deformação
plástica severa (DPS), ou seja, métodos não-convencionais de deformação que se
caracterizam por transformar cisalhamento puro em operações ordinárias e efetivas de
produção.
Valiev et al. [3], avançaram ainda mais na caracterização dos métodos de DPS, no
que se refere às suas vantagens em relação aos processos tradicionais de conformação,
após reunirem em uma coletânea a grande maioria dos trabalhos já publicados sobre o
tema. Segundo estes autores, os métodos de deformação plástica severa se destacam por
produzirem materiais cujas nanoestruturas são formadas por estruturas ultrafinas de um
tipo granular contendo, principalmente, contornos de alto ângulo. O refinamento
microestrutural proporcionado pelos processos tradicionais de conformação, por outro
lado, origina materiais com estruturas que são subdivisões de um tipo celular que contém
contornos com meso-orientação de baixo ângulo. A partir do principio de refinamento
microestrutural induzido sobre o material deformado, estes autores classificaram a
deformação por torção, o forjamento múltiplo e a prensagem em canais equiangulares
como os mais importantes métodos de deformação plástica severa.
3.2 DEFORMAÇÃO POR TORÇÃO SOB ELEVADA PRESSÃO
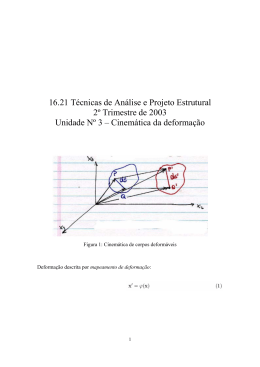
Segundo Valiev et al. [3], esta técnica se destina à obtenção de amostras sob a
forma de discos, como apresentado na Figura 1. Um lingote fabricado a partir do material a
ser deformado é soldado entre bigornas e elevados níveis de pressão são impostos pela
ação do punção. Em seguida, o suporte inferior é rotacionado e as forças de atrito entre as
superfícies em contato promovem a deformação da peça sob condições de cisalhamento.
Entretanto, por se tratar de lingotes, a ação do punção e a reação das camadas mais
externas do material evitam que a amostra seja destruída durante a conformação, já que seu
volume principal é deformado em condições de compressão quase-hidrostática.
7
Figura 1: Deformação por torção sob elevada pressão. Adaptado de Valiev et al. [3].
Após várias rotações, a deformação severa imposta ao material resulta em um
refinamento microestrutural similar na região central da amostra, ao passo que a
nanoestrutura processada se mostra homogênea ao longo da direção radial do disco. De
acordo com Valiev et al. [10], apenas uma rotação de 1/2 volta já induz níveis de
deformação capazes de conduzir a uma considerável mudança microestrutural do material.
Porém, para a formação de uma nanoestrutura homogênea são necessárias inúmeras
rotações. A técnica de deformação por torção não se destina somente ao refinamento
microestrutural. Os trabalhos de Valiev [11] e Alexandrov et al. [12-13] revelaram que este
método DPS pode ser aplicado com sucesso na consolidação de pós. Estes trabalhos
mostraram que a deformação sob elevada pressão, à temperatura ambiente, fornece
densidades próximas a 100% em amostras nanoestruturadas com geometrias de discos.
3.3 FORJAMENTO MÚLTIPLO
Esta técnica está associada à recristalização dinâmica e apresenta como princípio
básico múltiplas repetições de operações livres de forjamento, ou seja, tracionamentos da
amostra em diferentes eixos de aplicação da carga de deformação, conforme
esquematizado na Figura 2. Entretanto, a homogeneidade de deformações fornecida pelo
forjamento múltiplo é menor que aquela observada na deformação por torção.
8
(a)
(b)
(c)
Figura 2: Princípio do forjamento múltiplo: (a) forjamento e usinagem ao longo do
primeiro eixo de deformação, (b) ao longo do segundo eixo de deformação e (c) ao
longo do terceiro eixo de deformação. Adaptado de Valiev et al. [3].
3.4 PRENSAGEM EM CANAIS EQUIANGULARES
3.4.1 Definição e princípios da técnica PCEA
A prensagem ou extrusão em canais equiangulares, é um método de deformação
plástica severa destinado à produção de materiais ultrafinos com propriedades mecânicas
superiores. A técnica PCEA consiste na passagem de um tarugo lubrificado através de uma
matriz composta por dois canais de seções transversais idênticas. Os canais são conectados
e usualmente perfazem um ângulo Φ = 90º, conforme apresentado na Figura 3. No entanto,
para materiais de difícil conformação mecânica, por exemplo, titânio e suas ligas, este
ângulo da matriz pode variar entre 90 e 120º, de acordo com Segal [7]. O material é
prensado pela ação de uma ferramenta (punção) acoplada a uma prensa de alta pressão e,
ao atravessar a região de interseção dos canais, é deformado continuamente em condições
muito próximas ao cisalhamento simples.
9
Figura 3: Princípio da prensagem em canais equiangulares: o ângulo β define o ângulo de
abertura dos raios de adoçamento. Adaptado de Furukawa et al. [14].
Segundo Srinivasan [15], a vantagem desta técnica é o seu caráter de
continuidade, ou seja, as amostras podem ser repetidamente deformadas. Desta maneira,
níveis cada vez maiores de deformações permanentes são impostos ao material,
acompanhados pela elevação de suas propriedades mecânicas de interesse, tal como
resistência mecânica ao escoamento plástico. Os múltiplos passes de prensagem, sugeridos
primeiramente por Segal [6], constituem-se em alternativas para o desenvolvimento de
estruturas e texturas num mesmo material por meio da ativação dos planos e direções de
cisalhamento. Sendo assim, são apresentadas a seguir algumas situações possíveis de
ativação dos planos e direções de cisalhamento.
3.4.1.1 Rota A
Nesta rota, o sentido de deformação do tarugo é mantido a cada passe, como pode
ser observado na Figura 4. Como resultado, a distorção do material é continuamente
aumentada após cada ciclo.
Figura 4: Desenho esquemático mostrando a metodologia de prensagem referente à rota A.
10
A microestrutura obtida assemelha-se àquela obtida num processo de laminação a
frio onde os grãos tornam-se extremamente alongados em comparação ao material de
partida, vide evolução microestrutural mostrada na Figura 5 para o Ni puro em função do
número de passes, como reportado por Segal [6].
(a)
(b)
(c)
(d)
Figura 5: Ni puro prensado por meio da rota A: (a) condição inicial; (b) após um passe,
(c) após dois passes e (d) após três passes. Adaptado de Segal [6].
3.4.1.2 Rota C
Nesta rota, o tarugo é girado a 180º em torno de seu eixo em passes subseqüentes,
vide esquema na Figura 6, na qual o tarugo é deformado somente em números ímpares de
ciclos. Os passes de números pares caracterizam o retorno às formas originais do tarugo,
em razão da presença das deformações redundantes. Os grãos obtidos são equiaxiais e
uniformes, de acordo com Segal [6].
A Figura 7 mostra as microestruturas provenientes da submissão do Ni puro à
prensagem em três ciclos por meio da rota C, também obtidas por Segal [6]. Ainda
segundo Segal [6], esta rota de processamento produz uma considerável rotação
permanente para grãos e subgrãos e forma uma textura resistente por causa do rearranjo de
sistemas cristalográficos e fácil deslizamento ao longo do plano e da direção de
cisalhamento, após múltiplos passes.
11
Figura 6: Desenho esquemático mostrando a metodologia de prensagem referente à rota C.
(a)
(b)
Figura 7: Amostras de Ni puro prensadas pela rota C. (a) após dois passes e
(b) após três passes. Adaptado de Segal [6].
3.4.1.3 Rotas B
Este esquema de processamento implica na rotação de 90º em torno do eixo do
tarugo e subdivide-se nas rotas BA e BC, em função do sentido de rotação do tarugo,
conforme pode ser visto em detalhes na Figura 8. A rota BA caracteriza-se por rotações
alternadas em 90º, ou seja, no segundo passe o tarugo é girado no sentido anti-horário e no
passe seguinte no sentido horário. Segal [6] observou que as microestruturas provenientes
deste processamento têm a forma de fibras e o material apresenta textura axial. Por outro
lado, a rota BC compreende rotações no tarugo a 90º, porém apenas no sentido horário e
este fato implica no aparecimento das chamadas deformações plásticas redundantes que
são responsáveis pelo retorno à microestrutura original, como observado na rota C de
processamento. Da mesma forma, as microestruturas obtidas apresentam grãos equiaxiais.
12
(a)
(b)
Figura 8: Esquema de processamento das rotas B. (a) rota BA e (b) rota BC.
De acordo com Valiev et al. [16], as rotas de processamento se diferenciam
quanto à ativação de sistemas de deslizamento específicos durante cada ciclo de prensagem
efetuado sobre o material. A Figura 9 apresenta os diferentes sistemas de deslizamento
associados às rotas A, B e C e as respectivas distorções provocadas sobre os planos
cisalhantes X, Y e Z ao longo de oito passes de prensagem. No caso da rota C, o
cisalhamento é imposto ao material sobre o mesmo plano quando este atravessa a zona de
deformações localizada na região de interseção dos canais da matriz. Isto explica o
surgimento das deformações redundantes, responsáveis pelo retorno microestrutural à
configuração inicial observada a cada passe de número par. Da mesma forma, ao ser
deformado por meio da rota BC, o material mostra um regresso à microestrutura inicial
promovido pelas rotações impostas ao tarugo, conforme detalhado na Figura 8b. Assim, o
deslizamento ocorrido no primeiro passe é anulado durante o terceiro ciclo de prensagem,
bem como o quarto passe elimina o deslizamento observado ao longo do segundo passe.
Por outro lado, as rotas A e BA não apresentam deformações redundantes. No que se refere
à rota A, existem dois planos cisalhantes que se interceptam a um ângulo reto e são
responsáveis pela deformação plástica do material.
A rota BA, por sua vez, se caracteriza por atribuir deformações permanentes à
amostra pela ação de quatro planos de cisalhamento interceptados a 120°.
Pelas distorções causadas sobre um elemento cúbico por sistemas de deslizamento
atuantes em cada uma das rotas de processamento, fica claro que a geometria original é
recuperada a cada dois passes de prensagem via a rota C e a cada quatro pela rota BC. Por
outro lado, estas distorções se tornam mais severas para as rotas A e BA. Todavia, o
elemento cúbico não se deforma sobre o plano Z quando prensado via as rotas A e C.
13
(a)
(b)
Figura 9: Prensagem segundo as rotas A, B e C: (a) sistemas de deslizamento em relação
aos eixos X, Y e Z em passes consecutivos e (b) distorções observadas em elementos
cúbicos submetidos a oito passes de prensagem. Adaptado de Valiev et al. [16].
3.4.2 Estudos sobre o processamento de materiais via a técnica PCEA
3.4.2.1 Caracterização experimental
As observações experimentais sobre o comportamento de materiais deformados
por meio da prensagem em canais equiangulares se intensificaram na década de 1990,
precisamente a partir do ano de 1996. A causa desta motivação foi o trabalho publicado por
Segal [7], no qual se destacou a eficácia da técnica PCEA em atribuir elevados níveis de
deformação plástica em amostras de níquel puro, elevando suas propriedades mecânicas.
Este trabalho elucidou o caráter de continuidade associado a este processo de conformação
ao discutir as mudanças microestruturais decorrentes das rotas de processamento A e C.
Em contrapartida, ficou evidenciado a necessidade de serem investigados os
comportamentos de outros materiais em plasticidade severa já que este método poderia
transformar o cisalhamento simples em operações industriais, principalmente para a
formação de texturas específicas, promovendo o desenvolvimento da tecnologia de
materiais avançados.
14
Os estudos de caráter experimental, desencadeados a partir das idéias propostas
por Segal [7], podem ser divididos, quanto aos seus objetivos centrais, em duas classes
distintas, a saber, (1) análises da relação entre as rotas de processamento e o refinamento
microestrutural e (2) melhoria de propriedades mecânicas. Em segundo lugar, se observam
estudos dos efeitos das condições de atrito e taxa de deformação sobre propriedades como
tensão de escoamento e expoente de encruamento do material deformado.
Em relação à primeira classe de pesquisas, Wang e colaboradores [17] avaliaram a
liga Al-3%Mg em 4 ciclos de prensagem numa matriz com canais interceptados a 90°
verificando um elevado refinamento estrutural composto por grãos com contornos de alto
ângulo para temperaturas entre 443K e 803K. Furukawa et al. [18] empregaram 4 ciclos de
prensagem para uma liga de alumínio Al-5,5%Mg-2,2 Li-0,12% em uma matriz de 90º.
Estes autores confirmaram as observações de Wang et al. [17] ao obterem uma
microestrutura estável a 700K formada por grãos ultrafinos. Além disso, observaram a
queda da dureza em função do aumento da temperatura de recozimento das amostras
deformadas.
Valiev [19] observou que além da ligas de alumínio Al - 4%Cu - 0,5% Zr e
Zn - 22% Al, outros materiais como as ligas à base de chumbo e estanho (Pb - 62% Sn), Ti
e Cu puros também apresentaram estruturas nano e sub-microcristalinas com contornos de
alto ângulo, obtidas após um total de 15-20 passes de prensagem. Contudo, estes materiais
apresentaram uma grande heterogeneidade na região dos contornos de grão. Em relação às
propriedades mecânicas, verificou-se também o papel primário desempenhado pela
temperatura de recozimento sobre o tamanho de grão e as propriedades mecânicas como a
tensão de escoamento, dureza e resistência à tração.
A Figura 10 mostra a influência da temperatura de recozimento sobre o
comportamento mecânico do Ti puro. De fato, os valores de microdureza (curva 2)
mostram pequena variação no intervalo para temperaturas de recozimento até 250ºC, em
conseqüência do mesmo comportamento observado na curva 1 para o tamanho de grão d.
A partir de 300ºC o abrupto crescimento de grãos causou uma queda acentuada de dureza.
Por outro lado, o aumento do tamanho de grãos a partir de 300º C promoveu a
queda simultânea do limite de escoamento e da resistência à tração já que grãos maiores
conduzem ao aumento da ductilidade do material.
15
Figura 10: Dependência entre tamanho de grão e propriedades mecânicas do titânio
puro com a temperatura de recozimento. Adaptado de Valiev [19].
A sensibilidade das propriedades mecânicas e tamanho de grão com a temperatura
de recozimento (200-350°C) foi também reportada por Markushev et al. [20], para a liga de
alumínio Al-1560. Ainda, o trabalho de Pithan et al. [21] onde amostras da liga Al-5056
foram deformadas segundo a rota C numa matriz com Φ = 90° em 8 passes. Estes autores
observaram que as amostras deformadas em temperaturas próximas a 200°C, apresentaram
um desenvolvimento de microestruturas controlado pela recuperação dinâmica.
Reduzindo-se esta condição térmica o material apresentou microestruturas refinadas sob a
forma de finas fibras.
Os estudos do refinamento microestrutural promovido pelas rotas de
processamento e as alterações em propriedades mecânicas foram também conduzidos em
outros materiais. Assim, destaca-se o trabalho de Gibbs et al. [22] voltado para a análise da
formação de texturas em amostras de ferro puro prensadas a partir das rotas A, B e C
(4 passes) em uma matriz com canais interceptados a 90°. Verificou-se que a rota A
forneceu textura similar à obtida ao se laminar o material a frio. A rota C se caracterizou
pelo retorno à microestrutura inicial, em decorrência do aparecimento de deformações
redundantes. Por fim, as rotas B originaram materiais com texturas típicas da estampagem.
O aço baixo carbono, contendo 0,15% C foi utilizado nos trabalhos desenvolvidos
por Shin e colaboradores [22-24]. As rotas A e C foram utilizadas em conjunto com uma
matriz cuja interseção de canais perfazia um ângulo de 90°. Estes autores observaram a
existência de uma microestrutura estável em temperaturas de recozimento entre 683-783K
formada por grãos ultrafinos após 4 passes de prensagem assumindo-se a rota C.
16
Além disso, o refinamento microestrutural se mostrou mais significativo após o primeiro
passe, ao passo que o aparecimento de contornos de alto ângulo aumentou
progressivamente com o número de ciclos de prensagem. Em relação às propriedades
mecânicas, os testes experimentais revelaram uma elevação considerável da resistência
mecânica em detrimento do alongamento total também após o primeiro passe. A rota A foi
responsável por um leve aumento da resistência à tração, em comparação à rota C,
conforme apresentado na Tabela 1.
Tabela 1 Efeitos do número de passes e rotas (A e C) sobre a resistência à tração (RT) e
alongamento de aço baixo carbono. Adaptado de Shin et al. [22].
Condição
Material como recebido
1 passe
2 passes (rota A)
2 passes (rota C)
RT (MPa)
450
750
805
800
Alongamento (%)
22
15
13
13
Por outro lado, Zhu et al. [25] reportaram a existência de contradições sobre a
indicação da rota de processamento mais eficiente no refinamento microestrutural e na
melhoria de propriedades mecânicas, uma vez que os efeitos da deformação acumulada e
ativação de planos cisalhantes na interpretação de observações experimentais foram
considerados de forma superficial. Estas contradições se referem aos estudos realizados por
Iwahashi et al. [26-27], Prangnell et al. [28] e Furukawa et al. [29], nos quais se utilizaram
o alumínio e suas ligas.
Prangnell et al. [28] processaram uma liga de Al (Al-3%, Mg-0,2% e Zr-0,2%)
utilizando as rotas A, B e C numa matriz com ângulo Φ = 120º. Por meio da técnica de
difração de elétrons retroespalhados de alta resolução foi medida a orientação dos grãos e
os resultados obtidos mostraram que a rota A foi mais efetiva no refinamento de grãos,
enquanto as rotas C, BC e BA foram menos efetivas. A justificativa dada para a eficiência
da rota A foi a ausência de deformações plásticas redundantes, o que não acontece quando
se utilizam as demais rotas de processamento, com exceção da rota BA. É importante
ressaltar que esta justificativa, ou seja, a teoria de deformações redundantes concordou
plenamente com as observações das microestruturas obtidas para esta liga. Entretanto, esta
teoria não explica a maior eficiência da rota BC sobre a rota BA, uma vez que a rota BA não
apresenta deformações plásticas redundantes.
17
Iwahashi et al. [26-27] processaram Al puro em uma matriz com Φ = 90º,
utilizando-se as rotas A, BC e C. Entretanto, observaram que a rota BC foi mais efetiva que
a rota A e apresentou pequena influência no refinamento de grãos. Para explicar estas
observações experimentais, Furukawa et al. [29] analisaram a distorção de um elemento
cúbico causada pela deformação das diversas rotas da técnica PCEA. As conclusões
obtidas mostram que as rotas BC e C foram mais eficientes que as rotas A e BA, pois as
deformações plásticas redundantes permitiram que o elemento cúbico fosse reconstituído
por 4 passes de rota BC e 2 passes de rota C, ao passo que nas rotas A e BA ocorre
continuamente a deformação do cubo. Posteriormente, Iwahashi et al. [26-27]
consideraram as relações de orientação dos planos de cisalhamento de passes consecutivos
para cada uma das rotas da técnica PCEA.
Com base nestas contradições, Zhu et al. [25] analisaram os resultados disponíveis
na literatura e investigaram os mecanismos fundamentais do refinamento de grãos,
concentrando esforços na interação dos planos de cisalhamento com a estrutura cristalina e
a formação das texturas. Devido à considerável quantidade de informações sobre o Al e
suas ligas, estes materiais foram utilizados para a avaliação do comportamento do plano de
alongamento dos grãos frente ao plano de cisalhamento por meio do ângulo θ entre estes e
da direção de alongamento dos grãos, vide esquema na Figura 11. Segundo
Iwahashi et al. [26-27], a rota BC foi mais eficiente no refinamento de grãos porque após
passes ímpares manteve a mesma direção de alongamento dos grãos (26º). Ademais, a
relação de orientação manteve-se constante (θ = 71,6º) e próxima ao valor de 70,5º que é o
ângulo entre duas faces de um tetraedro {111}, ativando o sistema de deslizamento sobre o
plano cisalhante subseqüente e facilitando a deformação cisalhante.
Em relação à rota BA, embora apresente o mesmo ângulo entre dois planos
cisalhantes adjacentes, o valor de β decresce continuamente após o primeiro passe, o que
não permite que seja mantido o valor de θ igual a 70,5º. Por este motivo a rota BA torna-se
menos eficiente no refinamento de grãos, embora não apresente deformações plásticas
redundantes. Para a rota A, o ângulo θ decresce continuamente nos passes subseqüentes e
esta rota, analogamente à rota BA, torna-se pouco eficaz no refinamento de grãos.
18
A rota C se mostrou mais eficaz no refinamento de grãos que a rota A somente
para Φ = 90º, ou seja, quando a interseção dos canais é feita a 120º existe a possibilidade
de reversão do acúmulo de discordâncias e textura gerada quando as deformações
cisalhantes impostas ao material são menores. Assim, as análises realizadas os levaram
Zhu et al. [25] a concluir que a interação do plano de cisalhamento com a estrutura
cristalográfica desempenha um papel primário no refinamento dos grãos ao passo que o
papel da deformação acumulada é secundário.
Figura 11: Orientação entre o plano de alongamento dos grãos (1°passe) e o plano
cisalhante do segundo passe para as rotas BC ou BA. Adaptado de Zhu et al. [25].
Apesar dos esforços de Zhu et al. [25] em indicar a rota de processamento mais
eficaz em termos de refinamento microestrutural e melhorias de propriedades mecânicas,
esta questão se mantém como objetivo principal das pesquisas mais recentes acerca da
prensagem em canais equiangulares. Neste contexto, destacam-se os trabalhos de
Dalla Torre e diversos colaboradores [30-31], nos quais foram avaliadas as influências da
microestrutura e desorientação sobre as propriedades mecânicas do cobre puro. Para tanto,
a rota BC foi utilizada durante a prensagem do material em um total de 16 passes em
temperatura ambiente por meio de uma matriz com Φ = 90°. A microestrutura resultante é
composta por contornos lamelares com grãos equiaxiais à medida que o número de passes
aumenta, vide Figura 12a. Por outro lado, a resistência à tração do material atingiu o seu
valor máximo após 4 passes de deformação. Em seguida, foi constatada uma queda desta
propriedade a partir do 5º passe em função da recristalização dinâmica (Figura 12b).
19
(a)
(b)
Figura 12: (a) evolução microestrutural observada durante a prensagem de cobre puro e
(b) curvas tensão-deformação após cada passe. Adaptado de Dalla Torre et al. [30].
Recentemente, Xu et al. [32] analisaram a homogeneidade de dureza observada
após a prensagem de amostras de Al puro e da liga Al 6061. Os tarugos foram deformados
a partir da rota BC em um total de 8 passes, em temperatura ambiente. Em relação à
geometria da matriz, o ângulo de interseção dos canais foi mantido constante e igual a 90°.
Todavia, os efeitos da adoção de raios de adoçamento externo sobre as propriedades
mecânicas dos materiais considerados foram investigados ao se adotarem os valores de 0°
e 20° para o ângulo de abertura β esquematizado na Figura 13a. Em ambos os materiais foi
observado um elevado aumento da dureza após o primeiro passe, conforme Figura 13b.
Entretanto, o alumínio puro exibiu uma saturação a partir do quarto passe devido à alta
energia de falha de empilhamento associada com elevadas taxas de encruamento e
recuperação. A liga Al 6061 é caracterizada por baixa energia de falha de empilhamento e
taxas de encruamento e recuperação inferiores. Portanto, para atingir a saturação este
material necessita de um número maior de passes de prensagem.
20
(a)
(b)
Figura 13: (a) esquema da técnica PCEA com destaque para o ângulo β e (b) valores
médios de dureza referentes ao Al puro e à liga Al 6061. Adaptado de Xu et al. [32].
A segunda classe de investigações experimentais é representada pela influência
das condições de atrito e taxa de deformação sobre a homogeneidade de deformações
plásticas como, por exemplo, nos trabalhos de Stolyarov et al. [33] e La et al. [34] a partir
de tarugos de Ti puro processados a 450°C por meio da rota BC em 8 passes. Os resultados
obtidos por La et al. [34] confirmaram as observações de Stolyarov et al. [33], já que
houve reduções do coeficiente de atrito estático e da carga de prensagem, provocadas pelo
refinamento microestrutural e o aumento da velocidade de prensagem, como mostra a
Figura 14.
(a)
(b)
Figura 14: Variação do coeficiente de atrito com (a) carga de prensagem, para a
velocidade de 0,5 m/s e (b) velocidade para a carga de 20 N. Adaptado de La et al. [34].
21
Os efeitos de taxa de deformação sobre as propriedades mecânicas foram
estudados por May et al. [35]. Nestes trabalhos foram utilizadas amostras de alumínio puro
processadas à temperatura ambiente em uma matriz com Φ = 90° por meio de múltiplos
passes de prensagem utilizando a rota BC. Depois de deformadas, as amostras foram
submetidas a ensaios de compressão em temperaturas entre 25°C e 250°C variando-se a
taxa de deformação no intervalo 10-3 e 10-5 s-1. Em primeiro lugar, o refinamento
microestrutural promoveu um aumento do limite de escoamento do material tanto à
temperatura ambiente como a 200ºC, como mostra a Figura 15a. Entretanto, os resultados
obtidos para o alumínio ultrafino (em vermelho) mostraram uma baixa capacidade de
encruamento seguida por um comportamento anormal caracterizado pela alternância da
tensão de escoamento quando a taxa de deformação aplicada aumenta ou diminui em uma
ordem de grandeza. May et al. [35] atribuíram estes aspectos aos efeitos de envelhecimento
dinâmico por deformação associado ao aprisionamento de discordâncias ou contornos de
subgrãos causado por átomos de impureza. Por outro lado, o material composto por grãos
maiores exibiu considerável capacidade de endurecimento por deformação representado
pelas monotônicas crescentes em azul mostradas na Figura 15a.
O aumento da temperatura de ensaio, por sua vez, promove a elevação da
sensibilidade à taxa de deformação para ambos os materiais, conforme apresentado na
Figura 15b. Entretanto, o alumínio com microestrutura composta por grãos ultrafinos
mostrou maior dependência com a taxa de deformação quando comparado ao dotado de
grãos maiores. Estes aspectos se tornam mais evidentes na Figura 15c, na qual é
relacionada à dependência entre microestrutura, temperatura de ensaio e sensibilidade à
taxa de deformação. Desta forma, May et al. [35] evidenciaram que a sensibilidade do
alumínio ultrafino aumenta em níveis mais baixos de temperatura quando comparada à
microestrutura caracterizada pela presença de grãos maiores. Assim, para cada valor de
temperatura a sensibilidade do Al ultrafino se mostrou maior que a do Al recozido, até que
para 250ºC o primeiro material atingiu um nível próximo à condição de deformação
superplástica, ou seja, para valores elevados do expoente de sensibilidade à taxa de
deformação, como é no caso em que s = 0,25.
22
(a)
(b)
(c)
Figura 15: Dependência da tensão de escoamento do Al puro com (a) temperatura de
ensaio (b) taxa de deformação e (c) relação entre s e n e a temperatura de prensagem.
Adaptado de May et al. [35].
3.4.2.2 Modelos teóricos
Neste conjunto de trabalhos, o foco central é a proposição de soluções analíticas
capazes de fornecer previsões cada vez mais realísticas de carga (força ou pressão) e
deformações plásticas efetivas impostas ao material durante a prensagem/extrusão em
canais equiangulares. Segundo Semiatin et al. [36], estes trabalhos podem ser classificados,
quanto à escala de modelamento, em macroscópicos ou mesoscópicos.
23
A Figura 16 mostra esquematicamente a classificação das contribuições teóricas.
Em escala macroscópica, os trabalhos são subdivididos quanto à abordagem utilizada para
a formulação das soluções analíticas. Assim, podem ser encontradas soluções puramente
geométricas, nas quais se avaliam apenas os efeitos de geometria da matriz sobre as
previsões de carga e deformações plásticas efetivas e soluções que empregam ora o método
do limite superior (MLS) ora o método de linhas de deslizamento (MLD), os quais incluem
os efeitos de geometria, tribologia e encruamento definido pelo critério de plasticidade
isotrópico de von Mises.
Em escala mesoscópica, são propostos modelos para previsão de texturas cuja
ênfase é mostrar a influência de incrementos de deformação induzidos ao material nas
superfícies de entrada e saída da zona de deformação sobre a evolução da textura quando
sucessivos passes de prensagens são atribuídos ao material. Para tanto, são consideradas as
condições mais severas de processamento, ou seja, os canais da matriz interceptados a 90º
e a utilização da rota A.
PCEA – classificação das pesquisas teóricas quanto à escala de modelamento
Macroscópica
Carga e deformação plásticas efetivas
Soluções
geométricas
Efeitos de
geometria da matriz
Mesoscópica
Previsão de texturas a partir de modelos
baseados em plasticidade policristalina
Soluções:
MLS e MLD
Modelos cinéticos:
Geração e aniquilamento de discordâncias
Efeitos de
geometria da matriz,
tribologia e plasticidade
Figura 16: Classificação dos trabalhos teóricos reportados na literatura quanto à escala
de modelamento das previsões de pressão e deformação oriundas da técnica PCEA.
24
- Soluções analíticas baseadas no método do limite superior (MLS)
Os estudos teóricos para o estabelecimento de soluções analíticas da carga
necessária à prensagem e a deformação plástica originadas da prensagem em canais
equiangulares foram iniciados por Segal [6]. Em uma matriz desprovida de raios de
adoçamento, vide detalhes na Figura 17 e, a partir do método do trabalho ideal, a pressão
(p) exercida pelo punção sobre a superfície superior do tarugo é calculada por:
p
2
=
cotg (Φ / 2)
σy
3
(1)
Na Equação (1) σy denota o limite de escoamento em tração uniaxial enquanto que γ é a
distorção angular necessária para transformar o elemento quadrado abcd em a’b’c’d’,
conforme esquema mostrado na Figura 17. Além disso, foi sugerido o valor total de
deformação plástica efetiva imposta ao material, após N ciclos de prensagem ( ε N ):
ε N = N∆ε i
(2)
onde ∆εi denota o incremento de deformação plástica atribuído ao material a cada passe de
prensagem.
Figura 17: Extrusão em canais equiangulares destacando a deformação do elemento abcd
em condições de cisalhamento simples. Adaptado de Segal [6].
25
Iwahashi et al. [37] apresentaram melhorias à solução destinada ao cálculo das
deformações plásticas efetivas. Estes autores apontaram que a ausência de adoçamento na
interseção externa dos canais poderia causar uma curvatura do material a um determinado
ângulo Ψ. Nesse sentido, levaram em conta três casos distintos, ou seja, a condição em que
a região de interseção externa dos canais se manteve completamente preenchida pelo
material (Ψ = 0°), um caso intermediário em que o material apresentou uma leve curvatura
(0º ≤ Ψ ≤ π - Φ) e o caso mais extremo no qual o dobramento do material foi mais
acentuado (Ψ = π - Φ). As situações mencionadas são mostradas na Figura 18.
Figura 18: Comportamento do material durante a deformação via PCEA. (a) Ψ = 0°;
(b) 0º ≤ Ψ ≤ π - Φ e (c) Ψ = π - Φ. Adaptado de Iwahashi et al. [37].
Assim, para cada um dos casos apresentados na Figura 18, tem-se:
a' q
= 2 cotg (Φ / 2) → Ψ = 0°
qd '
−1  Φ + Ψ 
a' u
Φ+Ψ
γ=
= 2 cotg 
 + Ψ sen 

d' u
 2 
 2 
rc'
γ=
=Ψ →
Ψ=π−Φ
rb'
γ=
→
0° ≤ Ψ ≤ π − Φ
(3)
26
A deformação plástica efetiva de von Mises após N passes foi determinada para o
caso em que 0º ≤ Ψ ≤ π - Φ, uma vez que a solução correspondente para o cálculo de γ se
reduz aos casos limites, ou seja:
N 
 1 
Φ +Ψ
 Φ + Ψ 
ε=N
γ =
 2 cotg  2  + Ψ cossec  2  
3




 3 
(4)
A inclusão dos efeitos de encruamento e do raio de adoçamento externo sobre as
previsões analíticas de pressão foi apresentada por Alkorta et al. [38]. A geometria da
matriz e os respectivos campos de velocidade utilizados por estes autores são mostrados na
Figura 19a. Neste trabalho, os efeitos das condições de atrito sobre as previsões de pressão
não foram considerados e o encruamento do material foi definido pelo critério de
von Mises associado à lei de Hollomon.
Figura 19: Análise da técnica PCEA pelo método do limite superior em condições de
deformação plana. Adaptado de Alkorta et al. [38].
A partir dos hodógrafos de velocidade apresentados na Figura 19, as previsões de
pressão normalizada pelo limite de escoamento em tração uniaxial (p/σy) são obtidas por:

p
K
 Φ +β 
2 cotg 
=
 + β

σy
3 ( n + 1) 
 2  
( n +1)
(5)
onde K e n denotam o coeficiente de resistência da lei de potência de Hollomon e o
expoente de encruamento.
27
A deformação plástica efetiva corrigida pelo critério de von Mises é obtida pela
soma das contribuições de distorção angular nas regiões A, B e C definidas na Figura 19a,
ou seja:
ε=
1 
 Φ +β 
 2 cotg  2  + β
3 

 
(6)
Alkorta et al. [38] demonstraram analiticamente e comprovaram pela simulação
computacional baseada no método dos elementos finitos (MEF) que um decréscimo de
pressão normalizada é obtido aumentando-se o ângulo β ou o expoente de encruamento.
Ao mesmo tempo, observaram a forte dependência da pressão normalizada com o ângulo
de interseção dos canais (Φ), como conseqüência do comportamento apresentado pelas
deformações plásticas efetivas. Estes resultados são apresentados na Figura 20.
(a)
(b)
(c)
Figura 20: (a) efeitos de β e Φ sobre p/σy; (b) sensibilidade de p/σy ao expoente de
encruamento e (c) dependência da deformação plástica efetiva com a geometria da
matriz. Adaptado de Alkorta et al. [38].
28
Pérez [39], utilizando o método do limite superior, propôs a primeira solução
analítica para o cálculo da pressão de prensagem introduzindo a sua dependência com as
condições de atrito para materiais perfeitamente plásticos. Esta solução apresentou um
segundo avanço em relação às demais, ou seja, a geometria da matriz era composta por
raios de adoçamento iguais. A Figura 21 apresenta a referida geometria e o respectivo
hodógrafo de velocidades.
Figura 21: Matriz de prensagem composta por raios de adoçamento (R) iguais e o
respectivo hodógrafo de velocidades. Adaptado de Pérez [39].
A partir da Figura 21, a solução pelo método do limite superior para a pressão
normalizada (p/σy) obtida por Pérez [39] tem a seguinte forma:
p
2
=
σy
3


Rm
Φ m
(1 + m) cotg  2  + L (l i + l o ) + L (π − Φ )
 


(7)
onde m, L, li, e lo definem o fator de atrito de Tresca, a largura dos canais da matriz e os
comprimentos instantâneos do tarugo nas superfícies de entrada e saída da zona de
deformação, respectivamente definidas pelas linhas 1 e 2 ilustradas na Figura 21.
29
Em ausência de atrito, a Equação (7) se reduz à solução obtida por Segal [6], vide
Equação (1). As previsões analíticas de pressão normalizada e (ε) foram comparadas às
obtidas numericamente pelo MEF, para a liga de alumínio Al 5083. De fato, Pérez
observou o decréscimo de (p/σy) com o aumento de Φ, como já havia sido reportado
anteriormente por Alkorta et al. [38]. Por outro lado, a solução proposta permitiu observar
que o aumento dos raios de adoçamento mostrou um acréscimo de pressão, ou seja,
matrizes com raio de adoçamento interno maior que zero demandam níveis de carga
elevados para a prensagem de tarugos. Em relação ao atrito, a simulação computacional
verificou a consistência da Equação (7), uma vez que a força de prensagem se elevou para
valores maiores de m. Estes resultados são apresentados na Figura 22.
(a)
(b)
Figura 22: (a) sensibilidade de (p/σy) às variações de R e Φ e (b) efeito das condições de
atrito sobre a pressão determinado via MEF. Pe e Pe_frict se referem a m = 0 e 0,10
respectivamente. Adaptado de Pérez [39].
Em seguida, Pérez [40] propôs uma solução analítica para matrizes com diferentes raios de
adoçamento, vide matriz apresentada na Figura 23, na qual se destaca a presença de raios
interno (Rint) menor que o externo (Rext). Pérez [40] obteve a expressão para o cálculo do
ângulo β em função dos demais parâmetros geométricos:


0,5 ( R ext − R int )
β = 2 tg −1 

2
 L + ( R int − R ext ) cos (Φ / 2) 
(8)
30
Portanto, o ângulo β passou a ser calculado ao invés de se constituir em um dado
de entrada no cálculo da deformação efetiva (ε) . A estimativa deste parâmetro é
determinada a partir do cisalhamento necessário à transformação do elemento quadrado
abcd em um elemento distorcido a’b’c’d’ (Figura 23), corrigido pelo critério de von Mises:
ε=
γ
1 
Φ+β
β
 Φ + β 
=
 2 cotg  2  + (π − Φ) tg  2  cossec  2 
3
3


 


(9)
Figura 23: Matriz composta por raios de adoçamento distintos. Adaptado de Pérez [40].
As Equações (8) e (9) prevêem elevados níveis de deformação plástica efetiva
quando Rint se aproxima de Rext, como mostra a Figura 24. Por outro lado, sabe-se que este
comportamento está associado ao acréscimo da pressão normalizada apresentado pela
Figura 22a.
Figura 24: Previsões de ε para geometrias distintas de matriz. Adaptado de Pérez [40].
31
As influências das condições de atrito e raio de adoçamento interno sobre a carga
de prensagem foram também analisados por Altan et al. [41]. Com bases no método do
limite superior, estes autores consideraram os efeitos causados pelo desenvolvimento de
uma superfície de zona morta vazia, superfície Γm na Figura 25, igualmente observada nos
experimentos conduzidos por Shan et al. [42]. Altan et al. [41] utilizaram uma liga Al-Zn
aproximada para a condição perfeitamente plástica descrita pelo critério de von Mises.
Neste modelo, a taxa de energia dissipada durante a deformação do material no interior da
zona de deformação é dada por:
.


 ξ   ξ

W total = L2 V0 κ   2 + (1 + m )     − 2 δ  + 2 (1 + m ) tg δ 
L
2
  



(10)
onde ξ define a origem do sistema de coordenadas (O) e o centro do raio de adoçamento ao
passo que δ é o ângulo formado entre os eixos coordenados (x,y) e as superfícies de
entrada Γi e saída Γo, respectivamente. Ainda, κ denota a tensão de escoamento em
cisalhamento.
Em seguida, a solução para a força de prensagem P para um tarugo de altura H e
largura L é obtida pela contribuição de todas as parcelas de dissipação de energia por:

 ξ   π

P = L2 κ   2 + (1 + m )     − 2 δ  + 2 (1 + m ) tg δ
L
2
  



 + 4m L H κ

Figura 25: Geometria de deformação do modelo proposto por Altan et al. [41].
(11)
32
A partir da minimização da Equação (10), Altan et al. [41] estabeleceram a
condição de formação da zona de deformação em função tanto de parâmetros de geometria
da matriz (ξ/L) e quanto das condições de atrito (m):
m≥
ξ L
2 − (ξ L )
(12)
onde o ângulo δ é calculado por:
 (1 − m ) + (1 + m ) (ξ L) 
δ = tg −1 

(1 + m )


(13)
Esta condição apresentada no gráfico da Figura 26a indica, indiretamente, o
aparecimento da zona morta em função do estabelecimento da zona de deformação. Por
outro lado, os autores verificaram o aumento da zona de deformação em função do
decréscimo do ângulo δ para valores elevados de ζ ou de m, como mostra a Figura 26b.
(a)
(b)
Figura 26: (a) relação entre o fator de atrito, raio interno e formação da zona de
deformação e (b) tamanho da zona de deformação em função do fator de atrito.
Adaptado de Altan et al. [41].
Por fim, ao considerarem que o forjamento prevalece nos primeiros estágios da
técnica PCEA, Altan et al. [41] obtiveram uma solução analítica para a força de extrusão
que permitiu uma idealização da curva de prensagem do material, ou seja:

mL 
P = L2 σ y 1 +

2H 3

(14)
33
A curva idealizada foi validada ao ser comparada aos resultados obtidos
experimentalmente, o que pode ser apreciado nas Figuras 27a e 27b. Ambas mostraram
zonas de domínio do atrito estático (regiões A e B) e o deslocamento do tarugo em direção
ao segundo canal promoveu um pico de força em condições dinâmicas de atrito (ponto C).
Em seguida, a deformação contínua e estabelecida causou o decréscimo de força (D a E).
(a)
(b)
Figura 27: Curvas carga-deslocamento (a) real e (b) teórica. Adaptado de Altan et al.[41].
Eivani et al. [43] propuseram a primeira solução analítica que permitiu investigar
de forma conjunta a influência de parâmetros como geometria da matriz, critério de
escoamento e tribologia. O método do limite superior, por possibilitar a inclusão dos
efeitos de encruamento, atrito e geometria do ferramental em sua formulação matemática,
foi utilizado pelos autores no desenvolvimento da expressão para o cálculo da carga de
processamento. Para tanto, consideraram a geometria de matriz e os campos de velocidades
similares aos previamente adotados por Alkorta et al. [38], como mostra a Figura 28. Ao
estabelecerem o método do limite superior a partir da Figura 27a, Eivani et al. [43]
assumiram que o tarugo se move como um corpo rígido ao longo das regiões I e II, com
velocidade constante e igual a V0. Dessa forma, o material experimenta os elevados níveis
de deformação plástica, em condições de cisalhamento simples, ao atravessar a região II
(zona de deformação), limitada pelas superfícies de entrada (Γi) e saída (Γo), e cuja
extensão é definida pelo ângulo β. Ainda, admitiu-se que no interior da região II o tarugo
se desloca ao longo de trajetórias circulares concêntricas em O.
34
Figura 28: Modelo de deformação da técnica PCEA proposto por Eivani et al. [43].
A partir das hipóteses adotadas a expressão que define a pressão de prensagem (p)
foi obtida ao serem igualadas as taxas de trabalho externo realizado pelo punção sobre o
tarugo e o trabalho de deformação plástica do material que inclui as parcelas de atrito
oriundas do contato peça-ferramental, de cisalhamento atribuído na zona de deformação e
de corpo rígido observado antes e após as superfícies Γi e Γo. Assim,


Φ +β 
 H − L 
p = κ (1 + m ) 2 tg −1 
 + β + 4m 

 2  
 L 


(15)
onde H e L denotam a altura e a largura do tarugo, respectivamente.
Os efeitos de encruamento foram introduzidos no cálculo de κ a partir da tensão
média de escoamento (σm) corrigida pelo critério isotrópico de von Mises e associada à lei
de encruamento de Hollomon:
κ=
σy
3
= σm =
1
εb − εa
n
b
∫ [K ε ] dε
p
(16)
a
A solução analítica destinada à estimativa de ε proposta por Eivani et al. [43] foi
determinada pelo somatório entre as parcelas de cisalhamento imposto ao material durante
sua passagem pelas superfícies Γi e Γo e pela zona de deformação:
ε=

1
1 
−1  Φ + β 
( γ Γi + γ ZD + γ Γo ) =
 2 tg  2  + β
3
3

 
(17)
35
Estes autores comprovaram ainda a considerável dependência entre pressão e o
ângulo de interseção dos canais (Φ) e, em menor grau, com o raio de adoçamento externo
investigado em termos do ângulo β, como em Alkorta et al. [38] e Pérez [40]. Estes
comportamentos são apresentados na Figura 29 em função do fator de atrito m.
(a)
(b)
Figura 29: Relação entre pressão, atrito e geometria da matriz. (a) m = 0 e (b) m = 0,5.
Adaptado de Eivani et al. [43].
É importante notar que as previsões de pressão obtidas por Eivani et al. [43]
foram definidas a partir do parâmetro p’ que desconsidera as dimensões do tarugo, ou seja:
p' =
p

 
H−L 
−1  Φ + β 
− 4m 
 = (1 + m )  2 tg 
 + β 
κ
 L  
 2   

(18)
Segundo Eivani et al. [43], a sensibilidade da pressão em relação aos ângulos Φ e
β está diretamente ligada ao caráter geométrico da solução obtida para as previsões de
deformação plástica efetiva, definida pela Equação (17) e mostrado na Figura 30a.
Finalmente, a solução proposta para o cálculo de pressão foi validada em termos de força
de prensagem pela comparação aos resultados obtidos experimentalmente para a liga de
alumínio Al 6070 a partir de matrizes com geometrias distintas (Figura 30b). As previsões
baseadas no MLS forneceram resultados superiores aos experimentais, porém da mesma
ordem de grandeza. Além disso, verificou-se a queda da carga para valores de β diferentes
de zero.
36
(a)
(b)
Figura 30: (a) relação entre deformação plástica efetiva e geometria da matriz e
(b) comparação entre as previsões teóricas e experimentais de força de prensagem.
Adaptado de Eivani et al. [43].
Recentemente, apoiando-se nas idéias sugeridas por Altan et al. [41] acerca dos
efeitos da zona morta e da previsão do tamanho da zona de deformação em função das
condições de atrito, Eivani et al. [44] aproximaram ainda mais as previsões de carga para o
caso em que β = 0º. A Figura 31 apresenta a geometria empregada neste trabalho. Esta é
caracterizada pela ausência de adoçamento e a presença de uma zona morta estabelecida na
porção inferior da matriz (zona III).
Figura 31: Geometria da matriz ilustrando o aparecimento da zona morta (III) no modelo
do método do limite superior proposto por Eivani et al. [44].
37
A minimização da Equação (15) destinada à previsão de força de prensagem em
relação ao ângulo β fornece:
 1
∂P
Φ+Ψ
 H − L 
2
= 2 L κ 1 − (1 + m) cotg 
 + Ψ + 4m 
 = 0
∂Ψ
2
2


 L 

(19)
de onde é possível definir uma solução explícita para o ângulo Ψ em função das condições
de atrito e o ângulo de interseção dos canais:
 (1 − m ) 
Ψ = 2 tg 
−Φ
 (1 + m ) 
(20)
Uma vez que Ψ é sempre positivo, a condição crítica de atrito para a formação da
zona de deformação, ou ainda, o aparecimento da zona morta, é definida por:
2
m crit =
1 − cot g (Φ / 2)
1 + cot g 2 (Φ / 2)
(21)
Substituindo-se a Equação (20) na Equação (15), chega-se à solução corrigida
para previsão de força:

 (1 − m ) 
 H − L  
P = 2L2 κ  (1 − m 2 ) + 2 tg 

 − Φ + 4m 

 L  
 (1 = m ) 
(22)
Em relação às deformações plásticas efetivas, a dependência explícita com as
condições de atrito foi obtida substituindo-se a Equação (20) na Equação (15):
ε=
N 
−1  Φ  
 2 tg    se m ≤ m crit
3
 2 
N
ε=
3

2

 (1 − m ) 
(1 − m )
+ 2 tg 

(1 + m )
 (1 + m ) 
(1 + m ) 
 se m > m crit
2 
(23)
38
Eivani et al. [44] reportaram que o estabelecimento da zona morta diminui com o
aumento do ângulo de interseção dos canais, como apresentado na Figura 32a. Isto se
confirmou pela relação entre ε e m a partir de patamares maiores para valores de mais
elevados de Φ, conforme apresentado na Figura 32b. Ainda, Eivani et al. [44] obtiveram
uma maior aproximação das previsões de força em relação aos resultados teórico e
experimental determinados previamente, como mostra a Figura 33c. Entretanto, apesar dos
avanços relacionados aos trabalhos desenvolvidos por Eivani et al. [43-44], resultados
ainda mais realísticos seriam obtidos ao se investigar o acoplamento entre o critério de
escoamento e a tribologia durante o processamento de materiais via PCEA. Por outro lado,
as soluções analíticas propostas por estes autores não permitem avaliar os efeitos causados
por diferentes configurações de matrizes relacionadas, especificamente, à presença de raios
de adoçamento distintos na região de interseção dos canais.
(a)
(b)
(c)
Figura 32: (a) relação entre força e atrito crítico; (b) efeitos de Φ e das condições de
atrito sobre ε e (c) comparação entre os resultados teóricos e experimentais de força.
Adaptado de Eivani et al. [44].
39
Recentemente, Pérez et al. [45] desenvolveram soluções analíticas em três
dimensões, baseadas no método do limite superior, para a estimativa da carga necessária ao
processamento de tarugos com seção transversal quadrada após um único passe de
prensagem, a temperatura ambiente. Para tanto, consideraram todas as variações possíveis
na geometria da matriz, ou seja, alterações no ângulo de interseções dos canais em
conjunto com as condições de Rint < Rext ou Rint > Rext, conforme apresentado na Figura 33.
(a)
(b)
Figura 33: (a) matriz com Rint < Rext e (b) matriz com Rint > Rext.
Adaptado de Pérez et al. [45].
Segundo estes autores, ao serem adotadas origens locais para ambos os raios de
adoçamento, as componentes descontínuas associadas ao campo de velocidades
cinematicamente admissível são eliminadas, ou seja, o processamento do material passa a
ser influenciado apenas pela velocidade inicial de prensagem. Ao mesmo tempo, por
conservação de volume podem-se estabelecer as relações entre os comprimentos
instantâneos do tarugo HENTRADA e HSAÍDA e suas dimensões iniciais, sendo H a altura total
e L a largura. Dessa forma, para o caso em que Rint < Rext (Figura 33a):
(π − Φ)  R int + R ext 
Φ +β
H SAÍDA + H ENTRADA = H − L cotg 
−



2
2

 sen  Φ + β  

 2 
(24)
40
Por outro lado, quando Rint > Rext, como mostrado na Figura 33b a conservação de
volume fornece:
(π − Φ)  R int + R ext 
Φ −β 
H SAÍDA + H ENTRADA = H − L cotg 
−



2
 2  sen  Φ − β  

 2 
(25)
O ângulo β que delimita a região dos raios de adoçamento é calculado a partir de
relações trigonométricas sobre a Figura 33. Assim, quando Rint < Rext:
  R ext R int
  L − L
β = 2 arctg  
  R int R ext
1 +  L − L

 Φ
 tg  
 2

2Φ
 + tg  
2







(26)






(27)
Entretanto, para Rint > Rext:
  R int R ext
  L − L
β = 2 arctg  
  R int R ext
1 +  L − L
 
 Φ
 tg  
 2

2Φ
 + tg  
2

Por fim, após considerarem todas as superfícies de contato entre o tarugo e a
matriz, Pérez et al. [45] propuseram as expressões que permitem estimar a pressão
normalizada pelo limite de escoamento em tração uniaxial para materiais perfeitamente
plásticos. Quando Rint é menor que Rext e adotando-se o critério de von Mises:






R
R
p
1  (π − Φ)
H
1


int
ext 

=
+ m 2 + (π − Φ) 
+
 1 −


Φ
+
β
Φ
σy
L
L
L


 +β 
3 


sen 

 sen 



 2 
 2 




+ L 2 H 
 W  L 




 



(28)
onde W e m denotam a espessura do tarugo e o fator de atrito, respectivamente.
Em relação ao segundo caso geométrico da matriz, ou seja, quando Rint é maior
que Rext:






R
R
p
1  (π − Φ)
H
1


int
ext 

=
+ m 2 + (π − Φ) 
+
 1 −

Φ
−
β
Φ

σy
L
L
L


 +β 
3 


sen 


 sen 


 2 
 2 




+ L 2 H 
 W  L 




 



(29)
41
No que diz respeito aos resultados, primeiramente os autores compararam as
previsões analíticas de pressão normalizada àquelas calculadas numericamente por meio de
um modelo tridimensional discretizado por elementos finitos. Para este fim, consideraram
a prensagem a frio de um tarugo de seção quadrada de 10 mm de lado e 80 mm de altura
no interior de uma matriz composta por raios de adoçamento de 2 mm com canais
interceptados a 90°, após um único passe. Além disso, assumiram m = 0,125 ao longo das
interfaces de contato entre a peça e a ferramenta e adotaram um comportamento
perfeitamente plástico para o tarugo, com σy = 94,6 MPa.
A Figura 34 apresenta a comparação entre os resultados teórico e numérico de
pressão normalizada. De acordo com Pérez et al. [45], as previsões máximas de pressão se
mostraram relativamente próximas, sendo que o valor analítico foi cerca de 12% maior que
o resultado numérico em razão do caráter conservativo do método do limite superior.
Figura 34: Comparação entre as previsões analítica e teórica de pressão normalizada.
Adaptado de Pérez et al. [45].
Além da validação mostrada na Figura 34, Pérez et al. [45] investigaram a
influência dos parâmetros geométricos da matriz sobre as previsões de pressão
normalizada para a mesma condição de atrito (m = 0,125) considerada previamente. De
acordo com os autores, o fator de atrito é um parâmetro que não pode ser facilmente
controlado durante a prensagem e deve ser reduzido de forma a minimizar a carga
necessária à deformação da peça.
42
A Figura 35 mostra a dependência da pressão normalizada com os raios de
adoçamento e a altura total do tarugo, ambos normalizados pela largura dos canais (L).
Pérez et al. [45] verificaram o aumento de carga refletido pelo acréscimo da altura total do
tarugo, ao passo que a elevação do raio de adoçamento externo contribuiu para a
diminuição das previsões de pressão normalizada, conforme apresentado na Figura 35a.
Sendo assim, pela forma da superfície obtida, os autores observaram que não há qualquer
interação entre Rext e H.
O aumento do raio de adoçamento interno (Figura 35b), por sua vez, promoveu
conduziu à elevação da pressão normalizada assim como o acréscimo da altura total da
peça. Entretanto, pelo fato de que Rint e H são variáveis independentes, a forma da
superfície de resposta oriunda desta análise levou à observação, por parte dos autores, da
inexistência de interação também entre tais parâmetros.
(a)
(b)
Figura 35: (a) dependência da pressão normalizada com Rext / L e H / L e (b) relação
entre a pressão normalizada, Rint / L e H / L. Adaptado de Pérez et al. [45].
A Figura 36 apresenta a influência dos valores normalizados de raios de
adoçamento, do ângulo de interseção dos canais (Φ) e da altura total do tarugo normalizada
pela largura dos canais sobre as previsões analíticas de pressão normalizada. De uma forma
geral, os autores observaram os efeitos contrários sobre p / σy quando se eleva Rint ou Rext,
ao passo que o aumento de Φ conduziu ao decréscimo da pressão normalizada,
invariavelmente.
Em relação às variações da altura total do tarugo e o ângulo Φ, mostradas na
Figura 36c, os autores verificaram que a pressão normalizada aumentou para tarugos de
maior altura ou quando Φ se aproximou de 80°.
43
(a)
(b)
(c)
Figura 36: (a) dependência da pressão normalizada com Rext e Φ; (b) relação entre p / σy,
Rint e Φ e (c) relação entre p / σy, H e Φ. Adaptado de Pérez et al. [45].
A partir deste trabalho, Pérez et al. [45] desenvolveram expressões analíticas
capazes de fornecer previsões confiáveis de carga oriundas da prensagem a frio de
materiais com comportamento aproximado ao caso de plasticidade perfeita, após um único
passe de processamento. É importante destacar que as expressões propostas são válidas
somente quando os raios de adoçamento possuem origens distintas, o que reflete também
na ausência de componentes descontínuas de velocidade.
Os autores concluíram ainda que o aumento do raio de adoçamento interno pode
conduzir ao aumento da deformação imposta à peça, acompanhado por uma pequena
elevação da carga de prensagem.
44
- Soluções analíticas baseadas no método de linhas de deslizamento (MLD)
Segal [46] observou, experimentalmente, que tarugos de elevado comprimento ao
serem deformados via a técnica PCEA exibiram um fluxo plástico aproximadamente
constante e proveniente da ativação de um único sistema de deslizamento. Além disso, a
capacidade de encruamento do material diminuiu à medida que este foi submetido a
repetidos passes de prensagem. Nestas condições, Segal [46] enfatizou que considerar um
comportamento perfeitamente plástico para o material processado se constitui em uma
aproximação razoável e o método de linhas de deslizamento permite obter uma solução
completa para este método de deformação plástica severa com as vantagens de possibilitar
análises de tensões e deformações no interior de uma zona altamente deformada
plasticamente e identificar os planos e direções de cisalhamento atuantes.
Primeiramente,
Segal [46]
estabeleceu
uma
geometria
de
deformação
desconsiderando os efeitos de atrito nas interfaces entre a peça e o ferramental, como
mostrado na Figura 37. Assumiu-se que o tarugo se move no interior dos canais com
velocidade V e que a zona plástica é definida pela linha OA.
Figura 37: Geometria de deformação em ausência de atrito. Adaptado de Segal [46].
Como não existem forças atuantes sobre o tarugo após atravessar a linha OA, a
tensão σ atuante sobre OA e a pressão de prensagem p são dadas por:
σ = − κ cot g φ
(30)
p = 2 κ cot g φ
(31)
onde φ denota o semi-ângulo entre os canais da matriz.
45
Em seguida, o autor estabeleceu que se há atrito (representado por τ) entre o
tarugo e a matriz, o campo de linhas de deslizamento inclui a região central AOB, a zona
de metal rígido AO1B e a porção BOC caracterizada por um estado uniforme de tensões, de
acordo com a Figura 38a.
(a)
(b)
Figura 38: Campos de linhas de deslizamento. (a) atrito idêntico sobre as regiões de
contato e (b) condições distintas de atrito. Adaptado de Segal [46].
Levando-se em conta o atrito no interior dos canais com relação entre largura e
altura dada por H/L, a pressão exercida pelo punção é calculada por:
−1
p = 2 κ [cot g η + 2 (η − φ)] + τ [sen η (sen η + cos η)] + 2τ (H / L)
(32)
onde o ângulo Ψ é dado por:
Ψ = 2 ( η − φ)
(33)
O terceiro caso, ilustrado na Figura 38b, corresponde à condição em que distintos
níveis de atrito são experimentados pelo material durante o contato com a matriz.
Entretanto, para a situação de lubrificação ideal as previsões de pressão são maiores que as
fornecidas pela Equação (31) e se assemelha a uma solução proveniente do método do
limite superior aplicada a um sólido perfeitamente plástico.
Em relação às deformações atribuídas ao material durante o processo de
deformação, Segal [46] considerou as parcelas de cisalhamento simples oriundas das linhas
OA e OB e da região AOB apresentadas na Figura 38a.
46
Assim, o cisalhamento (γ) experimentado pelo material sobre as linhas OA e OB
será:
(34)
γ OA = γ OB = cot g η
e na região AOB:
(35)
γ AOB = Ψ
A Figura 39 apresenta os estágios de distorção experimentados pelo elemento
abcd durante a prensagem através dos canais da matriz representados pelas linhas 1 e 2.
Figura 39: Histórico de deformação do elemento material abcd. Adaptado de Segal [46].
Considerando as Equações (34) e (35), a distorção completa deste elemento é dada
por:
2
γ = 2 cot g η + Ψ / sen η
(36)
Com base nestas soluções analíticas propostas, Segal [46] observou o aumento de
deformações com os passes de prensagem embora a quantidade de cisalhamento imposta
ao material depende fortemente dos sistemas de deslizamento associados a cada uma das
rotas de processamento. Estas observações foram provenientes de verificações
experimentais da prensagem do alumínio puro, para a validação das soluções
desenvolvidas, a partir das rotas A, B e C em um máximo de oito passes em matrizes com
Φ = 90º e 120º.
47
Em relação aos modelos de previsão de textura, destacam-se os trabalhos
desenvolvidos por Beyerlein et al. [47] e Tóth et al. [48] voltados ao estabelecimento de
modelos analíticos que relacionam os níveis de deformação plástica atribuídos ao material
com as respectivas orientações preferenciais das microestruturas obtidas.
Beyerlein et al. [47] estudaram as deformações plásticas oriundas de um único
passe de prensagem em uma matriz com interseção de canais a 90º considerando três
situações distintas: cisalhamento simples ideal, desenvolvimento de uma zona plástica
central de deformação (Figura 40a) e ocorrência de uma zona plástica de deformação
bipartida, como mostrado na Figura 40b.
(a)
(b)
Figura 40: (a) zona de deformação central e (b) zona de deformação bipartida.
Adaptado de Beyerlein et al. [47].
Considerando o caso ideal de cisalhamento simples, cada uma das componentes
de deformação foi calculada da seguinte forma:
sen Φ cos Φ 0
Φ 
ε = cot g   cos Φ − sen Φ 0
2
 0
0
0
(37)
48
Para a condição de uma zona plástica central, Beyerlein et al. [47] definiram o
tensor de deformações infinitesimais como:
1 + sen 2α


2


(1 + ρ m ) tg α − sen 2α
ε= 

2


0


(1 + ρ m ) tg α − sen 2α
2
 1 + sen 2α 
−

2


0

0


π
0 ; ρ m = − 2α

2


0

(38)
Por fim, as deformações provenientes de uma zona plástica bipartida podem ser
aproximadas pela razão entre as velocidades tangencial e normal aos planos de
deslizamento (π-αB1’) e (π-αB2’) referentes às linhas de cisalhamento AC e BD,
respectivamente esquematizadas na Figura 40b. Assim:
γ' (α' ) = tg (α + α' ) − tg α'
(39)
Os resultados obtidos por Beyerlein et al. [47] para a zona plástica central
revelaram uma forte dependência entre as componentes de deformação e o ângulo α como
mostra a Equação (38). Os autores observaram que a evolução de textura se mostrou
bastante influenciada pelas variações de α para um material perfeitamente plástico de
estrutura cúbica de face centrada (CFC). Segundo estes autores, as texturas obtidas são
características de deformação por cisalhamento. Entretanto, o decréscimo de α promove
rotações sobre as texturas em sentido anti-horário, causando significativas alterações em
seus máximos valores.
Para a zona bipartida de deformações, Beyerlein et al. [47] utilizaram três texturas
iniciais distintas oriundas de processos de trefilação, laminação e randômica que foram
comparadas às obtidas após 2 passes de prensagem pela rota A nas regiões inferior e média
da zona plástica. Os autores reportaram que a textura referente à região inferior
permaneceu inalterada após cada passe. Por outro lado, entre as texturas iniciais, a
randômica exibiu níveis baixos de cisalhamento enquanto as demais mantiveram as
mesmas características, indicando a ocorrência de elevadas rotações e baixo grau de
cisalhamento.
49
Os autores concluíram que a representação da zona plástica por meio de uma
região bipartida se mostrou mais coerente uma vez que permitiu identificar as
características mais relevantes da técnica PCEA. Além disso, a região superior desta zona
plástica exerceu maior influência sobre a amostra, já que nesta porção as deformações
plásticas são atribuídas ao material de forma gradual e a textura foi um indicador direto das
condições do processo de deformação. Por fim, Beyerlein et al. [47] indicaram que os
modelos analíticos propostos podem ser estendidos para materiais policristalinos sem a
necessidade do uso de métodos auxiliares como elementos finitos.
Tóth et al. [48] propuseram um modelo analítico consistente utilizando linhas de
fluxo para a descrição da deformação de materiais processados via prensagem em canais
equiangulares em uma matriz com canais interceptados a 90º. Além disso, o modelo
desenvolvido permitiu a previsão teórica de texturas que foram comparadas àquelas
obtidas experimentalmente para o cobre puro após 3 passes de prensagem a partir da rota
A. Para efeitos de comparação e validade da solução proposta, os autores realizaram
comparações com os modelos viscoplástico de Taylor e plástico policristalino.
Os resultados experimentais de textura para o cobre puro mostraram que a
condição inicial se caracterizou pela presença de fibras resistentes paralelas ao eixo y.
Além disso, os autores observaram uma considerável mudança de textura para sucessivos
passes de prensagem. Em contrapartida, Tóth et al. [48] verificaram uma considerável
semelhança entre a textura obtida após um único passe de prensagem e a resultante de um
ensaio de torção com uma quantidade de deformação cisalhante (γ) da ordem de 2, a qual
também é observada após um passe de processamento via PCEA. Portanto, os autores
comprovaram que as texturas provenientes da técnica PCEA podem ser classificadas como
texturas de cisalhamento simples.
A partir destas comprovações experimentais, Tóth et al. [48] estabeleceram uma
função corrigida para o fluxo do material, ou seja, evitando a descontinuidade de
deformações presente nos modelos de Taylor e de plasticidade policristalina. A partir do
esquema apresentado na Figura 41, a função de fluxo é dada por:
z
z
χ = ( L − x ) + ( L − y) = ( L − x 0 )
z
(40)
onde x define as posições de entrada e saída da linha de fluxo e o parâmetro z representa as
suas possíveis formas.
50
Figura 41: Descrição do campo de fluxo por linhas de fluxo. Adaptado de Tóth et al. [48].
Ao comparar os resultados experimentais com as previsões teóricas textura
calculadas com os modelos de Taylor, de plasticidade policristalina e a Equação (34),
Tóth et al. [48] observaram que as previsões oriundas do modelo de Taylor se
aproximaram aos experimentos somente para o primeiro passe. Por outro lado, o modelo
de plasticidade policristalina, por ser apresentar formulação mais completa em termos de
parâmetros materiais, forneceu previsões melhores até o segundo passe. Finalmente, o
modelo proposto praticamente reproduziu os resultados experimentais para o segundo
passe e permitiu uma melhor aproximação para o terceiro ciclo de prensagem. Segundo os
autores, este modelo revelou um importante aspecto sobre a técnica PCEA: o processo de
refinamento microestrutural não promove significativas alterações na textura durante o
primeiro passe, porém após o segundo ciclo as mudanças de textura são significativas.
Assim como Beyerlein et al. [47], os autores concluíram que as previsões de
texturas cristalográficas se constituem em um forte indicador do modo com que as
deformações plásticas são atribuídas aos materiais deformados por meio da prensagem em
canais equiangulares. Além disso, reportaram que a introdução de parâmetros de
anisotropia plástica no modelo de fluxo apresentado pode conduzir a resultados mais
acurados de previsão de textura.
51
3.4.2.3 Modelos numéricos
A Figura 42 mostra um esquema de classificação referente às abordagens
disponíveis na literatura que empregam a simulação computacional no estudo do
comportamento de materiais metálicos após o processamento via a técnica PCEA,
sobretudo com base no método dos elementos finitos (MEF). Pode-se observar que, de
uma forma geral, tanto os trabalhos que utilizam modelos bidimensionais (2D)
aproximados à condição de deformação plana quanto os que adotam modelamentos
tridimensionais (3D) se destinam a investigar os efeitos causados por variações de
configuração da matriz, temperatura, taxa de deformação, tribologia e rotas de
processamento. Independentemente da estratégia empregada na proposição dos modelos
numéricos, o foco central de análise se resume à busca pelas condições ideais de
deformação, ou seja, a combinação ideal entre parâmetros que possibilitem, após N passes
de prensagem, o desenvolvimento de uma extensa zona homogênea de deformações
plásticas efetivas ao longo das porções médias do tarugo acompanhada por níveis de carga
mais baixos. Especialmente para o caso bidimensional, há ainda trabalhos em escala
mesoscópica que se destinam às previsões de deformação a partir de modelos cinéticos
baseados em densidades de discordâncias resolvidos pelo método dos elementos finitos.
Frente à classificação ilustrada na Figura 42, a revisão acerca dos trabalhos de
caráter numérico associados à técnica PCEA será dividida em modelos bidimensionais no
estado plano de deformação e aqueles que realizam modelamentos em três dimensões.
PCEA – classificação das pesquisas que envolvem a simulação computacional
Escala macroscópica
(modelos 2D e 3D)
Efeitos de geometria da
matriz, temperatura, taxa
de deformação, condições
de atrito e rotas
Escala mesoscópica
Modelos cinéticos
Previsões de deformação por
densidade de discordâncias
Condições ideais de
processamento para a
obtenção de uma zona
plástica uniforme
Figura 42: Classificação dos modelos numéricos aplicados ao estudo da técnica PCEA.
52
- Modelamento bidimensional
O precursor da utilização da simulação computacional, baseadas em modelos 2D
discretizados por elementos finitos, no estudo de materiais processados via a técnica PCEA
foi o trabalho desenvolvido por Prangnell et al. [49]. Este trabalho, apoiado nas então
recentes soluções analíticas propostas por Iwahashi et al. [37] para o cálculo das
deformações plásticas efetivas, buscou avaliar os efeitos do ângulo Φ e das condições de
atrito após um único passe de prensagem em temperatura ambiente. A heterogeneidade na
distribuição das deformações plásticas efetivas ao longo da superfície do tarugo deformado
foi igualmente investigada. O material utilizado foi a liga de alumínio Al - 0,15% Mn e aos
parâmetros Φ e µ foram atribuídos os valores de 90º e 100º e 0 e 0,25, respectivamente.
Prangnell et al. [49] observaram que a região de heterogeneidade de deformação
efetiva se estendeu somente nas zonas periféricas do tarugo, ou seja, nas porções em
contato com o ferramental. Ainda, concluíram que a distribuição das deformações plásticas
efetivas se tornou mais heterogênea para Φ = 90º e com o aumento do coeficiente de atrito.
Segundo estes autores, a existência de uma zona morta na região inferior de interseção dos
canais da matriz foi o fator responsável pelo aparecimento destas heterogeneidades. Cabe
ressaltar que a verificação experimental da zona morta foi realizada por Shan et al. [42],
anos mais tarde.
Kim et al. [50] também verificaram tal zona morta durante o processamento das
ligas de alumínio Al 1100 e Al 6061-T6, esta última caracterizada como um material quase
perfeitamente plástico pelo seu baixo expoente de encruamento. Neste trabalho foram
utilizados modelos numéricos 2D, nos quais o ângulo Φ assumiu o valor de 90º e o atrito
entre o tarugo e a matriz foi desprezado (µ = 0). Os autores observaram que o tamanho
desta zona morta, ou em outras palavras, da zona de deformação depende fortemente do
comportamento plástico do material e não apenas da geometria da matriz. De acordo com a
Figura 43 pode-se notar que a liga Al 6061-T6 exibiu uma menor curvatura em
comparação a liga Al 1100, o que foi explicado pela maior capacidade de encruamento
deste último material.
53
(a)
(b)
Figura 43: Distorções da malha previstas pelo MEF (a) material encruável (Al1100) e
(b) material quase perfeitamente plástico (Al6061-T6). Adaptado de Kim et al. [50].
Kim et al. [50] verificaram ainda que o baixo grau de encruamento apresentado
pela liga Al 6061-T6 revelou altos níveis de heterogeneidade na distribuição das
deformações plásticas efetivas ao longo de todo o tarugo. Por outro lado, a liga Al 1100
mostrou heterogeneidades somente nas regiões de interface de contato peça-ferramental,
enfatizando a importância da plasticidade sobre a qualidade final de materiais deformado
via PCEA. Estes comportamentos são apresentados na Figura 44.
Figura 44: Distribuição de deformações ao longo do tarugo. Adaptado de Kim et al. [50].
Buscando interpretar o comportamento do tarugo ao longo do seu processo de
deformação em termos de carga de prensagem, bem como avaliar os efeitos produzidos a
partir das rotas A e C, Kim [51] desenvolveu modelos numéricos em deformação plana nos
quais as rotações realizadas sobre o tarugo após cada passe foram atribuídas ao ferramental
em um total de dois passes. Esta metodologia descartou a necessidade de se retirar a
amostra entre sucessivos ciclos, de acordo com a Figura 45a.
54
Em relação à matriz, Kim [51] considerou uma configuração desprovida de raios
de adoçamento com a interseção dos canais a 90º. As propriedades mecânicas do cobre
puro no estado recozido foram obtidas a partir de uma curva tensão-deformação calculada
por meio do modelo desenvolvido por Estrin et al. [62].
(a)
(b)
Figura 45: (a) modelos para a análise de deformação plástica e (b) curvas de carga
versus deslocamento do punção obtidas durante a PCEA. Adaptado de Kim [51].
Kim [51] observou que as curvas de carga calculadas para cada uma das rotas
consideradas, vide Figura 45b, apresentaram comportamentos similares caracterizados pela
presença de dois estágios distintos. O estágio I corresponde ao primeiro passe de
prensagem e apresentou níveis de carga idênticos para as rotas A e C, já que o tarugo não
sofreu qualquer rotação. Entretanto, o estágio II forneceu previsões de carga três vezes
maiores que as oriundas do estágio I. O autor atribuiu a este fato o encruamento do
material e à deformação severa com caráter acentuado de heterogeneidade devido ao efeito
de contrapressão induzido ao tarugo pelas paredes dos canais de saída da matriz.
Kim [51] concluiu que a rota A foi responsável por atribuir o cisalhamento de
forma mais intensa ao material que a rota C, principalmente durante o estágio II. Isto pode
ser explicado uma vez que a rota C se caracteriza pela presença das deformações
redundantes, conforme observado por Segal [6].
Em parte, a solução para a limitação dos modelos numéricos quanto à presença de
raios de adoçamento na região de interseção dos canais da matriz foi proposta,
primeiramente, por Srinivasan et al. [52].
55
Utilizando um material hipotético com comportamento rígido-plástico, os autores
avaliaram os efeitos causados por variações do ângulo Φ (90º, 120º e 135º) e somente do
raio de adoçamento externo (0 a 1 mm com incrementos de 0,25 mm) sobre os níveis e a
distribuição de ε observados ao longo da superfície deformada do tarugo. Além disso, a
influência das rotas de processamento (A, BA, BC e C) sobre a quantidade de deformações
plásticas induzidas ao material deformado foi investigada a partir de um número máximo
de seis passes de extrusão. Os autores utilizaram o método dos elementos finitos aplicados
à condição de deformação plana, em ausência de atrito, e observaram que a magnitude das
deformações plásticas efetivas foi afetada por Φ e pelo raio de adoçamento externo, sendo
que este último parâmetro exerceu influência também sobre a distribuição de ε . Ainda,
verificaram que quanto maior o raio de adoçamento externo, menor a quantidade de
deformação atribuída ao material por passe de extrusão, como mostrado na Figura 46. Este
comportamento foi também observado por Suh et al. [53] para o alumínio puro.
(a)
(b)
(c)
Figura 46: Distribuição de deformações efetivas ao longo do tarugo. (a) Φ = 90º;
(b) Φ = 120º e (c) Φ = 135º. Adaptado de Srinivasan et al. [52].
56
Kim [54] a partir de uma matriz com os ângulos Φ e β iguais a 90º simulou por
meio de um modelo 2D a extrusão em canais equiangulares da liga de alumínio Al1100,
desconsiderando os efeitos tribológicos, e apresentou a curva força vs deslocamento do
punção obtida após um único passe de processamento. Segundo este autor, a curva
resultante deste método de deformação plástica severa revelou cinco estágios distintos, de
acordo com a Figura 47. O estágio 1 caracteriza a passagem da porção frontal da amostra
pela zona de deformação localizada na região de interseção dos canais, na qual elevados
níveis de deformação são impostos ao material. O estágio 2 define o dobramento do tarugo
em direção ao segundo canal que ocorre quando a sua porção frontal ultrapassa
completamente a zona de deformação, demonstrando um leve aumento de carga. O terceiro
estágio marca o contato efetivo entre a parte frontal do tarugo e a região superior do
segundo canal, o que justifica o comportamento não-linear revelado. O estágio 4 define o
contato total entre a parte frontal da amostra e o canal de saída da matriz, demonstrando
uma sensível queda de carga e o aparecimento de um platô na curva força vs deslocamento
do punção. Os autores sugerem que esta queda de carga está associada ao decréscimo de
volume deformável de material no interior do canal de entrada da matriz. Por último, o
estágio 5 é aquele em que a parte final do tarugo experimenta o cisalhamento simples ao
atravessar a zona de deformação, causando um pequeno aumento de carga.
Figura 47: Carga de extrusão versus deslocamento do punção durante a técnica PCEA.
Adaptado de Kim [54].
Baseando-se nos trabalhos até então desenvolvidos onde a importância de um ou
outro parâmetro foi investigada, Dumoulin et al. [55] avaliaram os efeitos simultâneos
causados pela geometria do ferramental, condições de atrito e propriedades mecânicas
iniciais do material a ser processado sobre a homogeneidade.
57
Novamente, modelos numéricos bidimensionais discretizados por elementos
finitos foram construídos para um único passe a temperatura ambiente, a partir das
variações dos parâmetros analisados listadas na Tabela 2. Deve-se frisar que o ângulo β é
definido apenas pelo raio de adoçamento externo.
Tabela 2 Parâmetros utilizados. Adaptado de Dumoulin et al. [55].
Nível
1
2
3
Φ (º)
90
110
140
β (º)
0
(π-Φ)/2
(π-Φ)
σy, K, n (MPa, MPa)
(100, 0, 0)
(100, 340, 0,45)
(100, 2000, 0,7)
m
0
0,1
0,3
Dumoulin et al. [55] observaram que o expoente de encruamento e as condições
de atrito se mostraram mais relevantes sobre a homogeneidade de deformações plásticas
efetivas. Por outro lado, aumentando-se Φ e β houve uma redução no valor médio de ε
embora se atingisse o valor máximo de homogeneidade de deformações para ângulos
intermediários. Estes aspectos são apresentados na Figura 48.
(a)
(b)
(c)
(d)
Figura 48: Efeitos de parâmetros sobre a homogeneidade de deformações e a curvatura
da amostra: (a) ângulo Φ; (b) ângulo β; (c) parâmetros materiais e (d) atrito.
Adaptado de Dumoulin et al. [55].
58
A influência térmica é investigada para materiais de elevada resistência mecânica,
como é o caso dos materiais à base de titânio (e suas ligas), alguns aços e as ligas de Mg.
Semiatin et al. [56] foram pioneiros no estudo de materiais com elevada resistência
mecânica, no que se refere à influência da taxa de deformação e da temperatura sobre as
previsões de deformação plástica efetiva. Além disso, verificaram possíveis falhas destes
materiais ao serem processados em temperatura ambiente por um único passe de
prensagem, variando-se a velocidade de conformação. Os materiais empregados neste
trabalho foram o titânio puro, a liga Ti-6Al-4V e o aço AISI 4340. As temperaturas
utilizadas variaram entre 25ºC e 325ºC e as velocidades de prensagem foram 0,025 mm/s,
0,25 mm/s e 25 mm/s que correspondem às taxas médias de ε iguais a 0,002 s-1, 0,2 s-1 e
2 s-1, respectivamente. A matriz utilizada tem configuração com Φ = 90º e β = 0º associada
à inexistência de raios de adoçamento. Primeiramente, os experimentos revelaram que as
amostras de Ti puro apresentaram falhas caracterizadas por segmentos ao longo do
comprimento que se agravaram com o aumento da velocidade de prensagem, como mostra
a Figura 49a. Por outro lado, o aço AISI 4340 apresentou falhas somente para à maior
velocidade considerada, vide Figura 49b.
(a)
(b)
Figura 49: (a) titânio puro deformado a 25ºC e (b) aço AISI 4340 deformado a 325ºC.
Adaptado de Semiatin et al. [56].
Além disso, Semiatin et al. [56] verificaram por meio de modelos numéricos 2D
que o resfriamento da matriz durante a conformação não-isotérmica à quente pode acentuar
a tendência à falha do material. Nesse sentido, os resultados numéricos evidenciaram a
natureza de segmentação caracterizada pelo cisalhamento e perda de calor através do
ferramental durante a prensagem, conforme apresentado na Figura 50.
59
(a)
(b)
Figura 50: (a) contornos de deformação plástica efetiva e (b) temperatura final para a
prensagem não-isotérmica a quente de Ti-6Al-4V com taxa de deformação de 2 s-1.
Adaptado de Semiatin et al. [56].
Em relação às ligas de magnésio, Figueiredo et al. [57] utilizaram a liga ZK60
(Mg - 5,5% Zn - 0,5% Zr) para desenvolver um procedimento que possibilitasse a
prensagem de materiais mais complexos sem a ocorrência de segmentação ou falhas
reportadas previamente por Semiatin et al. [56]. Para tanto, conduziram as simulações a
200ºC variando-se o ângulo Φ (90º, 110º e 135º) e a sensibilidade à taxa de deformação
(s = 0, 0,2 e 0,4), desconsiderando-se os efeitos do atrito na interface peça-ferramental.
Além disso, adotaram a rota BC em uma matriz com um raio de adoçamento externo
correspondente a β= 20. Estes autores empregaram um máximo de 8 passes para verificar
os efeitos da sensibilidade à taxa de deformação frente a elevados níveis de deformação.
Figueiredo et al. [57] observaram que para um valor fixo de Φ, por exemplo,
Φ = 90°, o aumento de s induziu elevados níveis de heterogeneidade ao longo do
comprimento do tarugo após oito passes de prensagem (Figura 51a), o que promoveu um
comportamento similar em termos da distribuição de ε ao longo desta mesma região,
conforme mostrado na Figura 51b. Estes autores reforçaram ainda que o incompleto
preenchimento do canal de saída da matriz, em virtude de elevada sensibilidade à taxa de
deformação é um forte indicativo de nucleação de trincas na superfície da amostra.
60
(a)
(b)
(c)
(d)
Figura 51: (a) preenchimento do canal de saída da matriz em função de s, comparado ao
resultado experimental; (b) distribuição local de deformação para diversos valores de s;
(c) distribuição da taxa de deformação para diferentes configurações de matriz e valores
de s e (d) distribuição de danos em função de Φ e s. Adaptado de Figueiredo et al. [57].
Por outro lado, variando-se o ângulo Φ e mantendo-se uma condição fixa para
s, Figueiredo et al. [57] notaram que a forma das respectivas zonas de deformação depende
fortemente destes parâmetros, ou seja, zonas de deformação mais amplas foram obtidas
para altos valores de s e se tornaram mais estreitas com o decréscimo desta variável, como
pode ser apreciado na Figura 51c. Estes autores avançaram ainda no que se refere ao
cálculo dos níveis e da distribuição dos danos macroscópicos causados pela prensagem de
materiais resistentes.
61
Para tanto, utilizaram um modelo de falha no qual a fratura do material ocorre
quanto o parâmetro CN atinge um valor crítico, associado ao trabalho plástico de
deformação por unidade de volume, ou seja:
ε
σu
dε
σ
0
CN = ∫
(41)
onde σu e σ denotam a máxima resistência à tração do material deformado e a tensão
efetiva definida por um dado critério de escoamento. Portanto, A Figura 51d evidencia que
s afeta não somente o nível de danos ao longo da superfície deformada do material, mas a
sua distribuição. Contudo, os autores verificaram que o aumento do ângulo Φ reduziu os
níveis globais de danos, fornecendo uma estratégia para o processamento de materiais
como a liga ZK 60.
Os efeitos causados pela distribuição da taxa de deformação sobre o tamanho e
a forma da zona de deformações plásticas foram estudados por Kim [58] e Kim et al. [59],
a partir da solução proposta por Iwahashi et al. [37] para o cálculo das deformações
plásticas efetivas que é descrita na Equação (4). A geometria de deformação considerada
por Kim [58] na é apresentada na Figura 52.
Figura 52: Ilustração esquemática da técnica PCEA. Adaptado de Kim [58].
Segundo Kim [58], o tempo médio de deformação (∆t) ao longo da linha GG’
pode ser definido como o tempo de permanência do tarugo no interior da zona principal de
deformação ABC delimitada pelo ângulo β. Portanto:
∆t =
1 Lβ
2 V
(42)
62
A Equação (42) mostra que o tempo médio depende diretamente da geometria
da matriz, ao passo que é inversamente proporcional à velocidade do punção. Em outras
palavras, tarugos de elevada largura permanecem por mais tempo sob deformação para
uma velocidade constante de prensagem. Por outro lado, aumentando-se a velocidade de
prensagem para uma geometria fixa da matriz o tempo de exposição da amostra à
deformação plástica diminui.
A partir da expressão para o cálculo de ∆t, Kim [58] estabeleceu uma solução
analítica para a estimativa da taxa de deformações plásticas efetivas corrigida pelo critério
de von Mises em condições de cisalhamento:
.
ε=
1 
 Φ +β
 Φ + β  V 2
2 cot g  2  + β cossec 2  L β
3




(43)
Pode-se notar que a Equação (43) se limita aos casos em que β > 0, já que um
valor infinito para a taxa de deformação é observado quando β é igual a zero. Ao mesmo
tempo, os efeitos de geometria do ferramental e velocidade do punção exercem efeitos
.
inversos sobre as previsões de ε .
Em busca de verificar a validade da solução propostas para o cálculo da taxa de
deformação, Kim [58] e Kim et al. [59] desenvolveram modelos em condições de
deformação plana baseados no método dos elementos finitos (MEF) assumindo Φ = 90º e
135º e β = 0º, 45º e 90º. Além disso, os efeitos de atrito foram desconsiderados e ao tarugo
foi atribuído um comportamento plástico perfeito de forma a evitar a influência dos efeitos
tribológicos e da plasticidade e permitir-lhe avaliar somente o comportamento e a
.
distribuição de ε associados a cada uma das configurações geométricas consideradas.
Ainda, o autor avaliou a influência exercida pelo tamanho dos elementos utilizados na
discretização do tarugo sobre a distribuição dos valores de taxa de deformação.
A Figura 53 compara as previsões e a distribuição da taxa de deformação na
região deformada do tarugo, mantendo-se Φ = 90º e β = 0º, a partir de uma discretização
grosseira composta por 500 elementos (Figura 53a) e após um considerável refinamento da
malha totalizando 4500 elementos, mostrado na Figura 53b. Kim [58] verificou que a
malha grosseira originou um espalhamento da zona de deformações caracterizado por
perturbações ao longo dos contornos de iso-valores, como pode ser observado nas linhas A
até F. Estas perturbações reduzem a acurácia e a qualidade dos resultados obtidos via MEF.
63
O refinamento da malha, além de praticamente eliminar as oscilações ao longo das
linhas de iso-valores, revelou um estreitamento da região sobre a qual as deformações
permanentes são impostas ao material e o acréscimo dos valores calculados para as
camadas B até F.
(a)
(b)
Figura 53: Distribuição de valores da taxa de deformação (s-1). (a) malha grosseira e
(b) malha refinada. Adaptado de Kim [58].
A Figura 54 compara o efeito do raio de adoçamento, utilizando a malha refinada,
sobre a distribuição e as previsões da taxa de deformação, mantendo-se o ângulo Φ
constante e igual a 90º. Segundo Kim [58], a presença de adoçamento promove uma
ampliação da região plástica, em comparação ao caso sem raios. Além disso, ao se elevar o
valor de β de 45º (Figura 54a) para 90º (Figura 54b), grande parte da zona plástica passa a
ser delimitada pelas linhas de contorno A que são caracterizadas por níveis menores de
deformação.
(a)
(b)
Figura 54: Influência do ângulo β sobre a distribuição da taxa de deformação (s-1).
(a) β = 45º e (b) β = 90º. Adaptado de Kim [58].
64
A influência exercida pelo ângulo Φ sobre a taxa de deformação pode ser
apreciada na Figura 55, assumindo o valor de 135º para este parâmetro. Em ausência de
adoçamento (β = 0º), como mostra a Figura 55a, Kim [58] observou que na interseção mais
externa entre os canais desenvolveu-se uma região de perda de contato entre o tarugo e a
matriz, a qual provocou um leve decréscimo sobre os níveis de deformação
experimentados pela amostra. Além disso, o dobramento do material associado a esta
região de descolamento conduziu a mudanças de forma na região de deformação,
especialmente ao longo da linha A. Em contrapartida, a introdução do adoçamento
referente a β = 45º sobre esta configuração de matriz eliminou o descolamento do tarugo
ao longo da região mais externa de interseção dos canais. Entretanto, estabeleceu-se uma
intensa região de perda de contato ao longo da porção superior do canal de saída da matriz,
cuja contribuição para a queda dos valores de deformação experimentados pelo material foi
mais efetiva sobre os contornos B até F.
(a)
(b)
Figura 55: Influência dos ângulos Φ e β sobre as previsões de taxa de deformação (s-1).
(a) β = 0º e (b) β = 45º. Adaptado de Kim [58].
Por último, Kim [58] verificou a validade da Equação (37) comparando as
previsões analíticas com os resultados numéricos, ambos obtidos para cada uma das
configurações geométricas adotadas para o ferramental, de acordo com a Figura 56. Dessa
forma, confirmou-se o decréscimo das previsões de taxa de deformação em virtude do
aumento dos ângulos Φ e β. O autor observou que embora o acréscimo de Φ contribui para
o decréscimo da taxa de deformação, a influência do adoçamento desempenhou um papel
primário no processamento do material, uma vez que este parâmetro conduziu ao aumento
da zona plástica e do tempo de exposição da amostra às deformações permanentes.
65
Figura 56: Ilustração esquemática da técnica PCEA. Adaptado de Kim [58].
Em escala mesoscópica, o foco central é a descrição do encruamento de materiais
cristalinos submetidos a elevados níveis de deformação plástica, a partir de modelos de
densidade de discordâncias. Neste sentido, Baik et al. [60] analisaram o comportamento
em deformação via PCEA do alumínio puro policristalino a partir do método dos
elementos finitos acoplado à versão tridimensional do modelo baseado em densidade de
discordâncias desenvolvido por Tóth et al. [61] que se constitui em uma extensão da
formulação bidimensional apresentada por Estrin et al. [62].
O modelo utilizado por Baik et al. [60] assume que a densidade de discordâncias é
introduzida como variáveis escalares internas do modelo cuja evolução promovida pela
deformação determina o comportamento global de encruamento do material. Esta hipótese
foi combinada às considerações de plasticidade cristalina, o que permitiu considerar
simultaneamente o endurecimento por deformação e a evolução da textura. Foi introduzido
o conceito de material bifásico no qual uma célula interior contendo densidade de
discordâncias relativamente pequena (ρc) e paredes celulares de largura w com elevadas
densidades de discordâncias (ρw). Portanto, a densidade total de discordâncias (ρt) é obtida
por meio de uma regra de mistura definida por:
ρ t = f ρ w + (1 − f ) ρ c
onde f denota a fração volumétrica das paredes celulares.
(44)
66
A evolução de f é aproximada pela seguinte função empírica:
r
.r
(45)
f = f ∞ + (f o − f ∞ ) exp ( − γ / γ )
.r
na qual fo representa o valor inicial de f, ao passo que f∞ e γ definem a sua saturação em
grandes deformações e a taxa de variação de f em relação à deformação cisalhante γr.
O tamanho médio da célula (d) se relaciona com a densidade total de discordância
(ρt) por:
(46)
d = k / ρt
onde k é uma constante de proporcionalidade.
As equações cinéticas permitem então relacionar as componentes de tensão e
deformação nas regiões internas (τ cr ) e das paredes da célula (τ rw ) :
.r
r
.
1/ m
τc = α G b ρc (γ c / γ o )
.r
r
.
τw = α G b ρw (γ w / γ o )
. r
. r
(47)
1/ m
.
onde γ c , γ w , γ o , G, b e m definem as taxas de deformação nas regiões internas e paredes
da célula, o módulo de cisalhamento, a taxa de deformação de referência, o vetor de
Burgers e o índice de sensibilidade à taxa de deformação, respectivamente.
O parâmetro α é uma constante cujo valor utilizado foi 0,25. O comportamento
global da estrutura bifásica foi determinado por uma quantidade escalar τr calculada por:
(48)
τ r = f τ rw + (1 − f ) τ cr
Na Equação (47) a evolução da densidade de discordâncias no interior e nas
paredes da célula é calculada por:
1
ρc = α*
3
.
.
ρw =
*
.
.


.
6γc
γ
*

γw −Β
− ko  . c
13
 bd (1 − f ) 
b
γ


 o
ρw
.
6 Β γ c (1 − f )
bdf
.
23
+
3 Β * γ c (1 − f ) ρ w
fb




−1 n
.
(49)
γ c ρc
.
γ
− ko  . w
γ
 o




−1 n
.
γ w ρw
(50)
67
Em relação ao interior da célula, o primeiro termo descreve a taxa de geração de
discordâncias oriundas de fontes de Frank-Read. O segundo termo representa a perda de
discordâncias no interior da célula, causada por seus deslocamentos em direção às paredes
celulares. Os parâmetros α* e Β* são constantes geométricas. O último termo define o
aniquilamento mútuo de discordâncias governado pelo escorregamento transversal dos
sistemas de deslizamento. O parâmetro ko é uma constante e n caracteriza a sensibilidade à
taxa de deformação do processo de aniquilamento, sendo inversamente proporcional à
temperatura absoluta e aumenta com a energia de falha de empilhamento.
No que se refere às paredes da célula, representadas pela Equação (50), a primeira
parcela à direita da igualdade representa o ganho de densidade de discordâncias que é
proporcional à perda destas no interior da célula. A segunda parcela expressa o aumento de
densidade de discordâncias devido à ativação das fontes de Frank-Read na interface, em
conseqüência da imigração das discordâncias oriundas da região interior. A terceira parcela
contabiliza o aniquilamento das discordâncias localizadas nas paredes celulares por meio
de mecanismos de escorregamento dos sistemas de deslizamento.
A condição que satisfaz a compatibilidade de deformação ao longo da interface
entre a região interior e as paredes da célula de discordâncias é a seguinte:
.r
. r
.r
γc = γ w = γ
(51)
Os experimentos realizados por Baik et al. [60] foram conduzidos à temperatura
ambiente e consistiram em deformar tarugos de Al puro por quatro passes (rota C) em uma
matriz com interseção dos canais a 90º composta por um raio de adoçamento externo cujo
ângulo de abertura (β) foi de 20º. Por outro lado, a simulação computacional igualmente
conduzida em condições isotérmicas, compreendeu a implantação do modelo de densidade
de discordância no programa de elementos finitos ABAQUS, conforme algoritmo
mostrado na Figura 57a. Em relação aos passes de prensagem, o histórico de deformações
e tensões efetivas e os parâmetros ρw, ρc e f obtidos em um passe anterior foram atribuídos
como condição inicial a um tarugo não deformado e este foi submetido a um ciclo de
prensagem subseqüente, conforme apresentado na Figura 57b.
68
(a)
(b)
Figura 57: (a) algoritmo para o a simulação computacional utilizando o modelo de
encruamento baseado em densidade de discordâncias e (b) diagrama esquemático
ilustrando o procedimento de atualização para a simulação de passes consecutivos de
prensagem. Adaptado de Baik et al. [60].
Em primeiro lugar, Baik et al. [60] obtiveram uma boa concordância obtida ao
serem comparadas às curvas de encruamento experimentais, obtidas por ensaios de tração
uniaxial e numérica. O comportamento observado revelou um rápido acréscimo de tensão
durante o primeiro passe, seguido por uma diminuição da taxa de deformação e um
pequeno encruamento durante o terceiro e quarto passes. Estes aspectos são apresentados
na Figura 58. Os pontos experimentais dispostos na Figura 58b se referem à calibração
realizada pelos autores sobre os valores experimentais destacados na Figura 58a,
assumindo um incremento de deformação plástica efetiva igual a 1,02 durante cada ciclo
de prensagem.
69
(a)
(b)
Figura 58: (a) curvas de encruamento após cada um dos 4 passes, em comparação com a
condição inicial e (b) curva tensão-deformação efetiva para Al-puro e valores
experimentais obtidos após 1-4 passes. Adaptado de Baik et al. [60].
Além da evolução do encruamento associada a passes subseqüentes de
prensagem, o modelo utilizado por Baik et al. [61] permitiu investigar as variações de
dimensões da célula de discordâncias causadas pela rota C. A partir das células
apresentadas nas Figuras 59a, 59b e 59c, os autores determinaram o tamanho médio (d)
utilizando a técnica de microscopia eletrônica de transmissão (MET). Dessa forma, quando
as previsões numéricas de d foram confrontadas com os experimentos, a concordância
revelada permitiu uma segunda validação das soluções analíticas, conforme mostrado na
Figura 60. O primeiro passe foi responsável por um rápido decréscimo de d e, por outro
lado, os demais passes exibiram uma queda menos acentuada deste parâmetro.
(a)
(b)
(c)
Figura 59: Células observadas por meio de microscopia eletrônica de transmissão após
(a) 1, (b) 2 e (c) 4 passes. Adaptado de Baik et al. [61].
70
Figura 60: Variações do tamanho médio da célula calculadas numericamente e
comparadas aos resultados experimentais. Adaptado de Baik et al. [60].
- Modelamento tridimensional
Os modelos tridimensionais desenvolvidos para o estudo do comportamento de
materiais deformados pela técnica PCEA apresentam objetivos similares aos aproximados
à condição de um estado plano de deformações, como sugerido previamente na Figura 42.
Assim, o foco central dos trabalhos reportados na literatura é a busca pelas condições
ideais de processamento, ou seja, geometria da ferramenta, rotas de processamento,
condições de atrito, temperatura e taxa de deformação que possibilitarão a obtenção de
materiais com elevadas propriedades mecânicas associadas ao estabelecimento de uma
região com distribuição homogênea de deformações plásticas efetivas que se estenderá ao
longo do comprimento do tarugo após um número máximo de ciclos de prensagem que é
característico de cada material utilizado. Como será visto no decorrer deste tópico, a
principal justificativa apresentada pelos autores para o modelamento 3D deste método de
deformação plástica severa, de acordo com as referências [63-66], se baseia no fato de que
este considera todas as componentes de tensão e deformação observadas em processos de
conformação mecânica (principais e cisalhantes), ao contrário dos modelos simplificados
ao caso particular de deformação plana.
No contexto das condições ideais de processamento, os trabalhos reportados nas
referências [63-66] podem ser divididos em duas classes distintas, a saber, os que adotam
materiais processados a frio e aqueles cujos materiais apresentam maior resistência
mecânica e, por essa razão, precisam ser deformados em temperaturas mais elevadas.
71
A primeira classe de pesquisas apresenta como destaque os trabalhos
publicados por Suo e colaboradores [63-64]. Suo et al. [63] evidenciaram os efeitos
causados por diferentes condições de atrito (0 ≤ µ ≤ 0,15 com incrementos de 0,05) sobre a
distribuição das deformações plásticas efetivas ao longo do comprimento de um tarugo
fabricado a partir de um material hipotético e deformado por um único passe no interior de
uma matriz com canais interceptados a 120° e composta por um raio de adoçamento
externo delimitado por β = 20°. Estes autores observaram que o aumento do coeficiente de
atrito estático (µ) conduziu ao acréscimo de ε , como pode ser visto na Figura 61, o que
seria satisfatório se não constatassem a elevação da heterogeneidade na sua distribuição ao
longo do comprimento do tarugo.
Figura 61: Distribuição de ε ao longo do eixo X. Adaptado de Suo et al. [63].
Em seguida, Suo et al. [64] analisaram os efeitos das rotas A, B e C sobre os
níveis e a distribuição das deformações plásticas efetivas. Para tanto, utilizaram a mesma
geometria e condições de atrito descritas por Suo et al. [63]. Em relação ao tarugo, foi
adotado o mesmo material hipotético anteriormente mencionado e a sua prensagem foi
conduzida a frio por um total de dois passes.
72
As rotações características a cada rota de processamento foram atribuídas à
ferramenta e os passes foram realizados de forma seqüencial, ou seja, não houve a retirada
da amostra entre os ciclos de deformação, conforme apresentado na Figura 62.
Figura 62: Modelos para a simulação continuada da prensagem em canais equiangulares.
Adaptado de Suo et al. [64].
Segundo Suo et al. [64], a rota A apresentou maior caráter heterogêneo para a
distribuição das deformações plásticas efetivas, visto que esta é mais severa em
comparação as demais rotas. A rota BC apresentou maior homogeneidade de deformações,
quando comparadas às rotas A e C, o que a indica como a mais favorável na obtenção de
materiais ultrafinos com microestrutura uniforme. A distribuição de ε associada a cada
uma das rotas é mostrada na Figura 63.
Figura 63: Distribuição das deformações plásticas efetivas ao longo do plano X para
µ = 0. Adaptado de Suo et al. [64].
73
Apesar da importante contribuição apresentada por Suo et al. [64] com relação
aos efeitos das rotas sobre a homogeneidade de ε , a metodologia desenvolvida para a
simulação dos passes de prensagem apoiada em um material hipotético com
comportamento rígido-plástico impossibilita a determinação dos níveis de encruamento
experimentados pelo tarugo após cada ciclo. Outra restrição deste modelamento se apóia
no fato de que as rotações foram atribuídas ao ferramental, ou seja, o retorno elástico do
material observado após a sua retirada da matriz foi desconsiderado. Por fim, os autores
indicaram a rota BC como a mais satisfatória com base somente na homogeneidade de
deformações plásticas efetivas, sem a preocupação com as previsões de carga associadas a
este esquema de processamento.
A segunda classe de pesquisas de modelos tridimensionais está associada com a
simulação da prensagem de materiais com elevada resistência mecânica. A título de
exemplo, os trabalhos de Son et al. [65] e Jiang et al. [66], ambos relacionados à obtenção
de materiais com baixos índices de falha e segmentação, Son et al. [65] sugeriram que a
segmentação verificada por Semiatin et al. [56] poderia ser evitada ao se aplicar uma
contra pressão sobre a região frontal do tarugo imediatamente após a sua passagem para o
segundo canal da matriz. Para tal, os autores propuseram três esquemas distintos para a
aplicação de contra pressão. De acordo com a Figura 64a, o escoamento do tarugo foi
controlado pelas forças de atrito, pela ação de um punção sobre a sua parte frontal ou pela
capacidade de deslocamentos atribuída ao canal de saída da matriz. Em todos os casos,
foram utilizadas geometrias da matriz com Φ = 90° e o ângulo β assumindo os valores de
0°, 20° e 45°. Em relação às condições de atrito, assumiram-se os valores de 0,05, 0,2 e 0,4
para o fator de atrito adotadas. Em contrapartida, as propriedades mecânicas do material
foram obtidas por meio de ensaios de compressão conduzidos em temperaturas entre
300°C e 600°C, como mostra a Figura 64b. Entretanto, a temperatura inicial de simulação
foi de 450°C. Os efeitos das rotas de processamento A e C foram também investigados a
partir de um máximo de quatro passes.
74
(a)
(b)
Figura 64: (a) esquemas de aplicação de contra pressão e (b) curvas de encruamento
obtidas para o Ti puro em diferentes temperaturas. Adaptado de Son et al. [65].
Son et al. [65] verificaram que os efeitos de contrapressão promovidos pelas
condições de atrito causaram barreiras ao escoamento plástico do material à medida que se
tornaram mais severas, conduzindo à deterioração da superfície superior do tarugo e
provocando concentrações localizadas de deformação plástica efetiva, o que acabou por
elevar o caráter de heterogeneidade, como mostra a Figura 65a. Estes autores observaram
que a contra pressão aplicada diretamente sobre a amostra, quando aumentada, causou a
elevação das deformações plásticas efetivas. Contudo, ao se aumentar a contrapressão, o
preenchimento da região de interseção dos canais da matriz se tornou mais pronunciado,
causando maior heterogeneidade na distribuição das deformações plásticas efetivas,
conforme apresentado na Figura 65b. Por outro lado, a contra pressão exercida sobre o
tarugo a partir do deslocamento a porção inferior da matriz, embora fornecesse previsões
menores de ε , promoveu uma distribuição mais homogênea ao longo do comprimento da
amostra (Figura 65c) quando comparada aos casos anteriores. Segundo Son et al. [65] o
deslocamento da matriz reduziu a ação das forças de atrito e acabou por facilitar o
escoamento plástico do material.
75
(a)
(b)
(c)
Figura 65: Distribuição das deformações plásticas efetivas para os modelos de contra
pressão propostos. (a) forças de atrito; (b) contra pressão imposta sobre a amostra e
(c) deslocamento da parte inferior da matriz. Os resultados estão ordenados para valores
de contra pressão iguais a 100, 200 e 300 MPa. Em todos os casos, m = 0,05 e β = 0°.
Adaptado de Son et al. [65].
Em relação aos efeitos das rotas A e C, Son et al. [65] verificaram que o modelo
no qual a contra pressão é aplicada diretamente sobre o tarugo, a superfície do mesmo foi
deteriorada como resultado dos múltiplos passes, principalmente quando a rota A é
empregada devido ao grau de severidade imposto em razão da ausência de rotações da
amostra após cada ciclo de prensagem. Assim, os autores reportaram que a rota C se
mostrou mais adequada ao processamento do titânio puro por fornecer menores distorções
da malha de elementos finitos utilizada, o que se refletiu em maiores níveis de
uniformidade na distribuição das deformações plásticas efetivas. Estes resultados são
mostrados na Figura 66.
O trabalho desenvolvido por Son et al. [65] se mostrou mais completo que
aqueles realizados por Suo e colaboradores [63-64] no que se refere aos parâmetros
investigados e ao material considerado. Entretanto, limitações podem ser observadas com
relação à falta de análises acerca das previsões de carga associadas a cada esquema de
atribuição de contra pressão e às rotas consideradas.
76
(a)
(b)
(c)
Figura 66: Distribuição das deformações plásticas efetivas para os modelos de contra
pressão propostos após 2, 3 e 4 passes. (a) forças de atrito, rota A; (b) forças de atrito,
rota C e (c) deslocamento da parte inferior da matriz com pressão de 300 MPa, rota A.
Em todos os casos, m = 0,05 e β = 0°. Adaptado de Son et al. [65].
Jiang et al. [66], com base nas idéias propostas por Suo et al. [63] de que a rota
BC apresenta maior grau de uniformidade de deformações avaliaram, numericamente, o
processamento a 400°C de tarugos fabricados a partir de Ti puro após 1 a 4 passes de
prensagem, em relação aos níveis e distribuição de ε , a ocorrência de falhas do material e
os níveis de carga associados aos ciclos de deformação. Para tanto, mantiveram fixas a
geometria da matriz (Φ e β iguais a 90°) e as condições de atrito (µ = 0,1).
Os autores observaram o aumento das deformações plásticas efetivas associado
aos passes de prensagem (Figura 67a) e atribuíram às heterogeneidades encontradas os
efeitos promovidos pela geometria da matriz adotada, a qual força movimentos de
dobramento do tarugo durante sua passagem pela região de interseção dos canais. Em
relação à ocorrência de falhas, Jiang et al. [66] utilizaram o mesmo critério adotado por
Suo et al. [63] e verificaram um aumento de possíveis danos após dois passes,
principalmente sobre a superfície mais externa da amostra, além de constatarem uma
distribuição homogênea deste comportamento ao longo da seção transversal, como mostra
a Figura 67b.
77
(a)
(b)
Figura 67: (a) deformações plásticas efetivas após 1, 2, 3 e 4 passes e (b) distribuição de
danos para 1 passe (esquerda) e dois passes (direita). Adaptado de Jiang et al. [66].
Em relação às previsões numéricas de carga de prensagem, Jiang et al. [66]
evidenciaram o aumento de carga associado a sucessivos passes, conforme apresentado na
Figura 68. No entanto, reportaram que estas curvas têm uma forma comum independente
do número de passes realizado sobre a amostra, caracterizada por dois estágios distintos. O
primeiro estágio caracteriza o contato do tarugo com a região de interseção dos canais,
causando um abrupto aumento de carga em razão do elevado grau de encruamento que
experimenta. O segundo estágio define o término da passagem do material por esta região,
atingindo um estado permanente ao longo do canal de saída da matriz. Este comportamento
promove níveis de carga oscilando em torno de um valor médio e decresce gradualmente.
(a)
(b)
Figura 68: Previsões de carga de prensagem. (a) após 1 passe; (b) após 2 passes.
Adaptado de Jiang et al. [66].
78
3.5 CONSIDERAÇÕES GERAIS ACERCA DA REVISÃO BIBLIOGRÁFICA
Após esta revisão acerca dos principais trabalhos voltados ao processamento de
materiais via a técnica de prensagem em canais equiangulares, alguns aspectos podem ser
destacados em relação a cada uma das abordagens descritas, ou seja, experimentais,
teóricas e numéricas:
- As pesquisas de caráter experimental podem ser caracterizadas como o primeiro passo ao
entendimento da forma com que cada material se comporta ao experimentar níveis
extremamente elevados de deformações permanentes durante cada ciclo de prensagem,
uma vez que nenhum tipo de consideração ou simplificação prévias são estabelecidas
durante o processamento de cada material. Assim, a influência de cada parâmetro
(geometria do ferramental, condições de atrito, temperatura, taxa de deformação e rotas)
sobre as propriedades finais do material deformado e os respectivos níveis de carga pode
ser investigada com a garantia de resultados realísticos. Entretanto, embora uma grande
diversidade de materiais tenha sido analisada, os estudos experimentais ainda se mostram
limitados a algumas configurações específicas para a matriz de prensagem e a somente
algumas investigações dos efeitos causados pelas condições de atrito e taxa de deformação,
o que restringe as possibilidades de análises;
- Os estudos teóricos por sua vez, principalmente os definidos em escala macroscópica, se
mostraram bastante avançados a partir dos trabalhos baseados no método do limite superior
(MLS) desenvolvidos por Altan et al. [41] e, recentemente, por Eivani et al. [43-44]. Estes
trabalhos possibilitaram prever, com maior confiabilidade, os níveis de carga e
deformações plásticas efetivas obtidos a frio após um único passe de prensagem, já que
consideram os efeitos tribológicos, de encruamento do material deformado e da geometria
do ferramental no cálculo das previsões de carga. No entanto, as soluções analíticas
propostas por estes autores são limitadas a somente dois arranjos distintos para a
ferramenta, ou seja, a inexistência de raios de adoçamento na região de interseção dos
canais ou a apenas a presença de um raio de adoçamento externo. Além disso, mesmo o
trabalho atual de Pérez et al. [45] no qual é considerada a influência da geometria da matriz
sobre as previsões de carga se restringe à utilização do critério de plasticidade isotrópico de
von Mises na descrição do comportamento plástico do material deformado, o que descarta
a possibilidade de distinção entre materiais e a verificação do acoplamento entre o critério
de escoamento e a tribologia, característico de processos de conformação mecânica.
79
Nesse sentido, fica clara a necessidade de uma solução analítica mais flexível em termos
de plasticidade que permita obter previsões de carga e deformações mais próximas às
fornecidas pelos testes experimentais, visando assim uma descrição analítica mais rigorosa
do comportamento dos materiais deformados via a técnica PCEA que permitirá também
investigar, de uma só vez, a relevância de cada um dos parâmetros de interesse associados
a este método sobre estas previsões;
- Em relação à simulação numérica 2D da prensagem de materiais em canais
equiangulares, os maiores avanços se observam nos trabalhos de Kim e co-autores
[50-51, 54, 58-59], voltados ao estudo dos efeitos das rotas de processamento e taxa de
deformação sobre os níveis de deformação plástica efetiva e carga de prensagem e na
contribuição desenvolvida por Dumoulin et al. [55], na qual os efeitos de diversos
parâmetros sobre a homogeneidade de deformações permanentes após um único passe de
prensagem,
em
temperatura
ambiente.
Além
disso,
Semiatin
et
al.
[56]
e
Figueiredo et al. [57] investigaram os efeitos da taxa de deformação e temperatura em
materiais de elevada resistência mecânica, com ênfase no aparecimento de falhas durante o
processo de deformação. Por outro lado, destacam-se os trabalhos indicados nas
referências [63-66] que utilizam modelamentos 3D para avaliar os efeitos das condições de
atrito, rotas de processamento, temperatura e taxa de deformação sobre as previsões de
carga e deformações permanentes. Contudo, assim como nos estudos analíticos acerca
deste método DPS, a simulação computacional foi aplicada às verificações de conjuntos
específicos de parâmetros e seus efeitos. Assim, a classificação dos mesmos em termos de
relevância se mostrou prejudicada.
80
4. MATERIAIS E MÉTODOS
Neste capítulo são apresentados os materiais e os métodos adotados no
desenvolvimento dos modelos analíticos e numéricos voltados ao estudo do processamento
de materiais via a técnica PCEA. Visando organizar o detalhamento destes procedimentos,
este capítulo foi dividido em duas seções: MATERIAIS e MÉTODOS.
A seção MATERIAIS mostra em detalhes os diversos materiais utilizados no que
se refere às suas origens e condições de ensaio para a obtenção das respectivas curvas de
encruamento. Além disso, são apresentados também os ajustes necessários a cada curva a
partir de leis de encruamento em função da análise a que se destina cada um dos materiais.
A seção MÉTODOS aborda a descrição detalhada dos experimentos e modelos
teóricos e numéricos desenvolvidos ao longo do presente trabalho, respectivamente. Com
relação aos modelos teóricos, primeiramente é realizada a apresentação formal associada
ao método do limite superior visto ser esta a formulação empregada na proposição das
soluções para os cálculos de carga de prensagem. Em seguida, é apresentada cada uma das
soluções, a partir do estabelecimento das hipóteses e condições específicas relacionadas às
soluções propostas. Esta classe de modelos incorpora ainda a descrição do método de
planejamento de experimentos fatorial 2k utilizado na avaliação qualitativa da influência
dos diversos parâmetros considerados sobre as soluções propostas. Ao final desta parte são
descritas as análises realizadas bem como os respectivos parâmetros utilizados. Em
seguida, a etapa de simulação computacional é detalhada em termos da metodologia
desenvolvida para a construção dos diversos modelos numéricos bidimensionais e
tridimensionais considerados em conjunto com a descrição das respectivas análises e as
estratégias empregadas para a obtenção dos resultados.
81
4.1 MATERIAIS
A Tabela 3 apresenta os diversos materiais utilizados bem como as respectivas
propriedades mecânicas obtidas após ajustes realizados sobre as curvas de encruamento
obtidas experimentalmente por meio de ensaios de tração ou compressão uniaxiais.
Cabe ressaltar que, exceto para o material modelo e a liga de alumínio Al 6061, as
expressões contidas na Tabela 3 foram determinadas em seus trabalhos de origem.
Tabela 3 Propriedades mecânicas referentes aos materiais utilizados no presente trabalho.
Material
Origem
Ensaio
Liga Al 6070
Eivani et al. [43-44]
CU
σ y =179,3 ( ε )
Material modelo
(Lei de Hollomon)
-
TU
σ y = 500 ( ε )
Material modelo
(Leis de Hollomon e Peirce)
-
TU
Ajustes
σ y = 500 ( ε )
0, 20
0, 09
0 , 26
0, 20
 ε. 
1 + 
 η 


 . 
 ε 
 . 
 ε0 
0 , 011
Liga Al 6061
Chen et al. [67]
TU
Aço LI
(Livre de Intersticiais)
Moreira et al. [68]
TU
σ y = 544, 96 (0,0048 + ε )
Liga Al 1100
Nagasekhar et al. [69]
TU
σ y =173,79 ( ε )
σ y = 381( ε )
0 , 05
0, 235
0 , 304
onde CU e TU definem as condições de compressão e tração uniaxiais, respectivamente.
Os modelos numéricos desenvolvidos (2D e 3D) foram validados, em termos de
força de prensagem, a partir dos resultados experimentais alcançados após a prensagem a
frio em um único passe de um tarugo fabricado a partir da liga de alumínio Al 1100.
Este material, cuja composição química se encontra listada na Tabela 4, foi fornecido pela
Novelis do Brasil Ltda. no estado recozido. Em seguida, foi submetido à usinagem de
forma a originar tarugos com dimensões iguais a 50 mm de altura e seção transversal
quadrada com 9,5 mm de lado.
Tabela 4 Composição química da liga de alumínio Al 1100 (% em peso).
Mn
Mg
Si
Pb
Fe
Ti
Cu
Sb
Al
0,0012
0,0018
0,04
0,001
0,14
0,005
0,0003
0,001
balanço
82
4.2 MÉTODOS
4.2.1 Experimento de prensagem a frio da liga Al 1100
A liga Al 1100 foi deformada por um único passe via o método da prensagem em
canais equiangulares em temperatura ambiente e com velocidade controlada da ordem de
1 mm/s. A Figura 69 mostra o aparato utilizado neste ensaio, o qual se encontra em
funcionamento no Laboratório de Ensaios Mecânicos da EEIMVR / UFF. Este aparato
consiste em uma máquina universal Wolpert com capacidade máxima de 200 KN de carga,
um punção e a matriz destinada ao processamento. A matriz, composta por dois blocos de
um aço tipo ferramenta previamente submetidos a tratamentos convencionais para o
aumento da resistência deste material, teve os canais introduzidos em um dos blocos por
fresagem de modo a perfazerem um ângulo de interseção igual a 90º e apresentarem seção
transversal quadrada com área de 100 mm2. Além disso, para tornar mais fácil o
escoamento plástico do material e reduzir o esforço aplicado pelo punção sobre o
ferramental, um raio de adoçamento igual a 5 mm foi introduzido na região externa de
interseção dos canais. Por último, a resistência induzida pelas forças de atrito à passagem
do tarugo através dos canais foi minimizada ao se aplicar sobre estes o lubrificante à base
de MoS2 sob a forma de spray.
(a)
(b)
Figura 69: (a) aparato utilizado nos testes experimentais de prensagem da liga Al 1100 e
(b) interior da matriz contendo um tarugo deformado ao longo do canal de saída.
83
4.2.2 Modelamento teórico
4.2.2.1 A formulação do método do limite superior
Segundo Avitzur [70], soluções exatas em processos que envolvem plasticidade
são difíceis de serem obtidas. Assim, uma alternativa plausível é restringir a solução à
energia necessária para a conformação do material em questão, de forma a limitar as
previsões teóricas entre valores mínimos e máximos, definidos pelos chamados princípios
extremos, como reportado por Kobayashi et al. [71].
De acordo com Kobayashi et al. [71], a definição dos princípios extremos
necessita, em primeiro lugar, do estabelecimento do princípio dos trabalhos virtuais (PTV).
Por este princípio, para um dado campo de tensões σij em equilíbrio no interior de um
corpo deformável com as forças Fi aplicadas externamente, a taxa de trabalho interno
realizado neste corpo é igual àquela realizada pelas forças externas para todos os campos
de velocidade contínuos vj e continuamente diferenciáveis, ou seja, os campos virtuais de
velocidade. Portanto, pode-se escrever:
∫σ
•
ij
ε ij dV = ∫ Fi v j dS
V
(52)
S
A Equação (52) apresenta o princípio dos trabalhos virtuais, onde vj denota
.
qualquer campo virtual de velocidade e εij representa a taxa de deformação derivável de vj.
Kobayashi et al. [71] apresentam a existência de dois destes princípios associados a um
estado consistente para materiais rígido-plásticos que suportam deformação plástica em
condições de tração prescrita sobre a superfície SF e velocidades prescritas sobre a
superfície Sv. Dessa forma, a solução para este problema consiste de um campo de tensões
em equilíbrio e um campo de velocidade associado. O campo de tensões satisfaz as
condições de escoamento plástico nas quais as deformações ocorrem sem violar o critério
de escoamento adotado, enquanto o campo de velocidade satisfaz as condições de
contorno.
84
- O primeiro princípio extremo
O princípio dos trabalhos virtuais relacionado ao princípio do máximo trabalho
plástico permite reescrever a Equação (52) da seguinte forma:
*
*
•
∫ (σij − σij ) εij dV = ∫ (Fi − Fi ) v i dS
V
(53)
S
onde σij e vi representam uma solução completa para o problema de deformação plásticas
de um material rígido-plástico sob condições de contorno prescritas. Além disso, σ*ij define
qualquer estado de tensões que satisfaz as condições prescritas de tração e velocidade
representadas pelas superfícies SF e Sv, respectivamente. Segundo o princípio do máximo
trabalho plástico, tem-se que:
*
∫ (F − F ) v
i
i
i
dS ≥ 0
(54)
S
*
Conseqüentemente, Fi = Fi sobre superfície SF e S = SF + Sv . Assim:
*
∫ Fi v i dS ≥
∫ Fi vi dS
Sv
Sv
(55)
A Equação (55) define o primeiro princípio extremo, estabelecendo um limite
inferior para a taxa de trabalho obtida a partir de um campo de tensões admissível.
- O segundo princípio extremo
Este princípio, igualmente detalhado por Kobayashi et al. [71], fundamenta-se na
*
existência de um campo de velocidade vi que satisfaça a condição de incompressibilidade
*
e as condições de contorno de velocidade sobre Sv, de modo que v i seja cinematicamente
admissível. Para estas condições, o princípio dos trabalhos virtuais fornece:
•*
*
*
∫ σij εij dV + ∫ τ ∆v dS = ∫ Fi v i dS
V
*
SD
(56)
S
onde τ define a componente cisalhante do tensor σij atuante na superfície de
*
descontinuidade de velocidades SD com a parcela de velocidade tangencial de
*
descontinuidade ∆v * no campo v i .
85
*
Considerando-se que v i é uma solução real, a componente de cisalhamento τ se
iguala ao limite de escoamento em cisalhamento (κ) do material e o princípio do máximo
trabalho plástico postula que:
*
κ ∆v ≥ τ ∆v
*
(57)
E:
* •*
•*
(58)
σ ij ε ij ≥ σ ij ε ij
Substituindo-se as Equações (57) e (58) em (56):
* •*
*
*
∫ σij εij dV + ∫ κ ∆v dS ≥ ∫ Fi v i dS
*
V
(59)
S
SD
Da mesma forma que para o primeiro princípio extremo, tem-se as contribuições
aditivas das superfícies com tração (SF) e velocidades (Sv) prescritas sobre a superfície em
deformação S, ou seja, S = SF + Sv. Além disso, sobre a superfície Sv existe a igualdade
*
v i = v i . Portanto:
* •*
*
*
∫ σij εij dV + ∫ κ ∆v dS − ∫ Fi v i dS ≥ ∫ Fi v i dS
*
V
S
SD
(60)
S
*
*
onde v i define o campo de velocidade cinematicamente admissível, εij denota o campo de
*
*
taxa de deformação derivável de v i , | ∆v i | representa a quantidade de velocidade de
*
descontinuidade ao longo da superfície de descontinuidade de velocidades SD e sobre o
*
campo de tensões σij que satisfaz o critério de escoamento adotado.
A Equação (60) define o método do limite superior a partir da contribuição dos
três termos matemáticos dispostos à esquerda da igualdade que comparados ao termo
localizado à direita, relacionado às previsões reais de carga, fornecem uma previsão de
carga superior. O primeiro termo representa a potência dissipada no interior da zona de
deformação, enquanto o segundo denota a energia desprendida ao longo da superfície de
*
descontinuidade de velocidades SD . O terceiro termo, por sua vez, se refere à potência
dissipada em virtude das condições de contorno prescritas sobre o sólido deformável.
86
4.2.2.2 Soluções para o cálculo da carga de prensagem
Recentemente, Pérez e Luri [45] utilizando a descrição formal do método do
limite superior apresentada na Equação (60) desenvolveram soluções analíticas que
permitem estimar a carga de prensagem resultante da deformação a frio de tarugos após um
único passe de processamento. Entretanto, apesar destas soluções contemplarem todas as
variações geométricas possíveis sobre o ferramental e as interfaces de contato entre o
tarugo e a matriz, o comportamento mecânico dos materiais utilizados foram aproximados
ao caso de ausência de encruamento, ou seja, sob as hipóteses de materiais perfeitamente
plásticos e independentes dos efeitos da taxa de deformação. Dessa forma, no presente
trabalho são propostas generalizações às soluções analíticas propostas por Pérez e Luri [45]
para possibilitar o cálculo da carga necessária à prensagem a frio, após um único passe, de
materiais com encruamento do tipo isotrópico e que sejam sensíveis ou não aos efeitos de
taxa de deformação. Além disso, a influência dos critérios de escoamento plástico sobre a
previsão de carga é investigada com base em descrições distintas do escoamento plástico
propostas por Drucker e von Mises.
As soluções propostas por Pérez e Luri [45] para o cálculo da carga de prensagem
foram estabelecidas a partir de geometrias de matriz cujos raios de adoçamento, interno
(Rint) e externo (Rext) apresentam centros locais de origem. Para tanto, os autores utilizaram
o conceito de linhas de fluxo de pontos materiais na descrição do comportamento do tarugo
durante o processo de deformação observado na região de interseção dos canais da matriz.
A Figura 70 mostra a matriz composta por raios de adoçamento distintos, na qual
Rint < Rext, em conjunto com a descrição esquemática da linha de fluxo de um ponto
material q. Pode-se notar que o raio de adoçamento externo, tem origem local em O’. O
ângulo Φ denota a interseção dos canais ao passo que o ângulo β delimita a abertura
promovida pela presença dos raios de adoçamento. O ângulo β, apesar de ter sua origem
em O, exibe uma abertura local igual a π - Φ quando a origem está sobre O’.
87
(a)
(b)
Figura 70: (a) linha de fluxo do ponto material q para matrizes com Rint < Rext e (b) vista
ampliada da região que compreende a linha de fluxo. Adaptado de Pérez e Luri [45].
A posição do ponto q considerando a origem sobre O, pode ser obtida de forma
vetorial aditiva em coordenadas cartesianas por:
{Oq}xyz = { OO'}xyz + { O' q}xyz
(61)
Além disso, a dependência do vetor (O’q) com os parâmetros r e ϕ mostrados na
Figura 70 é expressa por:
{O' q}xyz = [− r cos ϕ; − r sen ϕ; 0] xyz
(62)
onde r e ϕ denotam a direção radial e o ângulo entre o raio de adoçamento externo e o
segmento O' q .
O princípio fundamental para que se estabeleça uma solução analítica baseada no
método do limite superior diz respeito à obtenção de um campo de velocidades que seja
cinematicamente admissível ao processo de deformação em questão. Sendo assim,
substituindo-se a Equação (62) em (61) e adotando-se um referencial inercial (Ref), o vetor
velocidade do ponto material q é dado por:
 r dϕ senϕ 
 d (−OO' − r cos ϕ)
x


dt
 dt



 d

 d O' q 
 dϕ

dϕ
=
(
−
OO
'
−
r
sen
ϕ
)
=
−
r
cos
ϕ
[sen ϕ; − cos ϕ; 0]





 =r
y
dt
dt
dt
dt
Re f  xyz





0
0






 xyz 
xyz
(63)
88
Assim, a velocidade do ponto q cuja origem é o ponto O’ é descrita por:
{ V (q) }rφz = 0; r dϕ ; 0

dt
(64)

Pérez et al. [45] admitiram as hipóteses de velocidade constante e igual a V0 para
o punção durante a prensagem e, em relação ao ponto q, velocidade absoluta V (q) = V0.
Neste caso tem-se que:
dϕ V0
=
dt
r
(65)
Dessa forma, o campo de velocidades consistente com a Figura 70 é dado por:
Vr = 0; Vφ = r
V
dϕ
= r 0 = V0 ; Vz = 0
dt
r
(66)
A Equação (66) mostra que ao assumirem o valor constante e igual a V0 para as
velocidades do punção e do ponto material q, Pérez e Luri [45] acabaram por eliminar a
descontinuidade de velocidades associada à passagem do tarugo na região de interseção
dos canais da matriz, ou seja, na zona de deformações.
Segundo Pérez e Luri [45], um procedimento análogo pode ser realizado para a
determinação do campo de velocidades quando se deforma um tarugo por meio de matrizes
com Rint > Rext, cuja geometria e linha de fluxo são apresentadas na Figura 71.
(a)
(b)
Figura 71: (a) linha de fluxo do ponto material q para matrizes com Rint > Rext e (b) vista
ampliada da região que compreende a linha de fluxo. Adaptado de Pérez e Luri [45].
89
Analogamente, adotando-se um referencial inercial, as componentes de
velocidade associadas ao ponto material q apresentado na Figura 71 são dadas por:
 dϕ

 d (OO ' − r cos ϕ) 
r
sen ϕ 
x

dt
 dt



 d

 d O' q

dϕ
 dϕ

=
(
OO
'
−
r
sen
ϕ
)
=
−
r
cos
ϕ
[sen ϕ; − cos ϕ; 0]


 =r



y
dt
dt
dt
dt
Re f  xyz





0
0





 xyz 


xyz
(67)
Com base nas Equações (63) e (67) pode-se notar que o ponto material revela a
mesma velocidade para ambas as geometrias de matriz ilustradas nas Figuras 70 e 71. A
partir do campo de velocidades obtido, as componentes de taxa de deformação podem ser
determinadas aplicando-se as relações desenvolvidas por Avitzur [70]:
∂ Vr
=0
∂r
•
V 1 ∂ Vφ
ε φφ = r +
=0
r
r ∂φ
•
∂ Vz
ε zz =
=0
∂z
(69)
•
1  1 ∂ Vr ∂ Vφ Vφ 
1 V0
ε rφ = 
+
−
=−
2 r ∂φ
∂r
r 
2 r
(71)
•
(68)
ε rr =
(70)
A verificação da condição de incompressibilidade determina a consistência do
campo de velocidades obtido por Pérez e Luri [45] a partir das hipóteses de velocidade
constante. Assim, considerando as componentes principais de deformação em um estado
de cisalhamento puro:
•
•
•
•
ε kk = ε1 + ε 2 + ε 3 =
1 V0
1 V0
+0−
=0
2 r
2 r
(72)
Uma vez determinados o campo de velocidades e as componentes de taxa de
deformação infinitesimais associadas à prensagem a frio de materiais via a técnica PCEA,
Pérez e Luri [45] aproximaram a Equação (60), que define o método do limite superior, ao
caso de inexistência de forças externas de tração atuantes sobre o tarugo. Assim:
* •*
*
∫ σij εij dV + ∫ τ ∆v dS ≥ ∫ Fi v i dS
V
*
SD
S
(73)
90
O primeiro termo da Equação (73) envolve a integração volumétrica da porção do
tarugo que ocupa a região da matriz responsável por deformá-lo plasticamente, ou seja, a
interseção dos canais. A Figura 72 mostra os arranjos geométricos da matriz com destaque
para as respectivas regiões de interseção dos canais.
(a)
(b)
Figura 72: Relações para o volume diferencial do tarugo durante a prensagem.
(a) Rint < Rext e (b) Rint > Rext. Adaptado de Pérez e Luri [45].
Portanto, as diferenciais de volume que representam cada uma das configurações
do ferramental apresentadas na Figura 72 são calculadas por:
r
dϕ dx para R int < R ext
Φ + β
sen 
 2 
r
dV = w
dϕ dx para R int > R ext
Φ
 − β
sen 
 2 
dV = w
(74)
(75)
onde w denota a espessura do tarugo.
O ângulo β é obtido para cada arranjo geométrico da matriz a partir de relações
trigonométricas determinadas a partir da Figura 73, a saber:

(R ext − R int ) tg [Φ / 2]
β = 2 arctg 
2
 L + ( R int − R ext ) + L tg [Φ / 2]

 para R int < R ext

(76)

(R int − R ext ) tg [Φ / 2]
β = 2 arctg 
2
 L + (R int − R ext ) + L tg [Φ / 2]

 para R int > R ext

(77)
onde L define a largura dos canais da matriz.
91
(a)
(b)
Figura 73: Determinação do ângulo β. (a) Rint < Rext e (b) Rint > Rext.
Adaptado de Pérez e Luri [45].
A partir da Figura 74, Pérez e Luri [45] definiram dependência entre as direções
radial (r) e horizontal (x) para estabelecer a posição radial do ponto material q em função
da geometria da matriz, a saber:

Φ +β Φ 
r = R int + x 1 − cotg 
tg
 para R int < R ext
 2   2  

(78)

Φ −β  Φ 
r = R int + x 1 − cotg 
tg
 para R int > R ext
 2   2  

(79)
(a)
(b)
Figura 74: Relação entre as coordenadas r e x do ponto material q. (a) Rint < Rext e
(b) Rint > Rext. Adaptado de Pérez e Luri [45].
92
O trabalho de deformação plástica, definido a partir do escoamento plástico em
•
•
cisalhamento puro, resulta em σ ij ε ij = 2 κ ε rφ . Assim, o primeiro termo da Equação (73) é:
•
V0
dV =
r
V
κ V0 w
Φ + β
sen 
 2 
V0
dV =
r
V
κ V0 w
Φ −β
sen 
 2 
κ ∫ 2 ε rφ dV = κ ∫
V
•
κ ∫ 2 ε rφ dV = κ ∫
V
L π -Φ
∫ ∫ dϕ dx =
0 0
L π- Φ
∫ ∫ dϕ dx =
0 0
κ V0 L w ( π − Φ )
Φ + β
sen 
 2 
κ V0 L w (π − Φ )
Φ − β
sen 
 2 
para R int < R ext
para R int > R ext
(80)
(81)
onde κ denota o limite de escoamento em condições de cisalhamento puro.
De acordo com Wagoner e Chenot [90], o segundo termo da Equação (73) pode
ser corrigido ao se adotar a lei de atrito de Tresca em que τ = m κ. Assim:
∫ τ ∆v dS = ∫ m κ V
0
SD
dS = m κ V0 S D
(82)
SD
onde SD define a área de contato entre o tarugo e a matriz e m denota o fator de atrito.
Segundo Pérez e Luri [45] e de acordo com a Figura 75, faz-se necessário
considerar alguns parâmetros para o cálculo de SD, a saber, o comprimento Hext entre o
tarugo e a matriz, os respectivos contatos HRint e HRext entre o tarugo e os raios de
adoçamento e os comprimentos da peça na entrada (Hentrada) e na saída (Hsaída) da região de
interseção dos canais da matriz.
B
A
C
D
A
D
B
C
(a)
(b)
Figura 75: Parâmetros geométricos necessários à determinação de SD. (a) Rint < Rext e
(b) Rint > Rext. Adaptado de Pérez e Luri [45].
93
O comprimento Hext é dado por:
Φ + β
H ext = L cot g 
 2 
para R int > R ext
(83)
Φ − β
H ext = L cot g 
para R int < R ext
 2 
(84)
Ao mesmo tempo, os comprimentos HRint e HRext são determinados por:
H R int = (π − Φ) R int
(85)
H R ext = (π − Φ) R ext
(86)
A área de contato SD pode ser dividida em S1 e S2, como mostra a Figura 76.
Neste sentido, a área S1 é dada por:
[
S1 = w 2 H entrada + 2 H ext + 2 H saída + H R int + H R ext
]
Figura 76: Áreas de contato tarugo-matriz S1 e S2. Adaptado de Pérez e Luri [45].
(87)
94
Substituindo-se as Equações (83) a (86) em (87):
 


 Φ +β 
S1 = w 2  H entrada + Lcotg 
 + H saída  + [(π − Φ) (R int + R ext ]  para R int < R ext
 2 

 

(88)
 


 Φ −β 
S1 = w 2  H entrada + Lcotg 
 + H saída  + [(π − Φ) (R int + R ext ]  para R int > R ext
 2 

 

(89)
Por outro lado, a área S2 é dada por:
∫ dS + 2 L H
S2 = 2
entrada
+ 2 L H ext + 2 L H saída
int erseção
(90)
A diferencial de área dS é determinada a partir das Equações (74) e (75). Assim:
r
dϕ dx para R int < R ext
Φ + β
sen 
 2 
r
dS =
dϕ dx para R int > R ext
Φ − β
sen 
 2 
dS =
(91)
(92)
A partir das Equações (91) e (92), o primeiro termo da Equação (90) é dado por:
∫
L ( π−Φ )
dS =
int erseção
∫
int erseção
∫ ∫
0
0
L ( π −Φ )
dS =
∫ ∫
0
0
r
dϕ dx para R int < R ext
Φ + β
sen 
 2 
(93)
r
dϕ dx para R int > R ext
Φ −β
sen 
 2 
(94)
Substituindo-se as expressões para r descritas nas Equações (78) e (79) em (93) e
(94) e realizando-se as simplificações pertinentes tem-se:
 R int + R ext 


2

 para R < R
dS
=
L
(
π
−
Φ
)
int
ext
∫
Φ
+
β


int erseção
sen 
 2 
(95)
 R int + R ext 


2

 para R > R
dS
=
L
(
π
−
Φ
)
int
ext
∫
Φ
−
β


int erseção
sen 
 2 
(96)
95
A área total SD pode ser calculada a partir da soma entre S1 e S2, ou seja:


 Φ +β
S D = w 2 H entrada + 2 L cotg 
+ 2 H saída + (π − Φ) [R int + R ext ] +

 2 








R int + R ext 

 Φ +β

+ L 2 H entrada + 2 L cotg 
+ 2 H saída + (π − Φ)
 para R int < R ext

 Φ + β  
 2 

sen

 2  



(97)


 Φ −β 
S D = w 2 H entrada + 2 L cotg 
+ 2 H saída + (π − Φ) [R int + R ext ] +

2











R
+
R
Φ
−
β




int
ext  
+ L 2 H entrada + 2 L cotg 
+ 2 H saída + (π − Φ)
 para R int > R ext

 Φ − β  
 2 

 sen 

 2  


(98)
Aplicando-se a hipótese de incompressibilidade plástica sobre a Figura 75a
(Rint < Rext) pode-se estabelecer que:
L ( π−Φ )
L w H = Lw H entrada + L w H saída + L w H ext + ∫
0
∫ dV
(99)
0
onde H denota a altura total do tarugo.
Reescrevendo-se a Equação (99), tem-se que:
 Φ + β  (R int + R ext )(π − Φ)
H entrada + H saída = H − Lcotg 
−
Φ +β 
 2 
2 sen 
 2 
(100)
Em contrapartida, para a condição mostrada na Figura 75b em que Rint > Rext, a
Equação (99) fornece:
 Φ − β  (R int + R ext )(π − Φ)
H entrada + H saída = H − Lcotg 
−
Φ −β 
 2 
2 sen 
 2 
(101)
Finalmente, substituindo-se as Equações (97) e (98) em (82) e considerando-se as
Equações (80) e (81), Pérez e Luri [45] propuseram as soluções analíticas destinadas à
previsão da pressão normalizada pelo limite de escoamento em tração/compressão uniaxial
(σy) originada após um único passe de prensagem a frio para materiais perfeitamente
plásticos.
96
Portanto, para Rint < Rext:






R
+
R
2
H
p
κ  (π − Φ)
1


int
ext

=
+m
+ (π − Φ) 
 1 −

 L
σy σy 
L
 Φ +β 
 Φ+β 


sen 

 sen 



 2 
 2 




+ 2H
 W




 



(102)
Além disso, para a condição de Rint > Rext:




p
κ  (π − Φ)
2H
 R + R ext
=
+m
+ (π − Φ)  int

 L
σy σy 
L
 Φ −β 

sen 



 2 



1

 1 −
Φ
−β 



 sen 
 2 



+ 2H
 W




 



(103)
As previsões de carga de prensagem (P) fornecidas pelas Equações (102) e (103)
são determinadas pelo produto entre a pressão e a área de seção transversal do tarugo:
P=pw L
(104)
No presente trabalho, propõe-se a extensão das soluções analíticas propostas por
Pérez e Luri [45] a materiais com encruamento isotrópico que exibem ou não dependência
à taxa de deformação em temperatura ambiente. Em primeiro lugar, para materiais que não
têm sensibilidade à taxa de deformação e considerando-se a lei de encruamento de Swift, a
tensão média de escoamento (σm) é obtida por:
n +1
p n
p
K [(ε 0 + ε ) − (ε 0 )
1ε
σ y = σ m = ∫  K (ε 0 + ε )  dε =



ε0 
ε (n + 1)
n +1
]
(105)
onde ε0 denota o encruamento inicial do material.
Em relação aos materiais com sensibilidade à taxa de deformação, foram adotadas
duas leis de encruamento viscoplástico. A lei de Hollomon foi utilizada na análise fatorial
2k a partir das propriedades da liga Al 6061 (Tabela 3), ao passo que ora a lei de Hollomon
ora a combinação entre os modelos de Hollomon e Peirce, mostrada na referência [72],
foram empregadas na comparação com os resultados numéricos obtidos por meio do
programa comercial Ansys, considerando estes dois casos distintos de comportamento
plástico. Nestas análises utilizaram-se as propriedades mecânicas do material modelo
(vide Tabela 3). Pela lei de Hollomon, a tensão de escoamento é calculada por:
1
σy = σm =
ε
p

p n ε


K
(
)
ε
∫
t
 T
0 
ε



s
( n + s +1)

Kε
 dε p = s
ε t T ( n + s + 1)

onde s representa o expoente de sensibilidade à taxa de deformação.
(106)
97
O termo tT define o tempo total de prensagem gasto pelo tarugo ao atravessar as
superfícies de entrada (Γi em azul) e saída (Γo em vermelho) da região de deformação do
material delimitada pela interseção dos canais da matriz (vide Figura 75) e no interior desta
região zona de deformação. Para estimar tT assume-se que ao penetrar a superfície Γi e ao
deixar a superfície Γo o tarugo consome tempos iguais já que a largura L dos canais
permanece inalterada.
É importante destacar que embora a taxa de deformação plástica efetiva apresente
valores distintos durante a passagem do tarugo nas superfícies Γi e Γo e na região de
interseção dos canais, o seu cálculo foi considerado a partir do valor total da deformação
plástica efetiva. Além disso, a taxa de deformação plástica efetiva é calculada avante, ou
seja, após a determinação do tempo total de permanência do tarugo nas regiões
mencionadas. Portanto, tT é obtido pela soma entre as parcelas de tempo de residência
sobre Γi e Γo e no interior da região de deformação, ou seja:
t T = t Γi + t Γo + t ZD = 2 t Γo + t ZD
(107)
onde t Γi ; t Γo e t ZD denotam os tempos consumidos pelo tarugo ao atravessar as superfícies
Γi e Γo e a região de interseção dos canais (zona de deformação – ZD), respectivamente.
Ao longo das superfícies de entrada e saída da zona de deformação, o espaço
percorrido pelo tarugo corresponde aos segmentos AB e CD associados às superfícies
Φ +β 
quando
Γi e Γo. Por relações trigonométricas tem-se que AB = CD = L cossec 
 2 
Φ −β 
Rint < Rext ou AB = CD = L cossec 
no caso em que Rint >Rext.
 2 
Para Rint < Rext, tem-se que:
t Γe
t Γs
∫ dt = ∫ dt =
0
0
1
V0
AB
∫ dx → t
Γe
= t Γs =
0
L
Φ +β 
cos sec 
V0
 2 
(108)
L
Φ −β 
cos sec 
V0
 2 
(109)
Ou ainda para Rint > Rext:
t Γe
t Γs
∫ dt = ∫ dt =
0
0
1
V0
AB
∫ dx → t
0
Γe
= t Γs =
98
No interior da zona de deformação, o tempo de permanência do tarugo é expresso
a partir da Equação (65), com base na hipótese de ausência de descontinuidade de
velocidades adotada por Pérez e Luri [45], ou seja:
t ZD
∫0 dt = Vr0
(π −Φ)
∫ dϕ
(110)
0
onde tZD denota o tempo gasto pelo tarugo ao atravessar a região de interseção dos canais.
Considerando-se x = L para a direção radial r definida nas Equações (78) e (79),
quando Rint < Rext, tem-se que:

R

 Φ + β   Φ    
t ZD = L (π − Φ)  int + 1 −  cotg 
 tg     
V0 
 2   2    

 L
(111)
Por outro lado, quando Rint > Rext, o tempo tZD é dado por:

R

 Φ − β   Φ    
t ZD = L (π − Φ)  int + 1 −  cotg 
 tg     
V0 
 2   2    

 L
(112)
Portanto, reescrevendo-se a Equação (107) para cada um dos casos geométricos
da matriz, o tempo total de prensagem é estimado por:






R


Φ
+
β


  
2
tT = L 
+ (π − Φ)  int + 1 −  cotg 
 tg  Φ     para R int < R ext
V0 
Φ+β 
 2   2   

 L
sen 



2


(113)



R

 Φ − β   Φ    
2
tT = L 
+ (π − Φ)  int + 1 −  cotg 
 tg      para R int > R ext
V0 
L
2   2    
 Φ −β 



sen 



 2 
(114)
A validação das soluções para o cálculo do tempo total tT e, por conseguinte,
da taxa de deformação será feita por meio da simulação computacional utilizando o
módulo implícito do programa comercial ANSYS® versão 11.0. Esta metodologia será
apresentada posteriormente durante a descrição dos modelos numéricos desenvolvidos para
a simulação da prensagem via PCEA. Entretanto, no que se refere à determinação de σy,
este programa disponibiliza como lei de encruamento com maior facilidade de
convergência a relação de Peirce [72] estabelecida para a parcela de encruamento de
materiais com sensibilidade à taxa de deformação.
99
Definindo a tensão de escoamento a partir da tensão média e associando-se a lei
de Peirce à parcela estática definida por Hollomon tem-se:

n
1
σ y = σ m = ∫ K ε
ε 0

ε
 .
1 + ε 
 ι


s

 dε p = K

ε

 n
∫0  ε

ε

1 + ε
 tT
s


 dε p 


(115)
onde ι representa um parâmetro de viscosidade do material e foi considerado igual a 1.
A solução analítica da Equação (115) conduz a uma função hipergeométrica que
pode ser resolvida por expansão em séries de Taylor ou por técnicas de integração
numérica. Sendo assim, a última alternativa foi utilizada neste trabalho por meio da regra
do trapézio subdividindo-se o domínio delimitado pelos limites de integração em 100.000
vezes de forma a garantir maior acurácia nas previsões de tensão de escoamento.
- Influência do critério de escoamento sobre as previsões de p / σy
As Equações (102) e (103) mostram a relação κ / σy entre as tensões de
escoamento em cisalhamento simples e tração/compressão uniaxiais que influenciam
diretamente as previsões de pressão normalizada e os resultados de carga de prensagem. É
sabido que em função do critério de escoamento adotado para definir o comportamento
plástico do material deformado, a relação entre κ e σy apresenta correções distintas ao
serem relacionados os estados de tensão referentes ao cisalhamento e à tração/compressão
uniaxiais. Neste sentido, buscando avaliar a dependência das previsões de pressão (e carga)
com as superfícies de escoamento de forma a aproximar os resultados teóricos aos obtidos
experimentalmente, foram considerados no presente trabalho os critérios isotrópicos de
plasticidade de von Mises e Drucker [73] na estimativa da razão κ / σy.
Antes da apresentação formal destes critérios de plasticidade é necessário
estabelecer a condição em que ocorre a plasticidade, ou seja, aquela em que a forma da
superfície de escoamento é relacionada à lei de encruamento do material que define o seu
tamanho em função dos incrementos de deformação plástica efetiva impostos à amostra. A
condição de plasticidade é observada quando o incremento de deformação plástica efetiva
produz uma previsão de tensão de escoamento da mesma ordem que aquela proveniente do
critério de escoamento adotado. Quando ocorre esta igualdade, afirma-se que a tensão de
escoamento do material localiza-se exatamente sobre a região da superfície de escoamento.
100
O critério de plasticidade proposto por von Mises permite definir a função de
escoamento f (σij , ε) da seguinte forma:
f (σ ij , ε) = F (σ ij ) Mises − σ ( ε ) = 0
→
F (σ ij ) Mises = σ ( ε )
(116)
onde σ denota a grandeza efetiva de tensão identificada por uma medida de encruamento.
O tensor σij é definido em função das componentes hidrostáticas, responsáveis por
mudanças de volume, e desviadoras Sij que causam alterações de forma:
σ ij = σ m δ ij + S ij
(117)
onde σm = (1/3) σkk denota a tensão média e δij é o operador linear delta de Kronecker.
O tensor Sij, em particular, possui por três invariantes denominados J1, J2 e J3 que
podem ser definidos, para o estado de tensões principais, por:
J1 = Tr (Sij ) = S1 + S2 + S3
(118)
J 2 = 1 Sij Sij
2
(119)
J 3 = det (Sij ) =
1
Sij S jk S ki
3
(120)
O critério de von Mises é definido em função do invariante quadrático J2 por:
F (σ ij ) Mises =
3 J2 =
3 SS
2 ij ij
(121)
Portanto, em componentes principais, o critério de von Mises é dado por:
F (σ ij ) Mises =
[
3 S S = 1 (σ − σ ) 2 + (σ − σ ) 2 + (σ − σ ) 2
1
2
2
3
3
1
2 ij ij
2
]
1
2
(122)
101
Embora a técnica PCEA se caracterize pela deformação do material em condições
muito próximas ao cisalhamento simples, a relação entre κ e σy pode ser identificada ao se
comparar as soluções para F (σ ij ) Mises oriundas da tração/compressão uniaxiais e do
cisalhamento puro. Na verdade, em pequenas deformações, um estado de cisalhamento
simples pode ser obtido a partir de um estado de cisalhamento puro seguido de uma
rotação de corpo rígido.
Primeiramente, realizando-se a tração/compressão uniaxiais ao longo do eixo 1 de
tensões principais, a Equação (122) fornece:
F(σ ij ) Mises = σ y ∴ σ1 = σ y ; σ 2 = σ 3 = 0
(123)
Em seguida realizando-se o cisalhamento puro no plano 12 de tensões principais:
σ1 = − σ 2 = κ ∴ σ 3 = 0
(124)
Substituindo-se a Equação (124) em (122):
F (σ ij ) Mises = 3 κ
(125)
A partir da condição de escoamento plástico, a razão κ / σy associada ao critério
de von Mises aplicado ao cisalhamento puro será:
(κ / σ )
y Mises
= 1 / 3 ≅ 0,58
(126)
O critério de plasticidade proposto por Drucker [73], relacionado aos invariantes
J2 e J3 do tensor de componentes desviadoras Sij, é interpretado como uma correção do
critério de von Mises pela introdução de um parâmetro c que possibilita um achatamento
na superfície de escoamento entre os estados de tração/compressão planas e cisalhamento
puro, conforme mostrado na Figura 77. Estes fatos concordam com as previsões para
materiais isotrópicos CCC e CFC obtidas por Barlat [74].
1,25
1,25
1,00
1,00
0,75
0,75
0,50
0,50
Tresca
Drucker (c = 1,35)
von Mises
0,25
0,00
σ2 / σ
σ2 / σ
102
Tresca
Drucker (c = 2,025)
von Mises
0,25
0,00
-0,25
-0,25
-0,50
-0,50
-0,75
-0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 1,25
-0,75
-0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 1,25
σ1 / σ
σ1 / σ
(a)
(b)
Figura 77: Curvas de escoamento determinadas a partir dos critérios de escoamento de
Tresca, Drucker e von Mises. (a) metais CCC e (b) metais CFC.
A expressão desenvolvida por Drucker [73] é dada por:
[
F (J 2 , J 3 ) Drucker = (3 J 2 ) 1/2 1 − c (J 32 / J 32 )
]
1/6
[
= F (Sij ) Mises 1 − c (J 32 / J 32 )
]
1/6
(127)
No presente trabalho, assumiu-se c = 2,0 que corresponde a materiais cúbicos de
face centrada, como sugerido por Ferron et al. [75]. Deve-se notar que quando c = 0 o
critério de Drucker se reduz ao proposto por von Mises. Adotando-se um procedimento
análogo ao caso anterior, a tração uniaxial sobre o eixo 1 de tensões principais permite
obter:
J 2 = 1 / 3 σ 2y ∴ σ1 = σ y
(128)
J 3 = 2 / 27 σ 3y ∴ σ1 = σ y
(129)
Substituindo-se as Equações (128) e (129) em (127), o critério de Drucker
aplicado à tração/compressão uniaxiais terá como resultado:
F (J 2 , J 3 ) Drucker = σ y [1 − (4c / 27)]
1/ 6
(130)
103
Em contrapartida, pelo cisalhamento puro sobre o plano 12 de tensões principais:
J2 =
3 κ = F (σ ij ) Mises ∴ σ1 = − σ 2 = κ
(131)
J 3 = 0 ∴ σ1 = − σ 2 = κ
(132)
A substituição das Equações (131) e (132) em (127) resultará em:
(133)
F ( J 2 , J 3 ) Druc ker = κ 3
Substituindo-se a Equação (133) em (130) é possível estabelecer a razão κ / σy
pelo critério de Drucker:
( κ / σ y ) Druc ker = 1 / 3 [1 − (4 c / 27 )]
1/ 6
≅ 0,54
(134)
4.2.2.3 Soluções para o cálculo das deformações plásticas efetivas
Em relação às previsões de deformação plástica efetiva, são utilizadas neste
trabalho as soluções analíticas desenvolvidas por Pérez [40] e Luri [89] que contemplam as
combinações geométricas observáveis sobre o ferramental. Da mesma forma que no caso
da carga de prensagem, neste trabalho ambas as soluções são generalizadas em termos dos
critérios de plasticidade distintos estabelecidos por Drucker e von Mises.
O critério de escoamento adotado para definir o comportamento plástico do
material processado desempenha um papel primário sobre as previsões analíticas de
deformação plástica efetiva. Sendo assim, é necessário estabelecer as correções
provenientes dos critérios isotrópicos de plasticidade de von Mises e Drucker [73] sobre as
previsões de deformação plástica efetiva oriundas do processo de prensagem em canais
equiangulares, ou seja, em condições aproximadas para o cisalhamento puro.
•
Sob a hipótese de pequenas deformações, o tensor taxa de deformação ε ij pode
ser decomposto, de forma aditiva, em duas parcelas: a primeira diz respeito às
contribuições elásticas e a segunda está associada à parcela plástica. Assim:
•
•e
•p
•e
•p
ε ij = ε ij + ε ij
onde ε ij e ε ij denotam as taxas de deformações elásticas e plásticas, respectivamente.
(135)
104
Em métodos de deformação plástica severa como a PCEA é razoável considerar
que a contribuição da parcela elástica de deformação é infinitamente pequena frente aos
níveis de deformação permanente experimentados pelo material durante o seu
processamento. Neste sentido, a Equação (135) pode ser reescrita da seguinte forma:
•p
•
(136)
ε ij = ε ij
De acordo com Khan et al. [76], a lei associada ao escoamento plástico estabelece
•p
uma proporcionalidade entre o tensor ε ij e a superfície de escoamento a partir de uma
•p
função de potencial plástico f (σij). Esta proporcionalidade garante que qualquer vetor ε
seja normal à superfície de escoamento plástico. Portanto:
•p
•
•
ε ij = λ grad f (σ ij ) = λ
∂ f (σ ij )
∂ σ ij
(137)
•
onde λ é o escalar positivo chamado multiplicador plástico ou módulo de plasticidade.
O multiplicador plástico pode ser calculado empregando-se, primeiramente, a
identidade de Euler de funções homogêneas de grau n à função de escoamento plástico de
von Mises, ou seja, para a variável xi. Assim:
xi
∂ F (x i )
= n F (x i )
∂ xi
(138)
Como a função de von Mises é do tipo homogênea de primeiro grau em relação às
componentes de tensão, tem-se que:
σ ij
∂ F (σ ij )
= F (σ ij ) Mises
∂ σ ij
(139)
Em seguida, aplicando-se o princípio da equivalência do trabalho plástico
realizado por um estado qualquer de tensões com aquele decorrente das grandezas efetivas,
pode-se estabelecer, para materiais isotrópicos:
•p
•
σ ij ε ij = σ ε
(140)
105
Finalmente, substituindo-se a regra da normalidade definida na Equação (137) em
conjunto com a identidade de Euler apresentada em (139) na Equação (140), obtém-se:
•
•
(141)
λ =ε
A taxa de deformação plástica efetiva no sentido do critério de von Mises pode ser
obtida por meio da regra da normalidade definida na Equação (139), da seguinte maneira:
•p •p
•2
ε ij ε ij = ε
∂ f (σ ij , ε) ∂ f (σ ij , ε)
∂ σ ij
∂ σ ij
(142)
A derivada parcial localizada à direita da igualdade definida em (142) é dada por:
∂ f (σ ij , ε) ∂ F (σ ij ) ∂ F (σ ij )
=
=
∂ σ ij
∂ σ ij
∂ Sij
(143)
Ainda, pela Equação (122):
F (σ ij ) Mises = 3 Sij Sij
2
2
(144)
Portanto:
∂ F(σ ij ) 3
Sij
=
∂ Sij
2 F (σ ij ) Mises
(145)
Logo, a substituição de (144) e (145) em (143) fornece:
∂ F (σ ij ) ∂ F (σ ij ) 9
Sij Sij
=
= 3
2
∂ Sij
∂ Sij
4 F (σ ij ) Mises 2
(146)
Finalmente, substituindo-se (146) e (142), a taxa de deformação plástica efetiva
para o critério de von Mises para materiais isotrópicos é dada por:
•
ε=
2 •p •p
ε ij ε ij
3
(147)
106
A partir do segundo invariante do tensor de deformação plástica, para trajetórias
uniformes de deformação e em termos de componentes principais, o critério de von Mises
permite obter:
ε =
2
2
2
2 
( ε1 − ε 2 ) + ( ε 2 − ε 3 ) + ( ε 3 − ε1 ) 

3 
(148)
Aplicando-se o cisalhamento puro no plano 12, a Equação (148) fornece:
ε =
1
γ
3
→
ε1 = ε 2 =
1
γ ; ε3 = 0
2
(149)
onde γ / 2 denota a distorção angular por cisalhamento puro.
Por outro lado, na condição de cisalhamento puro no plano 12, o critério de
Drucker se reduz à descrição de von Mises, uma vez que neste estado J3 = 0. Em outras
palavras, em condições de cisalhamento puro ambos os critérios de escoamento apresentam
a mesma correção para a deformação plástica efetiva, ou seja:
ε Druc ker = ε Mises =
1
γ
3
(150)
A Figura 78 apresenta as configurações de matriz utilizadas por Pérez [40] e
Luri et al. [89] para o desenvolvimento das expressões para o cálculo das deformações
plásticas cisalhantes (γ) e, por conseguinte, das grandezas efetivas.
(a)
(b)
Figura 78: Geometrias de matriz para a determinação da deformação plástica cisalhante.
(a) Rint < Rext e (b) Rint > Rext. Adaptado de Luri et al. [89]
107
Segundo Pérez [40] e Luri et al. [89] o cálculo da deformação cisalhante
relacionado às geometrias mostradas na Figura 78 é similar e se baseia na distorção angular
responsável por transformar o elemento quadrado abcd no losango a’b’c’d’. Assim:
γ = a ' u = a ' t + tu
d' u
d' u
(151)
Ainda, por relações geométricas aplicadas sobre a Figura 78, pode-se escrever:
bc = ad = d ' u
(152)
as + sb' = dr + rc'
(153)
a ' t = rc'
(154)
 Φ +β
tu = as= adcotg 
para R 2 < R1
 2 
(155)
 Φ −β 
tu = as = ad cot g 
para R 2 > R1
 2 
(156)
onde R1 e R2 denotam os raios de adoçamento que delimitam a região de deformação
plástica para o elemento quadrado abcd, conforme mostrado na Figura 78.
Os segmentos sb’ e dr são obtidos a partir dos comprimentos dos arcos que
definem os raios R1 e R2, ou seja:
sb' = (π − Φ) R1
(157)
dr = (π − Φ) R 2
(158)
Portanto:
Φ +β
2 ad cot g 
+ (π − Φ) (R1 − R 2 )
2 

γ=
para R 2 < R1
ad
(159)
 Φ −β 
2 ad cot g 
+ (π − Φ) (R1 − R 2 )
2 

γ=
para R 2 > R1
ad
(160)
108
A relação entre os segmentos ad e as e os raios R1 e R2 é dada por:
ad + R 2 − R 1
Φ 
tg   =
as
2
(161)
A partir das Equações (156) e (161) tem-se:

 Φ + β   Φ 
R1 − R 2 = ad 1 − cot g 
 tg   para R 2 < R1
 2   2 

(162)

 Φ − β   Φ 
R1 − R 2 = ad 1 − cotg 
tg
 para R 2 > R1
 2   2 

(163)
A expressão para a deformação plástica cisalhante, quando R2 < R1 é obtida pela
substituição de (162) em (159), ou seja:

 Φ +β
 Φ + β   Φ 
γ = 2 cot g 
+ (π − Φ) 1− cot g 
tg


 2 
 2   2 

(164)
Ao passo que no caso de R2 > R1, a deformação plástica cisalhante é obtida
quando se introduz a Equação (163) em (160):

 Φ −β 
 Φ − β   Φ 
γ = 2 cot g 
+ (π − Φ) 1− cot g 
tg


 2 
 2   2 

(165)
Finalmente, reescrevendo-se a Equação (150) com base nas relações (164) e (165)
é possível obter as respectivas soluções para o cálculo da deformação plástica efetiva
associadas às matrizes ilustradas na Figura 78. Logo:
ε=

1 
Φ +β
 Φ + β   Φ 
+ (π − Φ) 1− cot g 
2 cot g 
 para R 2 < R1

 tg
3
 2 
 2   2 

(166)
ε=

1 
Φ −β
 Φ − β   Φ 
+ (π − Φ) 1− cot g 
2 cot g 
 para R 2 > R1

 tg
3
 2 
 2   2 

(167)
109
4.2.2.4 O método fatorial 2k para planejamento de experimentos
A metodologia descrita por Montgomery [77] para o planejamento fatorial 2k
estabelece que o efeito de cada parâmetro k sobre as variáveis de interesse é avaliado em
dois níveis, ou seja, cada parâmetro recebe valores mínimo e máximo. A partir das
combinações possíveis entre os parâmetros, o experimento ou as simulações são
reproduzidos para a obtenção da resposta individual de cada combinação de parâmetro
sobre as variáveis dependentes. Em seguida, com bases nos resultados de cada teste são
determinados os respectivos efeitos por meio da chamada matriz de planejamento e o
conjunto de efeitos é disposto em gráficos de probabilidades. Estes dados são ajustados por
regressão linear e os efeitos não coincidentes com a linha de regressão são relevantes sobre
a variável analisada. Por fim, realiza-se uma análise de variância sobre estes efeitos a fim
de se obter as superfícies de resposta para cada variável avaliada.
A metodologia apresentada por Montgomery [77] referente ao fatorial 2k aplicado
a uma única réplica de ensaios foi utilizada no presente trabalho. Foram avaliados os
efeitos da configuração da matriz (Rint, Rext e Φ), da superfície de escoamento plástico
(razão κ/σy) considerando-se os critérios de Drucker e von Mises, da tribologia
(fator de atrito m) e da taxa de deformação por meio da velocidade inicial de prensagem
(V0) sobre as previsões de pressão de prensagem e deformações plásticas efetivas
calculadas com os modelos propostos. Desta forma, se utilizou um total de seis parâmetros
avaliados a dois níveis, caracterizando um planejamento do tipo 26 cujas 64 combinações e
os parâmetros estão listados na Tabela 5.
De acordo com este planejamento, para a realização de uma análise de variância é
preciso determinar os efeitos associados a cada um dos parâmetros listados na Tabela 5 e
suas somas individuais e totais. Para tanto é necessário obter a matriz de planejamento 26
(Tabela 6) que relaciona as combinações utilizadas para as simulações, vide Tabela 5, os
efeitos principais (A até F) e, da mesma forma, as combinações.
110
Tabela 5 Combinações entre as variáveis consideradas no método fatorial 26.
Tabela 6 Matriz de planejamento para o método fatorial 26.
111
112
Uma vez determinada a matriz de planejamento, cada um dos efeitos e suas
combinações podem ser calculados da seguinte forma:
A, B, ..., ABCDEF =
2 soma (a , b,..., abcdef )
k
num 2
(168)
onde num define o número de réplicas realizadas sobre os experimentos.
A soma dos quadrados (SQ) de cada efeito sobre as variáveis de interesse é
definida por:
SQ A , B , ... , ABCDEF =
(SA , B , ..., ABCDEF )
2
(169)
num 2 k
onde SQA,B,...,ABCDEF representa a soma total de cada efeito após todas as combinações
mútuas. Além disso, a soma total dos quadrados (SQT) é dada pela diferença:
2
SQ TA , B , ..., ABCDEF
2
2 2 2
y ijl
= ∑ ∑ ∑ y ijl −
num 2 k
i =1 j=1 l =1
(170)
O primeiro termo da Equação (170) fornece a soma entre o quadrado de cada
resposta, pressão ou deformação, que é representada por y ijl 2 e está relacionada a cada uma
das combinações. O segundo termo representa o valor médio de cada resposta ao quadrado.
O erro (Er) associado à escolha dos parâmetros de relevância é dado pela
diferença entre a Equação (170) e a soma dos quadrados destes parâmetros, ou seja:
o
Er = SQ T A , B , ..., ABCDEF − ∑ SQ q
(171)
q =1
onde q considera desde o primeiro até o o-ésimo valor determinado pela Equação (170).
Por outro lado, para se realizar a análise de variância é necessária à determinação
do valor médio de Er, o qual é definido por:
Er =
E
GL q ,..., o
onde GL denota os graus de liberdade associados a cada efeito.
(172)
113
Por fim, podem-se efetuar os cálculos das variâncias (Fo) para cada efeito:
SQ q
Fo =
Er
(173)
As expressões para as superfícies de resposta associadas às previsões de pressão e
deformação plástica efetiva são determinadas por meio de modelos de regressão
multilinear. Os modelos utilizados neste trabalho têm a seguinte forma geral:
Π = ξ 0 + ξ A x A + ... + ξ ABCDEF x ABCDEF
(174)
onde Π pode ser a pressão (p) ou a deformação plástica equivalente ε , ξ0 define os
interceptos dos planos de cada superfície de resposta e ξA,…, ξABCDEF são os coeficientes
parciais de regressão. Além disso, xA,…,xABCDEF representam os efeitos principais e as suas
combinações e dependem dos valores máximos e mínimos adotados, ou seja:
{
= {R
[
− [( R
]} [
) / 2]}/ [( R
]
) / 2]
x A = R ext − (R ext min + R ext max ) / 2 / (R ext max − R ext min ) / 2
xB
int
int min
+ R int max
int max
− R int min
x C = { Φ − [(Φ min + Φ max ) / 2] }/ [(Φ max − Φ min ) / 2]
[
] [
x D = {( κ / σ y ) − ((κ / σ y ) min + ( κ / σ y ) max )) / 2 }/ ((κ / σ y ) max − ( κ / σ y ) min ) / 2
(175)
]
x E = { m − [(m min + m max ) / 2] }/ [(m max − m min ) / 2]
x F = { V0 − [(V0 min + V0 max ) / 2] }/ [(V0 max − V0 min ) / 2]
4.2.2.5 Análises teóricas realizadas no presente trabalho
As expressões analíticas propostas neste trabalho para os cálculos de carga e
deformações plásticas efetivas foram implementadas em linguagem Fortran90®. As
análises teóricas foram conduzidas sem consideração de efeitos de temperatura, ou seja, o
calor gerado pelo contato entre o tarugo e a matriz foi desprezado. Além disso, a influência
causada pelas rotas de processamento sobre os níveis de carga e deformações não foi
levada em conta, ou seja, os estudos teóricos executados se referem a um único passe de
prensagem.
114
O conjunto de análises teóricas realizadas divide-se, quanto aos objetivos centrais,
em três etapas.
A primeira etapa compreendeu a exploração das soluções propostas buscando
avaliar os efeitos causados pela geometria da matriz, condições de atrito e critérios de
plasticidade sobre as previsões de pressão de prensagem normalizada. Ao mesmo tempo,
em razão de seu caráter puramente geométrico e apresentar o mesmo fator de correção para
os critérios de plasticidade adotados, foram analisados somente os efeitos de parâmetros
geométricos do ferramental sobre as previsões de deformação plástica efetiva. Nestas
análises o material considerado foi a liga de alumínio Al 6070 cujos parâmetros plásticos
são apresentados na Tabela 3. Para tanto utilizou-se um tarugo de 50 mm de altura e seção
quadrada de 10 mm. Por outro lado, os valores adotados para os raios de adoçamento
produzem variações do ângulo β de abertura dos canais no intervalo 0º ≤ β ≤ 38º. Os
diversos parâmetros considerados neste conjunto de análises, bem como os respectivos
valores máximos e mínimos se encontram listados na Tabela 7.
Tabela 7 Parâmetros utilizados na exploração dos modelos analíticos propostos.
Parâmetros
Valor mínimo Valor máximo Incremento
90
135
15
Ângulo Φ (graus)
Raio de adoçamento interno, Rint (mm)
0
5,00
0,10
Raio de adoçamento externo, Rext (mm)
0
5,00
0,10
Fator de atrito, m
0,08
0,4
0,08
0,54 (Drucker) 0,58 (von Mises)
Razão κ / σy
A segunda etapa abrangeu a validação dos modelos propostos para materiais com
encruamento isotrópico e escoamento plástico definido segundo os critérios de von Mises e
Drucker. Para tanto, as respectivas previsões de carga de prensagem foram comparadas às
previsões experimentais máximas de força de prensagem obtidas após um único passe de
prensagem a frio da liga de alumínio Al 1100. Em concordância com as dimensões do
aparato descritas na seção 4.2.1 Experimento de prensagem a frio da liga Al 1100, foi
utilizado um tarugo com altura igual a 50 mm e seção quadrada de 9,8 mm. Além disso,
considerou-se a condição de lubrificação ideal atribuindo-se o valor de 0,08 ao fator de
atrito m.
115
A terceira etapa caracterizou-se pela classificação qualitativa da relevância de
parâmetros geométricos da matriz, tribológicos, razão κ / σy e da taxa de deformação sobre
as previsões de força por unidade de espessura e das deformações plásticas efetivas
(representada pela velocidade inicial V0). Além disso, foram determinadas as superfícies
de resposta associadas aos resultados encontrados. Assim, empregou-se o método fatorial
de planejamento de experimentos do tipo 26 apresentado anteriormente a partir dos
parâmetros listados na Tabela 8. O material utilizado nesta etapa foi a liga de alumínio
Al 6061 cuja curva de encruamento é apresentada na Tabela 3. Por fim, as dimensões do
tarugo foram 50 mm e seção quadrada de 10 mm.
Tabela 8 Parâmetros utilizados no método fatorial 26.
Parâmetros
Ângulo Φ (graus)
Raio de adoçamento externo, Rext (mm)
Raio de adoçamento interno, Rint (mm)
Fator de atrito, m
Razão κ/σy
Velocidade inicial, V0 (mm/s)
Valor mínimo Valor máximo
90
120
0
5,00
0
5,00
0,08
0,4
0,54
0,58
1
5
4.2.3 Modelamento numérico via o método dos elementos finitos
Nesta seção são descritos os modelos numéricos bidimensionais e tridimensionais
utilizados no presente trabalho em função do tipo de análise. O programa utilizado nas
simulações foi o código comercial baseado no método dos elementos finitos Ansys®,
versões acadêmicas 8.1 e 11.0. Cabe ressaltar que todas as simulações foram conduzidas
em temperatura ambiente, ou seja, desconsiderando-se o calor gerado ao longo das
interfaces de contato tarugo-matriz. Além disso, tais simulações foram realizadas de forma
quase-estática a partir da integração implícita no domínio do tempo. Em relação aos
modelos bidimensionais, o primeiro conjunto de análises diz respeito à verificação de
previsões de carga pela comparação aos resultados experimentais determinados por
Eivani et al. [43-44] após um único passe de prensagem para a liga Al6070 cuja curva de
encruamento é mostrada na Tabela 3. Buscando avaliar e explicar a forma das curvas
numéricas de carga obtidas a condição de plasticidade foi analisada para cada um dos casos
considerados a partir da comparação entre as curvas de encruamento e as fornecidas pelo
critério de von Mises para as grandezas efetivas de tensão e deformação.
116
Para garantir a imposição do nível de deformação plástica efetiva condizentes com
um único passe de prensagem, a curva de encruamento introduzida nos modelos numéricos
foi estendida a valores correspondentes a uma deformação plástica efetiva igual a 1,16.
Entretanto, para assegurar a coerência deste procedimento, estas mesmas análises foram
realizadas a partir da extrapolação da curva de encruamento até um valor máximo de
deformação plástica igual ao expoente de encruamento.
O segundo conjunto de simulações envolve a validação da formulação proposta
para o cálculo da taxa de deformação plástica efetiva observada após um único passe de
prensagem. Para tanto, foi utilizada a curva de encruamento apresentada na Tabela 3
referente ao material modelo. Devido à impossibilidade de serem criadas variáveis de
estado no módulo implícito do programa Ansys®, a validação destas soluções teóricas foi
realizada a partir das previsões numéricas de carga e deformações plásticas efetivas para os
casos de ausência de raios de adoçamento, apenas adoçamento externo e adoçamentos
interno e externo idênticos, os quais abrangem a formulação teórica proposta previamente
O terceiro conjunto de simulações se refere à determinação da condição crítica de
atrito, também após um único passe de prensagem, na qual não há aderência do material
prensado ao longo dos canais da matriz. O material utilizado foi o aço livre de intersticiais
(LI) a partir da curva de encruamento exibida na Tabela 3. Esta avaliação foi feita em
termos dos valores de pressão de contato e tensão tangencial de fricção em função de cada
valor considerado para o coeficiente de atrito estático de Coulomb (µ). Além disso, a
influência das condições de atrito sobre a homogeneidade na distribuição das deformações
plásticas efetivas foi verificada.
O quarto conjunto de análises numéricas mostra a comparação entre os resultados
de carga, tensão e deformações plásticas efetivas obtidos ora por modelos bidimensionais
ora por modelos em três dimensões para a liga Al 1100 (vide Tabela 3). O objetivo destas
simulações é validar e mostrar a consistência de modelos em deformação plana.
4.2.3.1 Previsões numéricas e experimentais de carga para a liga Al 6070
A Figura 79 apresenta as geometrias de matrizes destinadas à simulação
computacional para obtenção das previsões de carga de prensagem necessária à
deformação da liga de alumínio Al6070 após um único passe. Pode-se perceber que dois
casos distintos foram considerados, ou seja, no primeiro a matriz (Figura 79a) é
caracterizada pela ausência de raios de adoçamento na região de interseção dos canais ao
117
passo que no segundo (Figura 79b) foi introduzido somente um raio de adoçamento na
região externa de interseção. Estas configurações da matriz reproduzem os casos
considerados por Eivani et al [43-44] em seus testes experimentais de prensagem
conduzidos em temperatura ambiente para a liga de alumínio previamente mencionada.
Em relação ao caso de adoçamento externo, utilizou-se um raio de 16,16 mm
como mostrado na Figura 79b. Em todos os casos simulados o ângulo Φ de interseção dos
canais foi 90º. As matrizes foram consideradas como peças rígido-elásticas com
movimentos restritos em todas as direções e fabricadas a partir de um aço ferramenta H13
cujas propriedades mecânicas utilizadas foram o módulo de elasticidade E = 210 GPa e o
coeficiente de Poisson ν = 0,3. No que se refere às dimensões dos canais em ambas as
configurações a largura considerada foi 14 mm, como sugerido por Eivani et al [43-44].
Buscando avaliar os níveis máximos de deformações plásticas efetivas atribuídas
ao material os níveis de carga associados, em um primeiro momento as simulações foram
realizadas a partir da extrapolação da curva de encruamento até uma deformação efetiva
total de 1,16. Em seguida, apenas para a matriz desprovida de raios de adoçamento,
atribuiu-se um máximo de deformação plástica efetiva igual a 0,26 que corresponde ao
expoente de encruamento observado para a liga Al6070. Além disso, considerou-se o
critério de plasticidade isotrópico de von Mises para definir o comportamento plástico do
material durante a sua conformação. A geometria considerada é idêntica àquela utilizada
por Eivani et al [43-44] e foi comum às configurações de matriz mostradas na Figura 79.
Assim, utilizou-se um tarugo com 80 mm x 13,95 mm x 1 mm nestes modelamentos.
A pressão exercida pelo punção sobre a porção superior do tarugo foi representada
por incrementos compressivos de 0,25 mm de deslocamento ao longo do eixo Y até que
um total de 67 mm de altura do tarugo, inicialmente localizado no interior do canal de
entrada fosse transformado em comprimento no canal de saída da matriz.
118
(a)
(b)
Figura 79: Modelos para a simulação da prensagem da liga Al6070. (a) sem adoçamento
e (b) com adoçamento externo.
Na discretização das matrizes e dos tarugos foi empregado o elemento sólido
bidimensional PLANE 182 com formulação matemática aplicada à condição de
deformação plana e dotado de integração completa. Este elemento é composto por quatro
nós e apresenta três graus de liberdade, a saber, deslocamentos ao longo dos eixos
cartesianos X, Y e Z. A escolha deste elemento se apoiou no fato de que o mesmo é
indicado para o modelamento da conformação de sólidos incompressíveis, ou seja,
processos em que o corpo deformável não apresenta mudanças consideráveis de volume,
como é o caso da prensagem de tarugo através de canais equiangulares. Sendo assim, a
discretização do tarugo envolveu a utilização de 2.033 elementos finitos com 0,75 mm de
lado, sendo 19 utilizados ao longo da largura e 107 em sua altura. Em relação aos modelos
de matriz, se utilizaram elementos com 2 mm de comprimento.
Para as interfaces de atrito matriz-tarugo foi atribuído um contato do tipo flexível
cujas superfícies alvo para a matriz e contato para o tarugo. Os elementos utilizados foram
os chamados TARGE 169 e CONTA 171, compatíveis com o elemento PLANE 182. Com
base na severidade da técnica PCEA que acarreta elevadas pressões de contato ao longo
das interfaces peça-ferramenta, o algoritmo de contato utilizado se baseou no método de
Lagrange aumentado. Este método emprega séries iterativas de penalidades de forma que
as tensões de contato (pressão e atrito) são superestimadas durante as iterações de
equilíbrio. Sendo assim, a penetração final do tarugo sobre a ferramenta se torna menor
que a tolerância permitida que é ajustada automaticamente pelo programa Ansys® a cada
iteração, a partir de um valor inicial que depende da espessura dos elementos adjacentes à
interface de contato.
119
O modelo de atrito utilizado foi a rotina TAUMAX que se baseia na lei de
Coulomb. No domínio estático do atrito, esta lei estabelece uma proporcionalidade entre as
tensões cisalhantes e a tensão de escoamento em condições tração uniaxial. Portanto:
τ = µ σy
(176)
onde τ e µ denotam a tensão de cisalhamento e o coeficiente de atrito estático.
Aos modelos apresentados na Figura 79 assumiu-se µ = 0,104 sobre as interfaces
de contato, o que traduz o valor de 0,18 encontrado por Eivani et al [43-44] para o fator de
atrito m. Por outro lado, a tensão média de escoamento a 0,2% de deformação plástica
verdadeira foi 28,28 MPa. De acordo com a rotina TAUMAX, a máxima resistência ao
cisalhamento do material é observada na condição de aderência, ou seja, quando a tensão τ
é máxima e se iguala a κ. Assim:
τ MAX = κ = σ y / 3
(177)
Logo, o valor de τMAX informado à rotina TAUMAX para a liga Al6070 foi 16,33 MPa.
O método numérico utilizado nas simulações foi o de Newton-Raphson completo
associado ao método de convergência “line search” que introduz um parâmetro
multiplicativo aos incrementos de deslocamento em cada iteração numérica de forma a
melhorar a convergência do problema e evitar instabilidades sobre a solução. Este
parâmetro varia entre 0,05 e 1, sendo automaticamente determinado pela minimização da
energia potencial do sistema em solução.
O procedimento adotado para a obtenção dos resultados (pós-processamento)
dividiu-se em duas etapas, ou seja, a determinação das previsões de carga e da curva
tensão-deformação efetivas. A primeira fase consistiu no levantamento do valor total das
forças de reação presentes em cada um dos nós localizados no topo do tarugo,
considerando incrementos de 1 mm de deslocamento até 67mm. A segunda fase
correspondeu à obtenção da curvas tensão-deformação efetivas ora para o caso da matriz
desprovida de raios de adoçamento considerando as distintas extrapolações na curva de
encruamento ora para o modelo em que há adoçamento externo, no qual a máxima
deformação plástica efetiva foi de 1,16.
120
Para cada caso, isolaram-se blocos quadrados contendo 289 elementos
(destacados em verde na Figura 79) e determinaram-se os resultados no mesmo intervalo
usado para as cargas de prensagem. Em seguida, foram calculados os valores médios
destas variáveis entre os elementos para cada passo de deslocamento e as curvas
equivalentes obtidas foram comparadas às respectivas curvas de encruamento para o
mesmo nível de deformação plástica efetiva, com o intuito de se explicar o comportamento
do material em termos de carga a partir da verificação da condição de plasticidade em que
as tensões da curva de encruamento e do critério de plasticidade são idênticas.
4.2.3.2 Validação das soluções propostas para o cálculo da taxa de deformação
Uma etapa anterior à simulação computacional da prensagem de materiais com
sensibilidade à taxa de deformação via a técnica PCEA, sob a forma quase-estática, foi a
realização de testes simples para a verificação de como um valor constante de velocidade
de processamento pode ser introduzido ao longo dos passos de carga em termos de tempo e
deslocamento para então estabelecer uma metodologia de simulação. Sendo assim, foi
realizada a simulação de uma solicitação de tração uniaxial sobre um cubo com arestas de
10 mm, discretizado por um único elemento finito do tipo SOLID 185 com integração
reduzida. O elemento SOLID 185, dotado de oito nós, é o equivalente em três dimensões
ao elemento PLANE 182, ou seja, possui três graus de liberdade de deslocamentos em cada
nó e pode ser utilizado para a discretização de sólidos incompressíveis.
Ao cubo foi atribuído um comportamento elasto-plástico com encruamento
resultante da combinação entre as leis estática de Hollomon e dinâmica de Peirce
combinadas ao critério de von Mises. As propriedades mecânicas plásticas utilizadas se
referem ao material modelo mostrado na Tabela 3, as quais se aproximam de um aço do
tipo LI (Livre de Intersticiais). Para a parcela elástica assumiu-se E = 210 GPa e ν = 0,29.
O emprego de um material modelo ao tarugo se deve à extrema dificuldade em
serem obtidas junto à literatura associada à técnica PCEA curvas experimentais ou até
mesmo parâmetros plásticos ajustados à leis de encruamento para materiais processados a
frio.
121
Em relação à escolha do modelo para a descrição da parcela dinâmica de
encruamento, o programa Ansys® disponibiliza duas opções: as leis de Perzyna ou Peirce.
Entretanto, a lei de Peirce foi utilizada no presente trabalho com base nas investigações
realizadas por Perić et al. [72] que revelaram um maior grau de convergência quando se
adota tal solução em problemas que envolvem materiais sensíveis à taxa de deformação.
A Figura 80 apresenta a geometria do cubo considerado, discretizada por um
único elemento finito. As condições de contorno aplicadas para a correta simulação da
solicitação do cubo em condições de tração uniaxial foram as restrições de deslocamentos
sobre a área A1 ao longo do eixo Z, área A2 em X e da área A3 ao longo do eixo Y.
Figura 80: Cubo discretizado por um único elemento SOLID 185 com destaque para as
áreas com condições de contorno.
A dependência do material com a taxa de deformação foi simulada a partir de dois
valores distintos de velocidade, ou seja, 2 mm / s e 8 mm / s. Para tanto, foram estipuladas
curvas de velocidade em função do tempo para cada caso considerado de forma que a
partir um valor pré-determinado de deslocamento total, um pequeno valor inicial de tempo
(ti) fosse gasto até que se atingisse a velocidade desejada. Além disso, assumiu-se uma
proporção de cinco vezes entre os tempos final (tf) e inicial para a obtenção do critério de
parada da simulação e um deslocamento total de 4 mm aplicado sobre a área A4
(vide Figura 80). A Figura 81 apresenta estas curvas de velocidade utilizadas.
122
(a)
(b)
Figura 81: Curvas de velocidade para as simulações para deformação do cubo em tração
uniaxial com sensibilidade à taxa de deformação. (a) V = 2 mm/s e (b) V = 8mm/s.
A partir da relação entre os tempos inicial e final e observando-se que o
deslocamento total é a soma entre as áreas I e II mostradas na Figura 81, podem-se
determinar os valores de ti e tf para cada velocidade considerada e os respectivos
deslocamentos dI e dII. Estes serão os valores de tempo de deslocamento introduzidos em
cada modelo para representar o efeito da taxa de deformação como função da velocidade.
Portanto, quando a velocidade vale 2 mm / s:
t i = 2 t f − 4 = 2 (5 t i ) − 4 = 0,44 s
t f = 5 t i = 2,2 s
d I = t i = 0,44 mm
d II = 2 ( t f − t i ) = 8 t i = 3,52 mm
(178)
(179)
(180)
(181)
123
Por outro lado, quando V = 8 mm / s:
t i = 2 t f −1 = 2 (5 t i ) −1 = 0,11s
t f = 5 t i = 0,55 s
d I = 4 t i = 0,44 mm
d II = 8 ( t f − t i ) = 8 t i = 3,22 mm
(182)
(183)
(184)
(185)
O método de solução utilizado durante a simulação destes casos distintos foi a
versão completa de Newton-Raphson associado ao método de convergência “line search”.
Em termos de pós-processamento, foram obtidas e comparadas somente as
respectivas curvas tensão-deformação plásticas efetivas para cada passo de tempo até o
valor total de deslocamento, já que o programa Ansys® não permite a criação de variáveis
de estado em análises estáticas. Sendo assim, não foi possível determinar os valores e a
distribuição da taxa de deformação.
Após a realização dos testes para a realização de simulações que incluem os
efeitos de taxa de deformação, o procedimento foi adaptado à prensagem em canais
equiangulares. Neste conjunto de simulações, foram consideradas três configurações
distintas para a matriz, os quais englobam as soluções analíticas propostas para os cálculos
de carga e deformações plásticas efetivas. Dentre tais configurações, se observa o caso
geral que consiste na matriz desprovida de raios de adoçamentos e os casos particulares em
que ora a matriz exibe um raio de adoçamento externo ora os raios de adoçamento são
idênticos e diferentes de zero, conforme mostrado na Figura 82.
Em relação às dimensões das matrizes, utilizaram-se os mesmos valores adotados
para as análises previamente descritas, ou seja, canais com largura igual a 10 mm. Aos
raios de adoçamento interno (Rint) e externo (Rext) foi atribuído o valor de 5 mm e estes
foram construídos de acordo com as Figuras 82b e 82c, respectivamente. Em todos os
casos, o ângulo Φ de interseção dos canais foi mantido constante e igual a 90º.
124
Da mesma forma que na seção anterior, as matrizes foram consideradas como
peças rígido-elásticas com suas propriedades mecânicas referentes ao aço ferramenta H13,
ou seja, o módulo de elasticidade E = 210 GPa e o coeficiente de Poisson ν = 0,3.
As condições de contorno empregadas em todos os modelos de matriz foram o
bloqueio de movimentos nas direções X, Y e Z. Ao tarugo se atribuiu um comportamento
elasto-plástico com sensibilidade à taxa de deformação definido pela combinação entre as
leis de Hollomon para o encruamento estático e Peirce, descrito por Perić et al. [72], para a
parcela transiente. Ainda, as propriedades mecânicas plásticas utilizadas se referem a um
material modelo (Tabela 3) e a curva de encruamento foi extrapolada até 120% de ε . Em
termos de dimensões, foi utilizada para todos os modelos de matriz a geometria de
50 mm x 9,8 mm x 1 mm (altura x largura x espessura).
Da mesma forma que na seção anterior, para a discretização de matrizes e tarugos
se utilizou o elemento PLANE 182 com integração completa e aplicado ao estado plano de
deformações. Para as matrizes o comprimento de cada elemento foi igual a 2 mm. No caso
do tarugo considerou-se o comprimento de 0,75 mm, sendo necessários 14 elementos ao
longo do comprimento e 67 em sua altura, resultando em um total de 938 elementos.
A pressão exercida pelo punção sobre a porção superior do tarugo foi também
representada por incrementos compressivos de deslocamento ao longo do eixo Y.
Entretanto, para introduzir o efeito da taxa de deformação, os incrementos de deslocamento
foram associados a um valor proporcional de tempo de forma que após um tempo inicial de
2 segundos a velocidade de prensagem foi mantida constante e igual a 1mm / s. Este valor
corresponde à velocidade típica utilizada em simulações da prensagem de materiais
metálicos de forma dinâmica, como pode ser observado nas referências [50-51, 54].
Os deslocamentos totais considerados foram 40 mm para a matriz sem
adoçamentos (Figura 82a), 40 mm para raios idênticos e diferentes de zero (Figura 82c) e
45 mm para a configuração composta por somente o adoçamento externo (Figura 82b). Os
deslocamentos totais se referem à completa passagem do tarugo em direção aos canais de
saída de cada matriz. A curva-velocidade vs tempo utilizada é apresentada na Figura 83.
125
(a)
(b)
(c)
Figura 82: Matrizes destinadas à validação da solução para a taxa de deformação.
(a) sem adoçamentos; (b) com adoçamento externo e (c) raios de adoçamento iguais.
126
Figura 83: Curva velocidade vs tempo utilizada na simulação da prensagem em canais
equiangulares com efeito da taxa de deformação.
A partir da Figura 83 e com base no tempo inicial e nos valores totais de
deslocamento adotados para cada modelo é possível estimar os respectivos tempos finais e
deslocamentos dI e dII. Assim:
d T = d I + d II = 0,5 ( 2 t f − t i )
dI = ti / 2
d II = t f − t i
t f = 0,5 (2 d T + t i )
(186)
(187)
(188)
(189)
onde dT denota os valores totais de deslocamento considerados para cada modelo.
A Tabela 9 mostra os valores de tempo final e deslocamentos dI e dII em função da
configuração da matriz.
Tabela 9 Valores de tempos e deslocamentos em função do modelo de matriz.
Matriz
Adoçamento externo
Sem adoçamento
Adoçamentos idênticos
dI (mm)
1
1
1
dII (mm)
44
39
39
ti (s)
2
2
2
tf (s)
46
41
41
V (mm / s)
1
1
1
127
Analogamente à seção anterior, empregaram-se contatos flexíveis ao longo das
interfaces peça-ferramental com superfícies alvo para a matriz e contato para o tarugo. Para
a discretização das interfaces foram empregados os elementos TARGE 169 e CONTA 171.
Além disso, o algoritmo de contato adotado foi o método de Lagrange aumentado. O
modelo de atrito utilizado foi a rotina TAUMAX.
Aos modelos apresentados na Figura 82 assumiu-se uma condição de lubrificação
ideal com µ = 0,05. Por outro lado, a tensão de escoamento a 0,2% de deformação plástica
verdadeira foi 144,27 MPa. Ao mesmo tempo, obteve-se para TAUMAX o valor de
83,30 MPa a partir da Equação (177).
O método numérico utilizado nas simulações foi o de Newton-Raphson completo
associado ao método de convergência “line search”. O pós-processamento realizado após
cada simulação foi direcionado à obtenção das respectivas curvas de força na direção Y em
relação aos nós localizados sobre a porção superior do tarugo, em intervalos de 1mm de
deslocamento até o valor total considerado. Em seguida, a máxima previsão numérica de
força foi comparada aos resultados calculados com as soluções analíticas propostas com o
intuito de uma primeira validação.
As previsões numéricas de deformação plástica efetiva foram também utilizadas
para uma segunda validação dos modelos teóricos desenvolvidos. Para tanto, se utilizaram
os blocos quadrados destacados em verde na Figura 82 (144 elementos por bloco) e as
previsões deste parâmetro foram determinadas em intervalos de 1mm, com posterior
cálculo do valor médio representativo em cada passo de deslocamento. O máximo valor
médio fornecido por cada configuração de matriz foi então comparado às respectivas
previsões analíticas obtidas com a solução analítica proposta para o cálculo das
deformações plásticas efetivas.
A última etapa do pós-processamento consistiu na avaliação da distribuição das
componentes de deformação plástica ao longo da geometria deformada do tarugo
resultante do processamento por entre os canais de cada configuração de matriz. Os
objetivos centrais desta exploração são a verificação da influência da geometria da matriz
sobre a homogeneidade de deformações plásticas efetivas ao longo da superfície
deformada do tarugo e a análise do modo principal de deformação que governa cada
geometria de matriz.
128
Segundo Rosochowski et al. [78], é preciso manter uma determinada proporção
entre os raios de adoçamento para que o cisalhamento simples prevaleça como modo de
deformação predominante na região de deformação plástica do tarugo no interior da
matriz. Para esta finalidade, após o término de cada simulação a geometria deformada do
tarugo foi analisada ao longo das direções vertical e horizontal por meio do mapeamento
das componentes de deformação presentes em condições de estado plano de deformação.
Para os respectivos tarugos deformados foram escolhidos oito nós destinados aos
mapeamentos em cada direção de modo que as suas superfícies fossem divididas em quatro
partes, conforme apresentado na Figura 84. Os pontos destacados em preto e azula
representam os nós considerados ao mapeamento ao longo das direções vertical e
horizontal, respectivamente. Além disso, as respectivas setas em cinza escuro e verde oliva
mostram os sentidos adotados para tais análises. Dessa forma, as componentes cartesianas
(X,Y,Z e XY), principais (1ª, 2ª e 3ª) e efetiva das deformações plásticas foram
determinadas em função da distância entre cada um dos pares de nós.
(a)
(b)
(c)
Figura 84: Nós utilizados no mapeamento das componentes de deformação ao longo das
direções horizontal e vertical. (a) matriz com adoçamento externo; (b) matriz desprovida
de adoçamentos e (c) matriz composta por raios de adoçamento idênticos.
Por fim, para avaliar os efeitos de taxa de deformação, os modelos numéricos
apresentados na Figura 82 foram utilizados na simulação da prensagem do material modelo
cujo comportamento plástico exibe apenas a parcela relacionada à lei de Hollomon
(vide Tabela 3), ou seja, desconsiderou-se a contribuição da lei de Peirce que atribui ao
material a sensibilidade à taxa de deformação. As simulações foram igualmente conduzidas
em temperatura ambiente e à velocidade de 1 mm / s, conforme mostrado na Figura 83.
129
Dessa forma, os deslocamentos totais de cada tarugo foram de 40 mm para os casos sem
raios de adoçamento e na presença de raios de adoçamento iguais, ao passo que para a
matriz composta por somente o raio de adoçamento externo o deslocamento total foi de
45 mm. Em seguida, para efeitos de comparação às simulações com a inclusão da lei de
Peirce, foram determinadas as curvas de carga de prensagem em função do deslocamento
dos tarugos. Além disso, foram obtidas as previsões médias de deformação plástica efetiva
acompanhadas pela investigação dos modos principais de deformação associados a cada
configuração de matriz, de acordo com a Figura 84. Finalmente, buscando validar os
modelos analíticos propostos, as previsões máximas de carga de prensagem e deformação
plástica efetiva foram comparadas aos resultados analíticos considerando-se as leis de
Hollomon e a combinação Hollomon-Peirce e numéricas que incluem também este modelo
misto de encruamento.
4.2.3.3 Influência das condições de atrito
Estas análises têm por objetivos a investigação do aparecimento de aderência ao
longo das interfaces de contato matriz-tarugo e os efeitos promovidos por distintas
condições de atrito sobre a distribuição das deformações plásticas efetivas durante a
prensagem em canais equiangulares após um único passe de tarugos fabricados a partir de
um aço LI (Livre de Intersticiais). As matrizes foram consideradas peças elasto-rígidas
fabricadas a partir de um aço ferramenta H13 com E = 200 GPa e ν = 0,3. Duas
configurações de interseção dos canais foram utilizadas, ou seja, adotando-se os valores de
90º e 120º para o ângulo Φ, de acordo com a Figura 85. Em ambas as geometrias de
matriz, as condições de contorno empregadas foram restrições de movimentos em X, Y e
Z. Além disso, utilizaram-se canais com 10 mm de largura em conjunto com um raio de
adoçamento interno igual a 1,5 mm. Cabe observar que as soluções analíticas propostas
não consideram o caso em que o raio de adoçamento interno é maior que o externo. Por
esta razão, os resultados numéricos não puderam ser comparados às previsões teóricas de
carga e deformações plásticas efetivas.
130
(a)
(b)
Figura 85: Matrizes com diferentes ângulos de interseção dos canais utilizadas nas
simulações. (a) Φ = 90º e (b) Φ = 120º.
Em relação ao tarugo, atribuiu-se um comportamento elasto-plástico com
encruamento descrito pela lei de Swift associada às propriedades plásticas referentes a um
aço LI (Livre de Intersticiais) apresentadas na Tabela 3.
A extrapolação da curva de encruamento atingiu um máximo de 100% de
deformação plástica efetiva. Além disso, as propriedades elásticas adotadas foram
E = 200 GPa e ν = 0,3. Em todos os casos, as dimensões adotadas para o tarugo foram
50mm de altura, 9,8 mm de comprimento e espessura unitária.
O elemento PLANE 182 com integração completa e aplicado ao estado plano de
deformações foi utilizado para a discretização de matrizes e tarugos. Para as matrizes o
comprimento de cada elemento foi igual a 2 mm. No caso do tarugo considerou-se o
comprimento de 0,33 mm que resultou em um total de 4.590 elementos.
Os contatos aplicados às interfaces peça-ferramenta foram do tipo flexíveis com
superfícies alvo para a matriz e contato para o tarugo. A discretização das interfaces
envolveu a utilização dos elementos TARGE 169 e CONTA 171. O algoritmo de contato
adotado foi o método de Lagrange aumentado e o modelo de atrito utilizado foi a rotina
TAUMAX.
As condições de atrito consideradas nos modelos apresentados na Figura 85
compreenderam a ausência de atrito (µ = 0), uma condição de lubrificação ideal (µ = 0,05)
e situações mais severas assumindo-se os valores de 0,10 e 0,20 para o coeficiente de atrito
estático. A tensão de escoamento a 0,2% de deformação plástica verdadeira foi 155,80
MPa e forneceu para TAUMAX o valor de 89,95 MPa calculado com a Equação (177).
131
A pressão exercida pelo punção sobre a parte superior da amostra foi representada
por incrementos compressivos de 0,10 mm de deslocamento ao longo do eixo Y
(vide Figura 85) até que um total de 45 mm de altura do tarugo fosse convertido em
comprimento no interior do canal de saída da matriz.
A este conjunto de simulações o método numérico utilizado foi o de
Newton-Raphson completo associado ao método de convergência line search.
A obtenção dos resultados dividiu-se em três etapas de acordo com os objetivos
propostos para estas simulações numéricas. A primeira etapa teve como foco a análise da
ocorrência de aderência para cada condição de atrito atribuída ao longo das interfaces de
contato. Para tanto foram determinadas as curvas tensão cisalhante x pressão de contato
por meio do mapeamento dos valores de pressão de contato e tensões cisalhantes
experimentados pelos nós localizados nas extremidades do tarugo em função do tempo
adimensional de simulação contabilizado pelo programa Ansys®. Em contrapartida, foram
determinadas as curvas deslocamentos nodais em função do tempo computacional para a
confirmação do surgimento de aderência. Este mapeamento nodal seguiu o esquema
mostrado na Figura 86 no qual o lado esquerdo compreende a respectiva altura e a base do
tarugo. Ainda, entende-se por lado direito somente a referente altura da peça.
(a)
(b)
Figura 86: (a) desenho esquemático dos lados do tarugo usados na determinação das
curvas de atrito e (b) nós utilizados no mapeamento dos deslocamentos, pressão de
contato e tensão cisalhante ao longo do tempo de simulação.
A segunda etapa consistiu na análise da dependência da carga de prensagem com
a geometria da matriz e as condições de atrito. Assim, a partir dos deslocamentos impostos
sobre a parte superior do tarugo em cada configuração da matriz foram obtidas as curvas
força de reação-deslocamento para os nós situados no topo da amostra.
132
A terceira etapa caracterizou-se pela realização de um mapeamento nodal a partir
dos esquemas mostrados na Figura 87 com o intuito de avaliar a distribuição das
deformações plásticas efetivas ao longo da peça deformada em função da geometria da
matriz e dos níveis de atrito. O procedimento adotado foi similar ao exibido na Figura 84,
ou seja, foram escolhidos 4 pares de nós ao longo das direções vertical e horizontal e os
resultados foram dispostos com relação às distâncias relativas entre estes pontos.
(a)
(b)
Figura 87: Esquemas para o mapeamento nodal da distribuição das deformações
plásticas efetivas ao longo da superfície deformada do tarugo. (a) Φ = 90º e (b) Φ =120º.
4.2.3.4 Comparação entre modelos bidimensionais e tridimensionais
O objetivo central destas simulações foi verificar a validade dos modelos
bidimensional na condição de deformação plana aplicados ao estudo da prensagem de
tarugos via a técnica PCEA quando se atribui ao material deformado um encruamento do
tipo isotrópico associado ao critério de plasticidade de von Mises. A partir de geometrias
idênticas de matriz e mesmas condições de simulação, desenvolveu-se um modelo
tridimensional e as previsões numéricas de carga fornecidas por ambos os modelos após
um único passe de conformação foram comparadas aos resultados experimentais
conduzidos a partir do aparato apresentado na Figura 69.
Em concordância com a matriz empregada nos ensaios, o seu modelo numérico
constituiu-se de corpos elasto-rígidos com propriedades de um aço ferramenta H13 com
E = 200 GPa e ν = 0,3. Em todos os modelos foram considerados canais com 10 mm de
largura interceptados a 90º. A Figura 88 mostra os modelos 2D e 3D utilizados nas
simulações nos quais se pode observar a presença do raio de adoçamento externo, cujo
valor adotado foi de 5 mm com centro localizado nos pontos O. As condições de contorno
empregadas em todos os casos foram as restrições de movimentos ao longo dos eixos
cartesianos X, Y e Z.
133
(a)
(b)
Figura 88: Matrizes utilizadas na comparação entre modelos de simulação da técnica
PCEA. (a) bidimensional em condição de deformação plana e (b) tridimensional.
Para os tarugos adotou-se o comportamento elasto-plástico com encruamento
descrito segundo a lei de Hollomon associada às propriedades referentes à liga Al 1100
mostradas na Tabela 3. A extrapolação da curva de encruamento atingiu um máximo de
116% de deformação plástica efetiva. Ainda, as propriedades elásticas adotadas foram
E ≈ 69 GPa e ν = 0,33. As dimensões consideradas no modelo 2D foram
50 mm x 9,8 mm x 1mm (altura x largura x espessura) enquanto que no caso 3D se
utilizou uma peça de seção quadrada de 9,8 mm e mesma altura.
Na discretização dos tarugos e matrizes foram utilizados os elementos
PLANE 182 (2D) e SOLID 185 (3D) ambos dotados de integração completa. Às matrizes
o comprimento dos elementos foi de 2 mm. Aos tarugos assumiram-se elementos com
1 mm de lado fornecendo um número total de 500 ao caso 2D e 5.000 elementos ao
modelo tridimensional.
Em relação aos contatos peça-ferramenta, o tipo flexível com superfícies alvo para
a matriz e contato para o tarugo foram considerados. A discretização das interfaces no
modelo bidimensional envolveu a utilização dos elementos TARGE 169 e CONTA 171 e,
no caso 3D foram os TARGE 170 e CONTA 173. O algoritmo de contato adotado foi o
método de Lagrange aumentado associado à rotina TAUMAX.
134
As condições de atrito consideradas foram comuns aos modelos desenvolvidos e
representaram a situação de lubrificação ideal com µ = 0,05. A tensão limite de
escoamento a 0,2% de deformação plástica verdadeira foi 26,27 MPa e resultou no valor de
15,19 MPa para TAUMAX calculado com a Equação (177).
A pressão exercida pelo punção sobre a parte superior da amostra, para o caso 2D,
foi representada por incrementos compressivos de 0,5 mm de deslocamento ao longo do
eixo Y até um total de 45 mm de altura. No modelo tridimensional os deslocamentos foram
impostos de forma mais suave com incrementos de 0,25 mm até o máximo de 45 mm.
Nestas simulações utilizou-se o método completo de Newton-Raphson associado ao
método “line search”.
O pós-processamento adotado para ambos os modelos envolveu a determinação
das curvas de carga por meio das reações nodais observadas na porção superior dos
tarugos. Em seguida as previsões numéricas foram comparadas aos resultados
experimentais para a validação dos modelos e a confirmação da aproximação deste
problema ao estado plano de deformações. Por fim, realizou-se a comparação entre as
geometrias deformadas e a distribuição de tensões e deformações plásticas efetivas.
135
5. RESULTADOS E DISCUSSÃO
Este capítulo compreende a apresentação e discussão dos resultados obtidos
conforme a seqüência descrita em detalhes no CAPÍTULO 3. MATERIAIS E MÉTODOS
e se divide em seis partes.
A primeira parte apresenta a discussão acerca da influência de parâmetros
geométricos, tribológicos e critérios de escoamento plástico sobre as previsões analíticas
de pressão normalizada oriundas da prensagem da liga Al 6070 buscando mostrar a
existência de um acoplamento entre o critério de plasticidade e o atrito, responsável pelo
aumento de carga. Em seguida, são analisados os efeitos geométricos do ferramental sobre
as previsões teóricas de deformações plásticas efetivas. Por fim, os modelos propostos
foram validados a partir da comparação entre as previsões analíticas de carga calculadas a
partir dos critérios de plasticidade de Drucker e von Mises e o resultado experimental
oriundo do processamento da liga Al 1100.
A segunda parte se refere à comparação entre previsões de força fornecidas pelos
modelos numéricos propostos com os resultados experimentais determinados por
Eivani et al. [43-44]. Ao mesmo tempo a forma das curvas numéricas é explicada em
termos da condição de plasticidade por meio da comparação entre as curvas de
encruamento e das grandezas plásticas efetivas de tensão e deformação.
A terceira parte diz respeito à discussão acerca da classificação qualitativa de
efeitos geométricos da matriz, escoamento plástico, condições de atrito e velocidades de
prensagem sobre as previsões de pressão e deformações plásticas efetivas. Os resultados
desta etapa foram obtidos a partir das análises de variância baseadas do método fatorial 26
de planejamento de experimentos.
136
A quarta parte envolve a discussão voltada à validação das soluções propostas
para o cálculo da carga de prensagem necessária ao processamento de materiais que
exibem sensibilidade à taxa de deformação. Para tanto, são realizadas comparações entre
previsões teóricas e numéricas de carga e deformações efetivas.
A quinta parte de resultados abrange as análises numéricas para a determinação
das condições críticas de atrito nas quais não se observa a ocorrência de aderência nas
interfaces de contato peça-ferramental. Além disso, os efeitos do atrito sobre as previsões
numéricas de carga e distribuição homogênea de deformações plásticas efetivas ao longo
da superfície deformada do tarugo processado são também avaliados.
A última parte deste capítulo se destina à comprovação da eficiência de modelos
numéricos bidimensionais aproximados ao estado plano de deformações no estudo de
materiais deformados via a técnica PCEA. Para esta finalidade, as previsões de carga e
grandezas plásticas efetivas de tensão e deformação foram comparadas aos resultados
fornecidos por modelos tridimensionais e pelo experimento de prensagem da liga Al 1100.
5.1 EXPLORAÇÃO DOS MODELOS ANALÍTICOS PROPOSTOS
A Figura 89 mostra a sensibilidade da pressão normalizada (p/σy) e da tensão
efetiva aos parâmetros de geometria da matriz (Rint, Rext e Φ) para uma condição fixa de
atrito (m = 0,08) e considerando o critério de plasticidade isotrópico de von Mises. Pode-se
notar a extrema influência exercida pelo ângulo Φ sobre tais previsões de modo que seu
aumento no intervalo considerado 90º ≤ Φ ≤ 135º promoveu uma considerável queda tanto
de pressão normalizada como da tensão efetiva, mesmo com variações sobre os raios de
adoçamento da matriz. Este comportamento concorda plenamente com as observações
feitas por Eivani et al. [43] de que a forte dependência da carga com o ângulo Φ independe
dos valores atribuídos aos raios de adoçamento, já que o material é deformado ao
atravessar a zona de deformações localizada na região de interseção dos canais, mesmo em
ausência de adoçamentos. A magnitude da queda de pressão normalizada é muito próxima
em ambos os casos apresentados na Figura 89, ou seja, assumindo-se uma matriz composta
somente pelo raio de adoçamento externo igual a 5 mm, quando Φ aumentou de 90º para
135º, a pressão normalizada decresceu de 2,10 para 1,53 no caso da Figura 89a e de
1,94 para 1,39 no caso da Figura 89b. Portanto, pode-se confirmar que a relação entre a
pressão normalizada e Φ independe do arranjo dos canais, uma vez que para cada caso a
diferença entre as previsões foi praticamente idêntica e da ordem de 0,6.
137
Os efeitos individuais dos raios de adoçamento sobre as previsões de pressão
normalizada revelaram comportamentos distintos, em concordância com os resultados de
σy (Figuras 89c e 89d). O aumento de Rint no intervalo 0 mm ≤ Rint ≤ 5 mm conduziu à
elevação de p / σy de 2,10 para 2,27 assumindo-se Φ = 90º, já que induz à queda das
previsões de β e, por conseguinte, do termo trigonométrico que envolve o seno deste
ângulo. Portanto, a queda de β implicou no aumento da pressão normalizada.
(a)
(b)
(c)
(d)
Figura 89: Dependência entre p / σy e a geometria da matriz. (a) Φ e Rint e (b) Φ e Rext.
Relação entre σy e a geometria da matriz. (c) Φ e Rint e (d) Φ e Rext.
O raio de adoçamento externo, por sua vez, promoveu uma queda de pressão
normalizada no intervalo entre 2,21 ≤ p / σy ≤ 1,94 ao se variar este parâmetro até 5 mm
também para Φ = 90º, já que conduz ao aumento de β e a diminuição de σy (Figura 89d).
As previsões analíticas obtidas por Eivani et al. [43] evidenciaram um decréscimo da
pressão normalizada associado ao aumento de Rext. Comparando-se os efeitos causados
pelos raios de adoçamento sobre a pressão normalizada, observou-se uma maior influência
de Rint. Assim, matrizes dotadas de pequenos raios de adoçamento interno apresentam
benefícios em termos de carga e o aumento do raio externo contribui no mesmo sentido.
138
A Figura 90 mostra os efeitos combinados entre as condições de atrito e os
parâmetros geométricos da matriz. Em todos os casos considerou-se o raio de adoçamento
externo constante e igual a 5 mm e o escoamento plástico definido pelo critério de von
Mises. Ao se avaliar os efeitos promovidos pelo ângulo Φ e as condições de atrito (fator m)
para um arranjo fixo dos raios de adoçamento (vide Figura 90a) pode-se verificar o papel
primário desempenhado por este último parâmetro. Utilizando como exemplo a condição
de lubrificação ideal (m = 0,08), a pressão normalizada diminuiu de 1,93 para 1,39 quando
o ângulo Φ se elevou de 90º para 135º. Entretanto, assumindo-se Φ = 90º e variando-se m,
a elevação da pressão normalizada foi de 1,93 para 5,61. Estes valores apresentados
mostram que o aumento de Φ promove uma queda próxima a 28% sobre as previsões de
p / σy. Em contrapartida, partindo-se da lubrificação ideal (m = 0,08) para a condição de
atrito severo (m = 0,40) a pressão normalizada apresentou um aumento da ordem de 291%.
Isto reforça o caráter de dependência entre a carga de prensagem e as condições de atrito.
O nível máximo de pressão normalizada foi alcançado pela combinação entre os
efeitos dos raios de adoçamento e condições de atrito, conforme mostrado na Figura 90b.
Assim, o valor obtido foi 5,75 para o caso em que Φ = 90º e Rint/Rext = 1,0 juntamente com
m = 0,40. À parte o efeito promovido pelo atrito, explica-se este comportamento pelo fato
de que o aumento de Rint contribui para a elevação de p / σy, como discutido previamente,
já que Rext se manteve inalterado. Ainda, Pérez [39] observou que materiais deformados
através de matrizes com raios de adoçamentos iguais requerem cargas maiores devido à
reação imposta sobre o tarugo pela matriz, associada à presença do adoçamento interno.
4,600
p / σy
5
5,600
4
κ/σy = 0,58
3
Rint = 0,00 mm
Rext = 5,00 mm
2
4,000
5,500
5
5,800
4
κ/σy = 0,58
3
Φ
= 90º
Rext = 5,00 mm
2
0,40
0,32
0,24
135
m
ito
,
1
0
0,16
R /
int R
ext
0,08
1
Fa
0,08
Fa
raus 120
)
Φ (g
to
r
0,16
105
de
1
90
at
rit
o,
m
0,40
0,32
0,24
2,500
6
at
r
3,400
de
6
1,900
7
to
r
2,200
p / σy
1,300
7
(a)
(b)
Figura 90: Dependência de p / σy com a geometria da matriz e as condições de atrito.
(a) Φ e m e (b) Rint / Rext e m.
139
A Figura 91 mostra a influência dos critérios de Drucker (κ / σy = 0,54) e
von Mises (κ / σy = 0,58) associados à configuração da matriz e às condições de atrito
sobre a pressão normalizada. É possível notar que, fixando-se os raios de adoçamento e
adotando-se a lubrificação ideal (Figura 91a), o ângulo Φ exerceu um efeito mais
importante que as curvas de escoamento embora o critério de Drucker permita uma melhor
descrição do comportamento de materiais cúbicos de face centrada entre os estados de
compressão plana e cisalhamento puro. Dessa forma, aumentando-se Φ de 90º para 135º a
pressão normalizada orientada no sentido do critério de Drucker diminuiu de 1,82 a 1,31,
que se traduz em uma queda próxima a 28%. Todavia, variando-se o critério de
escoamento e assumindo-se Φ = 90º houve um acréscimo da pressão normalizada de 1,82
para 1,93, ou seja, de 6%.
1,300
7
6
2,200
6
1,940
5
5
m = 0,08
Rint = 0,00 mm
0,58
1
0,56
0
R /
int R
κ
105
Φ (g
2
/σ
0,56
3
120
raus
)
135
0,54
e xt
(a)
y
1
90
Rext = 5,00 mm
0,58
/σ
2
Φ
4
κ
3
= 90º
m = 0,08
Rext = 5,00 mm
p / σy
4
y
p / σy
1,800
7
1,750
1
0,54
(b)
1,800
7
2,714
3,571
6
4,429
5,286
p / σy
5
5,700
4
= 90º
m = 0,08
Rext = 5,00 mm
Φ
3
2
ea
tr
it o
,m
0,58
to
y
0,08
rd
0,16
0,56
κ/σ
Fa
0,54
0,40
0,32
0,24
1
(c)
Figura 91: Dependência de p / σy com os critérios de escoamento, geometria da matriz e
o atrito. (a) Φ e κ / σy; (b) Rint / Rext e κ / σy e (c) m e κ / σy.
140
Associando-se os efeitos dos critérios de escoamento aos raios de adoçamento
sobre a pressão normalizada (Figura 91b) observou-se novamente que o raio interno
contribuiu para o aumento de carga e que este comportamento se mostrou comum a ambos
os critérios. Obviamente que o critério de von Mises foi responsável pelos maiores níveis
de pressão observados, ou seja, 1,93 ≤ p / σy ≤ 2,18 quando 0 ≤ Rint/Rext ≤ 1. Por outro
lado, o critério de Drucker forneceu um aumento de pressão de 1,82 para 2,05.
A Figura 91c revela o acoplamento entre a tribologia e o escoamento plástico a
partir da análise conjunta dos efeitos de atrito e escoamento do material sobre a pressão
normalizada. Em outras palavras, o aumento do fator de atrito ou a utilização do critério de
von Mises ao invés da relação proposta por Drucker resultam na elevação da carga, embora
as condições de atrito exerçam maior influência. Considerando-se que o acoplamento entre
o critério de plasticidade e o atrito se constitua em um fenômeno presente em processos de
conformação que envolvem o escoamento plástico do material deformado, os estudos
teóricos mais recentes voltados à proposição de soluções analíticas para os cálculos de
carga e das deformações plásticas efetivas se limitam à definição isotrópica fornecida pelo
critério de von Mises. Dentre os trabalhos mais recentes sobre o tema PCEA que se
incluem nesta limitação observam-se àqueles desenvolvidos por Pérez e Luri [45] e
Paydar et al. [80]. O critério de Drucker, por considerar a constante c relacionada a
parâmetros materiais, apresenta uma descrição mais abrangente do comportamento plástico
da peça deformada.
A Figura 92 apresenta a influência da configuração da matriz sobre as previsões
de deformações plásticas efetivas (ε) calculadas a partir das soluções geométricas e
independentes das condições de atrito propostas por Luri et al. [89], definidas nas
Equações (166) e (167). Além disso, cabe ressaltar que os critérios de escoamento
empregados fornecem correções idênticas para tal solução no estado de cisalhamento puro.
Assim, o comportamento destas soluções revela a maior dependência de ε com o ângulo Φ
do que com os raios de adoçamento.
A presença de Rint se mostrou benéfica e acabou por elevar as previsões de
deformação plástica efetiva (vide Figura 92a). Sendo assim, para Φ = 90º as deformações
plásticas efetivas impostas ao material aumentaram de 1,03 a 1,15 para o intervalo
0 mm ≤ Rint ≤ Rext. Contudo, de acordo com as discussões acerca da Figura 89, este
procedimento não é interessante por acarretar um acréscimo de pressão.
141
O raio de adoçamento externo foi responsável por um decréscimo de ε que variou
de 1,15 para 1,04 quando 0 ≤ Rext ≤ 5 mm (Figura 92b). Portanto, no que se refere às
deformações plásticas efetivas os efeitos causados por alterações efetuadas sobre os raios
de adoçamento são proporcionais. Esta característica é esperada já as soluções propostas
não consideram a influência do atrito sobre a deformação plástica efetiva.
Associando-se o comportamento das soluções voltadas ao cálculo da deformação
plástica efetiva frente às alterações consideradas na geometria da matriz e as previsões de
pressão normalizada, pode-se sugerir, do ponto de vista experimental, que o emprego de
um ferramental constituído por somente o raio de adoçamento externo igual a 5 mm se
mostra satisfatório. Esta configuração se caracteriza por níveis relativamente elevados de
deformação plástica efetiva por passe de prensagem e, quando associado à condição de
atrito próxima da lubrificação ideal, resulta em um decréscimo da carga de prensagem. Em
relação às previsões de carga, a descrição do comportamento plástico no sentido do critério
de Drucker possibilita uma maior flexibilidade em relação ao critério de von Mises.
(a)
(b)
Figura 92: Dependência entre as deformações plásticas efetivas e os parâmetros
geométricos da matriz. (a) ângulo Φ e Rint (b) ângulo Φ e Rext.
142
5.1.1 Validação dos modelos analíticos propostos
A Figura 93 compara as previsões de carga fornecidas pelos modelos analíticos
com o resultado experimental obtido após a prensagem a frio, em um único passe, da liga
Al 1100 em condições de lubrificação ideal (m = 0,08). A matriz utilizada possui um raio
de adoçamento externo de 5 mm e canais interceptados a Φ = 90º. Ainda, os efeitos do
escoamento plástico sobre a carga foram investigados por meio dos critérios de
plasticidade de von Mises e Drucker.
De uma forma geral, o caráter conservativo associado ao método do limite
superior se manteve, uma vez que ambas as previsões analíticas de carga se mantiveram
acima do resultado experimental. Entretanto, comparando-se as previsões de carga
fornecidas pelos critérios de plasticidade adotados ao experimento, observa-se que a
descrição de von Mises resultou em um acréscimo de carga igual a 9,4%. Por outro lado, o
critério de plasticidade de Drucker reduziu a diferença entre as previsões teórica e
experimental para apenas 3,2%. De fato, este último critério leva em conta o parâmetro c
associado ao arranjo cristalino dos metais que possuem simetria cúbica (CCC ou CFC), e
exibe um achatamento sobre a respectiva superfície de escoamento nas regiões de
cisalhamento puro e deformação plana por compressão que a desloca para uma posição
intermediária às superfícies de Tresca e von Mises. Este aspecto induz à queda da tensão
de escoamento do material, reduzindo a correção κ/σy e a carga de prensagem.
60
Força (kN)
50
40
30
presente trabalho - critério de von Mises
presente trabalho - critério de Drucker
Experimental - liga Al 1100
Φ = 90º
m = 0,08 ; µ = 0,05
Rint = 0,00 mm; Rext = 5,00 mm
25,16
23,73 23,00
20
10
0
38
β (graus)
Figura 93: Validação dos modelos propostos para o cálculo da carga de prensagem.
143
5.2 SIMULAÇÃO COMPUTACIONAL DA LIGA DE ALUMÍNIO Al 6070
5.2.1 Efeito da curva de encruamento
A Figura 94 apresenta a comparação entre as curvas experimental, obtida por
Eivani et al. [43], e numéricas de carga para a liga de alumínio Al 6070 deformada em uma
matriz com Φ = 90º sem raios de adoçamento considerando-se as mesmas condições de
atrito (m = 0,18). As previsões numéricas foram obtidas via o método dos elementos finitos
a partir de modelos aproximados à deformação plana. Buscando avaliar os efeitos do
encruamento do material foram adotados os valores máximos de 1,16 e 0,26 para a
deformação plástica efetiva, correspondentes à previsão calculada com a Equação (166) e
ao expoente de encruamento do material, respectivamente.
Segundo Eivani et al. [43], a curva experimental mostra um aumento inicial de
carga com o movimento do punção (O até A) pela compressão exercida sobre a base do
tarugo. É importante ressaltar que a região OA define a passagem da base do tarugo em
direção ao canal de saída da matriz, em condições de compressão plana. Em seguida, a
força se intensifica de A até um máximo local em B (~70 kN) em B em razão da alta taxa
de encruamento associada à plastificação da peça. Após o ponto B, há uma queda de carga
até C em virtude da restrição imposta pelo canal de saída, a qual, por sua vez, conduz a um
forjamento do tarugo. Os autores ressaltaram também que o processo de prensagem é
governado pelo atrito estático desde o ponto O até B, ao passo que entre B e C prevaleceu
uma condição dinâmica de atrito responsável pelo pequeno decréscimo de carga. A partir
do ponto C ocorreu um aumento de carga associado a uma taxa de encruamento menor
(C a D) que se estendeu até o fim do processo (ponto E).
90
Φ = 90º
80
70
Força (kN)
m = 0,18
Rint = Rext = 0,00 mm
A
60
B
50
A'
C
D
40
B'
30
C'
20
10
0
E
O
0
Máxima def. plástica efetiva: 1,16
Máxima def. plástica efetiva: 0,26
5 10 15 20 25 30 35 40 45 50 55 60 65 70
Deslocamento do tarugo (mm)
(a)
(b)
Figura 94: Comparação entre as curvas de prensagem para a liga Al 6070.
(a) experimental [43] e (b) 2D numéricas relacionadas à máxima def. plástica efetiva.
144
As curvas obtidas por meio da simulação computacional, vide Figura 94b,
revelaram comportamentos distintos que estão diretamente relacionados aos níveis
máximos de deformação plástica efetiva que se referem a cada curva de encruamento
representativa do comportamento plástico do material. No caso em que ε = 1,16 observa-se
um rápido aumento de carga (O até A) após cerca de 5 mm de deslocamento até o máximo
de 68 kN, comparável ao resultado experimental obtido por Eivani et al. [43] de 70 kN
após 16 mm.
A previsão numérica máxima de força de prensagem foi obtida a partir de um valor
de deslocamento três vezes menor que o resultante do teste experimental devido à hipótese
de encruamento isotrópico definido segundo o critério de von Mises, o qual não considera
qualquer parâmetro material. Além disso, a utilização de uma curva de encruamento obtida
por meio de ensaios de compressão uniaxial, apesar de fornecer resultados de carga
comparáveis aos experimentos, é limitada para representar a prensagem em canais
equiangulares, frente aos elevados níveis de deformação plástica efetiva atribuídos ao
material após cada passe, em condições de cisalhamento. Melhores resultados, mesmo ao
se adotar o critério de von Mises, seriam obtidos ao se empregar uma curva de
encruamento obtida por de ensaios de torção.
O rápido aumento de carga mostrado pela simulação até o ponto A pode ser
explicado pela compressão plana experimentada pelo material ao ser forçado a escoar em
direção ao canal de saída da matriz, como sugeriram Eivani et al. [43]. Entretanto, uma
análise extremamente útil a este caso é a verificação da condição de plasticidade pela
comparação entre as curvas de encruamento com as grandezas efetivas tensão-deformação
plástica determinadas em função do critério de plasticidade adotado. A Figura 95 apresenta
tal comparação, a qual evidencia que o carregamento plástico ocorre somente no início da
prensagem, ou seja, após cerca de 5 mm de deslocamento do punção. Neste intervalo de
deslocamento as tensões da curva de encruamento e aquelas do critério de von Mises se
igualam, o que constitui a condição de um comportamento elasto-plástico. O que se
observa após 5 mm de deslocamento é a condição de descarregamento elástico que se
estende até o final da simulação, na qual as previsões do critério de von Mises estão abaixo
dos valores da lei de encruamento de Hollomon.
145
Deslocamento do tarugo (mm)
Deslocamento do tarugo (mm)
Tensão efetiva (MPa)
240
200
160
280
Critério de von Mises
Curva de encruamento
Φ = 90º
m = 0,18
240
β = 0º
εmáx = 1,16
Tensão efetiva (MPa)
280
0 6 12 18 24 30 36 42 48 54 60 66 72 78 84 90
120
80
40
0
200
160
0 6 12 18 24 30 36 42 48 54 60 66 72 78 84 90
Critério de von Mises
Curva de encruamento
Φ = 90º
m = 0,18
β = 0º
εmáx = 0,26
120
80
40
0
0,0
0,2
0,4
0,6
0,8
1,0
Deformação plástica efetiva
1,2
1,4
0,0
0,2
0,4
0,6
0,8
1,0
Deformação plástica efetiva
1,2
1,4
(a)
(b)
Figura 95: Condição de plasticidade referente à prensagem da liga Al 6070.
(a) ε = 1,16 e (b) ε = 0,26 .
É interessante também observar as etapas de deformação do tarugo. A Figura 96
mostra que o início da curvatura do tarugo resulta em seu descolamento e, por conseguinte,
em uma queda inicial de carga a partir de A até B, conforme mostrado na Figura 94b.
Do ponto B até a completa passagem da base do tarugo para o canal de saída da matriz,
vide ponto C, há um progressivo aumento na curvatura do material e o aparecimento de
regiões de perda de contato entre o tarugo e a porção superior do canal de saída da matriz,
conforme mostrado na Figura 96b. Estes efeitos combinados ao descarregamento elástico
provocaram o decréscimo de carga observado no ponto C.
(a)
(b)
Figura 96: Regiões de descolamento e perda de contato entre o tarugo e a matriz.
(a) após 5 mm deslocamento e (b) após 14 mm de deslocamento.
146
Em seguida, o comportamento que se inicia no ponto D e se estende até o ponto E,
é caracterizado por uma queda contínua de carga de prensagem. Até cerca de 30 mm,
o descarregamento elástico associado às regiões de perda de contato entre o tarugo e a
matriz podem ser considerados como os principais responsáveis pela diminuição de carga.
Contudo, ao se verificar a dependência das deformações plásticas efetivas com os
deslocamentos impostos ao material é possível notar que após 30 mm ocorreu a sua
saturação em torno do valor médio de 1,06 (Figura 97a). Este valor médio reflete a máxima
deformação plástica efetiva permitida na extrapolação da curva de encruamento
introduzida no modelo numérico. Do ponto de vista da simulação computacional, a
saturação tem o significado de incrementos nulos de deformação plástica entre iterações
numéricas sucessivas, os quais explicam a queda das tensões efetivas relativas ao critério
de escoamento (Figura 95b). Portanto, os valores de carga obtidos após a saturação estão
associados às parcelas elásticas de deformação que são extremamente baixas.
É imprescindível destacar que a curva experimental obtida por Eivani et al. [43]
apresenta um aumento de carga desde C até o ponto E, vide Figura 94a, sendo este último
considerado o local de máximo valor de força (~ 88 kN). Todavia, como a carga máxima
fornecida pela simulação é comparável ao ponto experimental B, considerou-se validado o
modelo numérico a partir deste resultado experimental. Possivelmente, o acréscimo
progressivo de carga pode estar relacionado a problemas durante a realização dos ensaios,
como por exemplo, a penetração do punção em regiões dos canais da matriz.
O segundo caso considerado, no qual o expoente de encruamento obtido para a liga
Al 6070 delimitou o nível máximo de deformações plásticas efetivas permitido durante a
simulação, apresentou um considerável decréscimo sobre a carga máxima de prensagem
quando comparada à condição anterior, já que a capacidade de encruamento do material
diminuiu. O valor encontrado foi de ~ 46 kN sobre o ponto A’ mostrado na Figura 94b, o
qual resultou em uma queda de 32,4 % em relação ao valor de 68 kN obtido quando
ε = 1,16 . A curva força x deslocamento mostrou um comportamento similar ao caso
referente à máxima deformação efetiva de 1,16 ao longo da região compreendida entre os
pontos O e A’, caracterizado pelo rápido aumento de carga após 3 mm de deslocamento.
Da mesma forma, este aumento é explicado pela condição de plasticidade apresentada na
Figura 95b. No entanto, a menor capacidade de endurecimento atribuída ao material
quando ε = 0,26 conduziu ao decréscimo das previsões de tensão efetiva e à obtenção da
carga máxima em um deslocamento menor.
147
A forma mais suavizada da curva tensão x deformação efetiva está relacionada às
extrapolações realizadas pelo programa Ansys® no cálculo dos incrementos de deformação
plástica efetiva impostos ao tarugo entre as iterações, de forma a atribuir-lhe quantidades
satisfatórias de deformação após um único passe de prensagem.
A capacidade reduzida de encruamento tornou menos severa e sob a forma de
rampa a curvatura do material a partir do ponto A’ até B’, ao contrário dos degraus
observados no caso anterior (região compreendida de A a C). A região que se estendeu de
B’ a C’ foi também marcada por um decréscimo contínuo, embora mais suave, de carga
que se justifica pelo descarregamento elástico e a saturação das deformações plásticas
efetivas após 30 mm de deslocamento. Vale ressaltar que a saturação ocorreu a um valor
médio de 1,16, o qual é aproximadamente 9 % maior que o resultado igual a 1,06 fornecido
previamente. A Figura 97b apresenta a referida curva de deformação plástica
efetiva x deslocamento do tarugo, na qual se pode confirmar a característica de que o
material dotado de menor capacidade de encruamento se deformou mais a um dado valor
de deslocamento, por comparação à Figura 97a.
1,4
1,4
Φ = 90º
β
= 0º
εmax = 1,16
1,0
1,2
Def. plástica efetiva
Def. plástica efetiva
1,2
0,8
0,6
0,4
0,2
0,0
1,0
Φ = 90º
= 0º
β
εmax = 0,26
0,8
0,6
0,4
0,2
0,0
0
5 10 15 20 25 30 35 40 45 50 55 60 65 70
Deslocamento do tarugo (mm)
(a)
0
5 10 15 20 25 30 35 40 45 50 55 60 65 70
Deslocamento do tarugo (mm)
(b)
Figura 97: Curvas de deformação plástica efetiva. (a) ε = 1,16 e (b) ε = 0,26 .
A Figura 98 mostra a distribuição das deformações plásticas efetivas ao longo das
superfícies dos tarugos modelados pelas distintas curvas de encruamento consideradas. O
material com menor nível de encruamento revela uma distribuição mais homogênea ao
longo da superfície em verde claro, estendendo-se nas porções médias da amostra. Porém,
neste caso o tarugo foi submetido a quantidades maiores de deformação. O material com
maior capacidade de encruamento exibiu maior grau de heterogeneidade ao longo da
superfície deformada em verde escuro.
148
Além disso, há uma redução sobre os valores de deformação plástica efetiva ao
longo desta região. De fato, conforme mostrado na Figura 98d, a distribuição das tensões
efetivas mostrou que a menor capacidade de encruamento acabou por estender a região de
máximas previsões (em vermelho) ao longo da peça, caracterizando a homogeneidade das
deformações plásticas efetivas. Já o material com maior capacidade de endurecimento
apresentou uma zona de previsões máximas de tensão efetiva, vide Figura 98c, com menor
extensão devido à maior curvatura exibida junto às porções inferiores da matriz. Dessa
forma, a distribuição das deformações plásticas efetivas ao longo da superfície deformada
da peça se tornou mais heterogênea, uma vez que esta sua extensão está diretamente ligada
às dimensões da região de maiores previsões de tensão efetiva.
(a)
(b)
(c)
(d)
Figura 98: Distribuição das grandezas plásticas efetivas. (a) e (c) deformação e tensão
para ε max = 1,16 ; (b) e (d) deformação e tensão para ε max = 0,26 .
A simulação de um único passe de prensagem da liga Al 6070 com menor
capacidade de endurecimento pode conduzir à interpretação equivocada de que este
procedimento está correto, uma vez que o material é submetido a níveis maiores de
deformação plástica efetiva em um menor valor de deslocamento e apresenta uma
distribuição mais uniforme deste parâmetro ao longo da superfície média deformada do
tarugo. Entretanto, as previsões de carga oriundas desta metodologia apresentaram uma
redução significativa em relação ao caso em que se atribuiu a curva de encruamento
condizente com o primeiro ciclo de prensagem e até quando comparada ao experimento.
Por tais razões, em todas as simulações que serão apresentadas posteriormente adotar-se-á
a extrapolação das curvas de encruamento até o valor máximo de ε com o intuito de evitar
problemas relacionados às previsões de carga necessária à prensagem dos materiais
utilizados.
149
5.2.2 Efeitos geométricos da matriz
A Figura 99 compara a curva experimental força de prensagem e deslocamento do
punção obtida por Eivani et al. [43] com a previsão numérica por elementos finitos para
um único passe da liga Al 6070, obtida para uma matriz canais interceptados a Φ = 90º,
provida de raio de adoçamento externo e sob as mesmas condições de atrito. De acordo
com Eivani et al. [43], a presença de raios de adoçamento externos no ferramental torna
mais complexa a identificação e diferenciação do ponto máximo de força em relação às
demais regiões observadas ao longo da curva experimental mostrada na Figura 99a.
A justificativa apresentada para tal afirmação se apóia no fato de que esta
geometria oferece uma restrição menor ao movimento do tarugo em direção ao canal de
saída quando comparada a uma matriz sem adoçamentos. Por esta razão, a carga máxima
experimental observada na Figura 99a foi de cerca de 63 kN e representou um decréscimo
de 7,4% em relação aos 68 kN obtidos sem os adoçamentos. A curva experimental
mostrada na Figura 99a apresenta um comportamento similar ao caso anterior, ou seja, um
aumento gradual de carga no domínio do atrito estático (O até B) seguido por uma alta taxa
de encruamento (A para B). A parcela dinâmica de atrito promove igualmente uma
pequena queda de carga entre os pontos B e C. A partir do ponto C houve um aumento de
carga que se estendeu até o ponto E.
80
Φ = 90º
70
m = 0,18
Força (kN)
60
B"
50
C"
40
30
D"
A"
20
10
0
O
0
5 10 15 20 25 30 35 40 45 50 55 60 65 70
Deslocamento do tarugo (mm)
(a)
(b)
Figura 99: Curvas de prensagem carga-deslocamento para a liga Al 6070.
(a) experimental [43] e (b) 2D numérica.
150
Por outro lado, a curva de carga obtida por meio da simulação computacional,
revela a existência de três estágios distintos. O primeiro estágio se caracteriza por um
aumento de carga ao longo da região OB”, resultante da combinação entre as trajetórias
OA” e A”B”. A trajetória OA” compreende o ajuste da base do tarugo ao raio externo de
forma a se moldar a este arranjo dos canais. Esta conformação envolve uma espécie de
forjamento do material, destacado em vermelho na Figura 100a, durante cerca de 7 mm,
o que eleva a carga para cerca de 23 kN em boa concordância com a curva experimental.
Em seguida, a trajetória A”B” indica a continuação do forjamento seguida pela deformação
por compressão plana devido ao contato entre a base já endurecida do tarugo e a região
inferior do canal de saída da matriz, conforme apresentado na Figura 100b. Pelo rápido
aumento de carga de 23 kN para cerca de 49 kN após 3 mm de deslocamento do tarugo, o
modelo numérico reproduziu a alta taxa de endurecimento observada por Eivani et al. [43].
(a)
(b)
(c)
Figura 100: Estágios de deformação associados à prensagem através de matrizes com
adoçamento externo. (a) forjamento, após 7 mm; (b) forjamento e compressão plana,
após 10 mm e (c) forjamento e compressão plana, após ~ 25 mm.
151
O segundo estágio, delimitado pelos pontos B” e C” indicados na Figura 99,
evidencia um pequeno aumento de carga de 49 kN para ~ 51 kN sobre C” após ~25 mm,
onde o ponto B pode ser identificado como sendo o máximo local da carga de prensagem.
Este leve acréscimo de força está associado ao dobramento do tarugo decorrente de sua
passagem sobre o adoçamento externo, o qual fez surgir uma pequena região de solicitação
sobre a matriz junto à porção superior do canal de saída, como destacado na Figura 100c.
Neste sentido, é mais condizente com o processo considerar a carga máxima no ponto B”.
O terceiro estágio, entre os pontos C” e D”, apresenta uma progressiva queda de carga que
se estende até o final do percurso do punção de 67 mm de deslocamento do tarugo.
A análise da condição de plasticidade para esta configuração da matriz,
apresentada na Figura 101a, permite comprovar que a região OB” mostrada na curva de
carga (Figura 99b) delimita o comportamento plástico do material, já que as tensões
efetivas de encruamento e do critério de von Mises se aproximam até 10 mm de
deslocamento do tarugo, ou seja, até o ponto B”. A partir deste ponto e até o final da
simulação observa-se o comportamento típico do descarregamento elástico, ou seja, as
previsões de tensão efetiva fornecidas pelo critério de escoamento são inferiores àquelas
provenientes da curva de encruamento para os mesmos níveis de deformação plástica
efetiva. Novamente, o descarregamento elástico foi o principal responsável pelo sucessivo
decréscimo de carga entre os pontos C” e D” até 35 mm de deslocamento do tarugo. A
partir de então, a combinação entre a saturação das deformações plásticas efetivas e os
efeitos de descarregamento promoveu um decréscimo de carga mais acentuado.
Deslocamento (mm)
Tensão efetiva (MPa)
240
200
160
0 6 12 18 24 30 36 42 48 54 60 66 72 78 84 90
Critério de von Mises
Curva de encruamento
Φ = 90º
m = 0,18
1,4
1,2
Def. plástica efetiva
280
β = 30º
εmáx = 1,16
120
80
1,0
Φ = 90º
β
= 30º
εmax = 1,16
0,8
0,6
0,4
0,2
40
0,0
0
0,0
0,2
0,4
0,6
0,8
1,0
1,2
Deformação plástica efetiva
1,4
0
5 10 15 20 25 30 35 40 45 50 55 60 65 70
Deslocamento do tarugo (mm)
(a)
(b)
Figura 101: (a) condição de plasticidade referente à prensagem da liga Al 6070 e (b)
deformações plásticas efetivas em função dos deslocamentos impostos.
152
A Figura 102 apresenta os efeitos promovidos pela geometria da matriz sobre as
previsões numéricas de força e deformações plásticas efetivas, considerando-se as mesmas
condições de atrito e Φ = 90º. No que diz respeito às previsões de carga de prensagem,
a presença do raio de adoçamento externo resultou em um máximo de 50 kN, ponto B”,
que se traduz em um decréscimo próximo a 26,5% em relação à previsão de 68 kN obtida
para a matriz sem raios, ponto A neste caso. Além disso, a comparação entre estas curvas
se mostrou útil para a comprovação de que os efeitos combinados entre o descarregamento
elástico e a saturação de deformação plástica efetiva podem explicar a queda de carga após
cerca de 25 mm de deslocamento do tarugo. É importante ressaltar ainda que a presença do
raio externo aumenta a distância a ser percorrida pelo tarugo até atingir a base da matriz e,
por conseguinte, um aumento no deslocamento necessário ao valor máximo de carga.
A comparação entre as previsões de deformação plástica efetiva, apresentada na
Figura 102b para ambas as geometrias de ferramental consideradas, mostrou a forma
sigmoidal comum às curvas obtidas. Assumindo como referência o caso sem adoçamentos,
esta similaridade se constituiu em uma forte evidência de que mesmo com a adição do
adoçamento externo o cisalhamento prevaleceu como o principal modo de deformação do
material, o que concorda plenamente com as observações reportadas acerca dos efeitos
geométricos do ferramental por Rosochowski et al. [78] e, mais recentemente, por
Dumoulin et al. [55]. Em relação aos valores máximos, a presença de adoçamento forneceu
ε max = 0,98 que representou um decréscimo de 7,6 % em comparação ao caso prévio.
1,4
80
B
D
C
B"
50
C"
40
E
30
D"
A"
20
10
O
0
0
Ausência de raios de adoçamento
β = 30º:Rint=0,00 mm;Rext=5,91 mm
5 10 15 20 25 30 35 40 45 50 55 60 65 70
Deslocamento do tarugo (mm)
(a)
β = 0º
β = 30º
1,2
m = 0,18
Def. plástica efetiva
60
Força (kN)
Φ = 90º
A
70
1,0
0,8
0,6
0,4
0,2
Φ = 90º
εmax = 1,16
0,0
0
5 10 15 20 25 30 35 40 45 50 55 60 65 70
Deslocamento do tarugo (mm)
(b)
Figura 102: Efeitos de geometria da matriz. (a) previsões força e (b) previsões de ε .
153
5.3 ANÁLISE FATORIAL 2k
5.3.1 Influência dos parâmetros considerados sobre a pressão e a deformação efetiva
A Tabela 10 apresenta as previsões analíticas de pressão e deformação plástica
efetiva para a liga de alumínio Al 6061, relativas a cada uma das combinações entre os
parâmetros considerados, as quais constituem o planejamento fatorial 26. Além disso, os
efeitos principais (A até F) e combinados calculados por meio da Equação (168) fazem
parte também da Tabela 10. A Tabela 11 mostra a classificação em ordem crescente dos
efeitos que atuam sobre a pressão ou a deformação plástica efetiva para a determinação da
probabilidade com que cada um exerce influência sobre as variáveis de interesse.
Em relação à pressão, a existência de 63 efeitos distintos e a combinação (1)
estabelece que o cálculo da probabilidade de cada efeito j seja definido por:
 (ordem − 0,5)
Pj = 
64


 100
(190)
onde a ordem denota o número associado a cada efeito.
A deformação plástica efetiva revelou um total de 14 efeitos j distintos além da
combinação (1). Portanto, as respectivas probabilidades Pj foram determinadas a partir de:
 (ordem − 0,5)
Pj = 
15


 100
(191)
Segundo Montgomery [77], ainda que a combinação (1) não produza efeitos sobre
as variáveis analisadas é necessário considerar a sua contribuição em ocasião do cálculo
das probabilidades para a correta interpretação do planejamento fatorial 2k utilizado. Além
disso, a incorreta determinação das probabilidades prejudica diretamente a análise de
variância destinada à verificação do grau de importância de cada parâmetro considerado,
uma vez que os gráficos probabilísticos são responsáveis pela identificação de sua
relevância.
154
Tabela 10 Pressão de prensagem e deformação efetiva oriundas do método fatorial 26.
155
Tabela 11 Classificação dos efeitos quanto à probabilidade (Pj) de relevância sobre as
previsões de pressão e deformações plásticas efetivas.
156
A Figura 103 apresenta os gráficos de probabilidade normal obtidos após os
cálculos efetuados sobre os efeitos promovidos por cada parâmetro sobre as soluções
analíticas voltadas às previsões de pressão e deformação plástica efetiva. Em relação à
pressão, é possível observar que os parâmetros principais Rext (A), Φ (C), κ / σy (D), m (E)
e V0 (F) e algumas combinações exercem influência por se localizarem externamente à
linha azul de regressão. Todavia, o parâmetro E, que corresponde ao fator de atrito m,
desempenha papel mais importante com valor de probabilidade próximo a 100%. Os
efeitos dos raios de adoçamento (A e AB), critérios de escoamento plástico (D) e
velocidade inicial de prensagem (F) apresentam relevância intermediária enquanto o
ângulo Φ (C) contribui em menor escala sobre a pressão, quando comparado ao fator de
atrito m.
No que se refere à deformação plástica efetiva, o caráter puramente geométrico
evidenciado nas Equações (166) e (167) é confirmado pelo gráfico de probabilidade. Neste
sentido, o efeitos individuais do ângulo Φ e dos raios de adoçamento e as combinações
entre os raios de adoçamento e Φ (AC e BC) foram identificados como relevantes em
virtude dos posicionamentos externos à linha azul de regressão. Dumoulin et al. [55] e
Yoon et al. [79] ressaltaram a influência exercida pelos raios de adoçamento sobre as
previsões e a homogeneidade das deformações plásticas efetivas oriundas da prensagem
1
4
6
90
7
20
80
30
1=E
2=D
3 = AB
4 = DE
5=F
6 = AC
40
50
60
70
80
90
100
100
7 = EF
8 = BCE
9=A
10 = CE
11 = ABC
12 = C
70
60
50
40
30
20
10
9
12
-400 -200
0
10
11
0
200 400 600 800 1000 1200 1400
Efeitos sobre a pressão
(a)
0
10
2
100
1
90
20
80
30
70
40
60
50
50
60
1=B
2 = AC
3 = BC
4=A
5=C
70
3
80
90
4
5
100
40
30
Prob x 100
10
5
8
Probabilidade Normal, (1- Prob) x 100
3 2
0
Prob x 100
Probabilidade Normal, (1- Prob) x 100
via a técnica PCEA, confirmando a validade dos resultados apresentados na Figura 103b.
20
10
0
-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5
Efeitos sobre a def. plástica efetiva
(b)
Figura 103: Gráficos de probabilidade normal da influência dos parâmetros considerados
sobre as variáveis de interesse. (a) pressão e (b) deformação plástica efetiva.
157
A Tabela 12 apresenta as análises de variância (Fo) realizadas a partir da
identificação dos parâmetros e combinações de importância sobre a pressão e a deformação
plástica efetiva por meio dos respectivos gráficos de probabilidade normal. O gráfico de
probabilidade obtido para o caso da pressão revelou que somente 12 efeitos se mostraram
relevantes. Entretanto, Montgomery [77] destaca que os 63 efeitos, incluindo principais e
combinações, devem ser utilizados no cálculo da variância em razão da influência de todos
os efeitos principais sobre a pressão.
Analisando-se estes valores de variância determinados a partir da Equação (173),
pode-se confirmar a relevância dos efeitos principais e suas combinações sobre os modelos
teóricos propostos para estimar a pressão. Ao mesmo tempo, o seu grau de dependência
previamente identificado pelo gráfico de probabilidades com relação à geometria da
matriz, critérios de plasticidade, tribologia e velocidade inicial de prensagem foi reforçado
em função dos distintos valores de variância. A classificação dos parâmetros resultante da
análise de variância destacou em primeiro lugar a forte influência das condições de atrito.
Em relação à geometria da matriz, prevalece a dependência com o ângulo Φ seguida pela
combinação entre os raios de adoçamento. A influência do critério de plasticidade ocupou
o terceiro lugar enquanto o seu acoplamento com as condições de atrito (DE) exibiu
considerável importância ao assumir a quinta posição. Os efeitos da taxa de deformação,
em termos da velocidade inicial V0, apresentaram pequena importância sobre a pressão
quando comparados a parâmetros como o critério de plasticidade e as condições de atrito,
em concordância com a baixa sensibilidade revelada pela liga Al 6061.
Em relação à deformação plástica efetiva, a análise de variância empregou todos
os efeitos geométricos da matriz, ou seja, os efeitos principais A, B e C e suas
combinações, totalizando sete contribuições. Dentre os resultados obtidos, a elevada
variância associada ao ângulo Φ refletiu a forte dependência das soluções propostas frente
às alterações conduzidas sobre a interseção entre os canais, como destacado por
Dumoulin et al. [55] e Eivani et al. [43]. Em seguida, a análise de variância revelou que o
efeito promovido pelos raios de adoçamento foi idêntico embora com significado contrário.
De fato, com base no caso de ausência de adoçamentos, a Tabela 10 mostrou que
introduzindo-se somente um raio de adoçamento interno de 5 mm ocorreu um aumento de
10,73% na previsão de deformação plástica efetiva por passe de prensagem. Entretanto,
uma matriz composta apenas por um raio de adoçamento externo da mesma magnitude
conduz à mesma queda percentual sobre a deformação efetiva após um único passe.
158
Tabela 12 Análise de variância do tipo 26 realizada sobre os modelos propostos.
159
5.3.2 Superfícies de resposta
As Equações (192) e (193) apresentam as expressões que definem as superfícies
de resposta obtidas para a pressão e deformação plástica efetiva, respectivamente. Em
ambos os casos, os respectivos valores do termo ξ0 definido na Equação (174) se referem
às médias entre os valores de pressão e ε resultantes das combinações entre os parâmetros
considerados, conforme mostrado na última linha da Tabela 10. Além disso, os fatores xA
até xF foram calculados de acordo com a Equação (175).
No que se refere à pressão, pode-se observar a presença de ponderações dos
fatores principais xA,..., xF e todas as suas combinações sobre cada termo ξ, com exceção
de ξ0 que está relacionado à combinação (1), a qual não produz efeito. Portanto, as
contribuições associadas às 64 combinações definem a superfície de resposta que
representa os efeitos promovidos pelos parâmetros utilizados na análise fatorial 26 sobre a
prensagem em canais equiangulares.
Em relação à deformação plástica efetiva, foi determinada a expressão para a
superfície de resposta em função dos parâmetros A, B e C e suas combinações. Entretanto,
alguns efeitos exibiram valor nulo e, por esse motivo, foram excluídos da Equação (193).
(192)
(193)
A Figura 104 apresenta a reprodução por parte da superfície de resposta dos
efeitos promovidos sobre a pressão frente às variações geométricas do ferramental,
mantendo-se inalteradas a condição de atrito, o critério de plasticidade e a velocidade de
prensagem. O ângulo de interseção dos canais Φ exerce maior influência com relação à
elevação da pressão do que a combinação entre os raios de adoçamento.
160
Mantendo-se Rext/Rint = 1, quando se aumenta de Φ 90º para 120°, a pressão
diminui de 735 MPa para 518 MPa. Já quando Φ = 90°, a pressão aumenta de cerca de
647 MPa para 735 MPa, ou seja, o ganho de pressão associado ao aumento da razão entre
os raios é menor. Porém, o nível inferior de probabilidade associado ao parâmetro C (Φ)
está relacionado à baixa previsão de pressão quando Φ = 120°, responsável por reduzir a
ação deste parâmetro junto ao respectivo diagrama de probabilidades (vide Figura 103a).
495,000
2400
650,000
2200
2000
Pressão (MPa)
735,000
1800
1600
m = 0,08
κ/σy = 0,58
1400
1200
1000
800
600
400
0
V0 = 1 mm/s
Rext = 5,00 mm
(g
r
au
s)
120
Φ
R /
int R
e xt
1
90
Figura 104: Influência de parâmetros geométricos da matriz sobre a pressão de extrusão.
A Figura 105 apresenta a superfície de resposta dos efeitos combinados entre as
condições de atrito e os parâmetros de configuração geométrica do ferramental. Um
comportamento comum a todos os casos é a elevação de pressão associada ao aumento do
fator de atrito m, ou seja, à medida que a condição de atrito se torna mais severa a carga
necessária à prensagem aumenta. Por outro lado, este conjunto de análises é útil no sentido
de reforçar o fato de que raios de adoçamentos idênticos contribuem para o acréscimo de
pressão independentemente da condição de atrito. Esta observação pode ser identificada
como a primeira evidência de validade da superfície de resposta determinada. Na verdade,
as soluções propostas para o cálculo da pressão são mais sensíveis às variações do ângulo
Φ quando comparadas às alterações sobre os raios de adoçamento.
161
495,000
2400
800,000
2200
1200,000
2000
1600,000
Pressão (MPa)
1800
1880,000
1600
V0 = 1 mm/s
1400
1200
1000
800
600
400
90
Rint/Rext = 0
Rext = 5,00 mm
κ/σy = 0,58
0,16
Φ (g
raus
)
m
0,40
0,32
0,24
0,08
120
(a)
646,000
733,333
2400
1066,667
2200
1400,000
2000
1733,333
1942,000
1600
= 90º
Rext = 5,00 mm
Φ
1400
1200
1000
800
600
400
0
κ/σy = 0,58
V0
= 1 mm/s
0,40
0,32
0,24
0,16
R /R
int
ext
m
Pressão (MPa)
1800
0,08
1
(b)
Figura 105: Efeitos combinados sobre a pressão. (a) Φ e m; (b) raios e m.
Em seguida, a sensibilidade dos modelos de previsão de pressão definida pela
superfície de resposta foi testada em relação às condições de atrito, critério de plasticidade
e taxa de deformação representada pela velocidade de prensagem, como mostra a
Figura 106. Novamente, o atrito desempenhou um papel primário sobre a elevação da
pressão. Ainda, é possível observar um aumento de pressão associado ao acréscimo da
velocidade de prensagem, conforme mostrado na Figura 106a. Este comportamento se
mostrou consistente com as observações reportadas por May et al. [35] referentes a um
aumento de temperatura relacionado ao acréscimo da taxa de deformação na prensagem de
tarugos de alumínio. Portanto, é condizente definir o tempo de deformação do tarugo a
partir do somatório entre as parcelas presentes nas superfícies de entrada e saída e no
interior da zona de deformação, como sugerido nas Equações (113) e (114). A superfície
de resposta reproduz também o acoplamento entre o comportamento plástico e a tribologia
presente no processo PCEA, vide Figura 106b. Nota-se igualmente um aumento na pressão
decorrente do acoplamento entre o fator de atrito e a razão de tensões de escoamento k/σy.
Este foi o segundo indicativo de consistência demonstrado pela superfície de resposta.
162
645,000
2400
2200
2000
1800
1600
1400
1200
1000
800
600
400
1
800,000
1200,000
Pressão (MPa)
1600,000
1910,000
Φ = 90º
Rint/Rext = 0,00
Rext = 5,00 mm
κ/σy = 0,58
0,40
0,32
V
0,24
2
0
0,16
3
(mm
/s)
4
0,08
m
5
(a)
609,000
733,333
2200
1066,667
2000
1400,000
1800
1733,333
Pressão (MPa)
2400
1877,000
1600
1400
1200
1000
800
600
400
0,54
= 90º
V0 = 1 mm/s
Φ
Rint / Rext= 0,00
Rext= 5,00 mm
0,40
0,32
0,24
0,16
0,56
κ/
σ
y
m
0,08
0,58
(b)
Figura 106: Efeitos combinados sobre a pressão. (a) velocidade de prensagem e
tribologia e (b) critério de plasticidade e tribologia.
A terceira verificação está relacionada à dependência com o comportamento
plástico definido pelos critérios de Drucker e von Mises, apresentada na Figura 107. Para
tanto, os efeitos pertinentes às condições de atrito foram minorados assumindo-se a
lubrificação ideal (m = 0,08). A principal importância de se avaliar o comportamento
plástico do material se concentra na idéia de redução da pressão permitida ao se adotar o
critério de Drucker ao invés da expressão proposta por von Mises, em razão do
achatamento da superfície de escoamento que descreve para um material cúbico de faces
centradas, como é o caso da liga Al 6061. Portanto, em concordância com a análise de
variância realizada, o decréscimo de pressão resultante do emprego do critério de Drucker
marcou os casos apreciados na Figura 107. Quanto à combinação de efeitos, as maiores
variações são obtidas a partir de mudanças do ângulo de interseção dos canais. Os raios de
adoçamento dos canais da matriz apresentam uma influência intermediária, ao passo que a
velocidade de prensagem é responsável por menores alterações de pressão. A liga Al 6061
mostra baixa dependência com a taxa de deformação, justificando tal comportamento.
163
2400
2400
467,000
609,000
2200
2200
2000
Pressão (MPa)
647,000
m = 0,08
Rint / Rext= 0,00
Rext= 5,00 mm
1800
1600
1400
1200
1000
800
600
400
0
V0 = 1 mm/s
0,58
Φ
(gr
a
735,000
Pressão (MPa)
2000
1800
1600
1400
1200
1000
800
600
400
90
= 90º
m = 0,08
Rext = 5,00 mm
Φ
V0 = 1 mm/s
0,58
0,56
0,56
us)
0,54
κ
R /R
int
κ/ σ y
ext
1
120
(a)
(b)
609,000
2400
2200
660,000
2000
1800
= 90º
m = 0,08
Rint / Rext= 0,00
Φ
1600
1400
1200
1000
800
600
400
0,54
Rext = 5,00 mm
5
y
1
m
0
0,56
κ/σ
(m
3
2
/s)
4
V
Pressão (MPa)
/σ y
0,54
0,58
(c)
Figura 107: Efeitos combinados sobre a pressão. (a) Φ e κ/σy ; (b) raios e κ/σy e
(c) velocidade inicial e κ/σy.
O quarto e último teste de validade da superfície de resposta busca avaliar a
influência da taxa de deformação, em conjunto com parâmetros geométricos da matriz,
sobre as soluções propostas para o cálculo da pressão. Nesse sentido, a Figura 108
apresenta as análises dos efeitos combinados entre a velocidade de prensagem (V0), o
ângulo Φ e os raios de adoçamento, para lubrificação ideal com o critério de von Mises.
Dentre todos os parâmetros considerados na análise de variância, a velocidade V0 revelou o
menor grau de relevância sobre a pressão devido ao fato de que a liga Al 6061 exibe uma
pequena sensibilidade à taxa de deformação. Por esta razão se observaram as pequenas
variações de pressão mostradas na Figura 108. Mesmo assim, o cálculo da pressão revelou
maior dependência frente às variações de Φ do que em relação aos raios de adoçamento, o
que atesta a consistência da Equação (192) com a variância.
164
496,000
2400
2200
660,000
2000
Pressão (MPa)
1800
m = 0,08
Rint / Rext= 0,00
1600
1400
1200
1000
800
600
400
90
Rext = 5,00 mm
κ / σy = 0,58
5
4
1
120
(m
0
raus
)
V
2
m
/s)
3
Φ (g
(a)
646,000
2400
2200
750,000
2000
Pressão (MPa)
1800
1600
= 90º
m = 0,08
Rext = 5,00 mm
Φ
κ/σ y = 0,58
3
V (mm
0
/ s)
in
t
2
/R
ex
t
1
R
1400
1200
1000
800
600
400
1
0
4
5
(b)
Figura 108: Efeitos combinados sobre a pressão. (a) Φ e V0 e (b) raios e V0.
A Figura 109 apresenta a sensibilidade das deformações plásticas efetivas em
relação à geometria da matriz. Em concordância com a análise de variância realizada,
o ângulo de interseção dos canais Φ exerce considerável influência sobre a pressão em
comparação ao efeito demonstrado pela razão entre os raios de adoçamento. Entretanto,
em razão do decréscimo da deformação plástica efetiva determinado para Φ = 120°,
este parâmetro é classificado como o de mais baixa probabilidade na Figura 103b.
Ademais, o comportamento mostrado pelas previsões de deformação plástica efetiva em
único passe, calculadas a partir das Equações (166) e (167), se mostrou coerente com os
resultados obtidos por Pérez [40], já que são previstos valores máximos de deformação ~
1,15 quando Φ = 90° e 0 ≤ Rext / Rint ≤ 1 mm. De fato, como reportado por este autor, raios
de adoçamentos iguais induzem aos mesmos níveis de deformação observados em ausência
de adoçamento. Portanto, a superfície de resposta se mostrou capaz de reproduzir o
comportamento esperado de dependência com a geometria da matriz.
165
0,600
0,675
0,750
0,825
0,900
0,975
1,050
1,125
1,200
1,1
Def. plástica efetiv
a
1,2
1,0
0,9
0,8
Rext= 5,00 mm
0,7
1
R
Φ (g
in
t
/R
ex
t
0,6
90
raus
)
0
120
Figura 109: Efeitos geométricos da matriz sobre a deformação plástica efetiva.
5.3.3 Perspectivas com base no planejamento fatorial 2k
A partir da aplicação do método fatorial 2k para classificação de parâmetros
geométricos da matriz, critérios de plasticidade, tribologia e condições de processo quanto
às suas relevâncias sobre as soluções analíticas desenvolvidas para os cálculos de carga e
deformações plásticas efetivas oriundas da prensagem em canais equiangulares,
destacaram-se três configurações de matriz que devem ser exploradas com maior
aprofundamento já que podem fornecer observações importantes sobre o comportamento
mecânico do material durante o seu processamento. O primeiro caso é aquele em que se
desconsidera a presença de raios de adoçamento e interseção dos canais da matriz Φ = 90º.
Segundo a literatura, este caso corresponde à condição mais severa de prensagem em que o
modo preponderante de deformação do tarugo é muito próximo ao cisalhamento simples e,
por conseguinte, constitui a configuração de referência para fins de comparação de
resultados [43, 55, 59]. O segundo caso compreende a adoção de um raio de adoçamento
externo com Φ = 90º, visando o decréscimo da força necessária à prensagem. A esta
condição particular cabem as explorações do modo principal de deformação do tarugo e
dos efeitos causados pelo adoçamento sobre a homogeneidade na distribuição das
deformações plásticas efetivas ao longo da superfície deformada do material. O terceiro e
último caso se refere à condição geométrica de raios de adoçamento idênticos sobre as
regiões de interseção dos canais. Além do aumento de carga associado à introdução do raio
de adoçamento interno observado por Yoon et al. [79], cabe analisar se este ferramental
atribui deformação à peça por cisalhamento ou por meio de sucessivos dobramentos.
166
A simulação computacional baseada no método dos elementos finitos representa
uma alternativa bastante interessante para a execução destas análises exploratórias
distintas. Ao mesmo tempo, em coerência com a análise de variância apresentada na
Tabela 12, deve-se considerar a condição de lubrificação ideal para evitar acréscimos e ou
oscilações desnecessários de carga de prensagem. Além disso, pelo fato de que os metais
aqui considerados exibem pequena sensibilidade à taxa de deformação em temperatura
ambiente, apenas a velocidade de prensagem da ordem de 1 mm/s foi adotada, já que o
interesse principal é avaliar o comportamento da amostra. Por fim, a grande maioria dos
programas comerciais baseados no método dos elementos finitos se limita ao critério
isotrópico de von Mises na descrição do comportamento plástico dos materiais. Como
discutido previamente, este critério se mostra conservativo por não permitir a introdução
de parâmetros materiais e por se empregar a hipótese de encruamento isotrópico ao
material em questão. Entretanto, a sua utilização não envolve prejuízos consideráveis sobre
a confiabilidade dos resultados obtidos.
5.4 ANÁLISES NUMÉRICAS DOS EFEITOS DE TAXA DE DEFORMAÇÃO
5.4.1 Análise das grandezas plásticas efetivas resultantes da tração uniaxial
A Figura 110 apresenta as curvas efetivas de tensão e deformação obtidas a partir
da simulação computacional de um teste de tração uniaxial sobre um cubo discretizado por
um único elemento finito com integração reduzida. O objetivo desta análise foi avaliar a
sensibilidade do material modelo quando ajustado pelas leis de encruamento de Hollomon
e Peirce, vide Tabela 3, ao efeito da taxa de deformação sob a forma quase-estática para
posterior adaptação à prensagem em canais equiangulares.
Primeiramente, a análise das curvas obtidas permitiu observar que o limite de
escoamento do material praticamente se manteve em 150MPa ao se elevar a velocidade do
ensaio de 2 mm/s para 8 mm/s. Portanto, a baixa sensibilidade à taxa de deformação do
material modelo empregado nestas análises foi responsável por este comportamento.
167
Em segundo lugar, é possível notar o pequeno acréscimo da tensão efetiva em
razão do aumento da velocidade para 8 mm/s. Este aumento de tensão teve início em
ε ≅ 0,06 e se manteve em caráter exponencial associado à lei de Hollomon até o final
estipulado para a simulação quando ε = 0,35 . O valor máximo de deformação plástica
efetiva indicou também os pontos máximos de tensão em relação às velocidades
consideradas. Para V = 2 mm/s a tensão efetiva alcançou cerca de 396 MPa, ao passo que
aproximadamente 403 MPa foram obtidos quando V = 8 mm/s, revelando um aumento de
apenas 1,8% ao se quadruplicar a velocidade.
A realização deste teste simples evidenciou a possibilidade da simulação numérica
do efeito da taxa de deformação em uma abordagem quase-estática, visto que os resultados
obtidos se mostraram perfeitamente condizentes com o comportamento esperado de
aumento de carga para velocidades maiores. Entretanto, a principal característica do
material frente aos efeitos da taxa de deformação aponta que a inclusão destes efeitos pode
ser explorada a partir de um único valor de velocidade.
500
Tensão efetiva (MPa)
450
400
350
300
250
200
150
100
50
0
Tração uniaxial, V = 2 mm/s
Tração uniaxial, V = 8 mm/s
0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40
Def. plástica efetiva
Figura 110: Efeito da velocidade de tração sobre o material modelo.
168
5.4.2 Simulação da técnica PCEA
5.4.2.1 Previsões de carga de prensagem
A Figura 111 apresenta as curvas de força de prensagem em função do
deslocamento obtidas a partir da simulação por elementos finitos, para as geometrias
assinaladas pelo método fatorial 2k, da prensagem de tarugos com comportamento plástico
definido ora somente pela lei de Hollomon, ou seja, desconsiderando-se o efeito da taxa de
deformação ora pela combinação entre as leis de Hollomon e Peirce, sendo a última
responsável pela sensibilidade à taxa de deformação. considerando o efeito da taxa de
deformação. Os arranjos de matriz considerados nas simulações incluem a ausência de
adoçamentos (β = 0º), adoçamento externo (β = 38º) e raios de adoçamento idênticos
(β = 0º). Ainda, assumiu-se a condição de lubrificação ideal com µ = 0,05, ou fator de
atrito m = 0,08, entre o tarugo e a matriz. O critério de escoamento utilizado foi a descrição
isotrópica de von Mises.
100
100
Φ = 90º
µ = 0,05
80
a
Força (kN)
70
60
b
c"
c
c'
b'
50
40
0 o
0
d"
e"
d'
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
45
60
50
40
0 O
0
E"
D
D'
B"
A'
30
Rint , Rext : 0 mm e 5 mm
D"
C'
B'
Sem adoçamentos,
β = 0º
Adoçamento externo, β = 38º
Adoçamentos idênticos, β = 0º
10
50
C"
C
20
Sem adoçamentos,
β = 0º
Adoçamento externo, β = 38º
Adoçamentos idênticos, β = 0º
a"
AB
70
d
20
10
80
Rint , Rext : 0 mm e 5 mm
b"
a'
30
Φ = 90º
µ = 0,05
90
Força (kN)
90
A"
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
45
50
Figura 111: Previsões numéricas de força de prensagem para arranjos distintos de matriz.
(a) material modelo sem efeito de taxa e (b) material modelo com efeito de taxa.
De uma forma geral, pela contribuição aditiva da lei de Peirce definida na
Equação (115), pode-se notar um pequeno acréscimo nas previsões de carga de prensagem
(Figura 111b) quando se compara ao material cujo comportamento plástico descarta o
efeito da taxa de deformação, ou seja, o encruamento envolve apenas a lei de Hollomon,
conforme apresentado na Figura 111a.
169
Na ausência de adoçamentos, observa-se que as curvas de carga obtidas se
dividem em três partes distintas. A primeira caracteriza-se por um rápido aumento de carga
entre os pontos o e a da Figura 111a e O e A da Figura 111b após cerca de 5 mm de
deslocamento, onde os pontos a e A correspondem às previsões máximas de carga
próximas a 70 kN e 72 kN, respectivamente. A segunda parte está associada ao
dobramento do tarugo na região externa de interseção dos canais da matriz. A progressiva
queda de carga que se estende até ambos os pontos c e C, respectivamente mostrados nas
Figuras 111a e 111b está diretamente relacionada ao desenvolvimento das regiões de perda
de contato entre o tarugo e as partes inferiores das matrizes. A terceira parte compreende as
regiões entre os pontos c e d e C e D nas quais ocorreram uma contínua e acentuada queda
de carga. Este fato se deve à combinação entre os efeitos de descarregamento elástico e
saturação das deformações plásticas efetivas.
A inclusão do adoçamento externo (em vermelho nas Figuras 111a e 111b)
evidenciou também a presença de três estágios distintos ao longo das curvas de carga. O
primeiro estágio mostrou uma considerável elevação de carga ao longo das regiões
ob’ e OB’ em conseqüência dos efeitos combinados entre as trajetórias oa’ e OA’ e a’b’ e
A’B’. As regiões oa’ e OA’ refletem a adaptação da base dos tarugos ao adoçamento
externo a partir dos seus forjamentos após cerca de 5 mm. O forjamento dos materiais
causou o acréscimo de carga para ~ 20 kN (ponto a’) e 22 kN (ponto A’). As regiões a’b’ e
A’B’ mostraram a combinação entre os modos de deformação por forjamento e
compressão plana devido ao contato entre as bases encruadas dos tarugos e as porções
inferiores dos canais de saída das matrizes. O grau de severidade deste processo
combinado de deformação foi tal que promoveu acréscimos da força de 20 kN e 22 kN
para cerca de 45 kN após somente 2 mm de deslocamento do tarugo para ambas as curvas
de carga apresentadas na Figura 111.
O segundo estágio, delimitado por b’ e c’ (Figura 111a) e B’ e C’ (Figura 111b),
apontou um suave aumento de carga de 45 kN (pontos b’ e B’) para ~ 51 kN sobre c’ e C’
após cerca de 10 mm. Este acréscimo de carga está relacionado a um dobramento similar
ao observado durante a prensagem da liga Al 6070 que originou uma pequena região de
solicitação sobre a ferramenta junto à região superior do canal de saída. Sendo assim, o
aumento de carga diz respeito às propriedades mecânicas superiores do material modelo
quando exposto a um determinado nível de deformação plástica. Logo, a coerência com o
processo de deformação implica em se considerar a carga máxima sobre os pontos b’ e B’.
170
O terceiro estágio, delimitado entre c’ e d’ (Figura 111a) e C’ e D’ (Figura 111b),
apontou a contínua queda de carga até 40 mm de deslocamento do tarugo, a qual está
associada à saturação das deformações plásticas efetivas, como será abordado adiante.
A curva de carga originada após a prensagem dos tarugos no interior de matrizes
compostas por raios de adoçamento idênticos (em azul, Figura 111) mostrou quatro fases
diferentes. Todavia, os aumentos sucessivos de carga na forma de degraus entre os pontos
b” e c” (Figura 111a) e B” e C” (Figura 111b) se constituem em uma forte evidência de
que o modo principal de deformação plástica do material passou a ser uma combinação
entre o dobramento e o cisalhamento simples. O trabalho de Rosochowski et al. [78]
apresenta uma relação crítica entre a largura e o comprimento dos canais para dois passes
consecutivos, em condições de cisalhamento. Entretanto, a forma da curva em azul
mostrada na Figura 111 destaca que mesmo durante o primeiro passe a presença de um raio
interno igual ao externo altera a condição que controla a deformação do material.
A primeira fase compreende a região delimitada pelos pontos o e b” da
Figura 111a e O e B” da Figura 111b. As regiões oa” e OA” mostraram um aumento de
carga que atingiu 12 kN após 4 mm sobre ambos os pontos a” e A” em razão do forjamento
dos materiais, como ilustrado na Figura 112a. Por outro lado, nas regiões a”b” e A”B” os
tarugos se deformaram em condições combinadas de forjamento e deformação plana ao
atingirem a base das matrizes, conforme apresentado na Figura 112b. Dessa forma, os
respectivos valores de força sobre os pontos b” e B” foram 43,1 kN e 43,6 kN após cerca
de 8 mm de deslocamento e este aumento em relação às previsões sobre a” e A” reflete a
severidade geométrica imposta aos tarugos pela matrizes.
A segunda fase foi delimitada pelos pontos b” e c” (Figura 111a) e
B” e C” (Figura 111b) e apontou sobre estes últimos pontos os respectivos valores
numéricos máximos considerados para estas simulações, ou seja, 56 kN e 57 kN. Estas
regiões permitiram observar um traço marcante relacionado à presença de raios de
adoçamento idênticos, ou seja, após cerca de 10 mm nota-se que o favorecimento à
elevação de carga se tornou mais evidente, de modo para se atingir os máximos de força
(em c” e C”, após 16 mm) foram necessários apenas 6 mm. Este rápido aumento de carga
se deve ao fato de que após 10 mm teve início o contato entre o tarugo e a porção superior
dos canais de saída das matrizes, conforme destacado em vermelho na Figura 112c.
171
Estas interfaces de contato atuaram como uma espécie de contrapressão ao movimento
preferencial das peças já que as matrizes, por possuírem propriedades mecânicas superiores
promoveram o preenchimento dos canais por parte dos tarugos ao serem pressionadas
pelos mesmos durante a sua passagem em direção à saída. Em outras palavras, este efeito
de preenchimento dos canais foi o responsável pela deformação combinada entre
dobramento e cisalhamento do tarugo, originando a forma quase-sigmoidal acompanhada
pelo aumento de carga das regiões b”c” e B”C” mostradas na Figura 111.
A terceira fase, compreendida entre os pontos c” e d” e C” e D”, revelou em
menor grau o efeito de contrapressão que resultou em uma pequena elevação de carga
sobre os pontos d” e D” (60 kN) em comparação aos pontos c” e C”. Conforme mostrado
na Figura 112d, o encruamento do material causa um leve acréscimo de carga e impede
que o mesmo se modele perfeitamente à matriz, originando pequenas zonas de
descolamento junto à região do raio de adoçamento externo.
A quarta fase, delimitada por d” e e” (Figura 111a) e D” e E” (Figura 111b),
mostra a saturação das deformações plásticas efetivas e o descarregamento elástico que
conduziram à queda da carga para 56 kN (em e” e E”), após 40 mm de deslocamento.
Contato com a base da matriz
(a)
(b)
(c)
(d)
Figura 112: Estágios de deformação do tarugo em matrizes com adoçamentos iguais.
(a) regiões de forjamento e descolamento, após 4 mm; (b) descolamento e contato com a
base da matriz, após 8 mm; (c) contato com a parte superior do canal de saída, após
16 mm e (d) preenchimento quase completo dos canais pelo tarugo, após 25 mm.
172
A Figura 113 compara as previsões numéricas de carga obtidas para o material
modelo com comportamento plástico descrito de forma distinta pela lei de Hollomon e pela
sua combinação à parcela de taxa de deformação definida pelo modelo de Peirce,
deformado no interior de matrizes com diferentes geometrias (Φ = 90º), adotando a
lubrificação ideal. Pode-se notar que em todos os casos geométricos da matriz
considerados, a inclusão do modelo de Peirce na descrição do comportamento plástico do
material conduziu a um pequeno aumento da carga de prensagem, o que concorda
plenamente com a contribuição aditiva desta lei à Equação (115). Entretanto, cabe ressaltar
que a pequena elevação de força de prensagem relacionada ao efeito da taxa de deformação
se deve à baixa dependência do material modelo a parâmetros de viscoplasticidade
traduzida pelo valor de 0,05 atribuído ao expoente s de sensibilidade à taxa de deformação.
100
100
Material modelo, sem efeito de taxa
Material modelo, com efeito de taxa
90
80
70
Força (kN)
Força (kN)
80
Material modelo, sem efeito de taxa
Material modelo, com efeito de taxa
90
60
50
40
30
70
60
50
40
30
20
Φ = 90º
µ = 0,05
10
0
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
45
Rint = 0,00 mm
10
Rint , Rext : 0,00 mm
0
Φ = 90º
µ = 0,05
20
Rext = 5,00 mm
0
50
0
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
(a)
45
50
(b)
100
Material modelo, sem efeito de taxa
Material modelo, com efeito de taxa
90
Força (kN)
80
70
60
50
40
30
20
Φ = 90º
µ = 0,05
10
Rint ; Rext = 5,00 mm
0
0
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
45
50
(c)
Figura 113: Comparação entre as curvas de carga do material modelo com e sem o efeito
da taxa de deformação. (a) sem raios de adoçamento; (b) raio de adoçamento externo e
(c) raios de adoçamento iguais.
173
A Figura 114 compara as previsões numéricas de tensão efetiva média oriundas
do critério de von Mises associadas às mesmas condições geométricas da matriz e de atrito
utilizadas na determinação das curvas de carga de prensagem apresentadas na Figura 113.
De fato, a inclusão do efeito viscoplástico ao comportamento do material modelo causou o
aumento da tensão efetiva, principalmente após cerca de 10 mm de deslocamento onde o
escoamento plástico do tarugo se mostra intenso, quando comparado ao material com
comportamento plástico governado somente pela lei de Hollomon, o que justifica o
aumento da carga de prensagem mostrado na Figura 113. O efeito de taxa de deformação
representado pela lei de Peirce promove a elevação da tensão de escoamento do material e
induz estados de tensão superiores que são traduzidos de forma equivalente pela tensão
efetiva, ou seja, aumenta a sua resistência ao escoamento plástico embora de forma suave
já que o material modelo apresenta baixa sensibilidade aos efeitos de viscoplasticidade.
500
Φ = 90º
µ = 0,05
450
400
Tensão efetiva média (MPa)
Tensão efetiva média (MPa)
500
Rint , Rext : 0,00 mm
350
300
250
200
150
100
Material modelo, sem efeito de taxa
Material modelo, com efeito de taxa
50
0
0
5
10
15
20
25
30
35
40
45
Φ = 90º
µ = 0,05
450
400
Rint = 0,00 mm
350
Rext = 5,00 mm
300
250
200
150
100
Material modelo, sem efeito de taxa
Material modelo, com efeito de taxa
50
0
50
0
Deslocamento do tarugo (mm)
5
10
15
20
25
30
35
40
45
50
Deslocamento do tarugo (mm)
(a)
(b)
Tensão efetiva média (MPa)
500
450
400
Φ = 90º
µ = 0,05
Rint , Rext : 5,00 mm
350
300
250
200
150
100
Material modelo, sem efeito de taxa
Material modelo, com efeito de taxa
50
0
0
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
45
50
(c)
Figura 114: Comparação entre as curvas de tensão efetiva média do material modelo
com e sem o efeito da taxa de deformação. (a) sem raios de adoçamento; (b) raio de
adoçamento externo e (c) raios de adoçamento iguais.
174
5.4.2.2 Previsões de deformação plástica efetiva
A Figura 115 mostra as curvas deformação plástica efetiva x deslocamento do
tarugo, obtidas por meio de simulação computacional, referentes à prensagem do material
modelo independente da taxa de deformação (Figura 115a) e sensível aos efeitos
viscoplásticos (Figura 115b) através de configurações geométricas distintas para a matriz.
Cabe ressaltar que os valores apresentados se referem à média entre os resultados obtidos
para um bloco de elementos finitos representativos do tarugo destinado a esta análise.
A matriz desprovida de raios de adoçamento forneceu uma previsão máxima em
torno de 1,18 obtida após 22 mm para ambos as descrições de encruamento. Este resultado
concorda com as previsões numéricas obtidas por Yoon et al. [79]. Além disso, a
proximidade entre tais resultados confirma a idéia de Iwahashi et al. [37] na qual as
deformações experimentadas pelo material têm forte dependência com a geometria da
matriz, o que atesta a validade do modelamento numérico proposto para materiais com ou
sem sensibilidade à taxa de deformação.
1,4
Φ = 90º
εmax = 1,20
1,2
Def. plástica efetiva média
Def. plástica efetiva média
1,4
1,0
0,8
0,6
0,4
0,2
Sem adoçamentos
Adoçamento externo
Adoçamentos idênticos
0,0
0
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
(a)
45
Φ = 90º
εmax = 1,20
1,2
1,0
0,8
0,6
0,4
0,2
Sem adoçamentos
Adoçamento externo
Adoçamentos idênticos
0,0
50
0
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
45
50
(b)
Figura 115: Previsões de deformação plástica efetiva resultantes de geometrias distintas
para a matriz. (a) sem efeitos viscoplásticos e (b) com efeitos viscoplásticos.
A introdução do adoçamento externo conduziu à queda de deformações plásticas
efetivas em razão da maior facilidade de escoamento do material. Nesse sentido, os valores
máximos observados foram de 1,14 após cerca de 30 mm de deslocamento da peça. Além
de promover a diminuição de ε , o adoçamento externo causou também o deslocamento da
curva para a esquerda, em comparação ao caso anterior. A presença de adoçamento externo
aumentou a distância a ser percorrida pela peça para atingir a porção inferior da matriz.
175
Em relação à validade destes modelos numéricos, Dumoulin et al. [55] obteve previsões
numéricas próximas a 1,0 considerando tal geometria de matriz e considerando materiais
perfeitamente plásticos e distintas condições de atrito. Previsões numéricas de ε próximas
à unidade foram também encontradas por Alkorta et al. [38] considerando valores distintos
para o expoente de encruamento do material e em ausência de atrito, o que reforça a
dependência das deformações plásticas efetivas somente com a geometria da matriz.
Os ferramentais constituídos por raios de adoçamento iguais forneceu previsões
máximas de 1,18, ou seja, idênticas ao caso das matrizes sem raios de adoçamento. A
saturação, com ε ≅ 1,18 , ocorreu após cerca de 30 mm de deslocamento. O aumento dos
deslocamentos necessários à saturação das deformações plásticas efetivas está relacionado
também à maior distância percorrida pelo tarugo ao ser introduzido o raio de adoçamento
interno. A forma exibida pela curva de carga, caracterizada pela presença de ondulações, é
um indicativo direto da influência combinada entre as componentes de cisalhamento e,
possivelmente, da componente horizontal associada diretamente ao efeito da contrapressão.
No que diz respeito à validade destes modelos numéricos, Pérez [40] realizou a
simulação da prensagem de materiais perfeitamente plásticos a partir deste arranjo para a
ferramenta, variando-se as condições de atrito. O máximo valor encontrado pelo autor para
todas as condições de atrito empregadas foi de 0,8. Sendo assim, pela concordância entre
os resultados obtidos no presente trabalho e a literatura, pode-se verificar a validade do
modelamento proposto para materiais que exibem ou não a dependência à taxa de
deformação já que a geometria da matriz exerce importância fundamental sobre as
previsões de ε . Vale destacar que as previsões obtidas no presente trabalho se referem a
valores médios associados a um conjunto de elementos que buscam representar o
comportamento da peça.
A Figura 116 apresenta a comparação entre a distribuição nodal das deformações
plásticas efetivas ao longo das superfícies deformadas dos tarugos independentes
(Figuras 116a e 116c) e sensíveis (Figuras 116b e 116d) à taxa de deformação por meio das
matrizes consideradas. De uma forma geral, a inclusão destes efeitos a partir da lei de
Peirce, por elevar a tensão de escoamento plástico do material, permite níveis maiores de
deformação plástica efetiva em comparação à descrição do encruamento somente pela lei
de Hollomon. Em ausência de adoçamentos, as extensas regiões em verde oliva denotam as
zonas uniformes de deformações efetivas.
176
As pequenas perturbações nas cores vermelha, amarela e verde clara se devem à
passagem da base dos tarugos em direção aos canais de saída das matrizes. Já a introdução
do adoçamento externo, vide Figuras 116c e 116d, promove uma redução na altura destas
zonas uniformes acompanhada por uma redução das deformações efetivas. Neste caso,
consideram-se como regiões uniformes de deformações as porções com coloração amarela.
Mesmo com o decréscimo na quantidade de deformações atribuídas aos tarugos, esta
configuração se mostra interessante em virtude da queda promovida sobre a carga,
conforme apresentado na Figura 115.
As matrizes com raios de adoçamento iguais fornecem uma considerável redução
das zonas uniformes de deformações plásticas efetivas, também de cor amarela e refletem
os prejuízos causados por esta configuração à qualidade final do material deformado.
(a)
(b)
(c)
(d)
(e)
(f)
Figura 116: Iso-contornos de deformação plástica efetiva ao longo do tarugo deformado
para diferentes arranjos geométricos de matriz. (a) ausência de adoçamentos-sem taxa;
(b) ausência de adoçamentos com taxa; (c) adoçamento externo-sem taxa;
(d) adoçamento externo-com taxa; (e) adoçamentos idênticos-sem taxa e
(f) adoçamentos idênticos-com taxa.
177
Os aspectos observados durante a análise da Figura 116 indicam a necessidade de
se avaliar o grau de homogeneidade das deformações plásticas efetivas impostas ao
material quando processado no interior de matrizes distintas.
Para melhor explorar os resultados, as superfícies deformadas dos tarugos
compostos ora pelo material modelo independente dos efeitos viscoplásticos ora pelo
material modelo sensível à taxa de deformação, relativas a cada uma das matrizes
consideradas, foram divididas em quatro partes ao longo das direções vertical e horizontal,
seguindo o procedimento descrito em 3.2 MÉTODOS. Em seguida, foram obtidas as
componentes de deformação plástica relativas à condição de deformação plana para cada
direção. Esta exploração permite avaliar, de forma simultânea, a homogeneidade na
distribuição da deformação plástica efetiva e o modo principal de deformação.
A Figura 117 mostra a distribuição das componentes de deformação plástica nas
direções vertical e horizontal ao longo da superfície deformada dos tarugos obtida para o
caso de matrizes desprovidas de raios de adoçamento. Ao longo da direção vertical todas
as componentes exibiram um pequeno aumento inicial relacionado ao atrito do tarugo com
a porção superior da matriz. Em seguida, observa-se a estabilização destas componentes,
indicando a porção média da peça deformada por cisalhamento simples, ou seja, a zona
uniforme de deformações. Na Figuras 117e e 117f as regiões em verde oliva denotam a
zona homogênea de deformações efetivas ao longo das quais os elementos finitos exibem
distorções iguais que caracterizam a preponderância do cisalhamento simples. Após estas
regiões, percebe-se uma queda contínua sobre as componentes de deformação à medida
que se alcança a porção inferior dos tarugos em contato com a base dos canais de saída das
matrizes. Esta diminuição continuada reflete a quase ausência de plasticidade sobre esta
região quando comparada à superfície média da peça e reforça a idéia de Eivani et al. [43]
de que ao atravessar a região de interseção dos canais o material se movimenta como um
corpo rígido, ou seja, não experimenta níveis consideráveis de deformação plástica.
A distribuição de componentes de deformação plástica ao longo da direção
horizontal (Figuras 117c e 117d) comprova a afirmação anterior, uma vez que se verifica
uma relativa estabilização destas componentes. Além disso, esta distribuição praticamente
inalterada revela um considerável grau de homogeneidade de deformação a que os
materiais são expostos quando processados em matrizes sem raios de adoçamento. Este
resultado, reportado igualmente por Kim et al. [50], indica que materiais com média a alta
capacidade de encruamento apresentam uma elevada homogeneidade na distribuição de ε .
178
Finalmente, os valores superiores mostrados pela componente εxy para ambos os
materiais em comparação às demais componentes e a sua proximidade com a deformação
plástica efetiva nas direções consideradas garante o cisalhamento simples como modo
dominante de deformação para esta configuração de matriz a partir da correção igual a
1/√3 oriunda do critério de von Mises. Ao mesmo tempo pode-se confirmar a consistência
destes modelos numéricos com relação à inclusão dos efeitos da taxa de deformação.
2,0
1,5
1,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
5
10
15
20
25
1,0
0,5
0,0
-0,5
-1,0
-1,5
30
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
5
10
15
20
25
Distância vertical média (mm)
(a)
30
(b)
2,0
Φ = 90º
β = 0º
µ = 0,05
1,5
1,0
0,5
0,0
-0,5
-1,0
εx ;
-1,5
-2,0
Φ = 90º
β = 0º
µ = 0,05
1,5
-2,0
Distância vertical média (mm)
2,0
Deformação plástica média
Deformação plástica média
Φ = 90º
β = 0º
µ = 0,05
Deformação plástica média
Deformação plástica média
2,0
εy ;
ε1 ;
0
5
10
εz ;
ε2 ;
15
20
εxy
ε3 ;
25
30
εef
35
40
(c)
1,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
45
Distância horizontal média (mm)
50
Φ = 90º
β = 0º
µ = 0,05
1,5
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
10
20
30
40
50
60
Distância horizontal média (mm)
(d)
(e)
(f)
Figura 117: Componentes de deformação plástica sobre a superfície do tarugo deformado
pela matriz sem adoçamentos. (a) direção vertical-sem taxa; (b) direção verticalcom taxa; (c) direção horizontal-sem taxa; (d) direção horizontal-com taxa; (e) previsões
numéricas de ε -sem taxa e (f) previsões numéricas de ε -sem taxa.
179
A Figura 118 apresenta a distribuição das componentes de deformação observada
sobre a superfície de tarugos constituídos pelo material modelo com comportamento
plástico independente (Figuras 118a e 118c) ou sensível (Figuras 118b e 118d) aos efeitos
viscoplásticos, processados através da matriz com adoçamento externo. Nestes casos, os
comportamentos observados ao longo da direção vertical são bastante similares ao caso
anterior, ou seja, o atrito entre as peças e as partes superiores dos canais de saída das
matrizes conduz a um leve acréscimo sobre as componentes de deformação. Em seguida, a
estabilização destas revelou uma considerável homogeneidade sobre as superfícies médias
dos tarugos em razão do cisalhamento simples uniforme atribuído aos materiais mostrados
nas Figuras 118 e e 118f em coloração amarela. Os subseqüentes decréscimos apontam o
movimento de corpo rígido presente ao longo das interfaces de contato entre as peças e as
regiões inferiores dos ferramentais. A direção horizontal indica, de forma análoga ao caso
prévio, a tendência comum à estabilidade em relação às componentes de deformação
plástica. Ainda, a proximidade entre as componentes εxy e ε ao longo das direções vertical
e horizontal confirma a preponderância do cisalhamento simples sobre os demais modos de
deformação apresentados na Figura 118. Portanto, mesmo com a adição do adoçamento
externo o processo de deformação dos materiais continuou sendo a prensagem em canais
equiangulares. Dessa forma, podem-se explicar as formas similares apresentadas na
Figura 115 para as curvas deformação plástica efetiva x deslocamento referentes à
prensagem de tarugos em matrizes sem adoçamento ou com raios de adoçamento externo.
Segundo Dumoulin et al. [55], a adição do raio de adoçamento externo contribui
fortemente para o aumento da homogeneidade na distribuição das deformações plásticas
efetivas ao longo da superfície média deformada da peça. Aliando-se esta observação ao
fato de que não houve uma notável diminuição sobre as previsões de ε em relação ao
presente caso ao ser comparado à ausência de adoçamentos pode-se confirmar os
benefícios alcançados sobre a qualidade final do material ao se introduzir um raio de
adoçamento externo de forma que o ângulo β que o delimita seja igual a 38º.
Em relação ao comportamento plástico do material modelo, cabe ressaltar que a
deformação plástica efetiva apresenta uma dependência quase exclusiva com a geometria
da matriz, ou seja, a inclusão dos efeitos de viscoplasticidade praticamente não alterou as
previsões numéricas das componentes de deformação apresentadas na Figura 118,
seguindo a mesma tendência do caso prévio em que se desconsiderou a presença dos raios.
180
2,0
Φ = 90º
β = 38º
µ = 0,05
1,5
1,0
Deformação plástica média
Deformação plástica média
2,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
5
10
15
20
25
1,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
30
Φ = 90º
β = 38º
µ = 0,05
1,5
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
5
10
(a)
25
30
2,0
Φ = 90º
β = 38º
µ = 0,05
1,5
1,0
Deformação plástica média
Deformação plástica média
20
(b)
2,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
15
Distância vertical média (mm)
Distância vertical média (mm)
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
10
20
30
40
50
Distância horizontal média (mm)
1,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
60
Φ = 90º
β = 38º
µ = 0,05
1,5
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
10
20
30
40
50
Distância horizontal média (mm)
(c)
(d)
(e)
(f)
60
Figura 118: Componentes de deformação plástica sobre a superfície do tarugo deformado
pela matriz com raio de adoçamento externo. (a) direção vertical-sem taxa; (b) direção
vertical- com taxa; (c) direção horizontal-sem taxa; (d) direção horizontal-com taxa; (e)
previsões numéricas de ε -sem taxa e (f) previsões numéricas de ε -sem taxa.
181
A Figura 119 apresenta a distribuição das componentes de deformação plástica ao
longo da superfície deformada de tarugos com comportamento plástico distinto ora
definido somente pela lei de Hollomon (independente de efeitos viscoplásticos) ora
descrito segundo a combinação entre as leis de Hollomon e Peirce sendo esta última
responsável por incluir a sensibilidade à taxa de deformação, obtidas após a prensagem
através de matrizes dotadas de raios de adoçamento idênticos. Para esta configuração, a
direção vertical mostra um relevante acréscimo da componente εxy nas regiões próximas às
porções superiores dos tarugos. Este comportamento é a reação da matriz frente à
solicitação exercida pelas peças quando alcançam sua porção inferior e dá início ao
escoamento plástico em direção aos canais de saída. Em outras palavras, é o efeito da
contrapressão discutido anteriormente em relação às previsões de carga oriundas desta
configuração da matriz. A tendência à heterogeneidade ao longo das porções médias dos
tarugos, refletida pelo caráter oscilatório da componente de cisalhamento em comparação
aos casos anteriores se deve à considerável diminuição da zona uniforme de deformação
plástica efetiva atribuída por esta matriz, conforme apresentado nas Figuras 119e e 119f.
Em uma primeira análise, o fato de que as previsões de cisalhamento se
mostraram próximas às de deformação plástica efetiva pode indicar a conformação de
ambos os materiais governada somente pelo cisalhamento simples. Todavia, ao se avaliar a
distribuição das componentes de deformação plástica ao longo da direção horizontal,
verificou-se a diminuição de εxy a níveis inferiores aos de ε e até mesmo da componente x.
As Figuras 119a e 119b mostram o decréscimo das componentes plásticas cisalhante e
efetiva para níveis inferiores a 0,75 até então não observado, o que causou a aproximação
entre tais componentes e a horizontal εx. Esta aproximação confirma o fato de que os
materiais são deformados pela ação conjunta entre cisalhamento e dobramento. O efeito
promovido por εx é justamente a contrapressão exercida pela matriz sobre os tarugos
quando estes atingem as regiões superiores dos canais de saída das matrizes, o que resulta
nos dobramentos sucessivos identificados na respectiva curva de carga x deslocamento
apresentada na Figura 111.
Por fim, verifica-se que as previsões numéricas das componentes de deformação
plástica praticamente independem dos efeitos viscoplásticos e são fortemente afetadas pela
geometria do ferramental quando comparadas aos casos analisados anteriormente de
ausência de raios de adoçamento ou considerando-se apenas o raio de adoçamento externo.
182
2,0
Φ = 90º
β = 0º
µ = 0,05
1,5
1,0
Deformação plástica média
Deformação plástica média
2,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
5
10
15
20
25
Distância vertical média (mm)
Φ = 90º
β = 0º
µ = 0,05
1,5
1,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
30
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
5
10
(a)
25
30
2,0
Φ = 90º
β = 0º
µ = 0,05
1,5
1,0
Deformação plástica média
Deformação plástica média
20
(b)
2,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
15
Distância vertical média (mm)
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
10
20
30
40
50
Distância horizontal média (mm)
1,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
60
Φ = 90º
β = 0º
µ = 0,05
1,5
0
εx ;
εy ;
εz ;
εxy
ε1 ;
ε2 ;
ε3 ;
εef
10
20
30
40
50
60
Distância horizontal média (mm)
(c)
(d)
(e)
(f)
Figura 119: Componentes de deformação plástica sobre a superfície do tarugo deformado
pela matriz com raios de adoçamento iguais. (a) direção vertical-sem taxa; (b) direção
vertical- com taxa; (c) direção horizontal-sem taxa; (d) direção horizontal-com taxa; (e)
previsões numéricas de ε -sem taxa e (f) previsões numéricas de ε -sem taxa.
183
5.4.2.3 Validação das soluções analíticas com efeito de taxa de deformação
A Figura 120 compara as previsões analíticas e numéricas de força de prensagem
oriundas dos modelos desenvolvidos no presente trabalho, considerando materiais modelo
dependentes ou não de viscoplasticidade, para os casos geométricos da matriz na ausência
de raios de adoçamento e somente o raio de adoçamento externo, com o intuito de analisar
a influência da taxa de deformação e validar as soluções teóricas propostas. Para tanto, os
previsões foram obtidos a partir da prensagem dos materiais modelo assumindo-se a
condição de lubrificação ideal associada ao critério de plasticidade isotrópico de
von Mises e assumindo-se Φ = 90º em todos os casos.
De forma geral, a inclusão do efeito viscoplástico descrito pela lei de Peirce ao
encruamento do material governado ainda pela lei de Hollomon revelou um pequeno
acréscimo da carga de prensagem tanto nas previsões teóricas calculadas com o método do
limite superior como nos resultados numéricos obtidos via o método dos elementos finitos.
Na verdade, a lei de Peirce tem o aspecto aditivo definido na Equação (115) o que tende a
aumentar suavemente as previsões teóricas e numéricas da tensão de escoamento do
material já que sua sensibilidade à taxa de deformação traduzida pelo expoente s, em
temperatura ambiente, é pequena.
Em ausência de adoçamentos (Figura 120a), pode-se comprovar tanto o caráter
conservativo associado ao método do limite superior, em relação aos resultados numéricos
como também a influência do efeito viscoplástico na elevação da carga de prensagem.
Nesse sentido, pode-se comprovar o correto modelamento teórico proposto no presente
trabalho que estendeu as soluções analíticas desenvolvidas por Pérez et al. [45] a materiais
que exibem encruamento dependente dos efeitos de taxa de deformação.
A adição do adoçamento externo promoveu a queda das previsões analíticas e
numéricas de força, conforme apresentado na Figura 120b. Observa-se que, embora
mantendo seu caráter conservativo, o modelo teórico revelou menor sensibilidade ao efeito
do raio de adoçamento do que o modelo numérico já que apresentou uma diminuição de
14 % para o material independente da taxa de deformação e 16% com a inclusão da
viscoplasticidade, em relação à ausência de adoçamentos, ao passo que a solução por
elementos finitos originou decréscimos respectivos de 37 % e 38%. A hipótese adotada na
extensão dos modelos propostos por Pérez et al. [45] de que o tarugo ocupa perfeitamente
os canais da matriz justifica este comportamento em razão do aparecimento de zonas de
perda de contato com a matriz que causam alívio de carga.
184
200
180
Força ( kN)
160
140
Φ = 90º
µ = 0,05; m = 0,08
MLS - sem taxa
MLS - com taxa
MEF - sem taxa
MEF - com taxa
Rint, Rext = 0,00 mm
120
100
91,70
91,81
80
71,00
72,11
60
40
20
0
0
β (graus)
(a)
200
180
Força ( kN)
160
140
MLS - sem taxa
MLS - com taxa
MEF - sem taxa
MEF - com taxa
Φ = 90º
µ = 0,05; m = 0,08
Rint = 0,00 mm
Rext = 5,00 mm
120
100
80
78,45
78,50
60
44,50
40
45,00
20
0
38
β (graus)
(b)
Figura 120: Comparação entre previsões teóricas e numéricas de força.
(a) sem raios de adoçamento; (b) raio de adoçamento externo.
A matriz com raios de adoçamentos idênticos causou aumentos de carga tanto
para as soluções analíticas como para os modelos numéricos discretizado por elementos
finitos, conforme apresentado na Figura 121. Segundo Yoon et al. [79] este
comportamento é o resultado da adição do raio de adoçamento interno. Todavia, o aumento
de carga previsto pelo modelo teórico foi tal que ambos os resultados associados ao
comportamento plástico do material modelo se mostraram apenas cerca de 1,4% menores
que aqueles oriundos da geometria desprovida de raios de adoçamento. Por outro lado, os
resultados numéricos indicaram que a presença do raio de adoçamento interno induziu a
respectivos aumentos de 28 % e 27 % na carga quando se compara à Figura 120b. Em
relação à ausência de adoçamentos (Figura 120a), houve decréscimos de 20 % e 21 %.
185
200
180
Força ( kN)
160
140
Φ = 90º
µ = 0,05; m = 0,08
MLS - sem taxa
MLS - com taxa
MEF - sem taxa
MEF - com taxa
Rint, Rext = 5,00 mm
120
100
90,44
90,50
80
57,00
60
57,00
40
20
0
0
β (graus)
Figura 121: Comparação entre previsões teóricas e numéricas de força oriundas da
matriz com raios de adoçamento idênticos.
A Figura 122 apresenta a comparação entre as previsões analíticas e numéricas de
deformação plástica efetiva relativas às configurações consideradas para a matriz. A
proximidade entre os resultados teóricos calculados e numéricos obtidos via o método dos
elementos finitos confirma a validade dos modelos teóricos propostos em que as condições
de atrito e a taxa de deformação não exercem influência sobre ε , ao contrário da sua forte
dependência com a geometria da matriz. Além disso, o cisalhamento prevaleceu como
modo de deformação principal dos materiais nas condições de ausência de adoçamentos
(Figura 122a) e somente o raio de adoçamento externo (Figura 122b). Entretanto, cabe
ressaltar que as soluções analíticas voltadas ao cálculo das deformações plásticas efetivas
não contabilizam os efeitos de forjamento e compressão plana que antecedem o
cisalhamento dos tarugos. Por esta razão, as previsões teóricas se mantiveram abaixo dos
valores numéricos.
Em relação ao caso de raios de adoçamento idênticos, as previsões analíticas e
numéricas obtidas foram iguais ao caso de ausência de adoçamentos (vide Figura 122c),
embora as Figuras 119c e 119d mostrem a proximidade entre as componentes cisalhante e
de dobramento para tal arranjo geométrico da matriz. A simulação computacional revelou,
a partir da distribuição horizontal das componentes de deformação plástica que o
dobramento da peça conduziu à queda da componente de cisalhante εxy para níveis
próximos aos de εx, caracterizando a ação simultânea destes modos de deformação.
186
2,0
Def. plástica efetiva
1,6
1,2
Prev. teórica
Prev. teórica
Prev. numér.
Prev. numér.
1,15
- sem taxa
- com taxa
- sem taxa
- com taxa
1,18
1,15
Φ = 90º
Rint = 0,00 mm
Rext = 0,00 mm
1,18
0,8
0,4
0,0
0
β (graus)
(a)
2,0
Def. plástica efetiva
1,6
1,2
Prev. teórica
Prev. teórica
Prev. numér.
Prev. numér.
1,03
- sem taxa
- com taxa
- sem taxa
- com taxa
1,14
1,03
Φ = 90º
Rint = 0,00 mm
Rext = 5,00 mm
1,14
0,8
0,4
0,0
38
β (graus)
(b)
Def. plástica efetiva
2,0
1,6
Prev. teórica
Prev. teórica
Prev. numér.
Prev. numér.
1,2
1,15
- sem taxa
- com taxa
- sem taxa
- com taxa
1,18
1,15
Φ = 90º
Rint = 0,00 mm
Rext = 0,00 mm
1,18
0,8
0,4
0,0
0
β (graus)
Figura 122: Previsões teóricas e numéricas de deformação plástica efetiva.
(a) sem adoçamentos; (b) adoçamento externo e (c) adoçamentos iguais.
187
5.5 INFLUÊNCIA DAS CONDIÇÕES DE ATRITO
5.5.1 Resistência ao cisalhamento relacionada às condições de atrito
A Figura 123 apresenta as previsões numéricas de tensão cisalhante e pressão de
contato obtidas a partir dos nós mais externos localizados sobre os lados esquerdo e direito
do tarugo em função das condições de atrito (representadas por µ) e assumindo-se Φ = 90º.
Pode-se observar uma inversão de sinais para as tensões cisalhantes, a qual é atribuída à
passagem do tarugo em direção ao canal de saída da matriz e está associada ao
cisalhamento simples. Além disso, a pressão de contato e a tensão cisalhante se elevaram
com o aumento de µ. Em particular, quando se assume µ = 0,20 uma condição de
aderência foi detectada sobre o lado esquerdo da peça para deslocamentos acima de
10 mm. Neste caso, as condições de atrito foram suficientemente severas para permitirem
que o material atingisse a tensão de escoamento em cisalhamento que é aproximadamente
igual a 90 MPa, conforme mostrado na Figura 123c à esquerda. Além disso, os gráficos
dispostos à esquerda da Figura 123c evidenciaram uma dispersão sobre os resultados para
deslocamentos de 1 mm. Este comportamento está relacionado ao abrupto aumento da
tensão de cisalhamento e da pressão de contato. Em matrizes cujos canais se interceptam a
90º, o tarugo inicialmente suporta uma compressão plana antes de escoar plasticamente por
cisalhamento simples. Assim, a dispersão inicial dos resultados para 1 mm de
deslocamento está ligado à resposta do ferramental devido à compressão do tarugo, que se
torna mais acentuada para níveis mais severos de atrito. Ao mesmo tempo, especificamente
para a Figura 123b localizada à esquerda, podem ser observadas dispersões de alguns
pontos referentes a 30, 40 e 45 milímetros de deslocamento. Tais desvios estão
relacionados ao dobramento de camadas do tarugo durante a sua passagem em direção à
saída da matriz. Os gráficos dispostos à direita da Figura 123 revelam o aparecimento de
valores intermediários, os quais estão associados às regiões de descarregamento
localizadas ao longo da superfície da amostra após atravessar a zona de deformações
plásticas. O fenômeno de aderência pode ser verificado quando as interfaces de contato
tarugo-matriz são analisadas separadamente. Neste contexto, a Figura 124 mostra a
evolução dos deslocamentos, pressão de contato e tensão cisalhante referente aos nós
localizados sobre a base e os lados esquerdo e direito do tarugo. Nestes casos, a condição
mais severa de atrito e configuração da matriz foram consideradas por meio dos valores de
0,20 e 90º aos parâmetros µ e Φ.
188
35
100
Lado esquerdo
Uy = - 1,00 mm
60
Tensão cisalhante (MPa)
Tensão cisalhante (MPa)
80
30
Uy = -10,00 mm
40
Uy = -20,00 mm
20
Uy = -30,00 mm
0
Uy = -40,00 mm
-20
Uy = -45,00 mm
-40
-60
-80
-100
µ = 0,05
Φ = 90º
0
25
20
µ = 0,05
Φ = 90º
15
5
Lado direito
Uy = - 1,00 mm
0
Uy = -10,00 mm
-5
Uy = -20,00 mm
10
-10
Uy = -30,00 mm
-15
Uy = -40,00 mm
-20
300
600
900
1200
1500
Pressão de contato (MPa)
-25
1800
Uy = -45,00 mm
0
100
200
300
400
500
600
Pressão de contato (MPa)
(a)
35
Lado esquerdo
Uy = - 1,00 mm
80
60
30
25
Tensão cisalhante (MPa)
Tensão cisalhante (MPa)
100
Uy = -10,00 mm
40
Uy = -20,00 mm
20
Uy = -30,00 mm
0
Uy = -40,00 mm
-20
Uy = -45,00 mm
-40
-60
-80
-100
µ = 0,10
Φ = 90º
20
15
300
600
900
1200
1500
Pressão de contato (MPa)
Lado direito
Uy = - 1,00 mm
10
5
0
Uy = -10,00 mm
-5
Uy = -20,00 mm
-10
Uy = -30,00 mm
-15
Uy = -40,00 mm
-20
Uy = -45,00 mm
-25
0
µ = 0,10
Φ = 90º
1800
0
100
200
300
400
500
600
Pressão de contato (MPa)
(b)
100
60
30
Tensão cisalhante (MPa)
Tensão cisalhante (MPa)
35
Lado esquerdo
Uy = - 1,00 mm
80
Uy = -10,00 mm
40
Uy = -20,00 mm
20
Uy = -30,00 mm
0
Uy = -40,00 mm
Uy = -45,00 mm
-20
-40
-60
µ = 0,20
Φ = 90º
-80
-100
0
300
600
900
1200
1500
25
20
15
Lado direito
Uy = - 1,00 mm
10
5
Uy = -10,00 mm
0
µ = 0,20
Φ = 90º
-5
-10
-15
1800
Pressão de contato (MPa)
Uy = -30,00 mm
Uy = -40,00 mm
-20
-25
Uy = -20,00 mm
Uy = -45,00 mm
0
100
200
300
400
500
Pressão de contato (MPa)
600
(c)
Figura 123: Tensão cisalhante e pressão de contato obtidas junto aos nós localizados
sobre os lados esquerdo e direito do tarugo. (a) µ = 0,05; (b) µ = 0,10 e (c) µ = 0,20.
189
Na Figura 124a, pode-se observar a presença de deslocamentos compressivos
sobre o lado esquerdo do tarugo que decrescem continuamente, a partir do nó superior
1347 até o nó 1345. Além disso, os nós 1491, 1451 e 1413 indicaram uma tendência de
estabilização dos deslocamentos com o tempo. Fica claro também que o nó 1345 não se
moveu, em virtude do aumento da pressão de contato desde a base até o topo da peça após
o início da prensagem, devido ao elevado valor de µ. Em relação ao nó 1347 pode-se notar
que a pressão de contato se elevou de 0 até 1,1 GPa para tempos entre 0 e 50. Este
intervalo temporal mostrou que as regiões com alta pressão de contato exibiram um caráter
mais intenso de aderência, ou seja, os nós 1347, 1491 e 1451 permaneceram aderidos, ao
passo que os nós 1413 e 1345 não apresentaram dependência à condição de agarramento.
Após este intervalo e até o término da simulação os nós revelaram um decréscimo da
pressão de contato acompanhado por um acréscimo das tensões cisalhantes. Este efeito está
ligado ao algoritmo de contato baseado no método de Lagrange aumentado. Os picos de
tensão cisalhante observados após o tempo de 300, pelos nós 1347 e 1491 estão associados
com o dobramento do tarugo durante a sua passagem pela interseção inferior dos canais.
O comportamento demonstrado pelo lado direito do tarugo foi marcado pela
contribuição positiva ao escoamento do material em direção ao canal de saída. Isto pode
ser apreciado na Figura 124b, onde se verificou um expressivo aumento dos deslocamentos
nodais desde o topo (nó 1348) até a base (nó 1346). Em relação ao atrito, o escoamento do
material ao longo da interseção dos canais se caracterizou por picos de pressão de contato e
o aumento de tensão cisalhante seguido por um descarregamento. Ainda, o encruamento
foi responsável pela elevação da pressão de contato partindo da base do tarugo e dirigindose para a porção superior, ou seja, do nó 1346 ao 1348. Em síntese, o lado direito do tarugo
foi deformado por cisalhamento simples exibindo picos de pressão de contato em relação
aos nós 1565, 1603, 1643 e 1348.
Ao longo da base, os deslocamentos nodais se mostraram pequenos quando
comparados aos lados esquerdo e direito. Este fato é uma conseqüência direta da condição
severa de atrito adotada. Além disso, o dobramento inicial do tarugo causou uma intensa
aderência sobre os nós próximos ao lado esquerdo (nós 1345 e 1355) acompanhada por
elevados níveis de cisalhamento. Partindo do nó 1362 em direção ao 1346, o caráter
positivo associado ao lado direito contribuiu para o decréscimo da pressão de contato e a
tensão cisalhante após o tempo de 50. O comportamento associado à matriz com Φ = 120º
se mostrou análoga ao caso de 90º, conforme discutido por Medeiros et al. [85].
190
2800
30
20
10
µ = 0,20
Φ = 90º
0
-10
-20
-30
-40
-50
200
Lado esquerdo
nó 1347
nó 1491
nó 1451
nó 1413
nó 1345
2400
2000
1600
µ = 0,20
Φ = 90º
Tensão cisalhante (MPa)
Lado esquerdo
nó 1347
nó 1491
nó 1451
nó 1413
nó 1345
40
Pressão de contato (MPa)
Deslocamento nodal (mm)
50
1200
800
400
0
0
100
200
Tempo
300
400
500
Lado esquerdo
nó 1347
nó 1491
nó 1451
nó 1413
nó 1345
160
120
80
40
0
-40
-80
-120
0
100
200
300
Tempo
400
µ = 0,20
Φ = 90º
0
500
100
200
Tempo
300
400
500
(a)
30
20
10
0
µ = 0,20
Φ = 90º
-10
-20
-30
320
Lado direito
nó 1348
nó 1643
nó 1603
nó 1565
nó 1346
2400
2000
1600
µ = 0,20
Φ = 90º
1200
800
400
240
200
160
120
µ = 0,20
Φ = 90º
80
40
0
-40
-80
-40
-50
Lado direito
nó 1348
nó 1643
nó 1603
nó 1565
nó 1346
280
Tensão cisalhante (MPa)
Lado direito
nó 1348
nó 1643
nó 1603
nó 1565
nó 1346
40
Deslocamento nodal (mm)
2800
Pressão de contato (MPa)
50
0
0
100
200
300
Tempo
400
-120
0
500
100
200
300
Tempo
400
0
500
100
200
300
400
500
Tempo
(b)
2,5
2,0
µ = 0,20
Φ = 90º
Pressão de contato (MPa)
Deslocamento nodal (mm)
Base
nó 1345
nó 1355
nó 1362
nó 1370
nó 1346
3,0
1,5
1,0
0,5
0,0
320
Base
nó 1345
nó 1355
nó 1362
nó 1370
nó 1346
2400
2000
1600
µ = 0,20
Φ = 90º
1200
800
400
0
0
100
200
300
Tempo
400
500
240
200
160
120
100
200
300
Tempo
400
500
µ = 0,20
Φ = 90º
80
40
0
-40
-80
-120
0
Base
nó 1345
nó 1355
nó 1362
nó 1370
nó 1346
280
Tensão cisalhante (MPa)
2800
3,5
0
100
200
300
Tempo
400
500
(c)
Figura 124: Resultados nodais de deslocamento, pressão de contato e tensão cisalhante em função do tempo de análise para Φ = 90º e µ = 0,20.
(a) lado esquerdo do tarugo; (b) lado direito do tarugo e (c) base do tarugo.
191
A interseção mais suave entre os canais foi responsável pela queda da intensidade
das tensões cisalhantes ao longo da interface peça-ferramental mesmo em condições mais
severas de atrito, conforme apresentado na Figura 125. Esta condição sugere fortemente
que a deformação plástica imposta sobre o material durante a prensagem foi menos efetiva
quando comparada ao caso em que Φ = 90º. Dessa forma, é razoável deformar o aço LI
através de uma matriz com canais interceptados a um ângulo reto e assumindo condições
de atrito abaixo de 0,20 para evitar aderência. Ainda, a interseção a 120º promoveu um
processamento menos severo sobre o tarugo e, portanto, a dispersão dos resultados se
mostrou menos intensa. Contudo, no início da prensagem a parte inferior da amostra é
suportada por uma pequena região da matriz. Conseqüentemente, um aumento da pressão
de contato durante a compressão plana da peça pode ser observado em 1 mm de
deslocamento. Por fim, as zonas de descarregamento associadas ao duplo dobramento do
tarugo podem explicar a diminuição gradual da pressão de contato evidenciada nos
gráficos dispostos à direita, na Figura 125.
100
60
35
Lado esquerdo
Uy = - 1,00 mm
µ = 0,05
Φ = 120º
30
Uy = -10,00 mm
40
Uy = -20,00 mm
20
Uy = -30,00 mm
0
Uy = -40,00 mm
Tensão cisalhante (MPa)
Tensão cisalhante (MPa)
80
Uy = -45,00 mm
-20
-40
-60
-80
-100
25
20
15
100
200
300
400
500
600
Pressão de contato (MPa)
700
Lado direito
Uy = - 1,00 mm
10
5
Uy = -10,00 mm
0
Uy = -20,00 mm
-5
Uy = -30,00 mm
-10
Uy = -40,00 mm
-15
0
µ = 0,05
Φ = 120º
800
Uy = -45,00 mm
0
100
200
300
400
500
600
Pressão de contato (MPa)
(a)
35
100
60
Lado esquerdo
Uy = - 1,00 mm
µ = 0,10
Φ = 120º
Uy = -10,00 mm
40
Uy = -20,00 mm
20
Uy = -30,00 mm
0
Uy = -40,00 mm
-20
Uy = -45,00 mm
-40
-60
-80
-100
30
Tensão cisalhante (MPa)
Tensão cisalhante (MPa)
80
25
20
15
100
200
300
400
500
600
Pressão de contato (MPa)
700
800
Lado direito
Uy = - 1,00 mm
10
5
Uy = -10,00 mm
0
Uy = -20,00 mm
-5
Uy = -30,00 mm
-10
Uy = -40,00 mm
-15
0
µ = 0,10
Φ = 120º
Uy = -45,00 mm
0
100
200
300
400
500
600
Pressão de contato (MPa)
(b)
Figura 125: Tensões cisalhantes e pressões de contato obtidas para Φ = 120º ao longo
dos lados esquerdo e direito do tarugo. (a) µ = 0,05 e (b) µ = 0,10
192
5.5.2 Dependência entre a carga de prensagem e as condições de atrito
A Figura 126 compara as previsões nodais de força determinadas para Φ igual a
90º e 120º, em função das condições de atrito. Como reportado por Dumoulin et al. [55] e
mais recentemente por Son et al. [83], o aumento do coeficiente de atrito implica em
elevações da força de prensagem. Além disso, pode-se observar o aumento da força entre 5
e 7,5 mm de deslocamento seguido por uma diminuição após cerca de 10 mm. Este efeito
corresponde à largura dos canais e se deve ao dobramento da base do tarugo para permitir
sua passagem em direção ao canal de saída da matriz. Para Φ = 90º (Figura 126a),
observou-se um pico inicial de força comum a todos os valores de µ relativo à curvatura do
material quando solicitado em compressão plana,
seguido por um imediato
descarregamento provavelmente causado pela inversão de sinais das tensões cisalhantes.
Um progressivo e aproximadamente linear aumento de carga foi também verificado
quando µ = 0,05, que se iniciou após 15 mm e se estendeu até cerca de 44 mm de
deslocamento. Por outro lado, a severidade do atrito exibiu uma queda de carga neste
domínio de deslocamentos, a qual se explica pela ocorrência de aderência ao longo do lado
direito do tarugo no interior do canal de saída. Entretanto, a evolução da força para
Φ = 120º mostra um recarregamento após 15 mm devido ao subseqüente dobramento da
amostra necessário à completa rotação do tarugo, conforme mostrado na Figura 126b.
280
280
Força (KN)
240
200
Φ = 90º
Φ = 90º
Φ = 90º
Φ = 90º
µ = 0,00,
µ = 0,05,
µ = 0,10,
µ = 0,20,
240
200
Força (KN)
µ = 0,00,
µ = 0,05,
µ = 0,10,
µ = 0,20,
160
120
80
Φ = 120º
Φ = 120º
Φ = 120º
Φ = 120º
160
120
80
40
40
0
0
0
5
10
15
20
25
30
35
40
Deslocamento do tarugo (mm)
(a)
45
50
0
5
10
15
20
25
30
35
40
45
Deslocamento do tarugo (mm)
50
(b)
Figura 126: Dependência entre a carga e as condições de atrito. (a) Φ=90º e (b) Φ=120º.
193
5.5.3 Distribuição das tensões e deformações plásticas efetivas
A Figura 127 apresenta a distribuição das grandezas efetivas plásticas de tensão e
deformação determinadas para Φ igual a 90º e 120º, assumindo-se µ = 0,20. A 90º, nota-se
que os menores valores de deformação plástica efetiva localizaram-se na porção inferior do
tarugo, uma vez que tais regiões não atravessaram a zona de deformação delimitada pela
interseção dos canais. Por outro lado, a ausência de adoçamentos promoveu um
dobramento da malha do tarugo e conduziu a um valor de deformação plástica efetiva
próximo a 4. Por fim, as regiões uniformes de ε foram originadas pelas linhas de tensão
efetiva normais à direção de aplicação dos deslocamentos mostradas na Figura 127b. Esta
característica da tensão efetiva foi observada por Kim et al. [50] e se apóia também nas
respectivas curvas de atrito apresentadas na Figura 125c.
A 120º, os aspectos observados podem ser explicados por analogia ao caso prévio,
ou seja, as extremidades do tarugo forneceram as menores previsões de deformação
plástica efetiva, de acordo com a Figura 127c. Em contrapartida, a presença das linhas de
tensão efetiva perpendiculares à direção da aplicação dos deslocamentos, mostradas na
Figura 127d, explicam a zona uniforme de deformação plástica efetiva observada.
(a)
(b)
(c)
(d)
Figura 127: (a) distribuição de ε para Φ=90º; (b) distribuição de tensões efetivas,Φ=90º;
(c) distribuição de ε para Φ=120º e (d) distribuição de tensões efetivas para Φ=120º.
194
5.5.4 Mapeamento nodal da deformação plástica efetiva na zona uniforme
A Figura 128 apresenta as previsões nodais de deformação plástica efetiva obtidas
ao longo da zona homogênea de deformações associadas às matrizes com Φ igual a 90º e
120º, considerando as direções vertical e horizontal.
O caso em que Φ assumiu 90º e µ = 0,05 permitiu observar a independência entre
ε e as condições de atrito ao longo das direções consideradas já que um valor próximo a
1,15 foi obtido sobre a metade da zona de deformação (50% da zona uniforme). Esta
relativa invariância apresentou considerável concordância com os modelos teóricos
propostos por Eivani et al. [43]. Os autores observaram que a solução teórica voltada ao
cálculo das deformações plásticas efetivas são funções que dependem exclusivamente da
geometria da matriz. Em relação à Figura 128a, cabe destacar a presença de uma zona
homogênea de deformações ao longo da direção horizontal. Fica claro que o início e o
término mostraram baixos valores de ε em razão da influência das bordas do tarugo. Por
outro lado, as porções de 25, 50 e 75% forneceram elevada homogeneidade na distribuição
desta grandeza efetiva, o que concorda com os resultados obtidos por Yoon et al. [84]. A
direção vertical revelou que somente o início da zona uniforme apresentou pequenos
valores de deformação plástica efetiva, já que os efeitos de borda foram menos
pronunciados.
Para µ = 0,10, uma razoável heterogeneidade na distribuição de ε foi observada
ao longo da direção horizontal e pode ser explicada pelas perturbações induzidas ao
material em função do contato com a matriz. Por esta razão, o máximo valor de
deformação plástica efetiva foi observado em 100% da zona uniforme, conforme mostra a
Figura 128b. Em relação à direção vertical o pequeno efeito de borda resultou em uma
tendência análoga ao caso anterior de lubrificação ideal.
A condição mais severa de atrito (µ = 0,20) causou oscilações mais acentuadas ao
longo da direção horizontal, como mostra a Figura 128c. Estas oscilações foram
intensificadas pela condição de agarramento quando o material se deformou plasticamente
ao se deslocar em direção ao canal de saída da matriz. Em contrapartida, algumas regiões
revelaram alta homogeneidade ao longo da direção vertical, ou seja, as porções referentes a
25% até 75% da zona uniforme. No início e no final desta zona uniforme, observou-se um
efeito de proximidade entre o tarugo e a matriz, o qual resultou em uma distribuição
heterogênea das deformações plásticas efetivas.
195
2,4
1,6
1,2
0,8
0,4
0,0
µ = 0,05; Φ = 90º
0
4
8
12
16
20
24
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
2,0
Def. plástica efetiva
2,0
Def. plástica efetiva
2,4
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
28
1,6
1,2
0,8
0,4
0,0
32
Distância horizontal (mm)
36
40
µ = 0,05; Φ = 90º
0
2
4
6
8
10
12
14
16
18
14
16
18
14
16
18
Distância vertical (mm)
(a)
2,4
2,4
Def. plástica efetiva
2,0
1,6
Def. plástica efetiva
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
1,2
0,8
1,6
1,2
0,8
0,4
0,4
0,0
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
2,0
µ = 0,10; Φ = 90º
0
4
8
12
16
20
24
28
32
Distância horizontal (mm)
36
0,0
40
µ = 0,10; Φ = 90º
0
2
4
6
8
10
12
Distância vertical (mm)
(b)
2,4
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
2,0
1,6
1,2
0,8
0,4
0,0
µ = 0,20; Φ = 90º
0
4
8
12
16
20
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
2,0
Def. plástica efetiva
Def. plástica efetiva
2,4
24
28
32
Distância horizontal (mm)
36
40
1,6
1,2
0,8
0,4
0,0
µ = 0,20; Φ = 90º
0
2
4
6
8
10
12
Distância vertical (mm)
(c)
Figura 128: Previsões nodais de ε ao longo da zona plástica uniforme para distintas
condições de atrito e Φ = 90º. (a) µ = 0,05; (b) µ = 0,10 e (c) µ = 0,20.
196
A interseção dos canais a 120º mostrou também a influência de parâmetros
geométricos sobre as previsões de deformação plástica efetiva, uma vez que o valor
máximo obtido foi próximo a 0,7, conforme apresentado na Figura 129. Este resultado se
mostrou condizente com as previsões obtidas por Eivani et al. [43]. Nos casos de
lubrificação ideal e atrito mais severo (µ = 0,10), a ausência de aderência resultou em um
apreciável grau de homogeneidade na distribuição de ε . A inexistência de oscilações ao
longo da zona uniforme confirmou este comportamento, principalmente ao longo da
direção horizontal onde o efeito da aderência se mostrou mais intensivo. Contudo, quando
se adotou µ = 0,20 os efeitos oscilatórios ao longo da direção horizontal se tornaram
evidentes e resultaram em um grau significativo de heterogeneidade das deformações que
compreendeu a totalidade da superfície deformada do tarugo. A direção vertical, por sua
vez, manteve o caráter homogêneo da distribuição das deformações plásticas efetivas,
assim como observado previamente para Φ = 90º.
2,4
2,4
Def. plástica efetiva
2,0
1,6
Def. plástica efetiva
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
1,2
0,8
0,4
0,0
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
2,0
1,6
1,2
0,8
0,4
µ = 0,05; Φ = 120º
0
4
8
12
16
20
24
28
32
Distância horizontal (mm)
36
0,0
40
µ = 0,05; Φ = 120º
0
2
4
6
8
10
12
14
16
18
16
18
Distância vertical (mm)
(a)
2,4
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
2,0
1,6
1,2
0,8
0,4
0,0
µ = 0,10; Φ = 120º
0
4
8
12
16
20
Início da zona uniforme
25% da zona uniforme
50% da zona uniforme
75% da zona uniforme
100% da zona uniforme
2,0
Def. plástica efetiva
Def. plástica efetiva
2,4
24
28
32
Distância horizontal (mm)
36
40
1,6
1,2
0,8
0,4
0,0
µ = 0,10; Φ = 120º
0
2
4
6
8
10
12
14
Distância vertical (mm)
(b)
Figura 129: Previsões nodais de ε ao longo da zona plástica uniforme para diferentes
condições de atrito e Φ = 120º. (a) µ = 0,05; (b) µ = 0,10 e (c) µ = 0,20.
197
5.6 COMPARAÇÕES ENTRE MODELOS 2D e 3D
A Figura 130 apresenta a comparação entre as previsões numéricas, fornecidas
pelos modelos 2D e 3D propostos, e experimentais de força de prensagem em função do
deslocamento do tarugo para a liga de alumínio Al 1100. Para tanto, considerou-se Φ = 90º
e um raio de adoçamento externo igual a 5 mm (β ~ 37º). Em relação ao atrito, assumiu-se
a condição de lubrificação ideal com µ = 0,05. Além disso, se comparam os valores
numéricos máximos (pontos A’ e A”) à maior previsão experimental de carga (ponto A),
conforme mostrado na Figura 130b.
A presença de um adoçamento externo mais acentuado impôs à curva
experimental de carga aumentos sucessivos de força, após ~ 12 e 25 mm de deslocamento
do tarugo, seguidos por um patamar até 30 mm e um subseqüente decréscimo que se
estendeu até o final estabelecido ao experimento de cerca de 40 mm de deslocamento.
Considerando a geometria do tarugo com seção quadrada de lado igual a 10 mm e altura de
50 mm, a elevação de carga após 12 mm está relacionada ao dobramento necessário à
passagem da base da amostra em direção ao canal de saída da matriz. Para este dobramento
a força aumentou de 0 kN a 20 kN. A continuação do experimento até a passagem da
metade da altura do tarugo em direção ao canal de saída resultou em uma pequena
elevação de carga de 20 kN para o valor máximo de 23 kN sobre o ponto A (Figura 130a),
o que demonstra um regime estabelecido de deformações. Os subseqüentes
comportamentos de patamar até 30 mm e a queda de carga até o fim do ensaio
caracterizaram o movimento de corpo rígido do tarugo ao longo do canal de saída da
matriz, ou seja, a ausência de deformação plástica nesta região.
A curva força x deslocamento fornecida pelo modelo numérico 2D, apesar de
demonstrar uma forma bastante similar ao caso experimental, com acréscimos alternados
de carga após cerca de 12 mm e 20 mm e a queda depois de 25 mm até 40 mm, originou
resultados inferiores de carga. A explicação para tal comportamento é o fato de se manter
µ = 0,05 ao longo de todas as interfaces de contato peça-ferramental no modelamento
numérico. Ao mesmo tempo, em deformação plana, se tem um número menor de interfaces
de contato peça-ferramental, o que contribuiu também para a queda de carga observada. Na
prática, a lubrificação se torna heterogênea durante a deformação do material e conduz a
acréscimos localizados de carga.
198
O modelo numérico tridimensional originou uma curva de carga que pode ser
considerada como uma superposição daquela obtida em duas dimensões até cerca de
20 mm, pelos aumentos sucessivos de carga até o valor máximo de 23 kN obtido junto ao
ponto A”. Entretanto, a queda sistemática da força de prensagem após A” até o término da
simulação (40 mm) evidenciou a maior dependência deste modelo às condições de atrito e
aos efeitos de descarregamento elástico e saturação das deformações plásticas efetivas.
40
Previsão numérica (MEF - 3D)
Previsão numérica (MEF - 2D_EPD)
Experimental
35
Força (kN)
30
25
A" A
20
A'
15
10
Φ = 90º
β = 38º
µ = 0,05
5
0
0
5
10
15
20
25
30
35
40
45
Deslocamento do tarugo (mm)
50
(a)
40
36
Força ( kN)
32
Previsão numérica (MEF - 2D_EPD)
Previsão numérica (MEF - 3D)
Experimental
28
24
20
23,00
23,00
17,53
16
12
8
4
0
38
β (graus)
(b)
Figura 130: (a) curvas numéricas e experimental de carga e (b) valores numéricos e
experimental máximos de força.
A Figura 131 apresenta a distribuição das grandezas plásticas efetivas resultante
dos modelos 2D (deformação plana) e 3D desenvolvidos para a prensagem da liga
Al 1100. Pode-se notar que ambos os modelos mostram uma considerável similaridade
entre a distribuição e os valores obtidos para tais grandezas. Segundo Kim et al. [50], a
propagação das tensões efetivas junto à interseção dos canais, na direção horizontal explica
a formação da zona homogênea com distribuição uniforme das deformações efetivas.
199
Deve-se ressaltar que o valor máximo de tensão efetiva observado nas Figuras 131a e 131c
se refere ao máximo de 1,16 adotado para ε na curva de encruamento utilizada nas
simulações. Isto reforça novamente a limitação desta curva em reproduzir a deformação
por cisalhamento imposta ao material durante cada passe de prensagem.
(a)
(b)
(c)
(d)
Figura 131: Distribuição das grandezas plásticas efetivas ao longo da superfície da peça.
(a) 2D tensão; (b) 2D deformação; (c) 3D tensão e (d) 3D deformação.
Comparando-se os modelos 2D e 3D, é importante reforçar que o primeiro
apresenta menos superfícies de contato entre o tarugo e a ferramenta que o segundo, além
de não possuir todas as componentes de tensão e deformação, em virtude da aproximação
ao estado plano de deformações. Portanto, as previsões de carga associadas devem ser
menores do que as obtidas com o modelo em três dimensões. Contudo, pelos resultados
apresentados, a abordagem bidimensional pode ser empregada no estudo da prensagem de
materiais via a técnica PCEA com a vantagem de um tempo computacional reduzido. A
discussão do tempo computacional é extremamente válida em processos altamente
não-lineares, como é o caso daqueles que envolvem plasticidade e atrito. No caso
particular da prensagem em canais equiangulares, o tempo médio de duração da simulação
a partir do modelo 2D foi de 4 horas. Já o modelo 3D necessitou de aproximadamente 7
horas para a completa solução do problema. Portanto, em termos de esforço
computacional, fica evidente também a validade do modelamento da técnica PCEA
aproximado à condição de deformação plana.
200
6. CONCLUSÕES
6.1 MODELAMENTO ANALÍTICO DA TÉCNICA PCEA
O modelamento analítico proposto para a previsão da carga de prensagem para
materiais com pequena sensibilidade à taxa de deformação a frio, como as ligas Al 6070 e
Al 1100, mostrou que os efeitos causados pelas condições de atrito prevalecem sobre os
demais parâmetros considerados nesta tese, sobretudo à medida que a fricção se torna mais
severa. Ademais, evidenciou-se o acoplamento entre escoamento plástico e tribologia, ao
serem combinadas às condições de atrito a critérios de escoamentos distintos. Portanto,
observou-se que o acréscimo da pressão normalizada seguiu o mesmo sentido do aumento
do fator de atrito ou a mudança da descrição isotrópica de Drucker para o critério de
von Mises. De fato, o achatamento da superfície de escoamento entre as regiões de tração e
ou compressão plana e cisalhamento puro pode ser considerado como o principal
parâmetro que controla os estados de tensões e deformações obtidos via a técnica PCEA.
Este comportamento plástico pode ser verificado ao serem comparadas as previsões de
carga oriundas destes critérios de escoamento com o resultado experimental obtido após a
prensagem a frio da liga de alumínio Al 1100 em um único passe. Dentre os parâmetros
geométricos avaliados, verificou-se que o ângulo Φ de interseção dos canais exerce maior
influência sobre as previsões de pressão em comparação aos raios de adoçamento. Ainda,
observou-se que aumento do raio de adoçamento interno resulta em uma elevação de carga
por diminuir as previsões de β. Entretanto, o aumento do raio externo provoca a elevação
do ângulo β e conduz à diminuição da carga de prensagem.
O cálculo das deformações efetivas revelou a correção de 1/√3 para os critérios de
Drucker e von Mises em cisalhamento puro. O seu caráter geométrico mostrou a relevância
do ângulo Φ sobre os adoçamentos. Assim, a matriz responsável por níveis satisfatórios de
deformação efetiva e carga corresponde ao caso de Φ = 90º e Rext igual a 5 mm.
201
6.2 PLANEJAMENTO FATORIAL 2k
O método fatorial 2k se mostrou útil na avaliação da relevância dos parâmetros
geométricos, critérios de escoamento plástico, tribológicos e de processamento sobre as
previsões de pressão e deformação plástica efetiva oriundas do processamento da liga
Al 6061 por meio do processo PCEA. Em relação à pressão, o gráfico de probabilidades
demonstrou que as condições de atrito desempenharam a maior relevância dentre os
parâmetros analisados. Por outro lado, a sensibilidade à geometria da matriz foi mais
evidente para variações do ângulo de interseção dos canais do que ao serem variados os
raios de adoçamento. Ademais, foi possível evidenciar o aumento de pressão associado ao
acréscimo da taxa de deformação e a existência do acoplamento entre parâmetros
tribológicos e de escoamento plástico. Estes aspectos foram confirmados, em primeiro
lugar, pela análise de variância e, em seguida, pela superfície de resposta multilinear
proposta para a pressão necessária a prensagem em canais equiangulares.
No que se refere à deformação plástica efetiva, o gráfico de probabilidades
permitiu verificar a sua extrema dependência às variações no ângulo de interseção dos
canais e, em menor grau, quando são modificados os raios de adoçamento. Sendo assim,
o caráter geométrico da solução analítica proposta no presente trabalho foi confirmado.
Da mesma forma que para o caso da pressão, a análise de variância e a superfície de
resposta contribuíram de forma decisiva para a classificação dos parâmetros de relevância
sobre a deformação plástica efetiva indicada pelo gráfico de probabilidades.
Além de permitir as identificações de parâmetros que exercem influências sobre
as soluções analíticas propostas para os cálculos de carga e deformações plásticas efetivas,
à análise fatorial 2k indicou a necessidade de exploração de algumas configurações
geométricas da matriz, com interseção a 90º, associadas à condição de lubrificação ideal e
assumindo-se a velocidade típica de prensagem igual a 1 mm / s. Neste sentido,
considerando-se as superfícies de resposta determinadas para pressão e deformação
plástica efetiva e a coerência demonstrada pelos resultados encontrados face à literatura,
pode-se concluir que a análise qualitativa da técnica PCEA via a análise fatorial 2k
permitiu uma correta classificação dos diversos parâmetros considerados quanto à
importância que exercem sobre as variáveis de interesse avaliadas neste trabalho. Enfim,
a indicação das configurações geométricas da matriz que deveriam ser analisadas com
maior ênfase justificou a adoção do método fatorial 2k aplicado à deformação via PCEA.
202
6.3 MODELAMENTO NUMÉRICO DA TÉCNICA PCEA
6.3.1 Modelos bidimensionais: prensagem da liga de alumínio Al 6070
Na ausência de raios de adoçamento com interseção dos canais a 90º, foram
realizadas simulações de um único passe sobre a liga Al 6070 a partir de considerações
distintas da curva de encruamento avaliada em compressão uniaxial, a saber, para os
valores de deformação plástica efetiva resultantes da sua extrapolação máxima de 1,16 e
correspondente ao expoente de encruamento (0,26), respectivamente. Em seguida, as
previsões numéricas de carga de prensagem foram comparadas aos resultados
experimentais obtidos por Eivani et al. [43]. As curvas oriundas das simulações revelaram
um rápido aumento inicial de carga, associado à compressão plana experimentada pelo
material ao ser forçado a escoar plasticamente em direção ao canal de saída da matriz,
acompanhado por decréscimo da força de prensagem que se estendeu até o final da
simulação. Entretanto, a curva extrapolada até 1,16 evidenciou o correto modelamento do
comportamento plástico do material ao fornecer resultados de carga de prensagem
comparáveis aos valores experimentais determinados por Eivani et al. [43].
Em relação às deformações plásticas efetivas, a análise da condição de
plasticidade confirmou a abordagem correta para a simulação da técnica PCEA quando se
estende a capacidade de encruamento do material, uma vez que os efeitos de
descarregamento elástico e saturação da grandeza efetiva de deformação se acentuaram
sobre o material com menor capacidade de encruamento e acentuaram a queda de carga.
Outra conclusão importante diz respeito à limitação da curva de encruamento obtida sob
tração / compressão uniaxiais na representação deste processo de conformação que é
governado, principalmente, pelo cisalhamento simples.
O efeito do raio de adoçamento externo sobre a força de prensagem confirmou a
queda da carga em relação à ausência de adoçamentos. As respectivas curvas de carga
exibiram um rápido aumento inicial da força seguido pelo seu decréscimo, o que é
explicado pelo descarregamento elástico e a saturação das deformações plásticas efetivas.
Os valores próximos de saturação associados a estes modelos permitiram concluir que o
cisalhamento simples governou a deformação do tarugo para esta geometria de matriz.
203
6.3.2 Modelos bidimensionais: influência da viscoplasticidade na carga de prensagem
Adotando-se a condição de lubrificação ideal e arranjos geométricos da matriz que
envolvem a ausência de raios de adoçamento, presença somente do raio de adoçamento
externo e raios de adoçamentos idênticos, verificou-se que a inclusão dos efeitos
viscoplásticos definidos pela lei de encruamento de Peirce ao material modelo conduziu a
um leve aumento na previsões da carga de prensagem para todos os casos geométricos
analisados, pela comparação aos resultados obtidos quando apenas o encruamento plástico
definido pela lei de Hollomon é considerado. Este comportamento foi confirmado por meio
da comparação entre as respectivas previsões numéricas da tensão efetiva calculadas com o
critério de plasticidade de von Mises, já que a inclusão da viscoplasticidade acarreta o
aumento da tensão de escoamento do material e, por conseguinte, eleva a sua resistência ao
escoamento plástico acompanhada pelo acréscimo das tensões efetivas.
Os efeitos individuais da geometria da matriz mostraram que a condição mais
severa de prensagem é aquela em ausência de raios de adoçamento. Além disso, o raio de
adoçamento externo (Rext) contribuiu para o decréscimo de carga enquanto o raio de
adoçamento interno (Rint) causou a sua elevação. O aumento de carga associado à presença
de raios de adoçamento idênticos levantou a hipótese de que o tarugo é deformado por uma
combinação entre cisalhamento simples e dobramento.
A investigação por meio do mapeamento nodal das componentes de deformação
plástica ao longo das superfícies deformadas dos tarugos mostrou que, para ambas as
descrições de comportamento plástico, os casos de ausência de adoçamentos e adoçamento
externo revelaram as mais altas previsões de deformação plástica associadas à componente
de cisalhamento, em ambas as direções. Por outro lado, no caso particular de adoçamentos
idênticos, a componente cisalhante se mostrou abaixo da grandeza efetiva e mais próxima à
componente x atuante ao longo da direção horizontal e responsável pelo dobramento do
tarugo. Dessa forma, conclui-se que esta configuração geométrica da matriz atribui aos
materiais a deformação plástica combinada por cisalhamento simples e dobramento.
Por fim, comparando-se as previsões analíticas e numéricas de carga e
deformação plástica efetiva permitiu validar a inclusão dos efeitos viscoplásticos no
cálculo da carga em função do seu aumento em relação ao material independente destes.
Além disso, a comparação entre as previsões analíticas e numéricas de deformação plástica
efetiva confirmou a sua exclusiva dependência às alterações geométricas no ferramental.
204
6.3.3 Modelos bidimensionais: condições tribológicas críticas na técnica PCEA
As curvas tensão cisalhante x pressão obtidas após a simulação da prensagem a
frio de um aço LI (Livre de Intersticiais) após um único passe permitiram observar, tanto a
90º como a 120º, uma condição crítica de aderência quando o coeficiente de atrito estático
(µ) assumiu o valor de 0,20. Esta condição promoveu um acréscimo da força de prensagem
necessária à passagem do tarugo em direção ao canal de saída da matriz. Ao mesmo tempo,
os níveis de deslocamentos nodais, pressões de contato e tensões cisalhantes confirmaram
uma condição de agarramento para µ = 0,20, independente do valor adotado para o ângulo
Φ de interseção dos canais da matriz.
A distribuição das deformações plásticas efetivas ao longo da superfície
deformada do tarugo evidenciou a presença de uma zona uniforme estendida de
deformações plásticas. Portanto, tal efeito não representa somente uma conseqüência das
linhas de fluxo de tensões efetivas de von Mises normais à direção de aplicação dos
carregamentos mas também se deve à combinação entre pressão de contato e tensão
cisalhante ao longo das interfaces de contato tarugo-matriz.
Os resultados do mapeamento nodal da distribuição das deformações plásticas
efetivas ao longo da superfície deformada do tarugo mostraram satisfatória concordância
com a literatura para ambos os casos geométricos da matriz investigados. Contudo, foi
possível verificar a presença de oscilações, para a condição mais severa de atrito, sobre as
zonas de deformação distribuídas ao longo da direção horizontal da superfície deformada
do tarugo. Tais oscilações estão associadas à aderência ao longo das interfaces de contato.
Finalmente, considerando as curvas pressão de contato x tensão cisalhante e o
mapeamento da distribuição das deformações plásticas efetivas ao longo da zona uniforme
de deformação, foi possível concluir que a melhor condição para se deformar materiais via
a técnica PCEA é aquela em que se utiliza uma matriz com canais interceptados a 90º
combinada a um valor do coeficiente µ igual ou menor a 0,10.
205
6.3.4 Comparação entre os modelos bidimensionais (2D) e tridimensionais (3D)
A comparação entre as previsões numéricas (2D e 3D) e experimentais de carga
para a liga de alumínio Al 1100 foi realizada a partir de uma matriz com Φ = 90º e um raio
de adoçamento externo de 5 mm, além de se assumir a lubrificação ideal com µ = 0,05.
A curva de carga x deslocamento obtida a partir do modelo numérico
bidimensional apresentou uma forma bastante similar àquela obtida experimentalmente,
caracterizada por aumentos alternados de carga seguido pela sua queda. A partir deste
comportamento, pode-se concluir que a queda nas previsões de força está diretamente
ligada aos efeitos do descarregamento elástico e saturação das deformações efetivas.
O modelo tridimensional forneceu uma curva de carga parcialmente próxima
àquela resultante do modelamento bidimensional. Todavia, a queda contínua da força de
prensagem mostrou sua maior dependência em relação às condições de atrito e aos efeitos
de descarregamento elástico e saturação de deformações plásticas efetivas.
A distribuição das grandezas plásticas efetivas de tensão e deformação, por sua
vez, se revelou praticamente a mesma para ambos os modelos numéricos. Esta
característica reforçou ainda mais a conclusão prévia da sua validade.
Finalmente, comparando-se os modelos 2D e 3D, observa-se que o fato de o
primeiro apresentar um menor número de superfícies de contato entre o tarugo e a
ferramenta e não apresentar todas as componentes de tensão e deformação contribui para o
decréscimo da carga de prensagem. Contudo, a aproximação bidimensional ao estado
plano de deformações pode ser empregada no estudo da técnica PCEA com a vantagem de
um tempo computacional reduzido.
206
7. SUGESTÕES PARA TRABALHOS FUTUROS
No que diz respeito aos modelos teóricos propostos para os cálculos de carga são
possíveis melhorias em escalas distintas, ou seja, macroscópica e mesoscópica. Em escala
macroscópica, apontam-se a inclusão do efeito de contrapressão exercido sobre o tarugo
por meio de um punção colocado no canal de saída da matriz, a consideração da
dependência entre a resistência ao escoamento plástico dos materiais com a geometria da
matriz e a introdução dos efeitos térmicos de forma a estender o uso das soluções analíticas
à classe de materiais que necessitam ser processados a morno, como no caso das
simulações da prensagem do titânio puro conduzidas por Jiang et al. [66]. De acordo com a
formulação teórica do método do limite superior, a parcela de contrapressão é interpretada
como uma força de superfície aplicada ao tarugo. Sendo assim, este parâmetro dever ser
inserido no cálculo da taxa de trabalho externo como um dado de entrada conhecido para
manter a carga como única variável a ser determinada. Vale destacar que
Stolyarov et al. [86] verificaram, experimentalmente, que a contrapressão promoveu
melhorias de conformabilidade e propriedades mecânicas (resistência e microdureza) sobre
a liga de alumínio Al 5083. Para associar o calor gerado ao longo das interfaces de contato
peça-ferramental à previsão de carga fornecida pelo método do limite superior,
Johnson et al. [87] apresentaram uma alternativa, simplificada ao caso adiabático, na qual a
quantidade de calor gerado durante um processo de conformação, corrigida pelo seu
rendimento, é proporcional à taxa de trabalho plástico interno. Uma vez que para as
expressões destinadas aos cálculos dos trabalhos internos associados a cada configuração
de matriz são conhecidas, podem-se estimar as respectivas variações de temperatura com
base nas propriedades térmicas de capacidade calorífica e densidade do material.
207
Em relação ao cálculo das deformações plásticas efetivas, fica evidente a
introdução dos efeitos de atrito nas soluções analíticas propostas. Eivani et al. [44]
indicaram, recentemente, uma alternativa a este respeito a partir da minimização da
solução destinada à previsão teórica de carga. Esta abordagem possibilitou aos autores
explicitar a dependência da deformação plástica efetiva com o atrito. Por analogia, a
dependência entre a deformação efetiva e a tribologia, segundo a solução analítica proposta
neste trabalho, poderia ser obtida a partir da minimização dos modelos voltados à previsão
de carga em relação ao ângulo que delimita a zona de deformação em presença de
adoçamentos. Em escala mesoscópica, indica-se a estimativa da tensão de escoamento e,
por conseguinte, da carga de prensagem por meio da lei de Voce estabelecida a partir do
modelo baseado na evolução da densidade de discordâncias com a deformação plástica
efetiva proposto por Mecking et al. [88].
Referindo-se à parte numérica, a aproximação bidimensional em condições de
deformação plana pode ser empregada no desenvolvimento de modelos discretizados por
elementos finitos que incluam os efeitos de contrapressão e temperatura. O trabalho
desenvolvido por Son et al. [65], no qual a simulação numérica da prensagem de tarugos
por meio de um aparato que inclui um punção responsável pelo efeito da contrapressão,
mostrou um aumento considerável na homogeneidade de deformações plásticas efetivas
decorrente deste procedimento. Por outro lado, as simulações numéricas do processamento
a morno de ligas à base de magnésio, conduzidas por Figueiredo et al. [57], mostraram
resultados consistentes em termos da distribuição das deformações plásticas efetivas.
Dessa forma, a consideração dos efeitos térmicos na prensagem via PCEA estende as
possibilidades à classe de materiais de difícil processamento em temperatura ambiente.
Finalmente, estendendo-se estes modelos numéricos ao caso tridimensional, os
efeitos impostos ao material pelas rotas de processamento A, B e C poderiam ser
verificados. Em primeiro lugar, deve-se introduzir uma curva que possibilite a geração de
encruamento após cada passe de prensagem. Os modelos de Mecking et al. [88] se
constituem em uma alternativa para esta finalidade. Em seguida, os modelos numéricos em
três dimensões devem contemplar a retirada do tarugo entre passes sucessivos de
prensagem para reproduzir os testes experimentais de forma consistente. Além disso, a
retirada da amostra deve ser acompanhada pela simulação de um ensaio, como o de tração
uniaxial, visando comparar as previsões numéricas e analíticas da tensão de escoamento.
208
8. REFERÊNCIAS
[1] VALIEV, R.Z. Ultrafine-grained materials prepared by severe plastic deformation.
Annales de Chimie Science des Materiaux, 1996, 369p.
[2] VALIEV, R.Z., ALEXANDROV, I.V., ISLAMGALIEV, R.K. Nanocrystalline
Materials: Science and Technology, 1998, 121 p.
[3] VALIEV, R.Z., ISLAMGALIEV, R.K., ALEXANDROV, I.V. Bulk nanostructured
materials from severe plastic deformation. Progress in Materials Science, v. 45,
p. 103-189, 2000.
[4] SEGAL, V.M. Methods of stress-strain analysis in metal-forming. Tese de Doutorado,
Minsk, 1974.
[5] SEGAL, V.M., REZNIKOV, V., DROBYSHEVKIY, A. et al. Plastic working of
metals by simple shear. Russian Metallurgy, v. 1, p. 99-105, 1981.
[6] SEGAL, V.M. Materials processing by simple shear. Materials Science and
Engineering A, v. 197, p. 157-164, 1995.
[7] SEGAL, V.M. Engineering and commercialization of equal channel angular extrusion
(ECAE). Materials Science and Engineering A, v. 386, p. 269-276, 2004.
[8] BRIDGEMAN, P.W. Studies in Large Plastic Flow and Fracture. McGraw-Hill,
New York, 1952.
[9] RICHMOND, O., DEVENPECK, M.L. A die profile for maximum efficiency in strip
drawing. In: Proceedings of the 4th US National Congress of Applied Mechanics, 1962.
[10] VALIEV, R.Z., IVANISENKO, Y.V., RAUCH, E.F. et al. Structure and deformation
behaviour of Armco iron subjected to severe plastic deformation. Acta Materialia,
v. 44, p. 4705-4712, 1996.
[11] VALIEV, R.Z. Synthesis and processing of nanocrystalline powder. David L. Bourell,
editors. 1996, 153 p.
209
[12] ALEXANDROV, I.V., ZHU, Y.T., LOWE, T.C. et al. Consolidation of nanometer
sized powders using severe plastic torsional straining. Nanostructured Materials, v. 10,
p. 45-54, 1998.
[13] ALEXANDROV, I.V., ZHU, Y., LOWE, T.C. et al. Microstructures and properties of
nanocomposites obtained through SPTS consolidation of powders. Metallurgical and
Materials Transactions A, v. 29, p. 2253-2260, 1998.
[14] FURUKAWA, M., HORITA, Z., NEMOTO, M. et al. Processing of metals by
equal-channel angular pressing. Journal of Materials Science, v. 36, p. 2835-2843,
2001.
[15] SRINIVASAN, R. Computer simulation of the equichannel angular extrusion (ECAE)
process. Scripta Materialia, v. 44, p. 91-96, 2001.
[16] VALIEV, R.Z., LANGDON, T.G. Principles of equal-channel angular pressing as a
processing tool for grain refinement. Progress in Materials Science, v. 51, p. 881-891,
2006.
[17] WANG, J., IWAHASHI, Y., HORITA, Z. et al. An investigation of microstructural
stability in an al-mg alloy with submicrometer grain size. Acta Materialia, v. 44,
p. 2973-2982, 1996.
[18] FURUKAWA, M., IWAHASHI, Y., HORITA, Z. et al. Structural evolution and the
hall-petch relationship in an Al-Mg-Li-Zr alloy with ultra-fine grain size.
Acta Materialia, v. 45, p. 4751-4757, 1997.
[19] VALIEV, R.Z. Structure and mechanical properties of ultrafine-grained metals.
Materials Science and Engineering A, v. 234-236, p. 59-66, 1997.
[20] MARKUSHEV, M.V., MURASHKIN, M.Y., PRANGNELL, P.B. et al. Structure and
mechanical behaviour of an Al-Mg alloy after equal channel angular extrusion.
NanoStructured Materials, v. 12, p. 839-842, 1999.
[21] GIBBS, M.A., HARTWIG, K.T., CORNWELL, L.R. et al. Texture formation in bulk
iron processed by simple shear. Scripta Materialia, v. 39, p. 1699-1704, 1998.
[22] SHIN, D.H., KIM, W.J., CHOO, W.Y. Grain refinement of a commercial 0.15% C
steel by equal-channel angular pressing. Scripta Materialia, v. 41, p. 259-262, 1999.
[23] SHIN, D.H., KIM, B.C., PARK, K.T. et al. Microstructural changes in equal channel
angular pressed low carbon steel by static annealing. Acta Materialia, v. 48,
p. 3245-3252, 2000.
210
[24] SHIN, D.H., SEO, C.W., KIM, J. et al. Microstructures and mechanical properties of
equal-channel angular pressed low carbon steel. Scripta Materialia, v. 42, p. 695-699,
2000.
[25] ZHU, Y.T., LOWE, T.C. Observations and issues on mechanisms of grain refinement
during ECAP process. Materials Science and Engineering A, v. 291, p. 46-53, 2000.
[26] IWAHASHI, Y., HORITA, Z., NEMOTO, M. et al. Microstructural characteristics of
ultrafine-grained aluminum produced using equal-channel angular pressing.
Metallurgical and Materials Transactions A, v. 29, p. 2245-2252, 1998.
[27] IWAHASHI, Y., HORITA, Z., NEMOTO, M. et al. An investigation of
microstructural evolution during equal-channel angular pressing. Acta Materialia,
v. 45, p. 4733-4741, 1997.
[28] PRANGNELL, P.B., GHOLINIA, A., MARKUSHEV, V.M. Investigations and
Applications of Severe Plastic Deformation, Kluwer Academic Publisher, Dordrecht.
2000, 7 p.
[29] FURUKAWA, M., IWAHASHI, Y., HORITA, Z. et al. The shearing characteristics
associated
with
equal-channel
angular
pressing.
Materials
Science
and
Engineering A, v. 257, p. 328-332, 1998.
[30] DALLA TORRE, F., LAPOVOK, R., SANDLIN, J. et al. Microstructures and
properties of copper processed by equal channel angular extrusion for 1–16 passes.
Acta Materialia, v. 52, p. 4819-4832, 2004.
[31] DALLA TORRE, F., GAZDER, A.A., PERELOMA, E.V. et al. Recent progress on
the study of the microstructure and mechanical properties of ECAE copper.
Journal of Materials Science, v. 42, p. 9097-9111, 2007.
[32] XU, C., LANGDON, T.G. The development of hardness homogeneity in aluminum
and an aluminum alloy processed by ECAP. Journal of Materials Science, v. 42,
p. 1542-1550, 2007.
[33] STOLYAROV, V.V., SHUSTER, L.Sh., MIGRANOV, M.Sh. et al. Reduction of
friction coefficient of ultrafine-grained CP titanium. Materials Science and
Engineering A, v. 371, p. 313-317, 2004.
[34] LA, P.Q., MA, J.Q., ZHU, Y.T. et al. Dry-sliding tribological properties of ultrafinegrained Ti prepared by severe plastic deformation, Acta Materialia, v. 53,
p. 5167-5713, 2005.
211
[35] MAY, J., HÖPPEL, H.W., GÖKEN, M. Strain rate sensitivity of ultrafine-grained
aluminium processed by severe plastic deformation, Scripta Materialia, v. 53,
p. 189-194, 2005.
[36] SEMIATIN, S.L., SALEM, A.A., SARAN, M.J. Models for severe plastic
deformation by equal-channel angular extrusion. Journal of Electronics Materials,
v. 56, p. 69-77, 2004.
[37] IWAHASHI, Y., WANG, W., NEMOTO, M. al. Principle of equal-channel angular
pressing for the processing of ultra-fine grained materials. Scripta Materialia, v. 35,
p. 143-146, 1996.
[38] ALKORTA, J., SEVILLANO, J.G. A comparison of FEM and upper-bound type
analysis of equal-channel angular pressing (ECAP). Journal of Materials Processing
Technology, v. 141, p. 313-318, 2003.
[39] PÉREZ, C.J.L. Upper bound analysis and FEM simulation of equal fillet radii angular
pressing. Modelling and Simulation in Materials Science and Engineering, v. 12,
p. 205-215, 2004.
[40] PÉREZ, C.J.L. On the correct selection of the channel die in ECAP processes.
Scripta Materialia, v. 50, p. 387-393, 2004.
[41] ALTAN, B.S., PURCEK, G., MISKIOGLU, I. An upper-bound analysis for equalchannel angular extrusion. Journal of Materials Processing Technology, v. 168,
p. 137-146, 2005.
[42] SHAN, A., MOON, I.G., KO, H.S. et al. Direct observation of shear deformation
during equal channel angular pressing of pure aluminum. Scripta Materialia, v. 41,
p. 353-357, 1999.
[43] EIVANI, A.R., TAHERI, A.K. An upper bound solution of ECAE process with outer
curved corner. Journal of Materials Processing Technology, v. 182, p. 555-563, 2007.
[44] EIVANI, A.R., TAHERI, A.K. The effect of dead metal zone formation on strain and
extrusion force during equal channel angular extrusion. Computational Materials
Science, v. 42, p. 14-20, 2008.
[45] PÉREZ, C.J.L., LURI, R. Study of the ECAE process by the upper bound method
considering the correct die design. Mechanics of Materials, v. 40, p. 617-628, 2008.
[46] SEGAL, V.M. Equal channel angular extrusion: from macromechanics to structure
formation. Materials Science and Engineering A, v. 271, p. 322-333, 1999.
212
[47] BEYERLEIN, I.J., TOMÉ, C.N. Analytical modeling of material flow in equal
channel angular extrusion (ECAE). Materials Science and Engineering A, v. 380,
p. 371-380, 2004.
[48] TÓTH, L., MASSION, R.A., GERMAIN, L. et al. Analysis of texture evolution in
equal channel angular extrusion of copper using a new flow field. Acta Materialia,
v. 52, p. 1885-1898, 2004.
[49] PRANGNELL, P.B., HARRIS, C., ROBERTS, S.M. Finite element modelling of
equal channel angular extrusion. Scripta Materialia, v. 37, p. 983-989, 1997.
[50] KIM, H.S., SEO, M.H., HONG, S.I. On the die corner gap formation in equal channel
angular pressing. Materials Science and Engineering A, v. 291, p. 86-90, 2000.
[51] KIM, H.S. Finite element analysis of deformation behaviour of metals during equal
channel multi-angular pressing. Materials Science and Engineering A, v. 328,
p. 317-323, 2002.
[52] SRINIVASAN, R. Computer simulation of the equichannel angular extrusion (ECAE)
process. Scripta Materialia, v. 44, p. 91-96, 2001.
[53] SUH, J.Y., KIM, H.S., PARK, J.W. et al. Finite element analysis of material flow in
equal channel angular pressing. Scripta Materialia, v. 44, p. 677-681, 2001.
[54] KIM, H.S. Finite element analysis of equal channel angular pressing using a round
corner die. Materials Science and Engineering A, v. 315, p. 122-128, 2001.
[55] DUMOULIN, S., ROVEN, H.J., WERENSKIOLD, J.C. et al. Finite element
modeling of equal channel angular pressing: effect of material properties, friction and
die geometry. Materials Science and Engineering A, v. 410-411, p. 248-251, 2005.
[56] SEMIATIN, S.L., DELO, D.P. Equal channel angular extrusion of difficult-to-work
alloys. Materials and Design, v. 21, p. 311-322, 2000.
[57] FIGUEIREDO, R.B., CETLIN, P.R., LANGDON, T.G. The processing of
difficult-to-work alloys by ECAP with an emphasis on magnesium alloys.
Acta Materialia, v. 55, p. 4769-4779, 2007.
[58] KIM, H.S. Evaluation of strain rate during equal-channel angular pressing. Journal of
Materials Research, v. 17, p. 172-179, 2002.
[59] KIM, H.S., SEO, M.H., HONG, S.I. Finite element analysis of equal channel angular
pressing of strain rate sensitive metals. Journal of Materials Processing Technology,
v. 130-131, p. 497-503, 2002.
213
[60] BAIK, S.C., ESTRIN, Y., KIM, H.S. et al. Dislocation density-based modeling of
deformation behavior of aluminium under equal channel angular pressing. Materials
Science and Engineering A, v. 351, p. 86-97, 2003.
[61] TÓTH, L.S., MOLINARI, A., ESTRIN, Y. Strain hardening at large strains as
predicted by dislocation based polycrystal plasticity model. Journal of Engineering
Materials and Technology, v. 124, p. 71-77, 2002.
[62] ESTRIN, Y., TÓTH, L.S., MOLINARI, A. et al. A dislocation-based model for all
hardening stages in large strain deformation. Acta Materialia, v. 46, p. 5509-5522,
1998.
[63] SUO, T., LI, Y., GUO, Y. et al. The simulation of deformation distribution during
ECAP using 3D finite element method. Materials Science and Engineering A, v. 432,
p. 269-274, 2006.
[64] SUO, T., LI, Y., DENG, Q. et al. Optimal pressing route for continued equal channel
angular pressing by finite element analysis. Materials Science and Engineering A,
v. 466, p. 166-171, 2007.
[65] SON, I.H., LEE, J.H., IM, Y.T. Finite element investigation of equal channel angular
extrusion with back pressure. Journal of Materials Processing Technology, v. 171,
p. 480-487, 2006.
[66] JIANG, H., FAN, Z., XIE, C. 3D finite element simulation of deformation behavior of
CP-Ti and working load during multi-pass equal channel angular extrusion. Materials
Science and Engineering A, v. 485, p. 409-414, 2008.
[67] CHEN, L.J., MA, C.Y., STOICA, G.M. et al. Mechanical behavior of a 6061 Al alloy
and an Al2O3/6061 Al composite after equal-channel angular processing. Materials
Science and Engineering A, v. 410-411, p. 472-475, 2005.
[68] MOREIRA, L.P., ROMÃO, E.C., FERRON, G. et al. Cyclic Bending and Stationary
Drawing Deformation of Metal Sheets: Experiments and Associated Numerical
Simulations. In: AIP Proceedings, 2005. v. 778, p. 667-672.
[69] NAGASEKHAR, A.V., TICK-HON, Y. Optimal tool angles for equal channel
angular extrusion of strain hardening materials by finite element analysis.
Computational Materials Science, v. 30, p. 489-495, 2004.
[70] AVITZUR, B. Metal Forming: Processes and Analysis. Mc Graw-Hill Publishing
Company Ltd., New Delhi. 1977, 500 p.
214
[71] KOBAYASHI, S., OH, S.I., ALTAN, T. Metal Forming and the Finite-Element
Method. Oxford University Press, New York. 1989, 377 p.
[72] PERIĆ, D., OWEN, D.R.J., HONNOR, M.E. A model for finite strain elastoplasticity
based on logarithmic strains: Computational issues. Computer Methods in Applied
Mechanics and Engineering, v. 94, p. 35-61, 1992.
[73] DRUCKER, D.C. Relation of experiments to mathematical theories of plasticity.
Journal of Applied Mechanics, v. 16, p. 349-357, 1949.
[74] BARLAT, F. Crystallographic texture, anisotropic yield surface and forming limits of
sheet metals. Materials Science and Engineering, v. 9, p.55-72, 1987.
[75] FERRON, G., MAKKOUK, R., MORREALE, J. A parametric description of
orthotropic plasticity in metal sheets. International Journal of Plasticity, v. 10,
p. 431-449, 1994.
[76] KHAN, A.S., HUANG, S. Continuum Theory of Plasticity. John Wiley & Sons,
New York. 1995, 421 p.
[77] MONTGOMERY, D.C., Design and Analysis of Experiments. John Wiley & Sons,
New York. 1997, 704 p.
[78] ROSOCHOWSKI, A., OLEJNIK, L. Numerical and physical modelling of plastic
deformation in 2-turn equal channel angular extrusion. Journal of Materials
Processing Technology, v. 125-126, p. 309-316, 2002.
[79] YOON, S.C., KIM, H.S. Finite element analysis of the effect of the inner corner angle
in equal channel angular pressing. Materials Science and Engineering A,
v. 490, p. 438-444, 2008.
[80] PAYDAR, M.H., REIHANIAN, M., EBRAHIMI, R. et al. An upper-bound approach
for equal channel angular extrusion with circular cross-section. Journal of Materials
Processing Technology, v. 198, p. 48-53, 2008.
[81] OH, S.J., KANG, S.B. Analysis of the billet deformation during equal channel angular
pressing. Materials Science and Engineering A, v. 343, p. 107-115, 2003.
[82] ORUGANTI, R.K., SUBRAMANIAN, J.S., MARTE, J.S. et al. Effect of friction,
backpressure and strain rate sensitivity on material flow during equal channel angular
extrusion. Materials Science and Engineering A, v. 406, p. 102-109, 2005.
[83] SON, I.H., JIN, Y.G., IM, Y.T. et al. Sensitivity of friction condition in finite element
investigations of equal channel angular extrusion. Materials Science and
Engineering A, v. 445-446, p. 676-685, 2007.
215
[84] YOON, S.C., QUANG, P., HONG, S.I. et al. Die design for homogeneous plastic
deformation during equal channel angular pressing. Journal of Materials Processing
Technology, v. 187-188, p. 46-50, 2007.
[85] MEDEIROS, N., LINS, J.F.C., MOREIRA, L.P. et al. The role of the friction during
the equal channel angular pressing of an IF-steel billet. Materials Science and
Engineering A, v. 489, p. 363-372, 2008.
[86] STOLYAROV, V.V., LAPOVOK, R. Effect of backpressure on structure and
properties of AA5083 alloy processed by ECAP. Journal of Alloys and Compounds,
v. 378, p. 233-236, 2004.
[87] JOHNSON, W., MAMALIS, A.G. Plasticity and Metal Forming. Helenic Steel
Publications. 1978, 85 p.
[88] MECKING,
H.,
KOCKS,
U.F.
Kinetics
of
flow
and
strain-hardening.
Acta Metallurgica, v. 29, p. 1865-1875, 1981.
[89] LURI, R., PÉREZ, C.J.L., LEÓN, J. A new configuration for equal channel angular
extrusion dies. Journal of Manufacturing Science and Engineering, v. 128,
p. 860-865, 2006.
[90] WAGONER, R.H., CHENOT, J.-L. Fundamentals of Metal Forming. John Wiley &
Sons, New York. 1997, 389 p.
216
9. ANEXOS
9.1 ANEXO 1: LISTA DE PUBLICAÇÕES
MEDEIROS, N., LINS, J.F.C., MOREIRA, L.P. et al. The role of the friction during the
equal channel angular pressing of an IF-steel billet. Materials Science and Engineering A,
v. 489, p. 363-372, 2008.
MEDEIROS, N., LINS, J.F.C., MOREIRA, L.P. et al. Theoretical and sensitivity analyses
for the equal channel angular extrusion process. Computational Materials Science
(em fase final de preparação).
MEDEIROS, N., LINS, J.F.C., MOREIRA, L.P. et al. Modelamento analítico da extrusão
em
canais
equiangulares.
Revista
Tecnologia
em
Metalurgia
e
Materiais
(aceito para publicação).
MEDEIROS, N., GARCEZ, R., MOREIRA, L.P. Soluções analíticas e previsões
numéricas para o processo de prensagem em canais equiangulares. In: 63º Congresso
Anual da ABM, 2008, Santos.
MEDEIROS, N., MOREIRA, L.P., LINS, J.F.C. et al. Análise de sensibilidade do processo
de prensagem em canais equiangulares. In: V Congresso Nacional de Engenharia
Mecânica, 2008, Salvador.
MEDEIROS, N., MOREIRA, L.P., LINS, J.F.C. et al. Análise dos efeitos de parâmetros
reológicos e tribológicos no processo de prensagem em canais equiangulares.
In: V Congresso Nacional de Engenharia Mecânica, 2008, Salvador.
MEDEIROS, N., MOREIRA, L.P., LINS, J.F.C. et al. Análise teórica do processo de
prensagem em canais equiangulares. In: 62º Congresso anual da ABM, 2007, Vitória.
MEDEIROS, N., MOREIRA, L.P., LINS, J.F.C. et al. Análise numérica de um aço IF após
um único passe de prensagem em canais equiangulares. In: 62º Congresso anual da ABM,
2007, Vitória.
217
MEDEIROS, N., MOREIRA, L.P. An upper bound solution for the equal-channel angular
pressing process. In: 19th International Congress on Mechanical Engineering, 2007,
Brasília.
MEDEIROS, N., MOREIRA, L.P., LINS, J.F.C. et al. A numerical and experimental
analysis of aluminium AA 1100 deformed by different ECAP routes. In: 19th Congress on
Mechanical Engineering, 2007, Brasília.
MEDEIROS, N., BAPTISTA, S.R., MOREIRA, L.P. et al. Computational simulation of an
if-steel deformed by equal channel angular pressing via the finite element method. In:
Solid Mechanics in Brazil, 2007. Anais do Solid Mechanics in Brazil, 2007. v. 1,
p. 309-320.